α-Fe和γ-Fe中氢扩散行为的第一性原理计算

张凤春， 张小山， 李春福， 文 平， 罗 强

(1.成都工业学院 材料工程学院， 成都 611730; 2.西南石油大学 材料科学与工程学院， 成都 610500; 3.西南石油大学 理学院， 成都 610500)

1 引 言

氢元素一直是极其敏感的元素，几乎对所有金属材料都存在不同程度的脆化倾向，并导致材料突然发生脆性断裂.例如，抗腐蚀性能优良的双相不锈钢[1-3]在恶劣的酸性腐蚀环境下也将发生失效断裂现象[4]，这引起了研究者们的广泛关注[5, 6].但目前为止，人们对于不锈钢中氢致裂纹的萌生与扩展机制认识尚不充分，特别是对于氢致开裂中裂纹产生的本质原因与扩展机制的微观解释更是未见报道.

乔利杰[7]等人研究表明，H原子能够扩散进入不锈钢，并在裂纹尖端、晶格缺陷等处聚集，从而控制裂纹的萌生、扩展以及传播.由此可以看出，氢致裂纹的萌生、扩展以及传播均与H原子的扩散过程息息相关，要想弄清钢材中裂纹产生的本质原因，首先则应充分认识与了解H原子在钢材中的扩散机制.随着量子化学和计算化学等学科的不断发展，不少科学家开始尝试借助理论方法与手段从微观层次开展相关研究[8-11].目前为止，关于H原子在金属Fe中扩散行为的理论研究已有不少报道.Jiang等人[9]采用密度泛函方法研究了H原子在α-Fe中四面体间隙位间的扩散行为，但并未详细阐述温度对扩散系数的影响作用.Sanchez等人[10]采用分子动力学方法模拟了H原子在α-Fe中的扩散行为，但并未涉及微观层次上H原子扩散行为的过渡态搜索.Ya等人[11]采用蒙特卡洛方法研究了H原子在α-Fe中的扩散行为，但并未将理论计算与实验手段相结合，对于钢材中腐蚀裂纹的萌生、扩展和传播等也未进行深入分析.

因此，本文从量子力学角度出发，计算了H原子在α-Fe和γ-Fe两相中的扩散激活能、扩散系数以及扩散过渡态，对比了H原子在两相中的扩散难易程度，从电子结构层次预测双相不锈钢中裂纹的萌生位置，分析裂纹产生的本质原因，同时结合双相不锈钢的氢致开裂实验，验证理论计算的可靠性，并深入探讨裂纹的萌生、扩展和传播过程，以期为抗酸性腐蚀双相不锈钢的设计提供理论依据，这对工程实际的腐蚀防护工作也具有极其重要的科研价值和现实意义.

2 计算模型与方法

2.1 计算模型

本文采用Materials Studio软件分别建立了α-Fe和γ-Fe晶体的晶胞结构.α-Fe晶胞属于四方晶系IM-3M空间群，体心立方结构，点阵参数a=b=c= 2.8664 Å，α=β=γ=90°[12]，如图1(a)所示.γ-Fe晶胞属于四方晶系FM-3M空间群，面心立方结构，点阵参数a=b=c= 3.5602 Å，α=β=γ= 90°[13]，如图2(a)所示.并利用超晶胞方法，分别建立了1×1×2的α-Fe和γ-Fe晶体的超晶胞模型，H原子在超晶胞中的间隙位置均存在四面体位(T)和八面体位(O)两种类型，分别如图1(b)、1(c)和2(b)、2(c)所示.

图1 α-Fe晶胞模型图(a)α-Fe原胞; (b) H在1×1×2 α-Fe四面体间隙位; (c) H在1×1×2 α-Fe八面体间隙位Fig.1 The structural model of α-Fe cell(a)α-Fe primitive cell; (b) H atom in the Tetrahedral site of 1×1×2 α-Fe; (c) H atom in the Octahedral site of 1×1×2 α-Fe

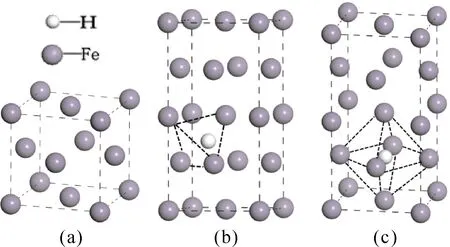
图2 γ-Fe晶胞模型图(a)γ-Fe原胞；(b) H在1×1×2 γ-Fe四面体间隙位；(c) H在1×1×2 γ-Fe八面体间隙位Fig.2 The structural model of γ-Fe cell(b)γ-Fe primitive cell; (b) H atom in the Tetrahedral site of 1×1×2 γ-Fe; (c) H atom in the Octahedral site of 1×1×2 γ-Fe

2.2 计算方法

本文所有计算均采用Materials Studio中的CASTEP模块完成[14, 15]，计算中电子波函数采用超软赝势[16]和平面波基组展开，电子交换关联势选用广义梯度近似(GGA)[17,18]下的RPBE泛函形式，平面波截断能选为450 eV，α-Fe和γ-Fe晶体结构优化的k点取样采用Monkhorst-Pack方法[19]，均选取为9×9×5.

3 计算结果与讨论

3.1 扩散激活能

已有研究表明[20]，H原子在α-Fe和γ-Fe晶胞中的最稳定间隙位置分别为四面体间隙(T)和八面体间隙(O).因此，H原子在α-Fe的T位间和γ-Fe的O位间优先发生扩散，分别称为TT扩散和OO扩散.为了分析H原子在α-Fe和γ-Fe中的扩散机制，本文采用Complete LST/QST方法分别搜索了H原子在α-Fe中TT扩散和γ-Fe中OO扩散的过渡态[21]，所得扩散势垒曲线分别如图3和图4所示.曲线中的能量最高点与最低点的差值即扩散势垒，也称为扩散激活能.曲线中能量的最高点即扩散的过渡态.

图3 α-Fe晶胞中H原子TT扩散势垒曲线Fig.3 The barrier curve of H atom diffusion in α-Fe along T→T

图4 γ-Fe晶胞中H原子OO扩散势垒曲线Fig.4 The barrier curve of H atom diffusion in γ-Fe along O→O

从图3、图4中可以看出，扩散过程中晶胞总能量先升高后降低，并且在扩散路径中点达到最大值.同时，H原子在α-Fe晶胞中TT扩散和γ-Fe中OO扩散所需的扩散激活能分别为0.2007 eV和1.1910 eV.两者对比不难看出，α-Fe中TT扩散的扩散激活能更低，这说明H原子在α-Fe中TT扩散更为容易.

3.2 扩散系数

1989年，物理化学家阿伦尼乌斯提出了著名的阿伦尼乌斯公式，该公式不仅反映了化学反应的速率常数与温度间的关系，同时也能用于表示扩散系数与温度间的关系[22-24]，扩散系数的表达式如下所示：

(1)

其中，D为扩散系数；D0为扩散指前因子；Ea为扩散激活能；kB为玻尔兹曼常数，约为1.3806 × 10-23J/K；T为绝对温度.

而根据过渡态理论，扩散系数与跃迁频率存在函数关系，并且跃迁频率满足阿伦尼乌斯公式[24-26]，其表达式如下[27]：

D=L2×Γ

(2)

其中，D为扩散系数；L为跃迁距离；Γ为跃迁频率.

1949年，Wert等人[28, 29]建立了杂质原子在固体中扩散的跃迁频率表达式：

(3)

式中，ν0为杂质原子的有效跃迁频率或震动频率，其表示原子在单位时间内尝试跃迁的次数.

因此，将(3)式代入(2)式可得由原子跃迁频率所表示的扩散系数表达式：

(4)

又因玻尔兹曼常数kB=R/NA，将其代入(4)中，可得：

(5)

其中，NA为阿伏伽德罗常数，约为6.0221 × 1023mol-1；R为理想气体常数，约为8.3141 J·mol-1·K-1.式(5)即扩散系数与温度的关系式，而固体中杂质原子的有效跃迁频率或震动频率一般处在1013Hz数量级[30]，因此本文中H原子的有效跃迁频率v0选取为1013Hz；另外，α-Fe晶胞中TT扩散的Ea约为0.2007 eV，跃迁距离L约为1.3280 Å；而γ-Fe晶胞中OO扩散的Ea约为1.1910 eV，跃迁距离L约为2.5872 Å.将以上数据一并代入到(5)式中，可分别得到H原子在α-Fe中TT扩散和在γ-Fe晶胞中OO扩散的扩散系数与温度的表达关系式：

(6)

(7)

从式(6)和式(7)中可以看出，H原子在α-Fe晶胞中TT扩散的扩散激活能为19.3645 kJ/mol，而在γ-Fe晶胞中OO扩散的扩散激活能约为114.9132 kJ/mol，二者对比不难发现，H原子在α-Fe晶胞中扩散所需激活能较低，扩散过程较为容易，而H原子在γ-Fe晶胞中扩散所需激活能较高，扩散过程较为困难.因此，我们认为在同等环境条件下，H原子在α-Fe中较为活跃，将容易在晶格缺陷处聚集，甚至造成氢致开裂等严重后果，而在γ-Fe中由于扩散困难，在一定程度上能够阻碍H原子在缺陷处聚集，这对于氢脆效应的减弱是较为有益的.

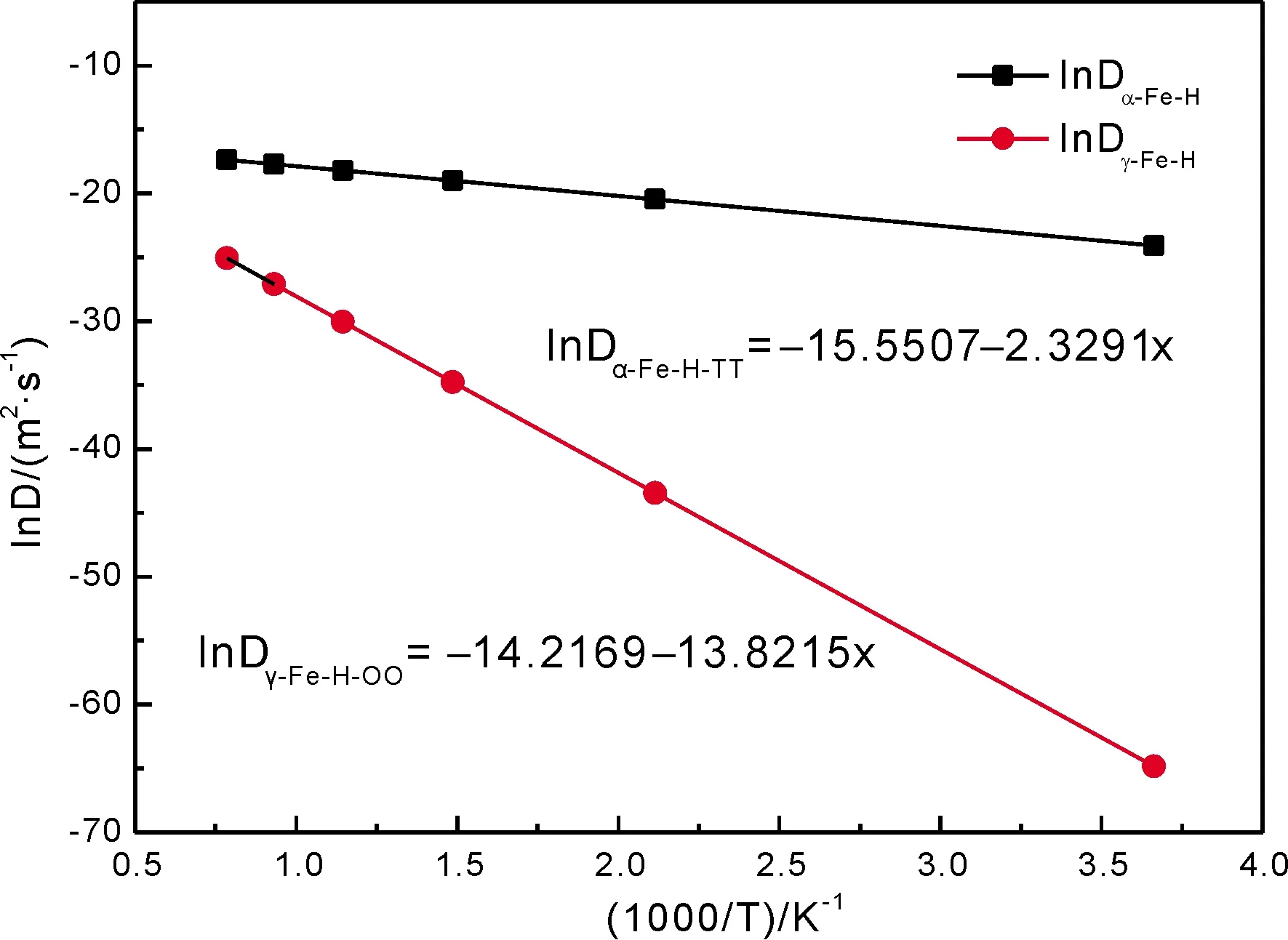
图5 H原子在α-Fe和γ-Fe中扩散系数对数与温度倒数关系的阿伦尼乌斯图Fig.5 Thearrhenius plot between the logarithm of diffusion coefficient and the reciprocal of temperature for H atom diffusion in α-Fe and γ-Fe

为了更为直观地分析温度对扩散系数的影响作用，并且对比H原子在α-Fe和γ-Fe晶胞中的扩散行为，本文分别计算了273 K ～ 1273 K温度范围内，H原子在α-Fe和γ-Fe晶胞中的扩散系数对数与温度倒数关系的阿伦尼乌斯图，如图5所示.从图中可以看出，与γ-Fe晶胞相比，H原子在α-Fe晶胞中的扩散系数更高一些，这是因为H原子在α-Fe晶胞中的扩散激活能比γ-Fe晶胞低的多，其所需克服的能量势垒较低，扩散较为容易.不过随着温度的升高，二者之间的差距逐渐减小，这可能是由于温度升高后，原子的晶格振动更为激烈，H原子跃过能量势垒的概率增大，从而扩散系数也呈增大趋势.

3.3 2205双相不锈钢的氢致开裂(HIC)实验

为了验证计算结果的可靠性，本文根据GB/T8650-2006管线钢和压力容器钢氢致开裂评定方法对2205双相不锈钢进行了氢致开裂(HIC)实验[31]，并结合金相分析方法，将HIC试验后的试样在Murukanmi溶液(30KOH+ 30gK3Fe(CN)6+100mLH2O)中进行化学侵蚀，温度85 ℃左右，时间3～5 min，侵蚀后迅速用清水冲洗干净，冷风吹干后在XJG-05型光学显微镜下观察裂纹分布情况，如图6所示.

图 6 2205双相不锈钢HIC测试裂纹金相图Fig.6 The metallographic figure for HIC crack of 2205 duplex stainless steel

从图6中可以看出，HIC裂纹在铁素体相中呈穿晶型开裂；当裂纹发展至铁素体奥氏体相界面时，裂纹则“避开”了奥氏体相而沿两相的相界面发展，呈间晶型开裂.可以看出，2205双相不锈钢应力腐蚀破裂形态包含穿晶型开裂和间晶型开裂两种，属于混合型开裂方式，并且裂纹优先在铁素体相中发展，这也证明了本文计算结果的可靠性.因此，在同等环境条件下，由于H原子在铁素体相中扩散激活能较低，表现得较为活跃，其容易在晶格缺陷处聚集，从而造成裂纹易于在该相中萌生和扩展.而当裂纹扩展至两相界面时，由于H原子在奥氏体相中扩散较为困难，其“容纳”H原子的能力非常强，H原子将不足以对奥氏体相造成破坏，其在一定程度上能够阻碍裂纹的进一步发展，从而使裂纹沿两相界面发展.故铁素体相是双相不锈钢中的“弱相”，是裂纹优先发展的区域，这为抗H2S应力腐蚀双相不锈钢的设计提供了重要的理论依据.

4 结 论

本文采用基于密度泛函理论的第一性原理方法，研究了H原子在α-Fe和γ-Fe晶胞中的扩散行为，计算了H原子在两相中的扩散系数，并结合2205双相不锈钢的HIC实验，分析了氢致裂纹的萌生位置和扩展机理，主要得到了以下结论：

(1)H原子在α-Fe中TT扩散的能量势垒为0.2007 eV，过渡态结构为H原子处于八面体间隙位.H原子在γ-Fe中OO扩散的能量势垒为1.1910 eV，过渡态结构为H原子位于两个面心Fe原子的中心位置处；

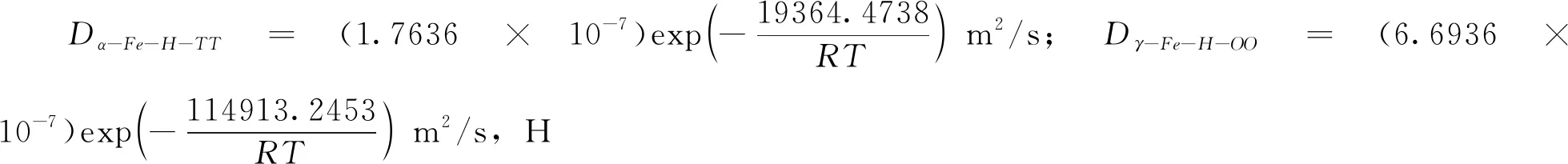
(3)2205双相不锈钢氢致开裂实验表明：氢致裂纹在铁素体相中呈穿晶开裂，而在传播过程中受到了奥氏体相的阻碍，使得裂纹沿两相界面发展，说明铁素体相是2205双相不锈钢中的“弱相”，是氢致裂纹的初始萌生位置，这同时证明了本文第一性原理计算的可靠性.