稀有气体二聚体基准集NgD×15构建及其对DFT方法的评价

王裕平, 魏孝珍，王一波

(贵州大学化学系 贵州省高性能计算化学重点实验室, 贵阳 550025)

1 引 言

目前在分子间相互作用领域，用于训练和评价各种近似理论方法的基准集主要有Hobza研究组发展的A24[1]，S22[2]，S22×5[3]，S66，S66×8[4]以及X40，X40×10[5]等，这些基准集未包含稀有气体二聚体；Grimme研究组发展了GMTKN24[6]，GMTKN30[7]，GMTKN55[8]等基准集数据库，其中GMTKN30仅给出了Ne2至 Rn2平衡位置数据，未给出势能曲线；Head Gordon在MGCD84数据库的RG10基准集中仍沿用了Tang-Toennies经验势[9].

1998年Partridge等用CCSD(T)方法计算了He2解离能，同时考察键函数的作用[10].其后Hellmann，Sheng等计算并拟合了Ne2[11]，Ar2[12]，Kr2[13]，Xe2[14]和Rn2[15]的势能曲线.但是由于这些研究结果所采用的方法、基函数不一致，难以构成一套完整、系统和精确的基准集.以至于2017年Kovacs等评测13种DFT-D3方法时，是以自己的CCSD(T) /aug-cc-pVTZ计算结果为评测标准[16]，Austin 等在发展APF-PFD方法时也是采用类似的做法[17].以CCSD(T) /aug-cc-pVTZ结果作为标准，基函数还远远没有收敛，对DFT方法的评价不严谨.作者在发展B972-PFD[18]DFT方法时也是缺乏可靠的Ng2参考基准.因此建立完整、精确的Ng2基准集非常必要.

根据前人的大量计算实践，在基函数极限下用CCSD(T)计算结果构建Ng2体系相互作用势是合适的，但该体系作用势很小，对基函数非常依赖，且收敛很慢，关键在于使用收敛的基函数.中点键函数能够有效地加速基函数收敛，本文用aug-cc-pV5Z核中心基，加上陶福明等所推荐的中点键函数[19, 20]，仔细考察了键函数的影响，精确地给出Ng2体系的势能曲线，建立了一个较为准确、完整的Ng2基准集，并重新测试、评价了目前常用的DFT色散及非局域校正方法.

2 NgD×15基准集的构建

本文所建立的NgD×15基准集，对He2，Ne2，Ar2，Kr2，Xe2和Rn2每个体系各取15个测试点，共计90个点.我们确定核间距时，以平衡核间距Re×0.9为起始点，以0.2 Å或0.3 Å及以上的间距作为步长取点，核间距具体数值见表2.

3 研究方法

首先在CCSD(T)[21]计算水平下，以He2为例分别使用aug-cc-pVXZ(X=T, Q, 5, 6)以及d-aug-cc-pVXZ(X=7, 8)基组，并在aug-cc-pV5Z基组下分别加上{6s6p6d3f2g1h}，{6s6p6d3f2g2h}，{6s6p6d6f3g2h1i}以及{6s6p6d6f3g3h2i1k}等高角量子数键函数集(以下分别标记为BF1-BF4)，研究相互作用势对基函数的收敛性.所有计算均使用Boys和Bernard[22]所提出的均衡校正法(Counterpoise Procedure, CP) 消除BSSE.

以CCSD(T)/ aug-cc-pV5Z-{6s6p6d3f2g1h}方法建立基准集后；对B97M-V[23]，ωB97M-V[24]，ωB97X-V[25]，B97M-rV，ωB97X-rV，ωB97M-rV[26]，ωB97M(2)[27]等7种DFT-NL方法以及Kovacs等所测试的DFT-D3方法[16]，在def2- QZVPPD基组，(250, 974)积分网格下进行了测试，并统计分析了各种方法的误差.

全部研究工作采用Gaussian16 RevA.03[28]、Q-Chem5.1[29]程序，在贵州大学云计算平台上完成计算.

4 结果与讨论

4.1 NgD×15基准集

图1是以He2体系为例的计算结果.由图1可知：CCSD(T)/d-aug-cc-pV7Z计算水平下，He2的势能曲线计算没有得到收敛；直到d-aug-cc-pV8Z，He2势能曲线才接近收敛.比较CCSD(T)/aug-cc-pV5Z- BF1的计算结果发现，此时的计算精度已经达到CCSD(T)/d-aug-cc-pV8Z水平；当键函数再进一步增大到{6s6p6d6f3g3h2i1k}时，其势能面的最低点并无明显的变化，最大误差只有0.015cm-1.因此，CCSD(T)/aug-cc-pV5Z- BF1已趋于收敛.

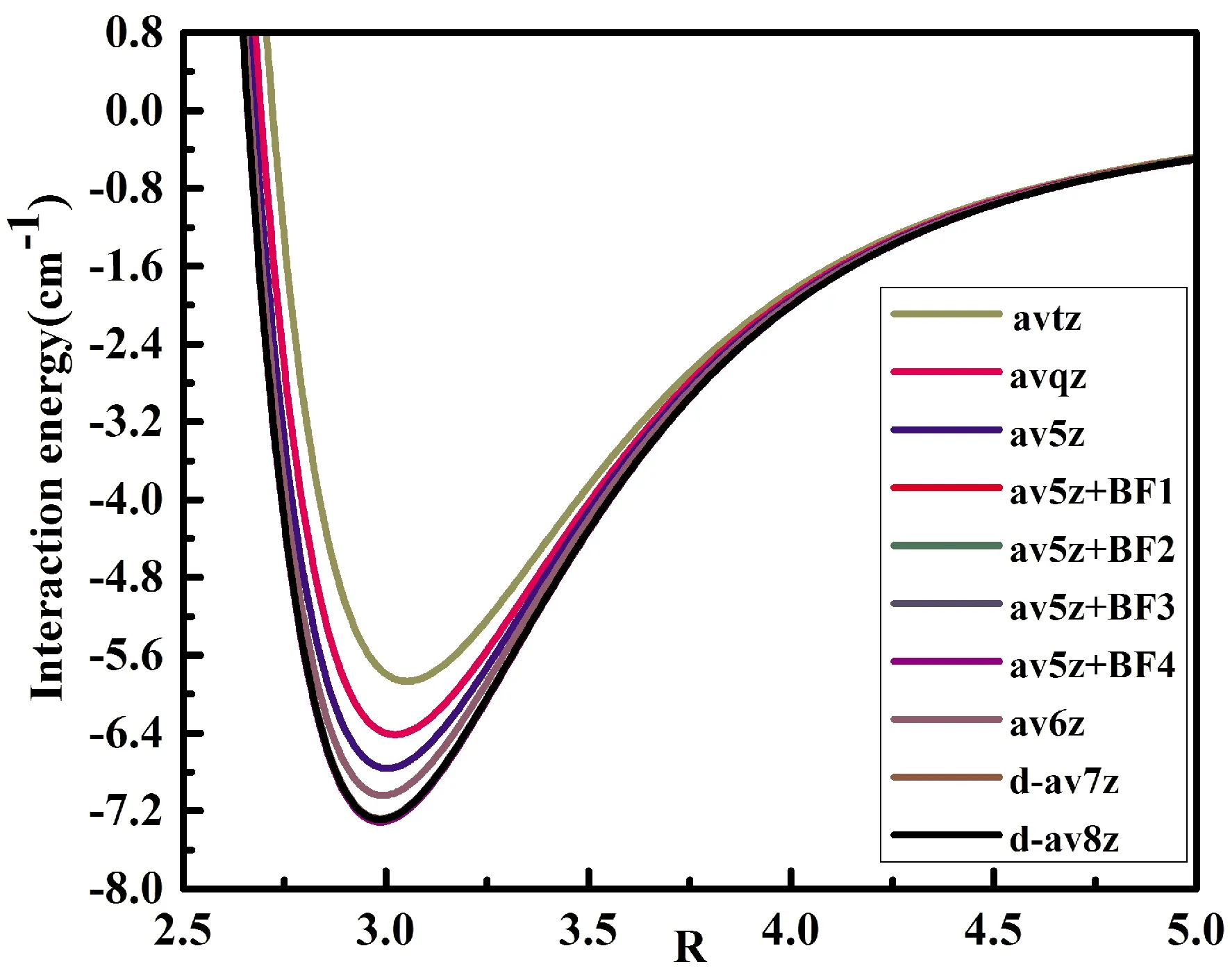
图1 CCSD(T)方法在aug-cc-pVXZ(X=5, 6)，d-aug-cc-pV XZ(X=7, 8)以及 aug-cc-pV5Z-BF(1-4)基组下对He2势能面的计算结果.Fig.1 The results of potential energy surface calculated for the He2 at the CCSD(T)/ aug-cc-pVXZ(X=5, 6)，CCSD(T)/ d-aug-cc-pVXZ(X=7, 8) and CCSD(T)/ aug-cc-pV5Z-BF(1-4) levels.

我们继续在CCSD(T)/ aug-cc-pV5Z- BF1水平计算了Ne2至Rn2体系，并且与aug-cc-pVXZ(X=T, Q, 5)基组结果进行了对比.

表2为CCSD(T)/ aug-cc-pV5Z-BF1计算水平下，所有同核Ng2体系的相互作用势在不同核间距下的具体数值.我们发现Head-Gordon等所使用的Tang-Toennies经验势结果与NgD×15计算结果相一致.对于He2体系误差只有0.1 cm-1，绝对误差最大的Kr2，也只有5.5 cm-1，说明稀有气体的Tang-Toennies经验势模型是可信的.

表1 NgD×15的平衡核间距(Å)与解离能(cm-1)文献参考值与本次研究相关的计算数值

Table 1 Literature values and calculated values of this study for the equilibrium internuclear distancesR(Å) and dissociation energiesΔE(cm-1) of NgD×15

DimerRefThis workRΔERΔEHe22.980[10]7.4502.9767.430Ne23.10[11]28.753.10628.74Ar23.80[12]97.273.79097.31Kr24.0[13]134.44.067134.8Xe24.4[14]192.24.392194.9Rn24.483245.4

Ref[10-14]为分别在CCSD(T)/aug-cc-pVTZ-{6s6p6d3f3g3h}，CCSD(T)/t-aug-cc-pV6Z-{4s4p3d3f2g}，CCSD(T)/d-aug-cc-pV6dZ-{4s4p3d3f2g}，CCSD(T)/t-aug-cc-pV6Z-{4s4p3d3f2g}，CCSD(T)/d-aug-cc-pV6Z-{4s4p3d3f2g}计算水平下的结果；this work为CCSD(T)/ aug-cc-pV5Z- BF1的计算结果.

表2 NgD×15核间距(Å)与对应的相互作用势(cm-1)

4.2 DFT-D3和DFT-NL方法的评价

以下表3是以表2数据为基准集，对DFT-NL以及DFT-D3等方法计算结果的绝对均方根误差RMSD以及相对均方根误差RMSRD的具体数值.

由表3可知，在Kovacs等人的测试结果中表现较好的B3LYP-D3(BJ)，CAM-B3LYP-D3，B3PW91-D3，PBE0-D3以及B97-D3等方法在此测试中与标准参考值的总体误差相对还是比较大的；尤其是对于He2体系的计算，绝对均方根误差RMSD数值在4-22 cm-1之间；PBE-D3，TPSS-D3泛函，其绝对均方根误差RMSD已经超出15 cm-1.DFT-NL方法中表现较好的ωB97X-V以及ωB97X-rV方法对He2体系计算的绝对误差虽然只有0.9 cm-1左右，但是相对误差RMSRD依然较大.所以对于He2这种极弱的相互作用体系，DFT-D3以及DFT-NL均不能提供较好的描述.从He2至Rn2绝对误差增大，而Rn2的绝对误差大都在20-60 cm-1以上；在这些DFT-NL方法中，除了B97M-V以及ωB97M-V，ωB97M(2)方法的误差略大，其余的均在25cm-1之间，DFT-NL方法相对于DFT-D3优势明显，特别是ωB97X-V，ωB97X-rV两种DFT-NL方法.

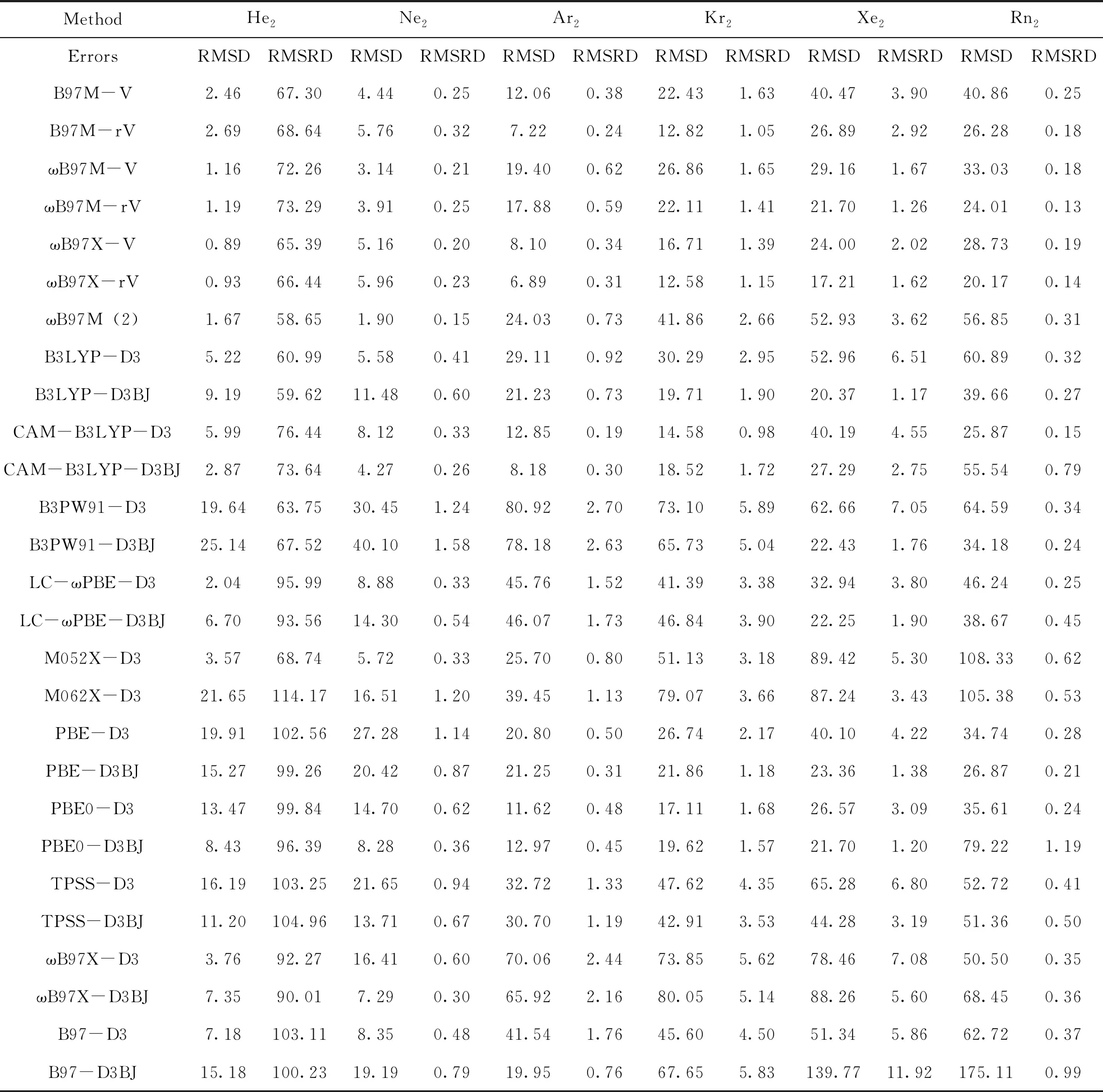
表3 DFT-NL以及DFT-D3(BJ)等方法的测试误差分析结果(cm-1)

5 结 论

本文在CCSD(T)/aug-cc-pV5Z-{6s6p6d3f2g1h}水平下，经BSSE均衡校正后，获得了He2至Rn2全部同核稀有气体二聚体的15点相互作用势，构建了NgD×15基准集.并以此为标准重新评价了DFT-D3和DFT-NL方法对色散作用的描述，发现DFT-NL总体上要强于DFT-D3方法.Kovacs等的测试结果中表现最好的B3LYP-D3， B3PW91-D3，PBE0-D3以及B97-D3等方法绝对均方根误差RMSD相对于DFT-NL方法较大.在所有的DFT-NL方法中，ωB97X-V及ωB97X-rV两种方法是该体系最优性价比的方法.