icMRCI方法研究NS±离子体系基态光谱

王兴炜， 宋晓书， 李思桦

(贵州师范大学物理与电子科学学院， 贵阳 550025)

1 引 言

S元素和N元素是化学、生物中重要的组成元素,他们形成的NS分子也广泛存在于化学反应过程、燃烧过程，以及星际空间之中.一直是在实验室光谱测定以及星际观测中备受关注的分子，NS分子及其正离子NS+都已经被证明存在于星际空间中[1]，这一发现引起了理论物理学家和天文学家对NS和NS±体系的广泛兴趣，因此对NS±离子进行精确的光谱测量和高精度的电子结构从头计算研究，已经成为分子物理领域中的研究热点.

对NS+体系的研究早在1977年Dyke[2]等人就通过电子光谱研究了NS+(X1Σ+)基态的电离能,1979年Huber和Herzberg[3]又对NS+(X1Σ+)的光谱常数进行了实验研究，1997年Gerbaux[4]等对NS+进行了光谱分析研究，遗憾的是他们并没有给出NS+的光谱常数.1992年Parsons和Passmore[5]实验研究了NS+基态的离解能，得到离解能为476 kJ/mol.在理论研究方面,最早由O`Hare[6]在1970年利用Hartree-Fock-Roothaan方法计算了NS+(X1Σ+)离解能D，1974年Török[7]通过理论计算得出了NS+(X1Σ+)的平衡核间距Re，1978年Karpfen[8]利用从头计算方法结合高斯基组计算了NS+(X1Σ+)的平衡核间距以及平衡态能量.1986年Karna和Grein[9]利用多参考组态方法和双zeta基组计算了NS+基态和激发态的势能函数以及光谱常数,Peter和Woods[10,11]分别在1988年和1990年计算了NS+(X1Σ+)的势能函数和光谱常数.在2004年Czernek和Zivny[12]采用耦合簇理论CCSD (T)计算了NS+(X1Σ+)的势能函数和光谱常数，2009年Yaghlane和Hochlaf[13]采用aug-cc-pV5Z基组结合完全活性空间自洽场(CASSCF)和内收缩多参考组态相互作用方法计算了NS+多个态的势能函数和光谱常数.

相比NS+而言对NS-体系的研究相对较少，实验方面1982年Burnett等[14]人对NS-进行了光电谱的实验探测，并通过获得的实验谱线推出了NS-体系的Re和ωe，在理论研究方面，Bruna和Grain[15]在实验基础上采用MRD-CI方法结合添加了弥散函数和极化函数的DZP基组计算得到了NS-体系的部分光谱常数，2004年Czernek[16]等人用CCSD(T)/cc-pVQZ方法得到了体系相应的光谱常数，此外还通过基组外推方法得到了体系的离解能，2013年Li Song[17]等人采用单双迭代包括三重激发的耦合簇方法CCSD(T)结合系列相关一致基组aug-cc-pVXZ(X=D,T,Q,5)，通过最小二乘法拟合方法确定了NS-体系的解析势能函数，并计算得到了一系列光谱常数.不过以上研究大多集中在NS±体系的势能函数和分子光谱研究，关于NS±体系基态的振转能级和离心畸变常数的报道却并未见到.

已有研究结果表明多参考组态相互作用的计算方法可以有效提高计算精度[18-20],因此本文采用包含Davidson修正的内收缩多参考组态相互作用(icMRCI+Q)的方法对NS+(X1Σ+)基态和NS-(X3Σ-)基态的势能函数和振转能级进行研究.利用从头计算方法(ab initio)计算得出了NS±的基态势能曲线，通过求解原子核相关的一维Schrödinger方程得到基态光谱常数、振动能级G(v)和离心畸变常数Bv、Dv，为这一体系的进一步研究提供参考.

2 计算方法

本文中所有涉及到电子结构相关计算均在Molpro 2018[21]程序包中进行.光谱常数的计算则是通过求解原子核相关的Schrödinger方程的Level8.0[22]程序计算得到.由于Molpro程序的限制，在计算时只能把分子对称性降低到C2v群，在C2v点群中有4个不可约表示即A1,B1,B2,和A2，由群论知识可得如下关系；Σ+=A1,∏=B1+B2,Δ=A1+A2以及Σ-=A2,为了获得NS±离子基态的势能函数我们分别尝试采用了不同的基组Dunning关联一致基组做结构优化包括aug-cc-pV5Z以及Peterson等人用于显关联计算得F-12基组cc-pVQZ-F12,势能函数的计算是在0.9 — 4.5 Å的核间距内对NS±离子体系进行单点能计算.在对NS±体系计算过程中主要分为三步，首先采用自旋限制的Hartree-Forck(RHF)方法分别得到NS+(X1Σ+)基态和NS-(X3Σ+)基态的波函数，然后以此波函数为基础采用完全活性空间自洽场(CASSCF)方法进行轨道优化,最后利用完全活性空间自洽场方法优化得到的波函数作为参考态进行包含Davison修正内收缩多参考组态相互作用(icMRCI+Q)计算,在CASSCF方法和icMRCI方法计算过程中将8个分子轨道(4,2,2,0)作为活性空间，这些轨道对应S原子3s3p和N原子2s2p壳层的所有原子轨道，将S原子的1s2s2p壳层和N原子的1s壳层的电子放入芯轨道.获得体系势能曲线后, 通过求如下式(1)核相关径向Schrödinger方程获得分子体系的光谱常数、振动能级和离心畸变常数.

(1)

其中μ为体系原子的约化质量，ν为振动量子数J为转动量子数,Eν,J为振转能级，Eν,J可以表示为如下形式(2)

Eν,J=G(ν)+Bν[J(J+1)]-

Dν[J(J+1)]2+…

(2)

G(ν)为振动能级,Bν,DV为不同阶次的离心畸变常数.

3 结果与讨论

3.1 势能曲线与光谱常数

利用icMRCI+Q方法，计算了NS+(X1Σ+)和NS-(X3Σ-)体系的势能曲线，根据分子反应静力学基本原理结合群论可以推出NS-(X3Σ-)的离解极限对应为S-(2Pu)+N(4Su)，同理可以推出NS+(X1Σ+)的离解极限为N(4Su)+S+(4Su)，为了能够直观理解将计算得到的NS±基态势能曲线画在图1.

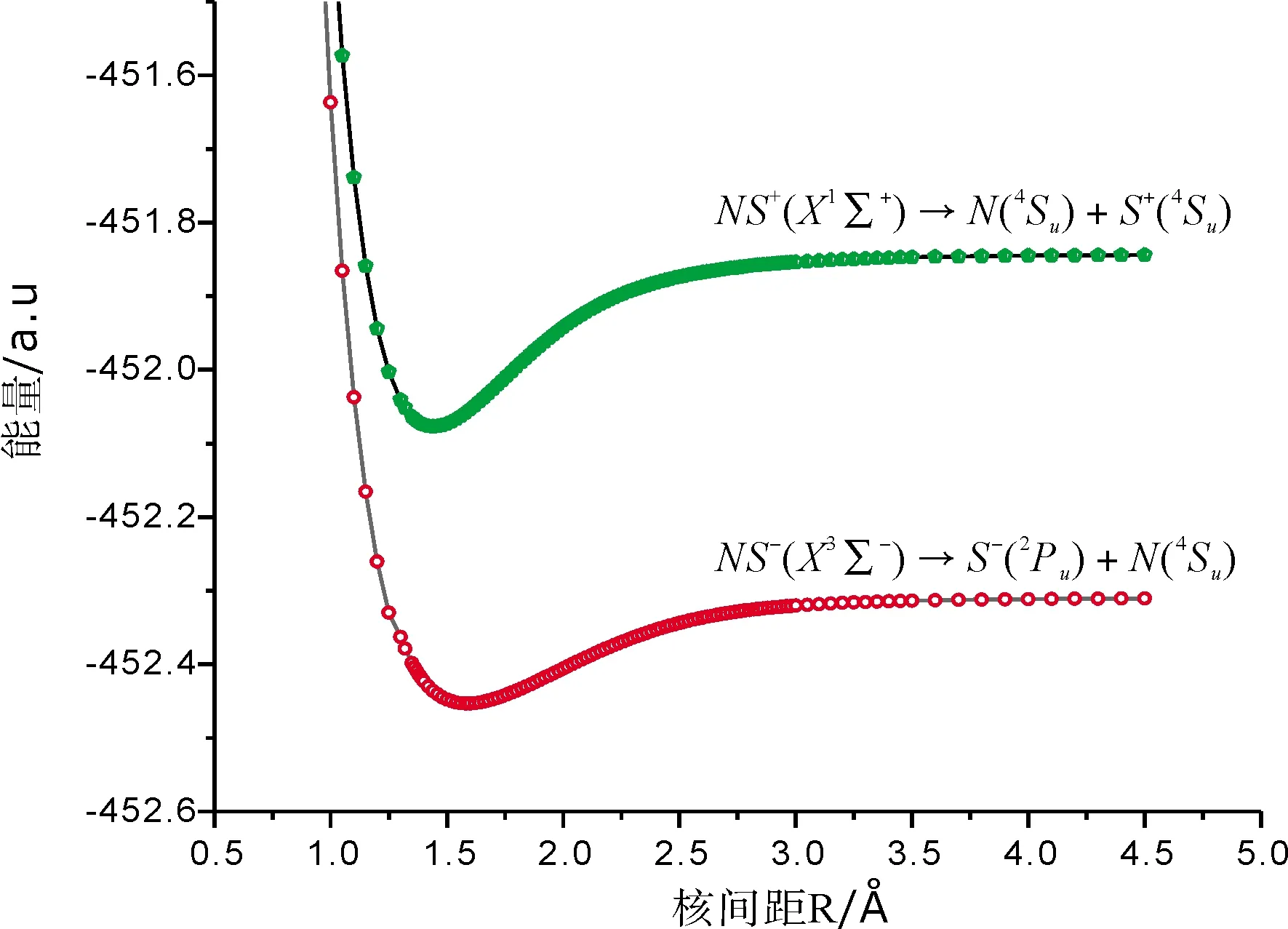
图1 NS±离子基态势能曲线Fig.1 Potential energy curves of ground states for ions

通过将aug-cc-pV5Z和aug-cc-pVQZ-F12基组水平下获得的势能曲线带入Level8.0程序包分别计算得到了NS+(X1Σ+)基态和NS-(X3Σ-)基态的光谱数据，其中包括平衡核间距Re、谐振频率ωe、非谐振常数ωeχe、平衡转动常数Be、振转耦合常数αe和离解能De.并将两个体系基态的光谱常数分别列入表1和表2；为了方便与本文计算结果进行比较，将实验值和其他可获得的理论值也列入表中.从表1中可以看出两种不同基组水平下所计算得到的NS+(X1Σ+)基态光谱数据没有太大的差别，但是对比发现借助aug-cc-pV5Z(AV5Z)基组所得的计算结果Re和ωe比现有的文献值更为接近实验值[3]，本文的平衡核间距与实验值的相对误差δRe=0.069%，即便是与实验值最为接近的文献[13]所得结果也和本文的计算结果是一致的.与此同时本文得到的谐振频率与实验值的相对误差δωe也只有0.024%，同样与实验值最为接近的文献[13]相对误差δ‘ωe=0.67%比我们得到的计算结果与实验值的相对误差要大，虽然本文计算得到的非谐振常数ωeχe与实验数据有所偏离但是因为ωeχe实验数据的标准偏差较大因此本文的计算结果的精度较之文献[13,14]中的计算精度是有所提高的.

表 1 NS+(X1Σ+)基态光谱数据

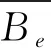
3.2 振动能级和光谱常数

利用Level程序对采用icMRCI+Q方法计算获得的NS+(X1Σ+)基态和NS-(X3Σ-)基态势能

表2 NS-(X3Σ-)基态光谱数据

曲线进行拟合计算，得到了当转动量子数J=0时这两个离子体系基态所有的振动能级和与之相对应的转动常数Bν和六个离心畸变常数，但是由于篇幅限制而略去了两个离子体系的高阶离心常数Lν、Mν、Nν和Oν,只将NS+(X1Σ+)和NS-(X3Σ-)体系的前30个振动能级的G(ν)、Bν和Dν分别列于表3.目前关于NS±体系基态振动能级和分子离心畸变常数的报道并不多见，所以我们计算得到的NS±体系基态的振动能级和离心畸变常数有助于该体系的进一步实验研究以及在星际分子检测方面作为理论参考.

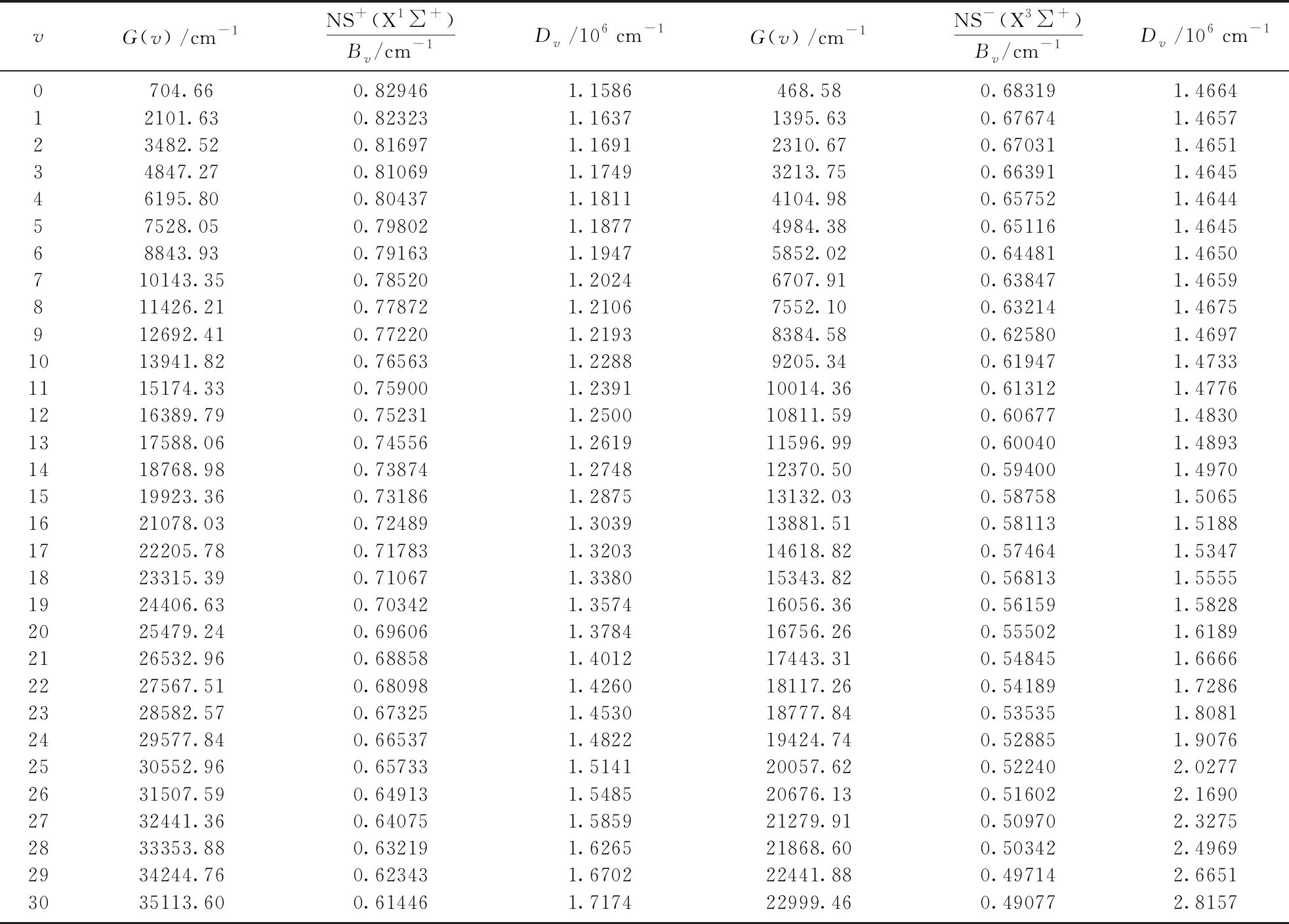
表3 NS±分子离子基态的振动能级和离心畸变常数(J=0)

4 总 结

本文利用高精度的内收缩多参考组态相互作用包含Davison能量修正(icMRCI+Q)的方法结合相关一致基组aug-cc-pV5Z和显关联计算的F-12基组cc-pVQZ-F12，分别计算得到了NS+(X1Σ+)基态和NS-(X3Σ-)基态的势能曲线,分析发现基于pV5Z基组水平下计算的势能曲线获得的光谱数据与NS±体系已有的实验数据吻合得很好，因此可以有理由相信本文的计算已经达到了较高精度，进而计算了该体系振动能级和当转动量子数J=0时的分子离心畸变常数，为今后在NS±体系尤其是在光谱信息相对缺乏的NS-阴离子体系提供进一步实验以及天体物理检测等方面的研究作为参考.