培养高阶思维 促进深度学习——例谈数学运算课高阶思维培养策略

夏建华

（威海市第二实验小学，山东 威海 264500）

数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程。主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法、设计运算程序，求得运算结果等。在数学运算核心素养的形成过程中，教师应引领学生进一步发展数学运算能力，能有效借助运算方法解决实际问题；能够通过运算促进数学思维发展，养成程序化思考问题的习惯；形成一丝不苟、严谨求实的科学精神。

传统的课堂教学，不注重引领学生充分经历知识的形成过程，简单将算法告之学生，再加以练习巩固，这种教学行为带来的学习效果往往是学生只从表面上掌握了计算技能，但为什么要这样算，却说不清道不明，把算理教学教成了低阶思维的记忆层次，不利于学生高阶思维的发展。怎样让学生自主探究算理、归纳算法，乐于运算也学有价值，是我对本节课的目标追求与实践思考。

一、类比迁移，整体架构，培养思维的深刻性

思维的深刻性，是指思维活动的抽象程度和逻辑水平，以及思维活动的广度、深度和难度。它既表现在严密的思维活动过程之中，又表现在思维活动结果的广度和深度之上，并能经受实践的检验，达到举一反三、触类旁通的效果。

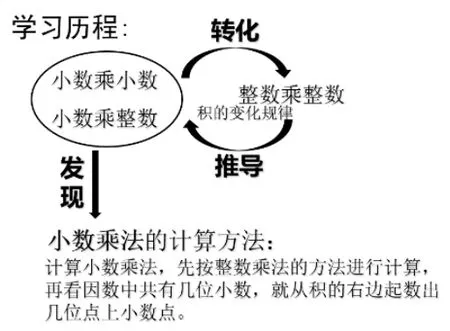
在温故环节中，我重点引领学生复习两方面的知识（如图）：一是复习三年级时学过的积的变化规律。通过两组口算，寻找因数和积的变化规律，为后面学习小数乘小数时需观察两个因数的变化引起积的变化做好铺垫；二是复习上节课学过的小数乘整数。通过笔算说算理“你是怎么算的？为什么这样算？”让学生知其所以然，为后面学习小数乘小数时寻找最近的生长点，将小数乘整数的方法迁移到小数乘小数中。

在新授环节，我以学生感兴趣的购物场景进行导学：橙子13.9元/kg，西红柿7.88元/kg，小兰买0.9千克的橙子和1.5千克的西红柿各花了多少钱？在解决两个问题中，学生分别列出算式13.9×0.9和7.88×1.5，并观察这两道乘法算式与之前学过的乘法算式有什么区别？学生通过回顾、对比，发现这两道算式都是小数乘小数，而之前学过的是整数乘整数、小数乘整数，这是本课中学生第一次认识“小数乘小数”。而后，学生凭借自己的经验，自主尝试进行小数乘小数的两道竖式计算。在交流、辨析中，发现小数乘小数与小数乘整数的计算既有共性，也有不同。共性之处在于它们都是把小数乘法转化为整数乘法算出乘积后，再根据因数和积的变化规律确定积中的小数点的位置。不同之处在于：一是小数乘小数不像小数乘整数只关注一个因数的变化，而要同时关注两个因数的变化；二是小数乘小数不像小数乘整数乘积比它本身大，而有可能会出现乘积比它本身还小的情况。在对比中，引导学生合理进行迁移，同时凸显小数乘小数的本质特征，这是本课中学生第二次认识“小数乘小数”。接着我又呈现了一组直接说结果的计算练习（如图），让学生在短时间内根据相应的整数积，快速说出“小数乘小数的积”，学生认识水平越来越高，最后一组抛开具体的数只有抽象的符号表达式，学生也能慧眼识别，探究的氛围迅速升到了最高点，整个课堂的学习气氛达到了炽热化。此时，学生对小数乘小数的理解真可谓“拨开云雾见月明”，这是本课中学生第三次认识“小数乘小数”。

总结环节中，先请学生自主归纳小数乘小数的计算方法，并引领学生思考这种方法是否适合于之前学过的小数乘整数，接着抛出问题：“现在你会算三位小数乘两位小数、四位小数乘三位小数吗？……”一连串的问题，让学生反思、感悟到只要是小数乘法，其实算法都是通用的，以此从整体上帮助学生架构了一个完整的小数乘法知识体系（如图），同时学生思维的深度和广度也得到了发展。

二、循理入法，以理驭法，培养思维的批判性

思维的批判性，是指能够对问题、论述、证据等进行辩证性的思考，从而提出或形成自己的观点。批判性思维是一种审视真伪、理性推论的思维方式，不仅包含“独立思考”，还包含“真理多元”，如凭证据讲话、合乎逻辑地论证观点、善于提出不同问题、不懈质疑、对自身的反省和对异见的包容。

在《小数乘小数》一课中，算法与算理孰重孰轻？其实，算法、算理是运算能力的一体两翼，两者相辅相成，不可偏废。道理很简单，不掌握算法就无法确保实现运算能力的最低要求“正确”；只知怎样算，不知为什么这样算，充其量只是搬弄数字的操作技工。新授课中，我将重点放在如何让学生理解算理上，只要能理解算理，再跟进必要的练习巩固，算法的掌握便是水到渠成的事。

首先，在复习小数乘整数时，让学生进行竖式笔算1.6×35 ，并说出自己是如何算的。在说出算理之后，针对小数末尾有0的特殊情况适时评价：为什么一位小数乘整数，原则上乘积是一位小数，而这里却写了整数？

接着，在探究小数乘小数时，解决第一个问题：买0.9千克的橙子花了多少钱？学生自主尝试竖式笔算，并交流自己的算法。交流中，有学生质疑：为什么这道乘法运算，积变小了？还有学生问：为什么一位小数乘一位小数，积却是两位小数？解决第二个问题：买1.5千克的西红柿花了多少钱？学生自主尝试竖式笔算，请学生代表交流自己是怎么算的。交流中，有学生问：为什么7.88与1.5在竖式计算时没有将小数点对齐？还有的学生问：为什么两位小数乘一位小数，积却是三位小数？在给出“整数积”后直接说出“小数积”时，学生自主发现小数乘小数的规律：因数中一共有几位小数，积就有几位小数。有学生追问：为什么因数中一共有几位小数，积就有几位小数？这些核心问题的抛出，让学生在思辨中越辩越清，理越说越明。

由此看来，学生的思维状态决定着学生数学学习的整体效能，发展学生高阶思维是数学教学的应有之义。在数学运算教学中,教师可以通过创设学生学习的合理情境、建构学生学习的心理场境、打造学生学习的实践场域,引领学生深度体验、深度认知、深度实践,让深度学习真实发生！培养学生的高阶思维，是我们课堂教学中应努力追寻的方向！