氢、氧原子刻蚀CVD金刚石涂层石墨相的机理研究*

简小刚， 黄 新， 何嘉诚， 王俊鹏

(同济大学 机械与能源工程学院， 上海 201804))

CVD金刚石涂层在力学性能上与天然金刚石非常接近，具有较高导热系数、极高的硬度和较低的热膨胀系数，是加工超硬材料及制作深井石油钻探钻头最为理想的涂层材料之一[1-3]。金刚石涂层生长过程中基底的温度一般在800 ℃以上，一定程度上限制了基底材料的选择[4]。同时，金刚石涂层与基底间因热膨胀系数差异而引起的热应力会降低金刚石涂层与基底的附着力[5]。而降低制备金刚石涂层时的沉积温度虽然能够降低残余热应力的影响，但往往导致制备的金刚石涂层的质量不佳，金刚石涂层中的石墨相成分过多。

目前，研究人员多采用引入含氧气源的方式来降低高质量金刚石涂层的制备沉积温度，PETHERBRIDG等[6]在CO2/CH4气源中将CVD沉积温度降到了435 ℃；DAS等[7]也在455 ℃的富氩气环境中，往CH4/H2/Ar气源中通入0.75%的O2，从而制备了较高质量的金刚石涂层。大多数研究者认为氢、氧原子在低温下都能起到刻蚀金刚石涂层中石墨相的作用，同时氧原子刻蚀石墨的效果强于氢原子刻蚀的效果[8]。但对于氢、氧原子刻蚀金刚石涂层中石墨相的反应机理和作用机制仍然缺乏理论分析，没有对氧原子具有比氢原子更强的刻蚀石墨相能力的现象做出深入的探讨。

利用第一性原理分子模拟计算方法可以研究氢原子和氧原子刻蚀石墨相的反应机理与作用机制。相比一般的试验方法，采用第一性原理在密度泛函的理论基础上进行理论研究能够在微观尺度上探索原子间的作用关系，为氢、氧原子对CVD金刚石涂层中石墨相的刻蚀现象给出理论解释。

1 模型建立与计算方法

1.1 石墨相模型建立

采用分子动力学仿真软件Materials Studio建立石墨相分子结构模型[9]，该模型由石墨的单晶胞模型通过切取特定晶面后得到的超晶胞并建立真空层构成。

石墨相分子结构建模过程如图1所示：首先建立石墨的单晶胞模型(优化后的晶格常数为0.246 nm，与试验值0.246 nm[10]相符)；其次切取并建立2 ×2 (001)面石墨相超晶胞模型，其沿着坐标轴方向的尺寸为0.492 nm×0.492 nm。为简化计算量，在本计算工作中采用单层石墨烯来代替多层石墨结构，这种简化不会对表面刻蚀机理产生定性的影响。然后添加真空层(厚度为1.0 nm)构建三维周期性结构，最后建立石墨相分子结构模型(图2)。

图1 石墨相分子结构模型建模过程

图2 石墨相分子结构模型

氢原子进行刻蚀时，第一步反应中游离的氢原子吸附到石墨表面并与表面的碳原子成键，同时不破坏任何C—C键；第二步反应中另一个氢原子吸附到同一个碳原子上形成二氢化物，同时C—C键断裂，石墨结构逐渐被刻蚀破坏。氧原子刻蚀时，游离氧原子吸附到石墨表面并与表面的碳原子成键，同时C—C键断裂，石墨结构被刻蚀破坏。建立上述反应模型并进行几何优化，经过优化后的模型分别如图3、图4及图5所示。

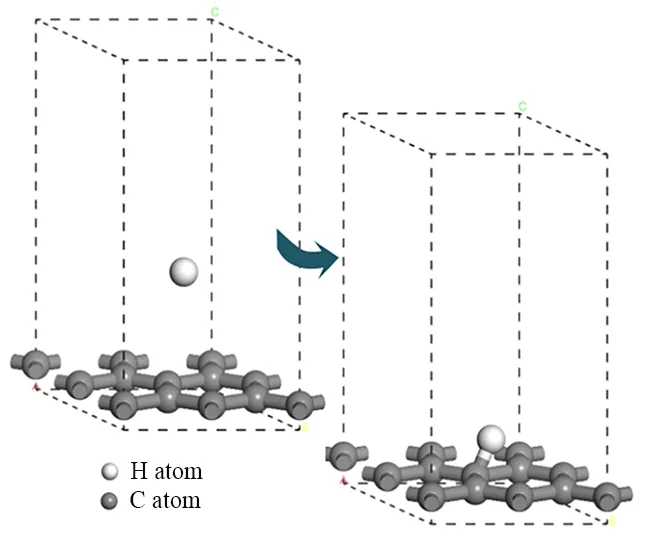
图3 氢原子刻蚀石墨相第一步反应

图4 氢原子刻蚀石墨相第二步反应

图5 氧原子刻蚀石墨相第一步反应

1.2 吸附能计算

基团粒子在基底表面吸附过程中，运动速度由快到慢并最终停止在基底表面上。由于粒子速度降低而导致动能中被释放出来的能量称为吸附能(adsorption energy)，其计算公式[11]：

Ead=-(Eall-Eslab-nxEsin)/nx

(1)

其中：Ead为基团粒子的吸附能；Esin为单个基团粒子的自由能；Eslab为基底晶体结构能量；Eall为吸附后基团粒子与基底结构体系总能量；nx为吸附粒子的数量。单个基团粒子自由能Esin的计算不同于基底晶体结构能量Eslab与吸附体系总能量Eall。单个反应粒子是孤立存在的，不具备连续性，也没有周期性结构。将粒子基团放置在晶胞的中心(图6)，晶胞要远大于粒子本身，以消除粒子的边界干扰[12]，这样就可以精确计算基团粒子的自由能。

图6 基团粒子自由能计算晶胞

在计算原子的自由能时使用Dmol3的Energy任务模块，布里渊区取样用Monkhorst-Pack方法1×1×1生成K点网格进行计算。计算Eslab与Eall时则使用Dmol3的Geometry Optimization 任务模块，采用3×3×1的K点网格进行采样。

1.3 过渡态搜索

过渡态搜索通过计算反应路径中的能量最低点，找到其活化络合物(过渡态)，从而计算出反应热和能垒。计算流程[13]如图7所示。建立反应物和生成物模型并进行结构优化；虚频的存在影响反应过程的稳定性，需要进行频率计算并消除虚频影响，确定反应物和生成物的稳定构型；建立反应过程预览动画，然后搜索过渡态，对过渡态进行频率分析，基于Nudged Elastic Band(NEB)算法，进行TS Conformation以LST/QST找到的过渡态为起点，在反应物和生成物方向上寻找局域能量最低点。

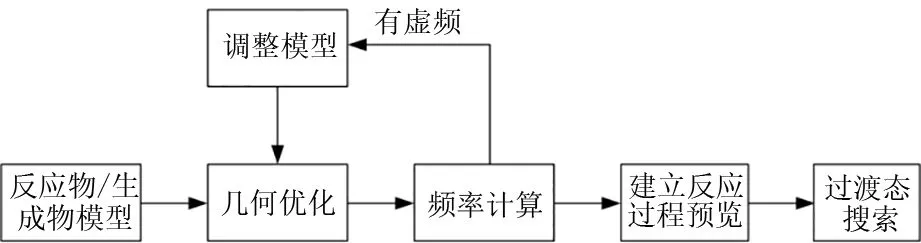
图7 过渡态搜索计算流程

2 仿真结果与分析

2.1 吸附能差异分析

仿真计算得到的氢原子与氧原子在石墨表面的吸附能如表1所示。

表1 氢原子与氧原子在石墨相表面吸附能

不难发现：氢原子与氧原子都能和石墨表面形成吸附态，且氧原子在石墨相表面的吸附能0.496 eV高于氢原子吸附能0.128 eV。吸附能也在一定程度上反映出氧原子和氢原子可能吸附到石墨相表面的概率[14]。基团在石墨表面的吸附是基团与石墨发生反应而解离C—C键，进而刻蚀金刚石涂层表面石墨相的前提。

对几何优化后的氢原子、氧原子和石墨结构的轨道能量进行计算分析后得到前线轨道能量表(表2)。最高占据轨道(HOMO)与最低未占据轨道(LUMO)能量差值的大小代表结构体系发生化学变化的难易程度，差值越大则反应活性越低[15-16]。

表2中氧原子的最高占据轨道与最低未占据轨道的能量差值大小小于氢原子的，这意味着氧原子的化学反应活性强于氢原子，更容易同石墨结构表面形成电子转移反应。由于氧原子的最高占据轨道能量绝对值强于石墨结构的且氧原子最低未占据轨道能量接近石墨最高占据轨道能量，结合前线轨道理论的能量相近原理可知[17]，当氧原子在石墨结构表面形成吸附态时，应当主要由石墨结构的LUMO轨道和氧原子的HOMO轨道起作用，即电子从氧原子转移至石墨结构中的碳原子。

表2 前线轨道能量表

2.2 反应热和能垒

由过渡态搜索计算结果可得氢原子与氧原子在石墨表面反应的反应热与反应能垒如表3所示。其中反应热为负值表示反应为放热反应；反应能垒代表此反应发生需要多少能量，反应能垒越小，表明反应需要的能量越少，反应越容易发生。

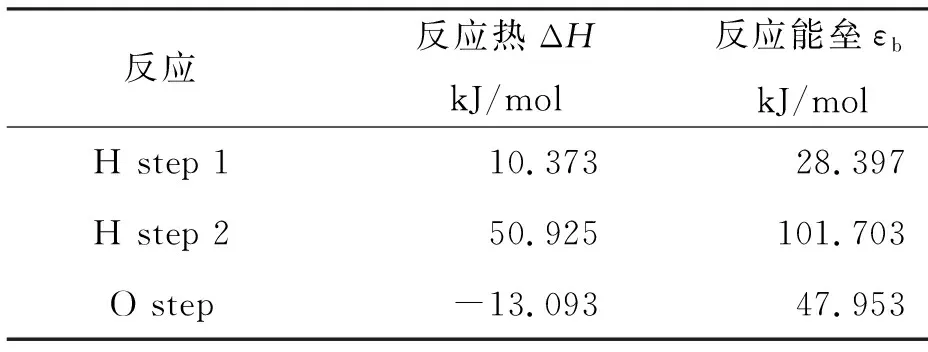
表3 氢、氧原子在石墨表面反应热与反应能垒

氢原子刻蚀CVD金刚石涂层表面石墨相的第一步反应(H step 1)为吸热反应，反应热为10.373kJ/mol，此反应中游离的氢原子吸附到石墨表面并与表面的碳原子成键，同时不破坏任何C—C键，碳氢键C—H从石墨平面伸出，电子结构由sp2轨道变为sp3轨道，反应能垒为28.397 kJ/mol。氢原子刻蚀CVD金刚石涂层表面石墨相的第二步反应(H step 2)也为吸热反应，反应热为50.925 kJ/mol，此反应中另一个氢原子吸附到同一个碳原子C上形成二氢化物，同时C—C键断裂，石墨相结构逐渐被刻蚀破坏，此反应的反应能垒为101.703 kJ/mol。

氧原子刻蚀CVD金刚石涂层表面石墨相反应(O step )为放热反应，反应热为-13.093 kJ/mol，此反应中游离氧原子吸附到石墨表面并与表面的碳原子成键，且键长为0.122 nm，接近C=O键理论键长0.120 nm。表明氧原子与碳原子成C=O键，成键同时有C—C键被破坏断裂，剩余的两个C—C键电子结构由sp2轨道变为sp3轨道，稳定的石墨结构被刻蚀破坏，此反应的反应能垒为47.953 kJ/mol。

分析各反应的反应热和反应能垒可以发现氢原子刻蚀的第一步反应的反应能垒最低，所以氢原子刻蚀石墨相的反应最容易发生。而对于氧原子而言，虽然其刻蚀石墨相的反应能垒相比氢原子第一步反应能垒而言较高，但是氢原子促使石墨相表面的C—C键断裂需要两步反应，而氧原子促使C—C键断裂只需要一步反应，氢原子刻蚀石墨相的总能垒比氧原子的高，这为氧原子具有比氢原子更强的刻蚀石墨相能力的现象提供了解释。

3 结论

基于第一性原理分子模拟计算理论，采用Materials Studio软件对氢原子和氧原子刻蚀石墨相的反应机理与作用机制进行研究并得到以下结论：

(1) 刻蚀基团氢原子与氧原子都将和石墨表面先形成物理吸附。氧原子在石墨相表面的吸附能0.496 eV略强于氢原子吸附能0.128 eV; 同时前线轨道能量计算结果表明氧原子的化学反应活性强于氢原子，更容易同石墨结构表面发生电子转移反应。

(2)氢原子促使石墨相表面的C—C键断裂需要两步反应，两步反应的反应能垒分别为28.397 kJ/mol与101.703 kJ/mol，而氧原子促使C—C键断裂只需要一步反应，反应能垒47.953 kJ/mol。因此，氧原子刻蚀石墨相的反应总能垒比氢原子刻蚀的低，反应所需能量更少，说明氧原子具有比氢原子更强的刻蚀石墨相能力。