一种基于密度峰值聚类的链路预测算法

邵 豪，王伦文，邓 健

1(国防科技大学 电子对抗学院，合肥 230031)

2(陆军工程大学 石家庄校区二系，石家庄 050003)

E-mail：shaohao64@outlook.com

1 引 言

随着复杂网络理论的迅速发展，网络在社交、军事、信息等领域得到广泛应用[1].获取完整的网络拓扑结构是分析、控制网络的基础[2]，但条件的局限会导致网络重构不完整.链路预测不但预测网络中的丢失链接，而且也可预测演进网络中可能出现的未来链路.社交网络中，推荐尚未存在的链接作为潜在的友谊关系，可以帮助用户寻找新朋友[3].战场通信网中，链路预测作为网络拓扑侦察的补充，预测敌方通信网络还未侦察到的链接，以及敌方通信节点间的隐藏链接，为网络对抗提供条件[4].

最常用的链路预测算法是衡量两节点的相似性，相似性更高的节点间更可能存在链接[5].相似性指标作为衡量节点相似的标准，不同指标直接影响链路预测的精度.分析节点外部属性已被广泛使用且有较高的预测精度[6]，但实际中，节点的属性信息通常是难以获取的.例如，社交网络中用户的个人信息受到隐私保护；战场通信网中，敌方节点信息是加密的[7].考虑到网络结构信息更容易获得，近年来，基于网络结构的链路预测方法逐渐成为研究的热点，刘大伟等人[8]提出局部差异融合算法，共同考虑节点共同邻居集合的相似性与差异性以提高预测精度；许忠齐等人[9]提出加权路径熵(WPE)，比较路径熵对预测精度的贡献；此外，姚亚兵等人[10]提出利用“层相关性”来对多层网络进行链路预测.

上述算法都提出了一个改进的相似性指标来预测链路，在特定网络中有较好的预测性能.事实上，不同网络具有截然不同的结构特征，甚至同一网络不同部位的结构也是明显不同的[11].因此，单个相似性指标不可能在所有网络中都有很好的预测性能.Ma C[12]提出一种结合多种结构指标的方法，首先定义一个包含多个结构指标的函数，然后利用已知结构信息来确定函数中每个特征的权重.在本文中，我们提出一种自适应融合多个相似性指标的链接预测算法，利用无监督机器学习对未知链路进行分类，依据分类结果完成链路预测.实验结果表明，在不同网络中，本文提出的自适应链路预测算法普遍具有良好的预测性能.

2 相关知识

2.1 网络定义

无向网络G(N，E)，N是节点集，E是链路集.若节点i、j之间存在链接，则aij=1；反之aij=0.Γ(i)表示节点i的邻居节点集合，ki表示节点i的度.

聚类系数ci表示节点i的邻居节点间连接的紧密度[13]，其定义为某节点所有邻居节点间的链接数目与可能产生的最大链接数目之比.

(1)

其中，li表示ki个邻居节点间存在的链路数目.当ci=1时，节点i所有邻居节点两两链接.

2.2 密度峰值聚类

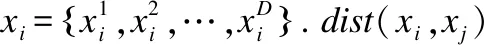
①密度大，即被不超过其密度的节点包围；

②与其它更高密度的节点间有更大的距离.

本文使用密度峰值聚类对节点间的未知链路进行分类，主要考虑以下几方面：

①不同网络的结构差别很大，未知链路的属性分布不是凸 型的.与层次聚类和划分式聚类不同，密度聚类可以发现各种形状和各种大小的簇[15].

②传统密度聚类DBSCAN算法的性能对于半径、阈值这两个初始参数敏感，且难以发现不同密度的簇；OPTICS算法在可视化图中寻找“山谷”来确定簇，处理方式复杂，运算速度慢.考虑不同网络的结构，很难有一个固定的合适参数.

③密度峰值聚类算法基于相对距离和相对密度来分析数据点，能够分类不同密度的簇，且时间复杂度比其他密度聚类算法更低，针对不同结构的网络更具适用性.

密度峰值聚类中，如果一个簇密度分布均匀或有多个高密度点，可能会把某些簇分成几个子簇.本文链路预测算法中，分类结果为有链接、无链接两类，因此即使发生簇过分类，通过对比簇中心节点的相似性指标，进行簇合并，得到正确的聚类个数，避开了密度峰值聚类可能产生的过分类的缺陷.

3 链路预测算法与实现

3.1 链路预测问题描述

U表示一个无权向网络G(N，E)中包含所有可能链接的集合，即|U|=[|N|·(|N|-1)]/2.网络中未知链接的集合(存在但未被发现的链接)是V，已被发现的链路集是U-V，链接预测的任务就是找出未知链接.传统的链路预测算法，通过计算出节点间的相似指标值sij，将所有未知链接以值从大到小排列.sij越高，两节点间存在链接的可能性也越大.一些基于邻居节点的局部相似性指标[16]如表1所示.

表1 部分基于邻居节点的局部相似性指标

表1中，CN认为节点间存在链接的概率随着其二阶路径的个数增加而增加，JC、AA、RA在不同方面改进CN指标.JC认为应该考虑二阶路径个数的比例，AA、RA认为即使是相同个数的邻居点，不同邻居节点会存在不同贡献度，即不同的二阶路径拥有不同的贡献度，通过惩罚度更大的邻居节点来区分相同的二阶路径.

除上述指标外，本文还考虑局部随机游走的相似性指标LRW[5].定义πxy是一个随机游走粒子t时刻在节点x处，t+1到节点y处的概率，得

πx(t+1)=PTπx(t)t≥0

(2)

其中，πx(0)是第x个元素值为1，其余值为0的向量，P是马尔可夫概率转移矩阵.网络节点最初资源分布为qx，则LRW指标可表示为：

sij(t)=qx·πxy(t)+qy·πyx(t)

(3)

本文认为网络节点最初的资源分布是平均的，即qx=kx/|E|.最终：

(4)

本节介绍了链路预测的目的，以及部分节点相似性指标，分别是基于邻居节点相似性和局部随机游走.虽然这两个指标在特定网络中有较好的性能，但由于网络的多样性，单个相似性指标不可能在结构不同的网络中都有很好的预测精度.因此，将上述介绍到的相似性指标作为节点对的某一维度的参数综合考虑.除上文介绍到的相似性指标之外，本文还提出改进的路径相似性指标进行预测.

3.2 改进的路径局部相似性指标PLD和INR

全路径相似性指标Katz分析网络中节点间所有路径的数量，预测精度较高，但因需要网络全路径信息，时间复杂度很高[7].局部路径指标LP考虑有限长度的路径，综合预测精度和时间复杂度，但其只分析中间节点的邻居数量，未完全挖掘路径结构信息[8].为此，本文提出两个改进的路径局部相似性指标PLD(Path Link Degree)及INR(Intermediate Node Ring)，分别考虑路径中间链接及中间节点连通性对预测的贡献，相比传统局部路径预测指标，考虑了更多的路径信息，提升了预测精度.

3.2.1 PLD指标

网络G(N，E)中，若某条链路exy存在，定义链接exy的度为：

kexy=kx·ky

(5)

其中，kx、ky表示为链接exy两端节点x、y的度.文献[17]表明，节点度与链路预测精度成反比关系.即已存在的链接会对相应的节点对的链路预测成功率产生影响.因此首先定义 SLD(Single Link Degree)指标衡量一条链路对预测精度的贡献：

SLD=(kexy)-θ=(kx·ky)-θ

(6)

其中，θ是一个固定的参数.本文中θ=1，即LD=(keij)-1=(ki·kj)-1.由此定义了一条链路对于链路预测的贡献.

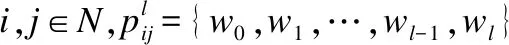
(7)

式(7)可看出，一条路径的SPLD指标值等于该条路径中每条链路的SLD指标值之和.遍历节点i、j间的所有路径，最终PLD指标定义如下：

(8)

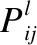
(9)

3.2.2 INR指标

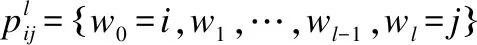
(10)

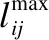
(11)

3.3 链路预测算法与实现

3.3.1 算法思想与指标筛选

前文介绍，通过单个相似性指标得到的网络预测性能与网络结构直接相关.针对于同一网络，不同相似性指标基于不同的角度，会得到不同预测结果，存在相应交集.文献[12]指出，不同指标得到的预测性能是无法通过简单的合并或求交集来提升的.例如，图1中左右两个圆分别表示CN，JC两个指标在Hep-ph网络上的预测结果的集合[12].表2表示这两指标预测准确率及并集、交集后的准确率.

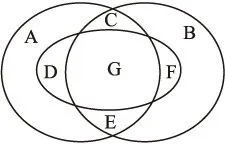
图1 CN，JC指标预测结果集合

表2可得，预测准确率、并集准确率、交集准确率无直接关系.随意将不同相似性指标的预测结果求并集，会大大增加虚警率(将没有链接的节点对误判为有链接)；将不同相似性指标的预测结果求交集，会大大增加漏警率(忽略有链接的节点).

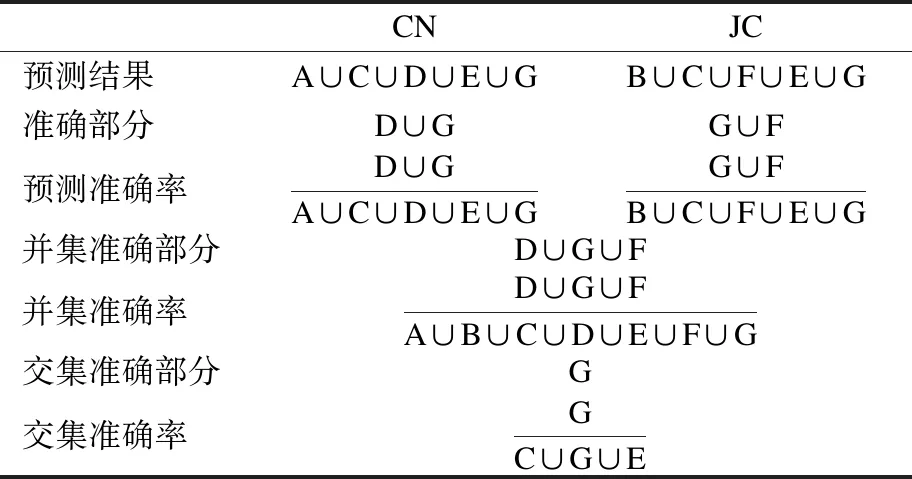
表2 CN、JC指标预测并集、交集准确率

与单纯的并集或交集不同，本文提出一种利用无监督机器学习的链路预测算法，将不同的相似性指标作为节点的多维参数，利用密度峰值聚类，综合各指标对节点进行分类.以下讨论选取哪些相似性指标作为节点的聚类参数，统筹效率与预测精度.

本文算法中，考虑到聚类分类精度，尽可能使用相对独立的指标作为各维参数.本文使用JC，RA，LRW，PLD，INR这5个指标作为节点间的聚类参数，主要考虑以下几方面：

①所有指标都只考虑局部相似性特征，全局特征会增加复杂度，且预测性能提升有限，不适用于大规模网络.

②JC、RA基于节点局部相似性，特别是两端节点的邻居节点性质；LRW基于随机游走模型； PLD、INR分别考虑到节点对之间路径与节点信息.这5个参数尽可能包含节点多的信息.

③JC是CN指标的改进，RA和AA都以共同邻居的度作为惩罚指标，因此二选其一，避免指标重复.

3.3.2 聚类结果属性判定

本文聚类结果应分为有链接或无链接，其有无链接的属性判定遵循以下两个标准：聚类结果包含的对象数目以及聚类结果中的特殊链路.以下进行具体分析：

① 网络中的节点普遍只与部分邻居节点相连，即|E|≪[|N|·(|N|-1)]/2，网络中存在链接的节点对数目远小于节点对总数.更重要的是，在链路预测的仿真与实际应用中，大部分链路已知，未知链路只占所有链路的小部分.因此聚类后，两节点间存在链接的分类包含的对象数目应远小于不存在链接的数目.例如，若聚类后两类中对象数目分别占总数的5%与95%，则将5%的分类作为有链接的分类.

② 对于两个节点，指标值sij越大，则链接存在的可能性越高.如果这两节点的所有指标值都很高，则可以认为链路是存在的，其所在聚类结果的属性也可以确定.

综上所述，在本文算法中，将聚类中对象数目少、存在所有指标值都很高的对象的分类判定为链路存在.

3.3.3 算法步骤

本文提出的基于密度峰值聚类算法步骤如下：

输入：无权向网络G(N，E)，所有未知链路集合V(集合元素vij表示节点i、j组成的节点对).

输出：未链接节点对是否存在链路.

1.fori=1to|N|forj=1to|N|；

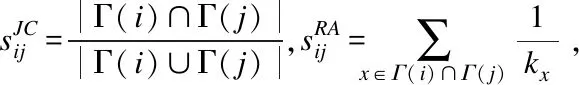
3.form=1to|V|forn=1to|V|；

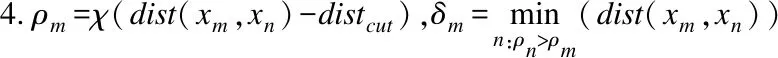
5.按照聚类结果，确定被分类为有链接的节点对并输出.

4 实验分析

4.1 实验数据与流程

为分析本文算法的性能，本文使用6种网络结构进行实验分析，分别是美国航空网络US Air(机场间的航线信息)，海豚网络Dolphins(海豚间的亲密关系)，政治博客网络Political Blogs(博客页面间的链接)，铁线虫神经网络Celegans(铁线虫神经突触)，爵士乐Jazz网络(音乐家的合作关系)，科学家网络NS(科学家的合作关系).网络数据来源：http://konect.uni-koblenz.de/networks/；http://www-personal.umich.edu/～mejn/netdata/；http://networkrepository.com/networks.php.网络参数如表3所示.

在实验中，为测试算法性能，将网络G(N，E)中的链接分为两部分：训练集ET和测试集EP.ET∪EP=E，ET∩EP=∅.首先，有权向的网络改为无权向，将6个网络中部分链接划分为ET，其余作为EP.随后，分别计算6个网络U-ET中所有未知链路CN、JC、RA、AA、LRW、PLD、INR指数，得 到各指标的相似性值；再以JC、RA、LRW、PLD、INR指数作为未知链路的多维参数，标准化与归一化后，使用本文提出的基于密度峰值聚类的预测算法，对未知链路进行无监督分类，得到所有节点对的连接情况.有链接的节点间相似性指标值sij为1，反之为0.

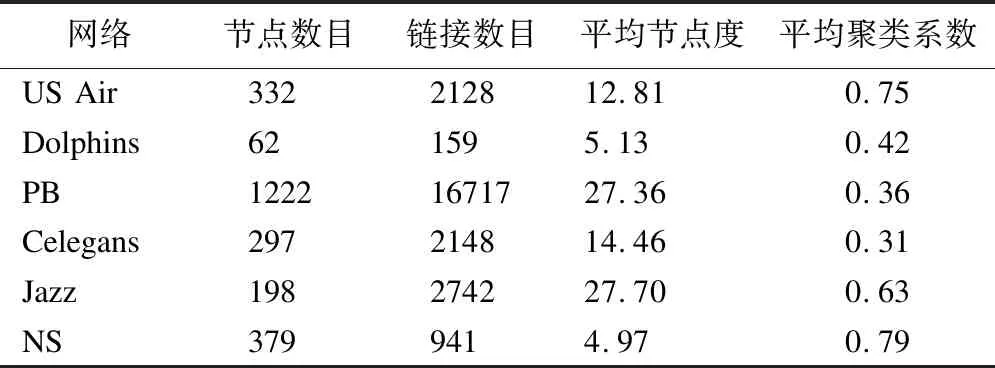
表3 网络参数性质

AUC是一种广泛使用的链路预测算法评价标准[18].AUC表示从测试集EP中随机选择一条链路的相似性指标值sij比从预测节点对集合U-E中随机选择一条链路的sij值高的概率，即：

(12)

其中，n是随机选择的次数n′是测试集sij值大于U-E集合的次数，n″是值相等的次数.本文算法最终得到聚类结果，sij是定性的二进制值(0、1)，因此本文算法的AUC可等效为未知链路集合U-E的预测准确率，即：

(13)

4.2 实验结果

4.2.1λ对PLD、INR指标的影响

本文提出两种路径相似性指标PLD和INR.3.2节已介绍二阶路径信息对预测贡献度大于三阶路径，故λ∈(0，1).λ值直接影响PLD和INR的预测准确率.为确定合适的λ值，在(0，1)范围内，以0.1作为步长，选取不同λ值，以PLD和INR指标进行预测，并计算相应预测评价标准AUC.

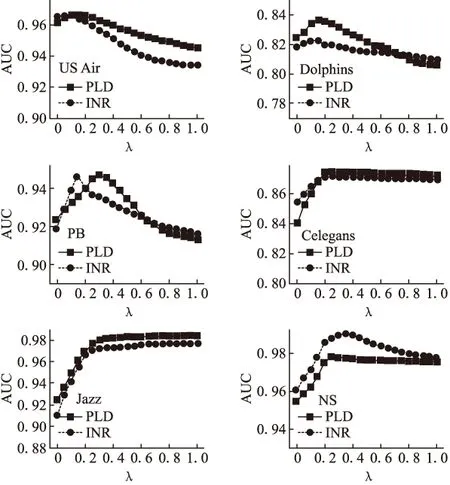
图2 各网络中λ对PLD、INR指标的影响

图2表示PLD、INR指标在各网络中的预测性能，AUC值越高，预测准确率更高.λ=0时，只考虑网络的二阶路径信息.随着λ增大，网络的三阶路径信息在指标中的地位越发重要，直至λ=1时，地位与二阶相同.在λ增大的初始阶段，PLD、INR指标的AUC在不同网络中都上升，说明与仅使用二阶路径信息相比，适当考虑三阶路径信息是有必要的，能够提升预测准确率.但随着λ继续上升.US Air、Dolphins、PB、Celegans、NS网络的预测性能都发生不同程度下降，这是因为这些网络平均密度较低，网络稀疏，三阶路径信息成为了预测的噪声信息.而在NS网络中，高密度意味着节点间的联系紧密，两节点间三阶路径较为普遍，因此三阶路径信息有利于提高预测准确率.

理论上，短路径对预测的贡献高于长路径，λ在[0，1]的范围内，预测性能有一个高点，考虑到各网络结构不同，最优λ不同.根据图2，取λ=0.2作为式(9)、式(11)的三阶路径信息权重，此时在不同网络中，PLD、INR指标都能有较好的预测结果.

4.2.2 算法性能对比

将网络中90%的链路作为训练集ET，其余10%作为测试集EP.按照4.1节介绍的实验流程，得到各算法的预测结果，并计算相应AUC值，以衡量本文算法的预测性能，具体AUC值如表4所示.

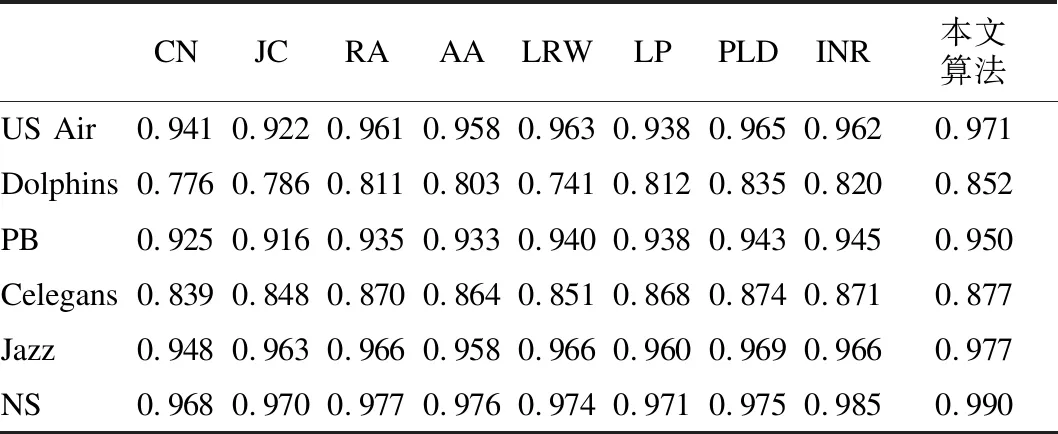
表4 各预测算法在不同网络上的AUC值(90%训练集)

表4表示训练集比例为90%时，不同算法的预测精度.一方面，本文提出的改进路径局部指标PLD和INR，与传统局部路径指标LP相比，预测准确率分别提高1.2%、1.0%，这说明PLD、INR指标通过考虑路径中间链接及中间节点连通性对预测的贡献，克服传统LP指标只考虑中间节点的邻居数量，未能完全挖掘路径信息的缺陷，有效提高了预测的精度.另一方面，与传统的链路预测算法相比，本文提出的基于密度峰值聚类的预测算法的精度在各网络中都有提高.较节点局部相似性CN、JC、RA、AA算法，本文算法分别提高3.7%、3.5%、1.7%、2.1%；较随机游走模型LRW算法提高3.0%，较路径相似性LP、PLD、INR算法分别提高2.2%、1.0%、1.1%.本文算法在各网络中都能达到最佳的链路预测性能，说明利用密度峰值聚类的算法，融合考虑不同节点相似性指标，在预测时获得更加全面的网络结构信息，从而有效地提高了预测精度.

为综合衡量算法性能，将训练集ET的比例由90%改为80%，重新进行上述实验流程，得到各预测算法的AUC值，如表5所示.为详细比较各预测算法在不同比例训练集时的差别，将表4与表5中各AUC值相减，得到不同训练集比例时各预测算法精度的差值，如图3所示.

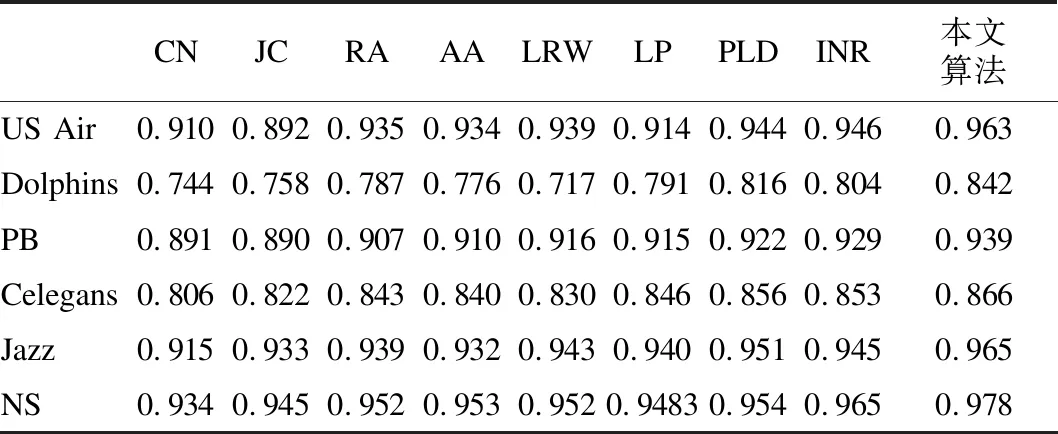
表5 预测算法在不同网络上的AUC值(80%训练集)

表5表示80%训练集时，各算法在不同网络下的预测精度AUC.当训练集从90%减少到80%时，所有预测算法的AUC都降低，这是因为训练集比例减小，导致预测时获取网络信息减少.例如CN算法中，训练集中邻居节点的减少，致使共同邻居数目减少，预测精度降低.对比而言，无论训练集比例是80%还是90%，本文算法都有很好的预测精度.

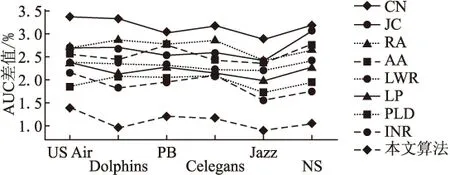
图3 各算法在90%与80%训练集的AUC差值

图3表示各算法在训练集分别为90%与80%比例时AUC差值，数值越小，说明在训练集减少的情况下，预测性能降低越小.横向来看，在Jazz网络中，所有算法AUC都下降最小，这是因为Jazz网络拥有较高的网络密度，在80%训练集的情况下，节点间能够有较好的连通性，预测时存在更多的链路信息.纵向来看， CN、JC、RA、AA算法都下降幅度明显，说明训练集减少对节点邻居的相似性指标影响较大，基于路径的PLD、INR算法较随机游走LRW算法受训练集减少影响较少.基于密度峰值聚类的算法与其他所有算法相比，在各个网络中AUC差值最小，说明本文算法在训练集降低的情况下，预测性能下降很小，更能适应复杂环境.

5 总 结

由于链路预测不同指标具有互补性，不同的相似性指标综合可以有效地提高链路预测的精度.为此，本文提出一种基于无监督机器学习的链路预测算法，给出两种改进的路径相似性指标以提升预测性能，并将这两指标与节点邻居局部相似性指标、随机游走指标作为未知链路的不同维度信息，然后使用密度峰值聚类对所有未知链路进行无监督学习，进行每条未知链路的链路预测.仿真实验表明，相较传统预测指标，本文算法在不同的网络中都具有很高的识别精度，证明了算法的有效性.在训练样本占总样本比例较小的情况下依然能够得到较高的预测精度.本文的主要贡献是将无监督的机器学习引入到了链路预测中，下一步，将考虑引进其他相似性指标进一步提高链路预测精度.