模拟退火算法优化PSO-GA算法解决柔性流水车间调度问题

景会成，王 颖

(华北理工大学 电气工程学院，河北 唐山 063210 )

E-mail ：925683837@qq.com

1 引 言

柔性流水车间调度问题(Flexible Flow Shop scheduling，FFSP)是数字化车间首要解决的问题，是大量实际生产调度问题中最常见的简化模型，是一类重要的组合优化问题，已经成为先进制造技术实践的关键[1].FFSP问题可以被描述为一批工件需要经过n道工序在m台数控机床上进行加工，其中n道工序有一定的先后顺序，m台数控机床存在并行情况.由于实际生产过程中n、m的数值往往比较大，FFSP问题成为典型的NP-hard问题.目前针对于FFSP问题的解决方法有很多.韩忠华[2]等采用最优个体集和自适应位置更新对蝙蝠算法进行优化的方法对FFSP问题求解.毕孝儒[3]等采用混沌算子对人工群峰算法进行优化的方法对FFSP问题求解.张海月[4]提出了模拟退火扰动(SADA)算法与NEH贪婪搜索算法结合后对粒子群算法进行优化的方法对FFSP问题求解，上述文章都对经典的算法进行了优化，但依然存在着一个局部最优和收敛速度之间的对立，若过于追求收敛速度，则可能限于局部最优，为了防止局部最优，必然会影响到收敛速度.本文针对FFSP问题提出了一种改进的遗传算法，针对于传统遗传算法收敛速度慢的问题对未能直接进入下一代种群的剩余个体采用粒子群算法(PSO)，该算法能够加快收敛速度.针对于传统遗传算法局部搜索能力弱容易限于局部最优的问题在迭代过程引入模拟退火算法(SA)，该算法能够概率性的跳出局部最优解并最终趋于全局最优.改进后的遗传算法能快速、高效的解决FFSP问题.

2 车间数学模型

车间共有m台机床，机床号集M={M1，M2，M3，…，Mm}，令i∈{1，2，3，…，m}，则Mi表示机床号为i的机床.有n个待工件，待加工工件集N={N1，N2，N3，…，Nn}，令j∈{1，2，3，…，n}，则Nj表示第j个未加工工件.工艺路线集L={L1，L2，L3，…，Ll}，其中l∈R.Nj可以在不同的Mi上加工，并且一旦开始加工便不能停止.Nj需要Oj道加工工序，工序顺序集P={Pj1，Pj2，Pj3，…，PjOj}，令k∈{1，2，3，…，Oj}则Pjk表示Nj在第k道工序加工，Tjk记为Nj在第k道工序加工对应的加工时间，Sjk记为Nj在第k道工序加工对应的加工时间，STik记为Mi在第k道工序的起始加工时间，ETik记为Mi在第k道工序的加工结束时间.Cmax为车间排产调度的最大完成时间，Cj记为Nj所有工序加工完成时间.Cjk记为Nj在第k道工序的总完成时间.Cj的具体表达式：

(1)

其中

Cjk=Sjk+Tjk

(2)

目标函数

f=min{Cmax}=min{max(Cj)}j∈{1，2，3，…，n}

(3)

约束条件

Tj(k-1)≤Tjk(k≥1)

(4)

STik≥ETi(k-1)(k≥1)

(5)

公式(3)中f为最小完工时间，使Cmax达到最小即找出最优的加工方案使总加工时间最小.k-1道工序的结束时间先于第k道工序的起始时间，保证工序的先后顺序不变.Mi在第k-1道工序的加工结束时间先于Mi在第k道工序的起始加工时间，保证一台机床只能加工一个工件.

3 PSO-GA算法改进

粒子群优化算法最初是由Eberhart和Kennedy在1995 年提出的，是基于迭代的优化方法，可用对复杂问题优化求解[5]，粒子群里的个体(即粒子)代表问题的一个可能解，每个粒子具有位置和速度两个特征，粒子通过位置来决定自身的适应度各个粒子记忆并追随当前的最优解.

把规定了行为规则的粒子作为个体，多个个体组合成为一个复杂的群体，便可用来对FFSP问题求最优解.Xi=(xi1，xi1，…，xiD)记为第i个粒子的位置；Vi=(vi1，vi1，…，viD)记为第i个粒子的速度；Pg(k)=(pg1(k)，pg2(k)，…，pgD(k))记为经过k次迭代后的粒子i的最优位置；Pg(k)=(pg1(k)，pg2(k)，…，pgD(k))记为次迭代后的最优粒子的位置.

vid(k+1)=ω·vid(k)+c1·r1·[pid(k)-xid(k)]+

c2·r2·[pgd(k)-xid(k)]

(6)

(7)

xid(k+1)=xid(k)+vid(k+1)

(8)

其中c1、c2为加速因子，ω为惯性因子，r1∈[0，1]、r2∈[0，1]、d∈[1，D]，D表示粒子群搜索空间的维数.从上述公式可以看出PSO在迭代中期的收敛速度快、搜索效率高、精度高但在其他时期搜索效率低，在迭代后期更新速度几乎趋近于0，容易陷于局部极值.最初由美国Michigan大学Holland教授于1975年首先提出来的遗传算法(Genetic Algorithm，GA)，是通过对自然进化过程进行模拟来实现搜寻最优解的一种方法[6].遗传算法具有很强全局寻优能力，尤其在迭代前期进化速度很快.这对于两者的优缺点很多学者提出了粒子群优化遗传算法对两种算法进行优势互补.本文对文献[7]中提出的PSO优化遗传算法进行了改进.

3.1 染色体编码

在黄志清[8]等提出的双层编码的思路上，对工艺路线的工序数进行定量后对染色体进行编码.基因Njlk表示工件Nj的l条工艺路线的k道工序.假设车间有4条工艺路线L1、L2、L3、L4，8个工件N1、N2、N3、N4、N5、N6、N7、N8进行加工.第一层编码4-2-1-1-3-1-4-3，第二层编码为1-1-3-5-3-8-1-7-8-5-2-4-2-6-2-8-6-2-4-3-7-8-5-2-8-5-5-4-2-6，其中工艺路线L1拥有3道工序，L2拥有6道工序、L3拥有5道工序、拥有2道工序.最终编码为：

N141-N311-N531-N312-N831-N142-N741-N832-N532-N221-N411-N222-N611-N223-N833-N612-N224-N412-N313-N742-N834-N533-N225-N835-N534-N535-N413-N226-N613

3.2 适应度函数及选择操作

适应度函数的选择的原则是，适应度函数大于等于0，同向于优化方向，并且一般在目标函数的基础上进行变换.对完成时间进行去量纲处理后得到最大完工时间CTmax最小完工时间CTmin.适应度函数如公式(9)所示：

(9)

采用轮盘赌局的方式，根据Fit函数对个体的适应度进行计算，然后按照适应度值对应的选择概率进行随机选取，一直到选出满足设定数量的个体数[9,10].

3.3 交叉和变异操作

交叉和变异操作的目的是产生新的个体保证种群的多样性，其中遗传算法的全局搜索能力由交叉操作控制，局部搜索能由变异操作决定.

交叉操作是对父代个体配对进行基因交换重组，产生新的个体，从而使更优个体出现成为可能[11]，交叉因子pc1的取值对遗传算法的收敛性有很大的影响，若pc1取值过小，进化缓慢不利于个体的优胜劣汰，若pc1取值过大，新个体产生的速度加快但同时增大了个体迅速被破坏的风险.所以此次采用了自适应交叉因子.

保证最大适应度值与平均适应度值不相等时的基础上，当前适应度值Fit(x)高于平均适应度值Fitavg时给pc0乘上一个小于1的数，减小交叉因子pc1的数值使优秀个体能够进入下一代.

(11)

变异操作是通过对个体内部基因的更改产生新的个体，自适应变异操作公式与交叉操作类似.

4 模拟退火算法

模拟退火算法(Simulated Annealing，SA)最早的思想是由N.Metropolis[12]，通过赋予搜索过程一种时变且最终趋于0的概率突跳性，来有效的避免陷于局部极小并最终趋于全局最优的串行结构的优化算法.将模拟退火算法应用于遗传算法的迭代过程中加入SA判断函数用来确定是否执行SA操作，SA算法的步骤如下：

1)初始化参数设置：初始解S、初始温度T、迭代次数L、循环计数器K；

2)Metropolis准则.增量ΔT=C(S′)-C(S)，C(S)为评价函数；

3)ΔT判断.若T<0，S′变为当前解，若ΔT≥0以概率exp(-ΔT/T)接受S′变为当前解;

4)终止条件判定：根据经验若连续K个新解都没有被选择，那么当前解为最优解输出并结束.如果不满足终止条件那么进行降温操作.降温公式为：

tW=γtW-1

(12)

5)重复上述步骤，完成对所有个体抽样.

5 SA优化改进PSO-GA算法

前期利用遗传算法前期搜索效率高的优势产生初始种群，前期迭代次数所占总次数的百分比为GAΦ，中期利用粒子群算法收敛速度快的特点进行中期迭代，中期迭代次数所占总次数的百分比为PSOΦ，后期利用模拟退火算法来避免PSO-GA后期容易陷入局部极值的问题，后期迭代次数百分比为SAΦ，且PSOΦ+GAΦ+SAΦ=1.参数初始化时需要根据经验设定了GAΦ、PSOΦ、SAΦ的值.SA优化PSO-GA算法以下简称SA-PSO-GA算法流程图如图1所示.

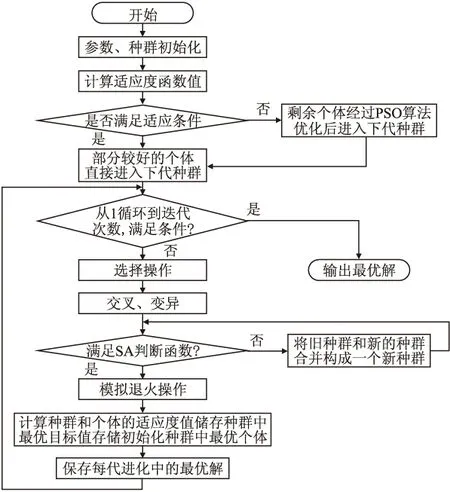
图1 SA-PSO-GA算法流程图

首先进行参数初始化设置并由遗传算法产生一个初始种群，计算适应度函数对满足条件的直接进入下一步，不满足的通过PSO优化之后进入下代种群.中期对种群选择、交叉、操作等操作进行迭代，后期对符合SA判断函数条件的进行模拟退火操作，不满足的通过对旧种群与新种群合并成新的种群的再判断是否满足SA判断函数.进行适应值判断后保存每代进化的最优解直到输出最终的最优解.

6 生产车间调度实例仿真

赣州某机器人生产车间负责对6kg、8kg、12kg、20kg等多种型号的工业机器人本体件的加工工作.工业机器人本体由大臂、小臂、转座、腕部、手部等组成.采用该公司提供的8kg机器人本体件，6个工件每个工件6道工序的数据进行排产实验.定义8kg机器人型号对应的工艺路线l为0.表1所示为该公司应用案例中各工件加工时间.

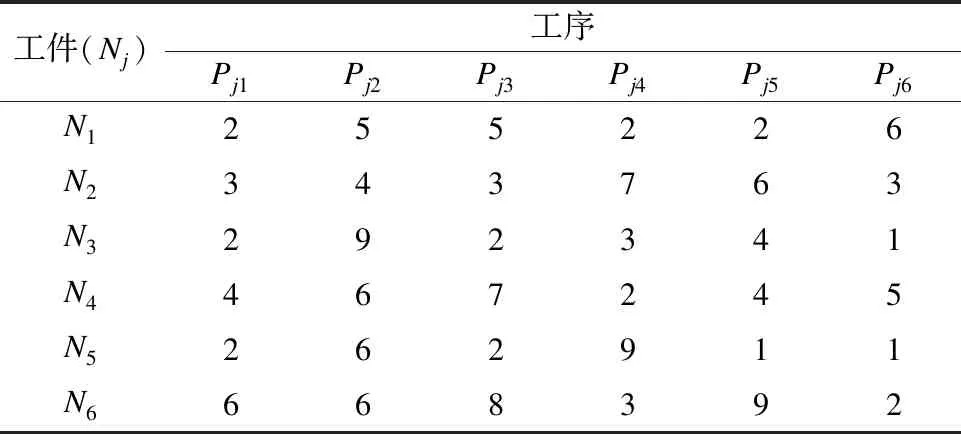
表1 工业机器人本体加工车间部分工件加工时间(h)

对改进PSO-GA算法进行排产的初始粒子数为50、迭代次数150、pc0为0.85、pm0为0.35、γ为0.95.SA优化PSO-GA算法进行排产的初始粒子数、迭代次数、pc0、pm0不变，模拟退火初始值500、模拟退火终值0，两种算法对应甘特图分别如图2、图3所示.甘特图用jlk表示Njlk.

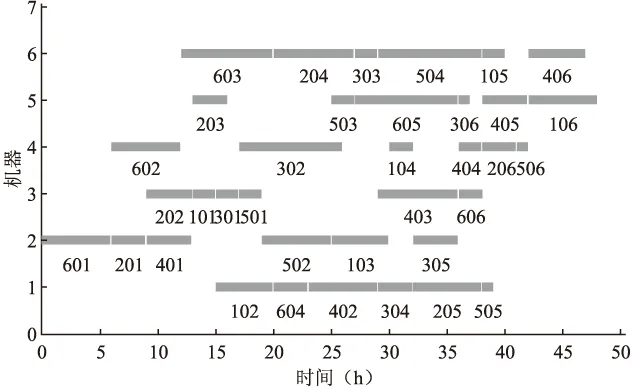
图2 传统PSO-GA算法对应甘特图

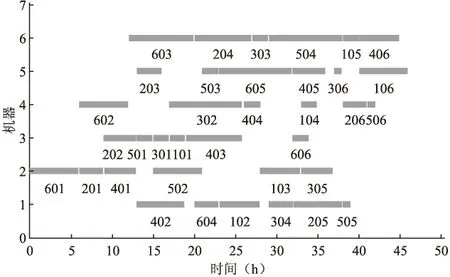
图3 SA-PSO-GA算法对应甘特图

通过图2和图3可以看出，传统PSO-GA算法甘特图排产结果显示48个小时可完成6个工件的生产，GA-PSO-SA算法甘特图排产结果显示46个小时即可完成生产任务，说明GA-PSO-SA算法排产实际效果优于传统PSO-GA算法.两种算法的进化曲线图如图4所示.

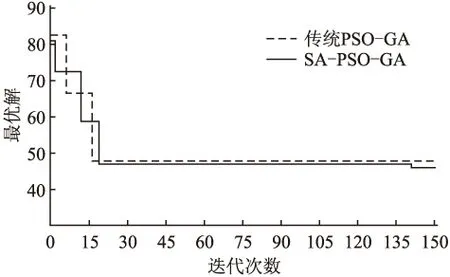
图4 进化曲线图

从进化曲线图可以看出传统PSO-GA算法陷于局部最优，所输出的最优解并不是实际的最优解.并且运行结果显示传统PSO-GA算法运算时间一般为24-20S，SA-PSO-GA运算时间一般为19-16S.SA-PSO-GA算法达到预期效果，优于传统PSO-GA算法.

7 结 语

本文通过对通过对柔性流水车间调度的分析和模型的建立后，提出了一种新的SA-PSO-GA算法.SA-PSO-GA算法在迭代前期继承GA算法前期搜索效率高的特点，在中期继承PSO算法精度、搜索效率高的特点，在后期继承SA算法的概率突跳性跳出局部极值的特点，最终达到快速、高效地得到全局最优解的要求.通过实验仿真比较，验证了SA-PSO-GA算法的优势.