十六烷-水乳液界面电位极大值的理论计算

杨方源， 吴 豪， 朱源哲， 祖力胡马·吾买尔， 余舒锦

(新疆农业大学 数理学院， 乌鲁木齐 830052)

1引 言

界面上的分子电势和其相应的分子结构是影响界面行为的重要因素，其中的电荷相互作用是一种重要的相互作用[1, 2]. 电荷相互作用被认为是分子与分子之间、分子与静电场之间的相互作用，这种相互作用来自于外界或者不稳定的界面离子分布比如界面的双电层结构[3]. 为了探测界面的分子行为，常用的探测手段有：化学滴定法[4, 5]，界面张力法[6, 7]，表面/界面电势法[8-10]，布鲁斯特角成像法[8, 11, 12]，电子顺磁共振法[13]，中子反射法[14]，以及二阶非线性光谱方法[7, 15-21]等.

众所周知，界面上的分子所带电荷很容易通过测量界面的电迁移率[22-26]、测量界面的电流或者电势[9]从而得到其相应的Zeta电位值，从得到的Zeta电位值就可以转化为界面的电荷信息. 理论上，Zeta电位值基于估衣-查普曼(Gouy-Chapman)理论的Graham方程表达如下[3, 27]：

(1)

界面电荷密度Γ或σ是Zeta电位ζ和体系总离子强度浓度I的函数，e是基元电荷，εr是溶剂的相对介电常数，ε0是真空介电常数，kT是热力学能量，z是离子价态. 根据Graham方程可知，一般情况下，当界面有特定的离子时，Zeta电位随着离子强度的增加呈下降趋势. 然而，有研究报道证明电迁移率随着离子强度有极大值的出现，根据Henry方程[28, 29]，由于离子表面的Zeta电位与电迁移率是呈正比的，因此电位也会伴随有极大值的趋势出现，对于电位极大值的出现已经有实验和理论工作进行了报道[30-34]. 到目前为止，对于这一极大值出现的原因解释有三个主流的观点，一是界面上的特异性离子吸附[22, 26, 31, 33]；二是毛发层理论[24, 26, 32-34]；三是界面电导率的反常效应[35]. 然而在特殊的情况下，许多因素都应该考虑，例如，界面电导率的反常现象可以解释界面双电层上的斯特恩层上的离子吸附效应. 在Vanderput等人[31]的文献报道中，毛发层的形成和导致的电导率的变化被用来理解表面覆盖聚苯乙烯颗粒的流动电流和电势. 共离子吸附模型[36]认为电迁移率出现极大值的原因是由于共离子与界面区域的离子有竞争作用，因此导致压缩双电层所致.

其中毛发层理论[37]也是被众人所熟知的一种用来解释电位极大值出现的理论，毛发层理论认为有一层流动的聚合物链在聚苯乙烯颗粒物的表面，由于颗粒表面与离子头基之间的排斥作用，尾链伸入溶液的距离受到体系离子强度、pH值等因素影响. 低浓度时，尾链通过移动滑移面的距离来降低迁移率，这就导致降低了滑移面上电势，也就是Zeta电位，随着体系盐浓度的增加，毛发层逐渐坍塌至表面从而缩短了滑移面与表面之间的距离，这就导致迁移率上升；在更高浓度的情况下，又回归至经典模型，电解质浓度增加导致静电屏蔽效应增强，从而电位下降.

Antonietti等人[38]也报道了不同的实验结果，聚苯乙烯胶体粒子的电迁移率和Zeta电位随着体系离子强度(KCl)的变化，借助O’Brien-White公式[39]理论联系的电迁移率和电位之间关系，转换为电迁移率与体系离子强度之间的关系. 他们的实验结果表明，通过O’Brien-White方法从电迁移率反推计算出来的Zeta电位曲线并没有极大值的出现，尽管其电迁移率的曲线有极大值. 这一结果表明了电迁移率的极大值现象实际上并不是反常的. 在随后的实验报道中，Folkersma等人[24]指出尽管利用O’Brien-White方法，计算出来的电位曲线随着离子强度的变化仍有极大值出现，但是这一极大值现象并不明显. 因此，关于电位会出现极大值现象，人们秉持怀疑的态度. 到目前为止，关于电荷，Zeta电位以及电迁移率随着离子强度的变化问题都是胶体领域和界面研究领域的热点话题.

在本文中，我们利用理论计算的方法研究了十六烷乳液界面电位和电迁移率之间的关系，利用O’Brien-White公式，通过测量得到的电迁移率值反推公式得到相应的Zeta电位值，计算结果表明 Zeta电位曲线规律随着体系离子强度变化是由系统参数决定的. 进一步地，我们分析十六烷乳液表面油滴的电迁移率和电位随着pH值和表面活性剂SDS浓度的变化规律，得出十六烷乳液界面电位是否出现极大值依赖于系统参数的选择.

2实验部分

2.1实验材料

去离子水经超纯水机(Water Purifier, WP-UP-UV-20，四川沃特尔水处理设备有限公司)制备，电阻率为18.25 MΩ·cm.

十六烷(99%, Sigma-Aldrich)用碱性氧化铝(100-200目，阿拉丁)过滤六次，具体步骤参照文献[21, 40]：将100 g碱性氧化铝均匀装入500 mL容量的具砂板存储球层析柱中，约柱型体积的一半，先用75 mL十六烷润洗柱子，然后将十六烷(1 L)倒入柱中，在过滤过程中十六烷流速约2 mL/min，收集过滤后的样品，为纯化一次的十六烷. 之后用纯化一次的十六烷(75 mL)润洗一根新的碱性氧化铝柱层析柱，用同样方法过滤得到纯化两次的十六烷. 以此类推，一共纯化六次，最终1 L十六烷经六次纯化后减少到约600 mL，之后用于实验.

十二烷基硫酸钠(SDS，99%, Sigma-Aldrich)用无水乙醇(99.7%，天津百世化工有限公司)和水的混合溶剂(V:V=95:5)重结晶三次，去除杂质, 这些杂质的存在，对其溶液的临界胶束浓度(CMC),表面张力，表面粘度，以及其他物理性能都有着很大的影响[41]. 具体纯化步骤为：5 g SDS加入50 mL醇/水混合液中，然后在磁力搅拌下使用冷却回流装置加热至80℃，直至SDS完全溶解，室温下冷却结晶，抽滤干燥，如此过程重复三次，SDS分子结构式如图1所示.

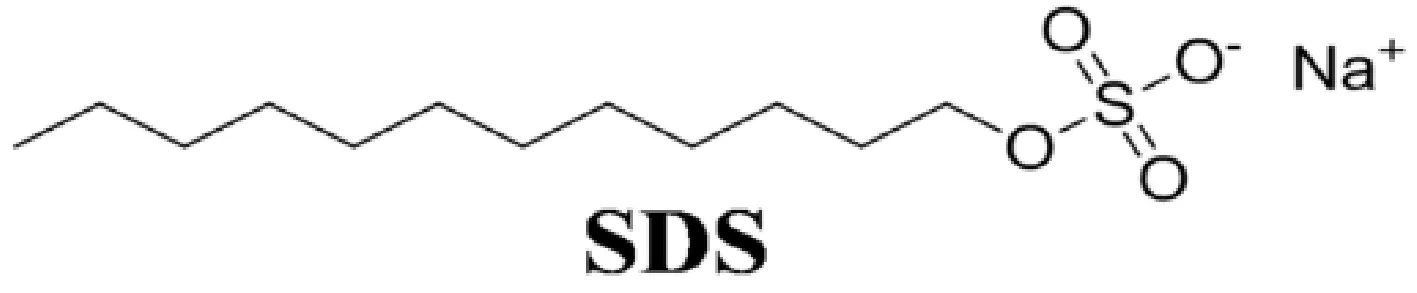
图1 SDS分子结构式.Fig. 1 Molecular structure of the SDS surfactant.

氢氧化钠 (NaOH, 99.99%, Sigma Aldrich)和盐酸(AR reagent, 37% solution in water, Tianjin Baishi Chemical Co. Ltd, China)用于调节乳液的PH值.

氯化钠 (NaCl, >99 %, Sigma Aldrich)高温500 ℃灼烧至10个小时以去除杂质，溶于水然后通过0.025um口径的滤膜(Merck Millipore Ltd.)过滤两次以去除不溶性的杂质.

实验中用到的玻璃器皿用食人鱼洗液(H2O2: H2SO4体积比为 3:7)浸泡，用于去除残余有机物，之后洗净晾干待用. (注意：食人鱼液具有强氧化性使时要慎重).

2.2乳液制备和稳定性测试

无表面活性剂的乳液的制备过程：将纯的十六烷和DI水按体积比为1:50混合，首先通过均质仪(Omni, TM125-220, 8000 rpm)混合约1分钟，接着在25±3℃恒温水浴中磁力搅拌(500 rpm)15 min，然后在25± 3℃恒温水浴中超声(KQ-300DE, 300 W, 40 kHz,昆山超声有限公司)10 min从而形成稳定的乳液. 待乳液静置至常温，将制备好的乳液溶液稀释100倍用于测试. 利用动态光散射仪，将制备好的无表面活性剂乳液进行粒径的测试，粒径为200nm-300nm左右，并且粒径能够稳定在6个小时的时间内(其粒径分布图及制备好的乳液照片如图2所示). 实验中在制备好的乳液中加入酸、碱或阴离子表面活性剂，实验中所需的 pH值均通过pH计(Mettler Toledo, PE20K, 电极：LE438)进行调节. 用HCl溶液将乳液调为pH=5后继续加入HCl用pH计将乳液调为pH=2、3和4，加NaOH用pH计将乳液调为pH=6、7、8、9、10、11、12和13，之后分别测它们的电迁移率.

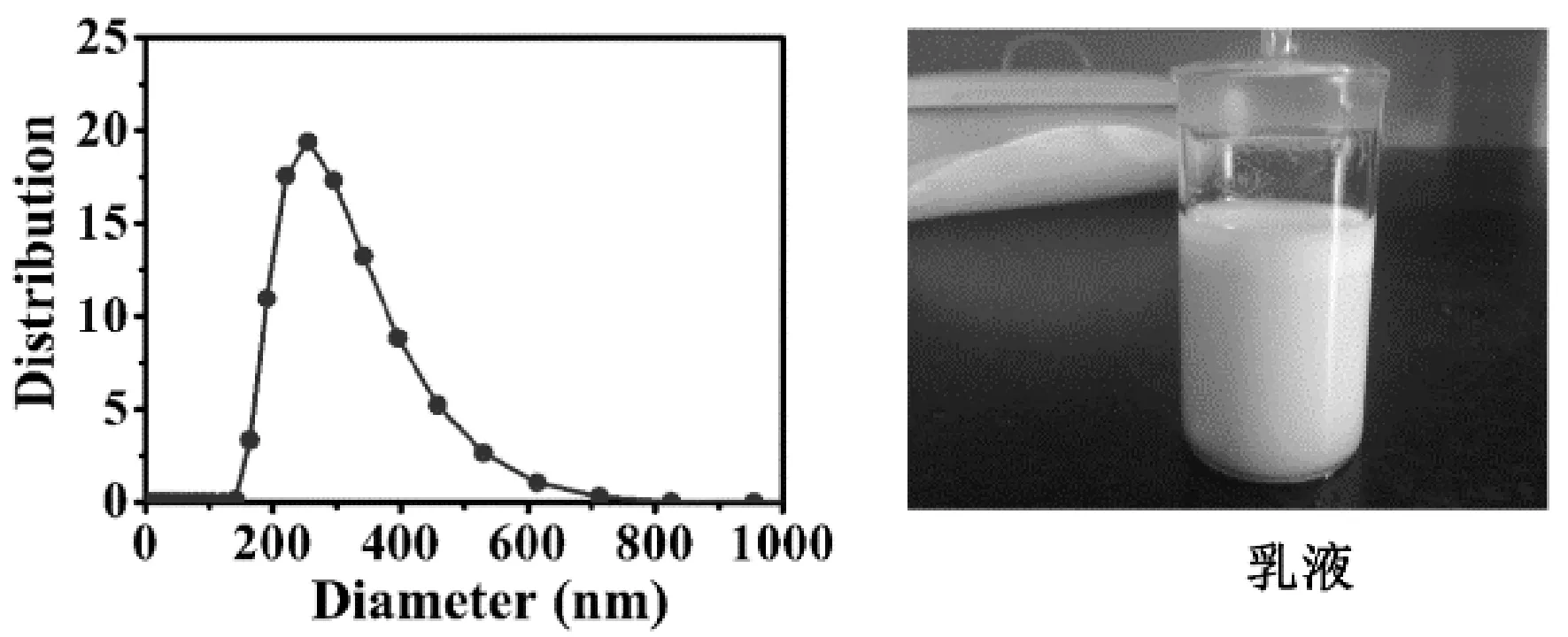
图2 乳液粒径分布图(左)及乳液照片(右).Fig 2 The number distribution of the droplet size in the hexadecane-water emulsions prepared with the protocol described in the text (left) and the picture of the emulsion (right).

2.3电泳测量

电迁移率和乳液粒径测试使用动态光散射仪器(DLS，ZS90，Malvern). 检测样品的示意图如图3所示. 测试过程激光波长为633 nm，测量角度为90°，测试温度设定为25℃. 油滴的平均粒径在特定的环境下保持相对稳定并且粒径的偏差不超过10%. 同时，在本实验中，乳液中加入了酸、碱以及阴离子表面活性剂，因此测得的油滴半径范围在80nm-300nm之间，但是在同一离子强度下，粒径保持不变或者偏差不超过10%. 实验中通过电位仪，我们首先纪录的是电迁移率的值，因为电位仪采用的是电泳测试的方法，所以直观的数据是电迁移率的值，然后通过O’Brein-White公式反推得到相应的Zeta电位的数值. 实验数据采用三次测量后的平均值.

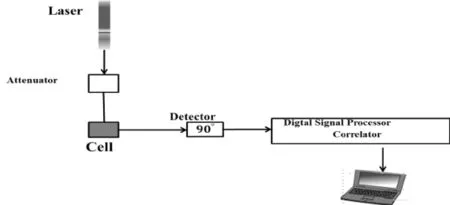
图3 电位测量示意图.Fig 3. The schematic diagram of Zeta potential measurement.

3结果与讨论

3.1Zeta电位值与电迁移率值之间的关系

通常认为Zeta电位和电迁移率之间的关系由Henry 方程来描述. 基于Smoluchowski[42]公式和Hückel[43]公式，Henry[28]提出了电迁移率的方程，此方程适用于较低的ζ和任意的ka值，表达式为：

(2)

f(κa)=1-eκa{5E7(κa)-2E5(κa)}

(3)

其中En(κa)是n阶积分项，f(κa)是Henry函数. 当κa→，f(κa)→1，公式(2)近于Smoluchowski公式，而当κa→0，于是f(κa)→2/3且公式(2)变为Hückel公式.

Henry公式认为球形粒子周围的电势分布是均一的，然而对于处在较高电势下的粒子，其双电层并不是对称的，这种使得电势分布不对称的效应一般称为弛豫效应. Henry方程并未考虑此弛豫效应，因此也就只适用于低阶的Zeta电位. Henry方程在表达电位和电迁移率之间的关系时有其局限性，能够完整表达电迁移率的式子随后由Overbeek和Booth[44]提出，他们给出了电迁移率在任意电位值下的表达式. Loeb和Overbeek[45]利用计算机得出了电迁移率和电位公式的数值解. O’Brein和White在1978年发展了这种计算机模拟的方法，得到了公式的精确解. O’Brein和White推导电迁移率和电位之间的关系具体步骤如下：

(4)

(5)

通过O’Brien公式(6)得到准确的电迁移率的值：

(6)

其中，

(7)

(8)

(9)

m±代表溶液中正负离子的迁移率. 这里，不同离子的迁移率可以从稀溶液中极限摩尔电导率求得.

为了得到电迁移率推导到电位的普适规律，我们对电迁移率和电位之间的关系进行了计算模拟，如图4所示.

从图中可以看出，从电迁移率推导至的电位曲线有两条，除了个别电迁移率的点以外，其他一个电迁移率值均对应两个Zeta电位值的点. 其中两条电位图中的点线图表示电位值较大，其没有物理意义并在以往的报道中并未进行阐释. 基于此原因，我们只关注合理的那条曲线(即实线图). 在图4(a)中，可以看出电迁移率随着体系离子强度的增加有个极大值的出现，然而根据公式反推至的电位曲线随着离子强度的增加是单调下降的，这一趋势符合Gouy-Chapman模型和以往人们报道的结果[43]. 在图4(b)和(c)中，选用的粒子尺寸从150nm变为250nm，盐的类型从NaCl变为KCl，这时不仅电迁移率随着离子强度有极大值，由电迁移率推导至的电位值随着离子强度的增加也有极大值的出现. 从图4(d)中发现降低电迁移率的数值，得到的电位曲线仍有类似(b)和(c)的曲线变化趋势.

从以上的计算结果可以看出，根据O’Brien-White公式从电迁移率反推得到的电位随着离子强度变化的曲线，其曲线的变化趋势依赖于所选体系，Zeta电位是否有极大值的出现依赖于体系参数的选择.

3.2十六烷乳液Zeta电位在不同的pH值和SDS浓度下随离子强度的变化

研究乳液表面的电位变化情况对于理解界面的分子行为有重要的作用，实验中我们首先通过电位测量仪直接得出乳液电迁移率随体系离子强度的变化情况，再通过O’Brien-White公式反推出相应的电位值，通过结合理论计算和实验手段来进一步理解乳液表面的带电信息. 这里，主要选取pH=7和pH=11, SDS浓度为50μM和SDS浓度为10mM的情况下，十六烷乳液Zeta电位随着体系离子强度变化的数据点进行分析，这些浓度的选取涵盖了较低的浓度范围(pH=7 和50 μM SDS)和较高的浓度范围(pH=11 和10 mM SDS). 依据O’Brien-White公式成立的极限条件ka≥10，我们这里选取NaCl的浓度大于等于100μM, 如此就能保证公式中的ka接近于10. 其中SDS浓度的选取，避开了其临界胶束浓度的点，已有文献证明，SDS的临界胶束浓度会随着体系离子强度的增加发生变化[46]，因此这里选取的浓度都远离了其临界胶束浓度. 实验结果将通过电位测量仪直接测得的电迁移率的曲线与通过公式反推得到的真实的电位曲线进行比较. 通过上一部分的描述我们已经知道，实际上一个电迁移率的值对应着两个电位值，在这里我们只保留了一组电位曲线，这是因为我们去除了结果中得到的那条没有物理意义的曲线.

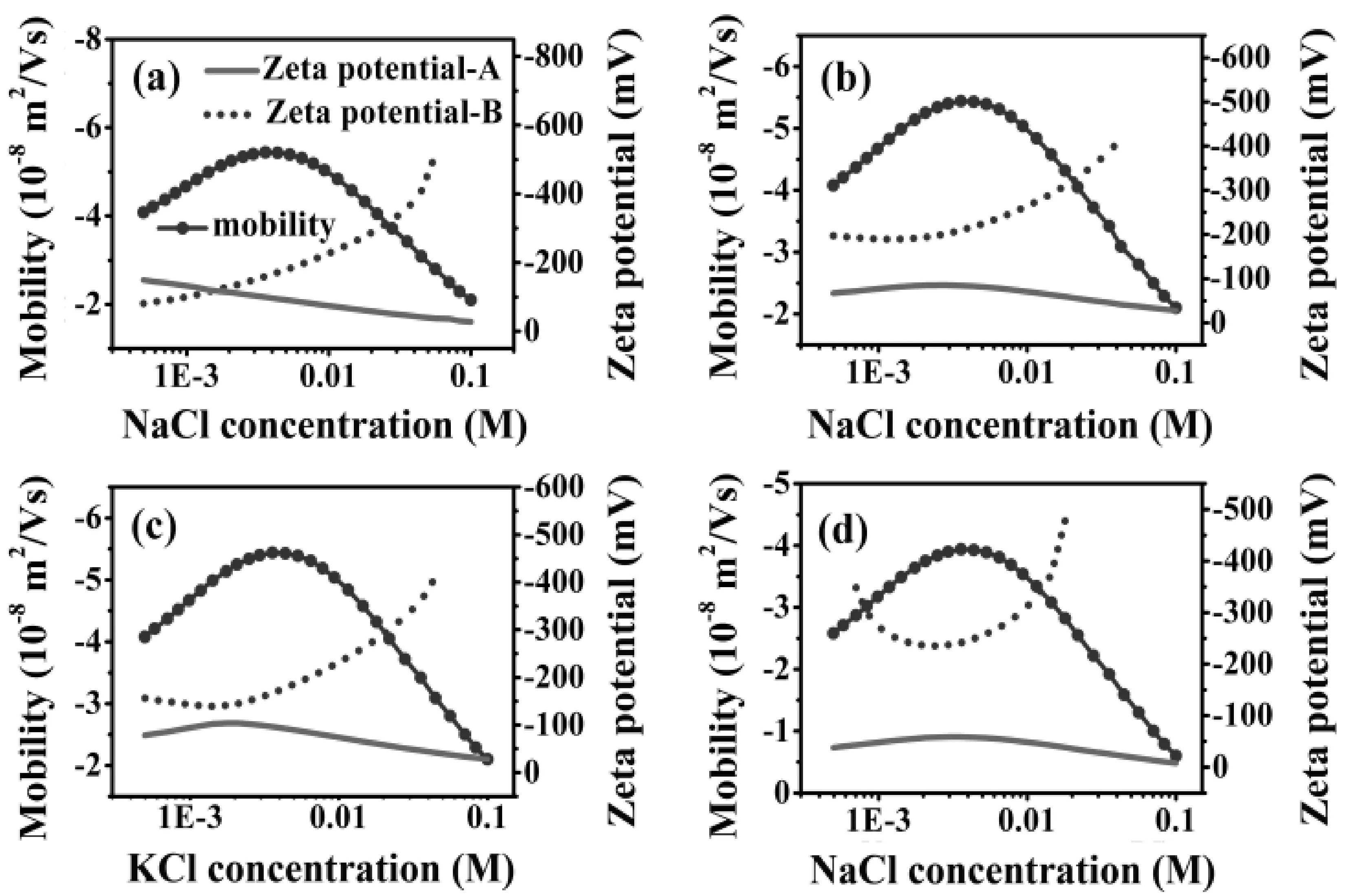
图4 从电迁移率值计算得到电位值. 对于 (a) 和 (d), 粒子半径a=150 nm,电解质类型是 NaCl. 对于(b), a=250 nm, 电解质类型是NaCl. 对于(c), a=150 nm, 电解质类型是KCl.Fig. 4 Calculated zeta potential curves (solid lines and dotted lines) from the ionic strength dependent electrophoretic mobility curves with a maximum (solid circles with lines). For(a) and (d), the radius of colloidal particles a=150 nm, the electrolyte type is NaCl. For (b), a=250 nm, the electrolyte type is NaCl. For (c), a=150 nm, the electrolyte type is KCl.

其中具体的电迁移率的值和由O’Brien公式进行反推得到的Zeta电位的值如下列各表所示，具体的推导公式也在上面的理论部分进行过推导，电迁移率与电位之间的关系如公式(6)所示，在这里不做重复推导，只给出电位和归一电位之间的关系，如下所示：

(10)

通过计算结果发现，并不是所有的电迁移率的值都有对应的两个电位值，有的点只有一个电位值与电迁移率的值对应，这可能与我们选取的体系有关.

通过测量得到的电迁移率的值以及公式反推得到其相应的电位值，实验结果和计算结果如图5所示，图中(a), (b), (d)中的电位值和电迁移率的值都随着体系盐浓度的增加呈现单调下降的趋势，而(c)图中的电位值和电迁移率的值出现了极大值. 通过分析发现(b), (d)分别对应的是pH=11和SDS=10mM浓度这两个点，这两个浓度下吸附都分别达到了其饱和吸附. 而(a)图中通过公式反推计算得到的电位值也并未出现极大值，分析原因是由于随着体系盐浓度的增加Na+浓度随之增加，因为体系的pH=7, 乳液表面吸附OH-的量并未超过其吸附Na+的量. 因此这三个浓度下电位均为出现极大值现象. (c)图中在SDS=50μM的浓度下，计算得到电位值出现了极大值的现象，乳液电位会随着离子强度的增加出现极大值，这是因为随着NaCl浓度的增加，Na+的增多会促进界面吸附更多的阴离子也就是DS-离子，那么使得乳液表面的电位逐渐增大，DS-离子的逐渐增加也会反过来导致表面活性剂分子(SDS)在乳液表面排列的更加有序，从而促进DS-在乳液表面的吸附，这时电位值达到最大，出现一个极大值的现象，然而当NaCl浓度过高时，电位反而下降，这是因为DS-与Na+之间很强的电荷作用，从而导致净电荷下降，针对这一情况也有不同的结构模型来解释[47]，表面活性剂在水油界面吸附电位出现极大值现象有助于我们理解水油界面上的分子结构和其排列行为.

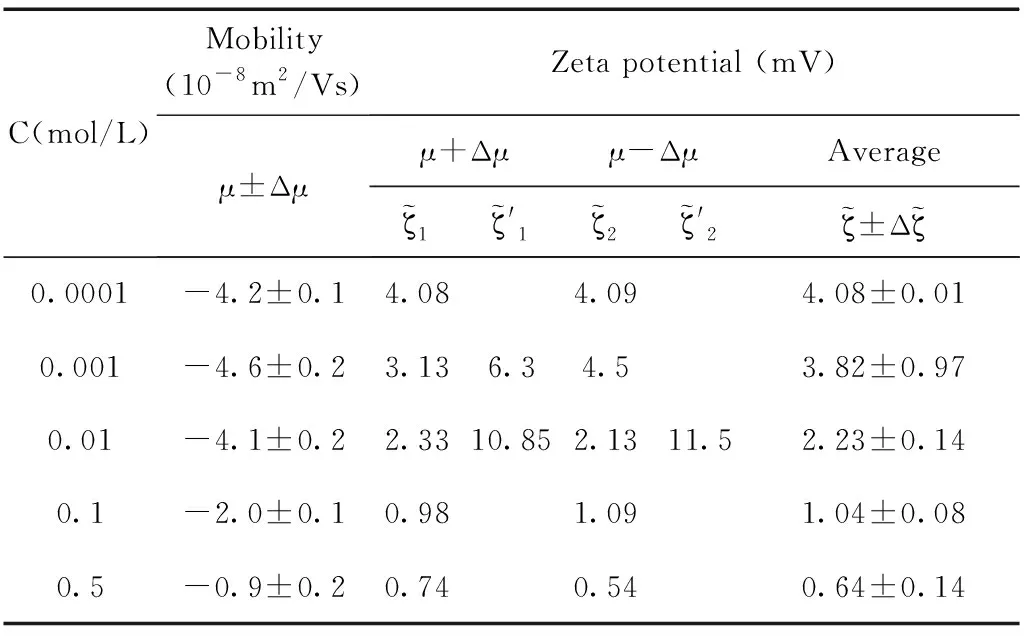
表1 乳液pH=7，电迁移率值与通过O’Brien公式计算得到的电位值.

图5 乳液的电迁移率(圆点)和推导得到的Zeta电位值(方块). (a) pH=7, (b) pH=11, (c) SDS=50uM, (d) SDS=10mM.Fig. 5 Converted ionic strength dependent zeta potential curves (empty squares) from the electrophoretic mobility curves (solid circles) measured in the hexadecane-water emulsions at pH 7 (a) and pH 11 (b), and the hexadecane-water emulsions in the presence of SDS at concentration of 50 μM (c) and 10 mM (d), respectively.

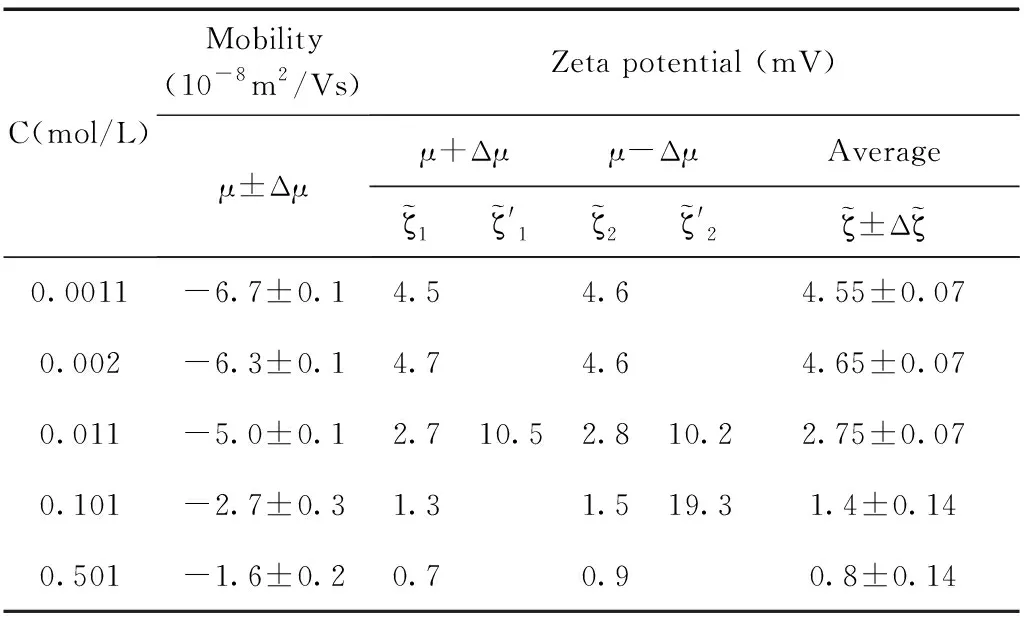
表2 乳液pH=11，电迁移率值与通过O’Brien公式计算得到的电位值.

表3 乳液SDS=50uM，电迁移率值与通过O’Brien公式计算得到的电位值.

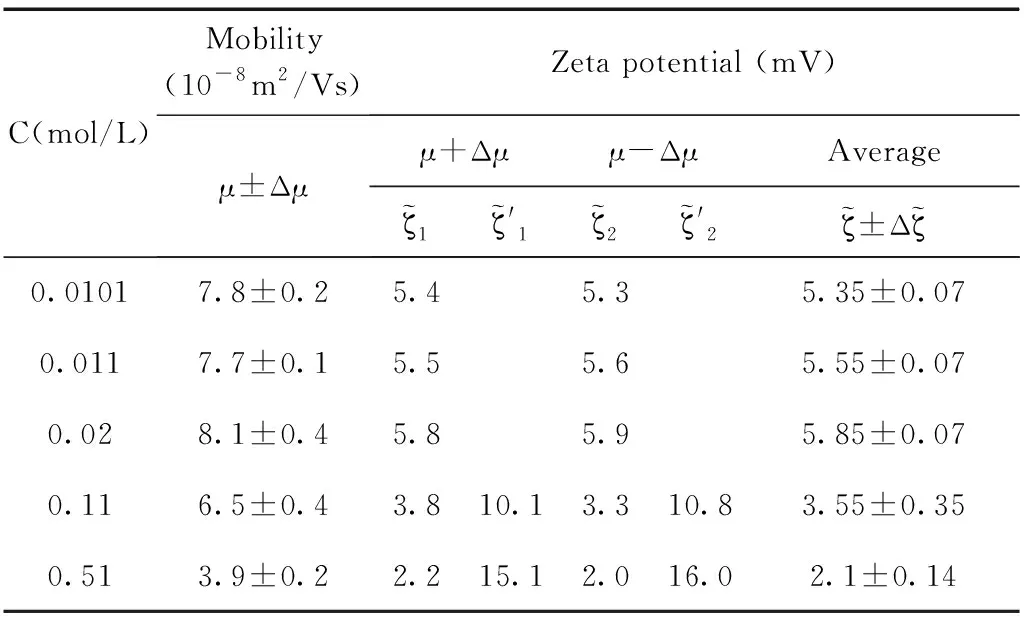
表4 乳液SDS=10mM，电迁移率值与通过O’Brien公式计算得到的电位值.

4小 结

本章借助O’Brien-White和估衣-查普曼理论，想到了从电迁移率值反推电位值这一转换关系，通过O’Brien-White公式从理论上推导出乳液电位随着体系离子强度的变化规律，从电迁移率的值与电位值之间的关系得出，一个电迁移率的值对应着两个电位值，也就是说电迁移率和电位之间的关系不是一一对应的，在计算了大量的数据后，进行分析，得知其中有一条电位曲线是不符合物理意义的，所以经过筛选留下有物理意义的那条曲线. 其次，通过分析实验测得的十六烷乳液电迁移率和电位随着体系离子强度的曲线变化，可以得知电位是否出现极大值依赖于系统参数的选取，例如电迁移率数值的大小，体系电解质种类的选择，以及离子半径的大小等，这些参数的不同都会影响电位是否出现极大值这一现象.