基于集成学习算法的航路网络航段交通拥挤识别方法研究

李桂毅，郭铭宇，罗一帆

(南京航空航天大学a.民航/飞行学院；b.航空学院，南京211106)

0 引言

航路网络交通拥挤带来的航班延误直接影响空中交通运行安全与效率.传统解决空中交通拥挤的方法主要是控制起飞时间或飞行间隔，其决策缺乏精确的交通态势信息支持，效果欠佳.如何快速、精准地识别航路网络交通拥挤状态与节点，进而制定交通拥挤的管控策略已成为重要研究课题.

在空中交通领域，徐肖豪[1]提出了基于FCM(Fuzzy C-means Clustering)算法的终端区交通拥挤状态评价方法，Jiang[2]基于复杂网络构建了空中交通拥挤识别模型，李善梅[3]提出了基于灰色聚类算法的交叉航路拥挤识别模型，张兆宁[4]提出了交通拥挤判定方法及不同交通状态下交通流参数阈值区间，李桂毅[5]等提出了基于FCM与粗糙集理论的多扇区交通拥挤识别模型；在地面交通领域，Eleonora[6]提出了基于车辆或驾驶员手机GPS数据的道路交通拥挤探测方法，Felix[7]提出了基于浮动车数据和时空聚类算法的地面路网交通拥挤识别方法，Wang[8]建立了基于神经网络的道路通行时间预测模型，预测路网交通拥挤状态，董春娇[9]基于交通流率、速度和占有率等参数和SVM算法建立了城市快速路网交通状态的判别模型，Kumar[10]基于人工神经网络模型实现城市高速公路交通流参数的短时预测.以上成果为航路网络交通拥挤识别研究奠定了较好基础.

航路网络交通易受恶劣天气、军航活动等诸多因素影响，具有非线性、多变性、复杂性等特征.机器学习处理大样本数据能力强，较适用于拟合非线性复杂函数，具有良好的泛化能力.集成学习算法通过构建多个基学习器可提升机器学习效果,提高识别精度,在城市道路交通拥挤预测、城市人流行为分析方面得到成功应用[11-12].本文基于集成学习算法构建航路网络交通拥挤识别模型，识别路网航段交通拥挤状态.

1 航路网络交通拥挤识别思路和框架

航路网络交通拥挤识别的总体思路为基于路网航迹数据，构建航段交通拥挤评价指标，结合FCM和集成学习算法构建路网航段交通拥挤等级划分与识别模型，实现航段交通拥挤识别.具体流程如下：

(1)选定航路网络区域范围，采集ADS-B航迹数据，统计航路网络交通流参数；

(2)建立路网航段交通拥挤评价指标，涵盖交通流量、交通密度、交通接近率、交通饱和度，结合航迹数据计算评价指标值；

(3)构建基于路网航段FCM交通拥挤划分模型，聚类划分路网航段交通拥挤等级；

(4)构建路网航段集成学习交通拥挤识别模型，基于路网交通拥挤评价指标和拥挤等级数据完成模型训练，识别航段交通拥挤状态.

图1为航路网络航段交通拥挤识别总体框架.

图1 航路网络航段交通拥挤状态识别总体框架Fig.1 Overall framework of air traffic congestion identification in air route network segment

2 航路网络交通拥挤状态划分方法

2.1 航路网络航段交通拥挤评价指标

分别从路网航段交通流量、交通密度、交通饱和度、交通接近率4个指标维度评价路网航段交通拥挤等级.指标定义如下.

(1)航段交通流量.路网航段断面单位时间内通过的航空器的架次数，反映路网内部交通的流动负荷.

(2)航段交通密度.路网中航段单位长度内单位时间内航空器的架次数，反映路网内部航段飞行密集程度.

(3)航段交通饱和度.路网某航段单位时间内交通量同容量限制阈值的比值，用于度量航段交通负荷强度.

(4)航段交通接近率.路网中某航段单位时间内航空器之间的接近程度，反映航段交通分布的密集特性.依据我国空管法规，雷达管制条件下航空器之间最小安全间隔距离为水平方向10 km或垂直方向300 m，至少满足其一，否则构成不安全事件.基于椭球面计算航空器间的相对间距，负指数函数计算航段交通接近率.当航段内航空器相对距离接近1时，航空器相对间隔接近最低安全间隔，航段交通接近率就越大，管制员需要较多精力监视和调配飞行冲突，航段交通状态表现越拥挤；当航段内航空器相对距离越大，航段交通接近率也就越小，交通拥挤程度也就越低.

式中：dij为航空器i与j之间的空间相对距离；,为航空器i与j的位置向量；SH,SV分别为航段最小水平间隔距离和最小垂直间隔距离，分别取10 km和300 m；(xi,xj),(yi,yj)分别为航空器i与j的坐标值；(zi,zj)为航空器i与j的飞行高度；Pd为航段交通接近度；Pseg为航段交通接近率；n为航段内航空器数量.

图2为我国某航段交通接近率和交通流量变化趋势，可知航段交通接近率同其交通流量的总体变化趋势基本一致，能够从交通分布均匀性维度反映交通拥挤程度.

图2 我国某航段交通接近率和交通流量的变化趋势Fig.2 Trend of traffic approaching rate and traffic flow in an air route of China

2.2 航路网络航段交通拥挤划分模型

FCM算法属于无监督学习算法，适用于模糊、无清晰界限的交通拥挤状态的划分.假定航段交通拥挤评价指标矩阵为X，即

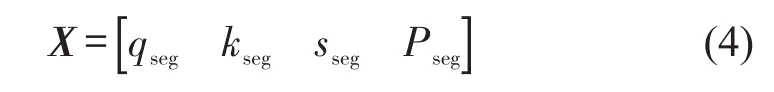
式中：qseg为航段交通流量；kseg为航段交通密度；sseg为航段交通饱和度；Pseg为航段交通接近率.

基于FCM算法对矩阵X在一定时间内的历史数据进行聚类分析，确定最佳的聚类划分类别数，明确航段交通拥挤等级划分.将X聚类划分为β个簇，交通拥挤状态划分算法为

式中：Jα(∙)为FCM算法的目标函数；U是每个聚类样本数据与相应聚类簇的隶属度；l为聚类数据样本序号；c为聚类数据样本数量；x为聚类划分簇的序号；μxl为第l个聚类数据样本属于第x个聚类簇的隶属度，μxl∈[0,1]；dxl为第l个聚类数据样本到第x个聚类簇的欧式距离；α为加权指数，其值越大，聚类模糊性越强.

基于肘部法则确定最佳聚类簇数，即拥挤等级数.肘部法则通过计算聚类簇内误差平方和(ESSE)确定最佳划分簇数，即

式中：Cx为聚类划分的第x个簇；p为Cx中的样本点；mx为Cx中的所有样本点的质心；k为聚类划分的簇数.

从小到大设定不同的簇数进行聚类分析，计算ESSE值.随着聚类簇数的增多，各簇内样本数量会越来越少，样本点距离聚类中心的距离也越来越近，ESSE值随划分簇数增多而减少.当划分类别数小于最佳簇数时，类别数增加会大幅增加每个簇的聚合程度，ESSE值下降幅度会很大.当划分簇数到达最佳簇数时，再增加簇数，每个簇的聚合程度增幅会迅速变小，ESSE值下降幅度会趋于平缓，进而形成一个拐点，拐点对应的划分簇数，即为最佳划分簇数.

3 航路网络交通拥挤状态识别方法

3.1 航段交通拥挤状态识别模型

集成学习算法原理是构建一系列基学习器对训练样本学习，挖掘训练样本的内部规律，并使用集成算法把各基学习器学习结果整合起来，从而获得比单学习器模型更好的学习效果，算法原理如图3所示.

图3 路网航段交通拥挤状态集成学习识别原理Fig.3 Principle of ensemble learning identification for traffic congestion in air route network segment

集成学习识别模型可采用决策树或k近邻算法构建基学习器，集成学习算法采用Bagging算法，结合算法采用Stacking学习法，如图4所示.基于交通拥挤评价指标和拥挤等级数据训练模型，结合指标数据进行交通拥挤等级识别.

图4 路网航段交通拥挤集成学习识别模型结构Fig.4 Structure of ensemble learning identification model for traffic congestion in air route network segment

3.2 Bagging学习策略和Stacking结合策略

Bagging学习策略重复产生样本作为训练样本集，从大小为n的原始训练样本集中随机地抽取m个样本作为每次训练的样本集，训练相互独立的基学习器，完成基学习器的集成.首先，对原始训练样本集进行有放回的抽样；然后，针对同一原始训练样本集，每次从中随机抽取相同数量的训练样本子集训练一个基学习器；最后，集成训练好的基学习器，如表1所示.

基学习器结合策略是指将训练好的基学习器输出结合起来的方法，如Stacking结合算法，其原理为使用另外一个学习算法将基学习器的结果结合在一起.首先，基于初始训练样本集训练生成各基学习器；然后，将各基学习器的输出作为新的训练样本集，初始训练样本集训练样本标记仍作为样本标记，生成Stacking学习器；最后，将训练好的Stacking学习器结合各基学习器输出，结合成集成学习模型.

表1 Bagging集成算法Table 1 Bagging ensemble algorithms

4 实证分析

如图 5所示，选取我国 A599、R343、R474、R399、B330航路共9条航段组成的航路网络进行航段交通拥挤识别验证分析.实验数据为2018年3月1～14日路网ADS-B数据.拥挤指标为14 d，共10 296组，时间间隔为15 min.

图5 实验航路网络结构Fig.5 Experimental air route network architecture

(1)确定航段交通拥挤最佳划分等级数.

对14 d拥挤指标数据进行聚类分析，划分类别数k分别取1～9.图6给出了k值与ESSE值的关系：k=1～4，ESSE值下降很快；当k=4之后，ESSE值下降趋于平缓.可知最佳划分拥挤等级数为4，对应为严重拥挤、轻度拥挤、畅通、非常畅通.

图6 航段交通拥挤指标聚类手肘分析拐点图Fig.6 Air route traffic congestion index cluster elbow analysis inflection point diagram

(2)进行航段交通拥挤等级聚类划分.

对14 d拥挤指标数据进行聚类分析，拥挤等级数为4，指标数据标准化后的聚类结果如图7所示，分别从流量—密度、流量—接近度、流量—饱和度、密度—接近度、密度—饱和度、接近度—饱和度6个维度展现聚类结果，进而完成航段交通拥挤等级的划分.

图7 路网航段交通拥挤指标聚类结果Fig.7 Clustering results of traffic congestion indicators in air route network segment

(3)进行集成学习识别模型参数设定.

模型参数共有5种设定，如表2所示，验证模型不同基学习器设置的识别性能.训练数据为3月1～4日共3 456组指标和对应的拥挤等级数据，其中80%为训练样本，20%为测试样本.

表2 路网航段交通拥挤识别模型参数设定Table 2 Parameter setting of traffic congestion identification model for air route network segment

模型识别性能评价指标如下.

①识别准确率.

②平均绝对误差.

③最大绝对误差.

④均方根误差.

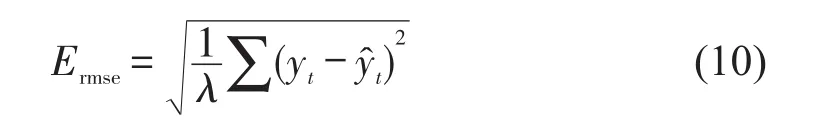
式中：λacc为交通拥挤识别正确的样本数；λ为拥挤识别总样本数；yt为拥挤等级实测值；为拥挤等级识别值.

表3为在5种参数下，模型识别性能的比较.识别性能依次为 Model 1、Model 2、Model 5、Model 3、Model 4，其中，Model 1识别精度最高为98.34%.可知决策树基学习器识别精度高于k近邻基学习器，Stacking学习集成方法识别精度高于投票法.本文选用决策树基学习器和Stacking结合算法构建集成学习识别模型.

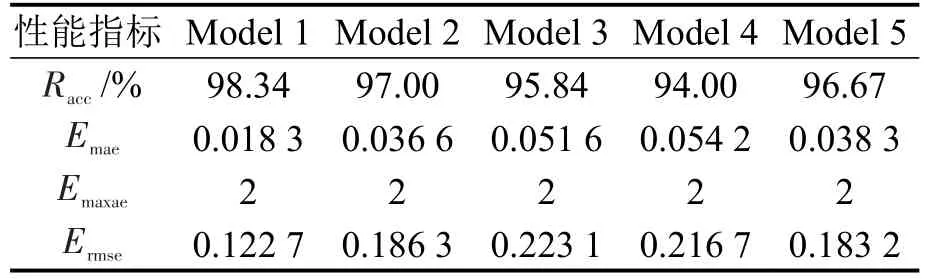
表3 5种设定下的集成学习模型识别性能Table 3 Identification performance of ensemble learning model under five settings

验证基学习器数量对模型识别精度的影响，结果如表4所示.随着基学习器数量增加，准确率逐步增加，误差逐渐减小，当选取9个基学习器时，准确率为98.34%.

表4 不同基学习器数量的集成学习模型识别性能Table 4 Performance of ensemble learning model with different number of base learners

(4)比较分析集成学习模型同其他模型的识别性能.选取BP神经网络识别模型进行比较分析，性能对比如表5所示.可知集成学习模型识别准确率和识别误差均优于BP神经网络模型，故选用集成学习构建识别模型具有一定优势.

表5 集成学习识别模型与BP神经网络识别模型性能对比Table 5 Performance comparison between ensemble learning model and BP neural network model

路网航段3月4日交通拥挤集成学习模型识别结果如图8所示.通过实证分析可知，航段交通拥挤集成学习识别模型能够较好地实现路网航段交通拥挤的识别.

图8 路网航段3月4日的交通拥挤等级集成学习识别结果Fig.8 Ensemble learning identification of traffic congestion level in air route network segment on March 4

5 结论

本文基于集成学习算法提出了航路网络航段交通拥挤识别方法，利用路网航迹数据，建立航段交通拥挤评价指标，实现路网航段交通拥挤综合划分与识别.实证研究表明，路网航段交通拥挤集成学习识别模型的识别准确率可达98.34%，优于BP神经网络识别模型，识别精度较高，识别性能优良，可用于航段交通拥挤识别，为航路网络交通拥挤综合管控提供决策支持.