基于耐受性的城市轨道交通车厢立席密度研究

陈 伟，李宗平*，余大本，鞠艳妮，尹嘉诚

(西南交通大学a.交通运输与物流学院；b.综合交通运输智能化国家地方联合工程实验室；c.综合运输四川省重点实验室，成都610031)

0 引言

随着国民经济的持续快速发展、城市化水平的不断提高，我国城市轨道交通正处于大发展、大建设阶段，随之而来的地铁拥挤也逐渐成为规划建设和运营管理的焦点问题.过度拥挤不但会降低乘客出行的舒适度，还会导致乘客之间发生推搡、踩踏等冲突事件，对乘客的人身安全产生危害[1].因此，开展城市轨道交通车厢立席密度研究，对地铁立席密度标准的优化和地铁运营的改善具有重要意义.

在城市轨道交通中，立席密度的界定和计算方法尚未形成统一标准.《城市轨道交通工程设计规范》(DB11/995-2013)将定员立席密度标准定为4.5～5.0人/m2，《地铁设计规范》(GB 50157-2013)规定在确定系统运能时立席密度按照5.0～6.0人/m2计算，以上规范主要从系统运能和经济成本角度确定立席密度.已有研究中，主要通过研究立席密度与乘客所受到拥挤力的关系[2]，进行车厢立席密度估算.陈锋等[3]通过研究乘客个体空间对不同立席密度进行服务水平分级.卢春霞[4]通过乘客面积投影研究人体安全极限密度.史芮嘉等[5]采用SP调查研究车厢内乘客立席密度及出行距离与乘客在车厢内站立位置选择的影响方式.吴奇兵等[6]利用简化社会力模型对车厢立席乘客空间舒适度进行研究.现有研究方法主要是对车厢拥挤度的静态评价，部分研究对时间因素考虑方面相对单一，没有足够重视不同类型乘客对舒适度期望不同的特点.

本文针对已有车厢立席密度计算方法的缺点，综合考虑时间—空间对乘客舒适度的影响，将区间模糊数引入乘客时间—空间综合耐受感知模型，结合仿真计算结果对立席密度进行修正，确定合理车厢立席密度，避免单一因素对总体目标的过度影响，使计算结果更加科学合理.

1 主要影响因素分析

乘客在使用轨道交通出行过程中，受到车站和线路多个环节的服务，根据乘客属性和环境的不同，乘客对各项服务设施的耐受性表现也会不同.这里的耐受性可以理解为乘客对时间、体力和心理的一种综合忍受过程，这种过程会受到时间、空间等因素的影响.这种叠加并不是简单的加权，而是心理和生理的叠加[7].当乘客在出行过程的综合耐受感知逼近自身可以承受的极限时，生理和心理都会处于崩溃的边缘，带来的出行体验也是极差的.

乘客乘坐轨道交通的服务水平主要表现在车站设施和车厢设施的服务水平，和乘客乘坐体验最为紧密相关的是车厢立席密度，而不同人群、不同出行目的对不同服务水平的耐受性不同.乘客乘坐轨道交通线路，耐受性的主要影响因素有：车厢立席密度、站立时间和候车时间，如图1所示.车厢立席密度、站立时间主要体现了乘客在车厢内的服务水平.研究发现，候车时间对乘客的综合耐受性影响程度不高，但不同类型乘客对候车时间关注的程度差别较大，这为后续研究不同类型乘客所能接受的最大立席密度奠定基础.另外，即使车厢内拥挤程度不高，过长的候车时间也会影响乘客综合耐受感知，乘客对立席密度的期望也会改变，这也是现有研究中容易被忽略的.在交通行为理论研究中，大多数交通行为阈值都设置在其行为样本总量的70%～80%[8].本文结合人体功效学定义，取耐受极限的80%为耐受阈值.

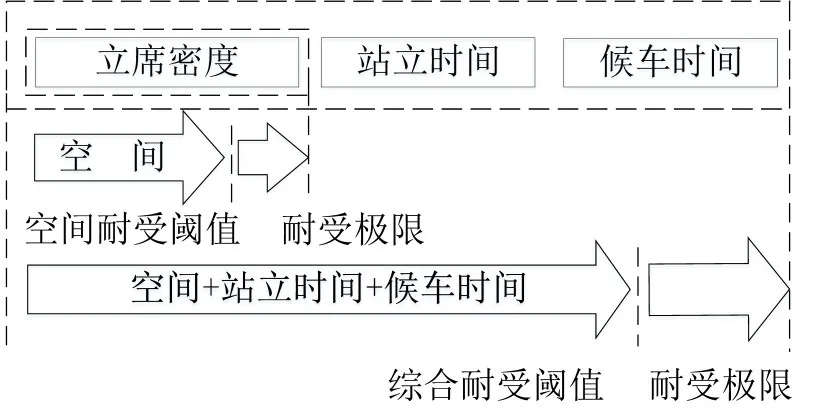
图1 乘客耐受性主要影响因素Fig.1 Main influencing factors of passenger tolerance

2 耐受感知模型

2.1 空间耐受感知模型

结合我国最新行人尺寸标准，考虑不同着装和行李条件下乘客的体宽和体厚增量，按照椭圆形投影，计算得到乘客个体空间占用面积，如表1所示.

分析乘客空间尺寸之后，根据“人体气泡”概念[9]，将车厢立席乘客所占空间进行划分，如图2所示.压缩空间为乘客受到挤压时所占空间，人体正常空间为乘客保持正常站立时所占空间，身体活动空间为乘客需要完成常规活动所占空间，舒适空间为乘客期望与他人保持一定距离所需空间.

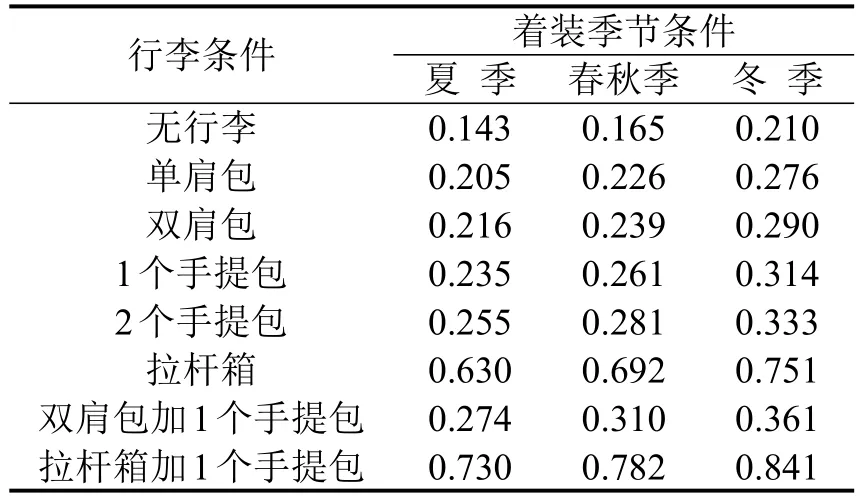
表1 不同着装条件下人体空间尺寸Table 1 Body space size under different dress conditions (m2)

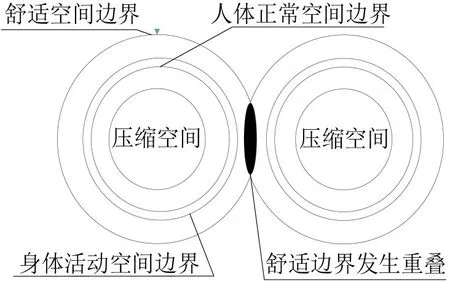
图2 乘客所占空间示意图Fig.2 Schematic diagram of space occupied by passengers

有学者借鉴社会力模型，将地铁车厢中人与人之间的排斥力定义为“广义拥挤力”[1]，本文结合已有的乘客空间尺寸和广义拥挤力计算方法，通过PFC2D软件对不同车厢立席密度进行仿真研究，得到不同等级下的立席密度值k1.不同季节和携带行李条件可根据表1人体尺寸空间进行仿真模型参数修正.春秋季、常规行李携带情况下，车厢平均密度为6人/m2时，模拟结果如表2所示.

在乘客耐受感知方面，为了让乘客直观地区别其在不同乘客密度下的耐受感受，在乘客调查问卷中使用实景图像，对各交通设施出现的不同乘客密度状况进行记录，选取车厢处于不同立席密度状态时场景图8张，并进行编号.乘客在回答调查问卷时，将根据自己对地铁车厢内乘客拥挤程度的感知，按照拥挤程度“最舒适—最拥挤”共5个等级，对每张场景图进行评价[10].

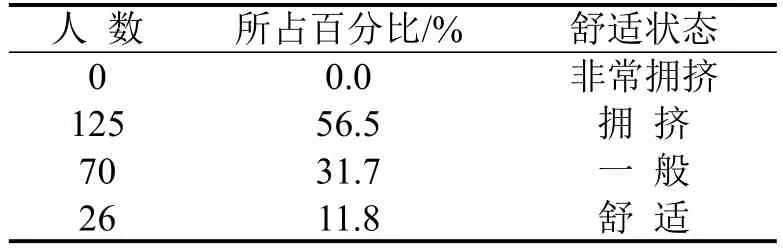
表 2 立席密度为6人/m2仿真结果Table 2 Simulation results of stand density of 6 persons/m2

根据调查结果，计算选择场景图i的立席密度为j等级的受访者所占的比例，计算公式为

式中：i代表不同乘客密度的8张场景图，i=1,…,8；j代表不同的立席密度等级，j=1,…,5，j=1为最舒适，j=5为最拥挤；Pij表示选择场景图i的立席密度等级为j的乘客数量；nij表示选择场景图i的立席密度等级为j的乘客数量；N表示接受调查的乘客总数.

立席密度等级为j的密度下界Dj为

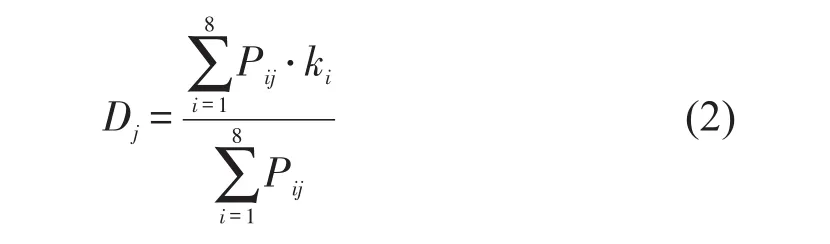
式中：ki为第i张场景图对应的立席密度.

综合不同条件下的人体空间尺寸，拥挤力仿真结果，以及乘客空间耐受感知调查结果，得到不同条件下立席密度K为

式中：k1、k2分别为仿真结果值和乘客评价值；ω1、ω2为权重.

利用顾客赋权法得到权重ω1、ω2分别为0.46和0.54.利用式(3)得到修正的立席密度等级和对应的立席密度，如表3所示.

表3 立席密度评价结果Table 3 Results of standing passenger density evaluation table

分析整理调研结果，得到不同立席密度对应的耐受感知.并规定：立席密度趋近于0时，乘客耐受感知值为0；立席密度达到《地铁设计规范》(GB50157-2003)规定的超载极限(9人/m2)时，耐受感知值为100%.进行非线性拟合得到乘客空间耐受度B与立席密度的关系，相关系数R=0.997.

式中：B为乘客空间耐受度；k为立席密度；a,b,c均为参数.

对式(4)进行空间耐受感知阈值下的立席密度k2计算，代入式(3)进行修正，结果为7.03人/m2，属于4级立席密度.一旦超过这个阈值，乘客的空间耐受性将会逼近极限，乘客出行体验急剧下降.

2.2 时间—空间综合耐受感知模型

对于乘客出行的感知评价，通常很难给出具体的数值，区间模糊数可以很好地表现乘客出行体验的感受值.根据模糊线性回归的求解思路，将乘客在线路上的耐受感知定义为模糊线性回归模型.本文将轨道交通乘客耐受性影响因素分为两个部分：第1部分为乘客的时间耐受感知，包含乘客候车时间t1和站立时间t2；第2部分为乘客的空间耐受感知，包含车厢立席密度k.这是对时间耐受感知和空间耐受感知的综合考虑结果，模型为

式中：代表时间—空间综合耐受感知值的区间模糊数；～代表回归系数的区间模糊数；、、为上述自变量的区间模糊数.这是自变量、因变量和回归系数均为区间模糊数形式，设因变量与m个自变量,…之间存在线性关系，则多元模糊线性回归模型的一般形式为

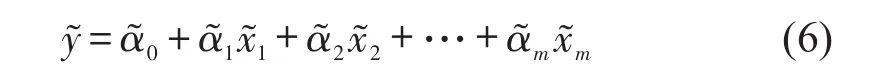
式中：是模糊常数项；是模糊回归系数.

对Q关于求一阶偏导数，得到

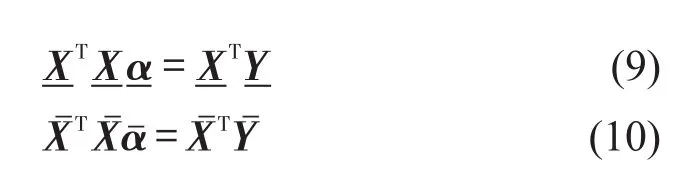
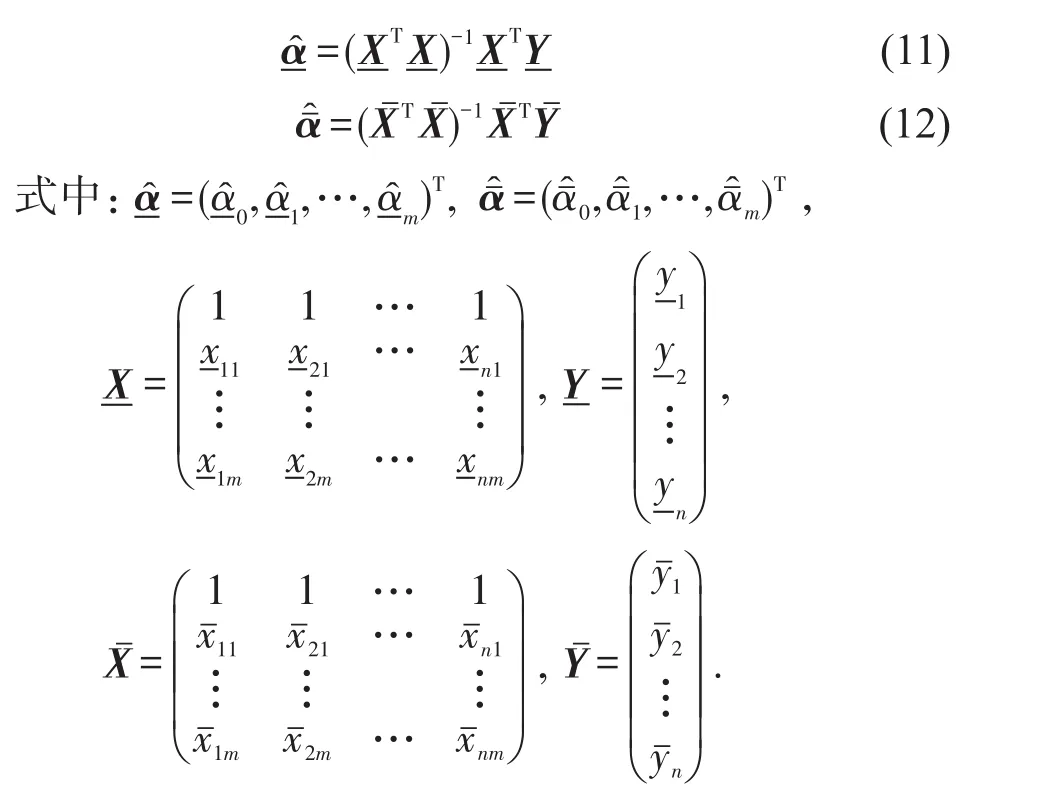
3 结果分析

3.1 耐受感知阈值分析

对重庆轨道交通出行乘客进行问卷调查，让乘客对最近一次轨道交通出行进行打分评价，为降低记忆模糊和感知误差对研究结果准确性的影响，出行者只需给出一个范围值即可.本次调查共获有效数据539份，其中，普通出行乘客253份，通勤乘客286份，取耐受值累计概率80%处为耐受阈值，耐受感知分析如图3所示，得到普通出行乘客综合耐受阈值为耐受极限的66%，通勤出行乘客综合耐受阈值为耐受极限的74%.

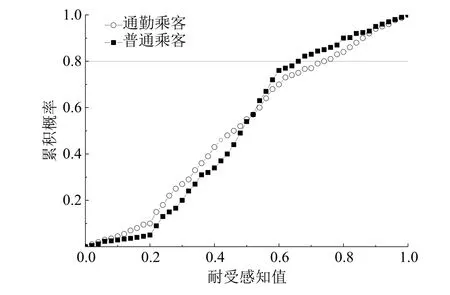
图3 耐受感知阈值分析Fig.3 Tolerance perception threshold analysis

3.2 模糊回归分析

对所收集的耐受感知数据进行标准化处理，将候车时间、站立时间、拥挤程度通过百分制比例转化为标准变量，取值范围为[0,1].这样就与相应的耐受感知变量(取值范围为[0,1])位于相同量级.对时间—空间综合耐受感知模型相应参数进行模糊回归，分别得到普通出行乘客和通勤出行乘客的耐受感知和的权重分布和回归分析，如表4所示.

从表4可以看出，对普通出行和通勤出行乘客而言，3项指标的重要程度从大到小依次为站立时间、拥挤程度、候车时间.通勤乘客比普通乘客更加重视候车时间，对站立时间和拥挤程度具有更强的耐受性，这与通勤乘客更加希望准时到达目的地而忽视车厢内部拥挤程度是相符的；通过上下界限的分析可以看出，在临近耐受感知阈值上界限的时候，拥挤程度系数明显增大，说明乘客在临近极限的时候，主要考虑车厢拥挤程度的影响，候车时间和站立时间的影响相对有限，主要是因为车厢内的拥挤情况是不停变化的，车厢处于极度拥挤的状态不会延续很长时间.将耐受感知阈值带入模糊回归方程，得到相应各变量在阈值条件下的取值变化情况，即相应要素在耐受感知等于阈值时的叠加变化情况.如图4和图5所示，实测点在空间耐受阈值的等值面上下界分布均匀，拟合情况较好.

表 4 模糊回归系数取值表Table 4 Fuzzy regression coefficient value table

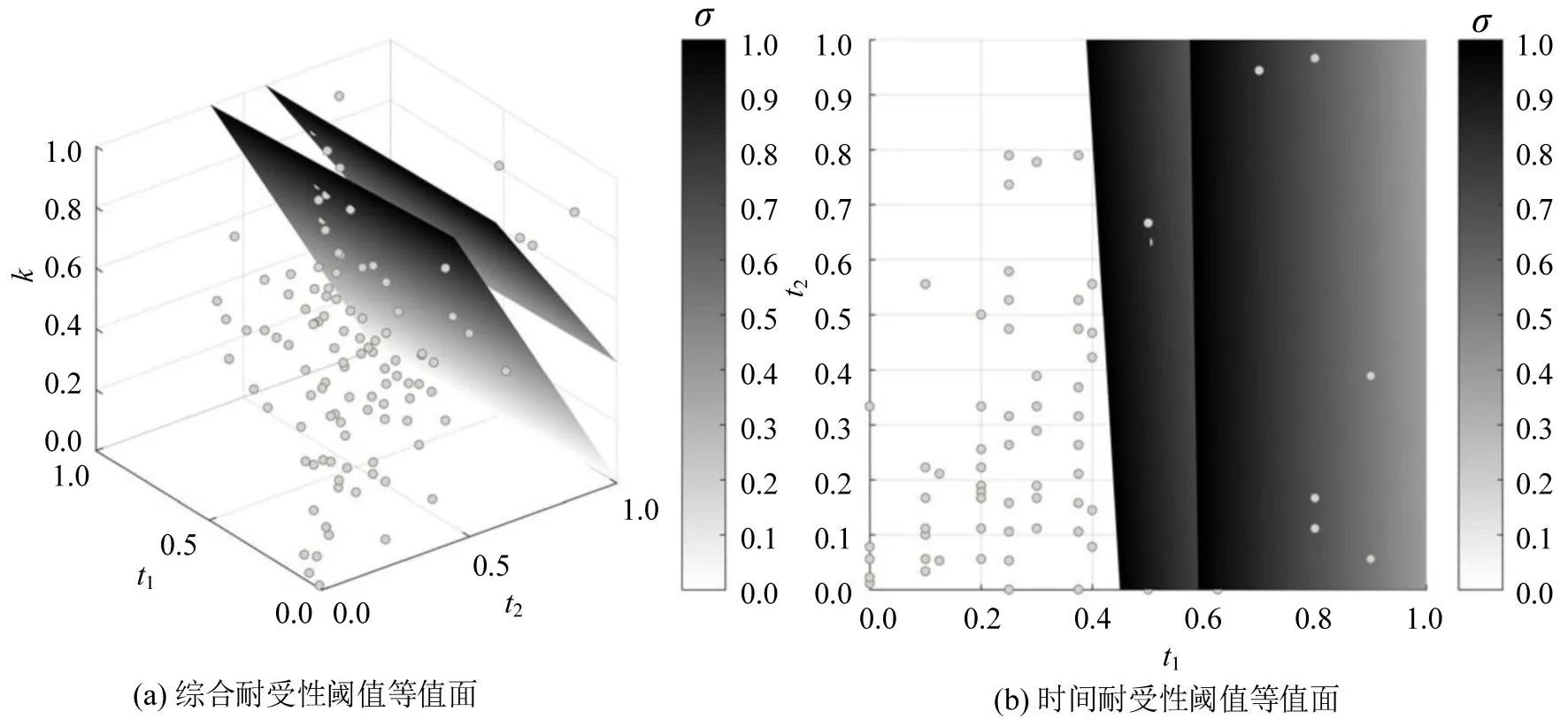
图4 普通出行乘客耐受值拟合情况Fig.4 Fit of tolerance value of ordinary passengers

图5 通勤出行乘客耐受值拟合情况Fig.5 Fit of tolerance value of commuter passengers

最后的数据分析中，将候车时间和站立时间均设置为样本空间的均值，由此得到，综合耐受阈值对应的拥挤程度变化情况，将乘客立席密度耐受感知阈值带入式(3)进行修正.得到：在普通出行环境下，人们所能接受的最大拥挤密度为6.57～6.92人/m2；在通勤出行环境下，人们所能接受的最大拥挤密度为7.21～7.63人/m2，处于空间耐受阈值7.03人/m2左右.达到阈值下界，乘客开始感到难以忍受；一旦超过阈值上界，乘客的综合耐受性将会逼近极限，乘客出行体验急剧下降.

4 结论

本文从时间—空间综合角度出发，结合乘客立席密度、站立时间、候车时间等影响因素，利用区间模糊数提出时间—空间综合耐受感知模型，结合仿真计算结果对立席密度进行修正，避免单一因素对总体目标的过度影响.通过回归分析发现，3项指标对于乘客耐受性的重要程度从大到小依次为站立时间、拥挤程度、候车时间.通勤乘客比普通乘客更加重视候车时间，对站立时间和拥挤程度具有更强的耐受性.根据研究结果对合理立席密度提出建议：在满足乘客耐受阈值条件下，普通出行环境下乘客所能接受的最大拥挤密度为6.57～6.92人/m2，通勤出行环境下乘客所能接受的最大拥挤密度为7.21～7.63人/m2.研究结果为城市规划和应急管理提供理论参考.