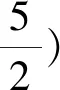应用反解系数表示法解题示例

浙江省金华市第六中学 (321000) 虞 懿

二次函数的绝对值问题一直倍受高考(竞赛)命题者的青睐，缘由是它既是我们比较熟悉的知识内容，又能考查学生综合分析问题的能力．如何有效破解此类问题呢？在各种教辅资料和试题解答中也没有一种固有的解题模式，很多时候往往采用分类讨论思想解决，但经常讨论不清楚．本文借助“反解系数表示法”去解决此类二次函数含绝对值的最值问题，旨在探索题型规律，明晰求解策略．

例1 已知函数f(x)=x2+2bx+c，设函数g(x)=|f(x)|在区间[-1,1]上的最大值为M，若M≥k对任意的b,c恒成立，试求出k的最大值．

解析：依题意可得f(0)=c,f(1)=1+2b+c,f(-1)=1-2b+c，又2=f(1)+f(-1)-2f(0)，所以2=|f(1)+f(-1)-2f(0)|≤|f(1)|+

例2 设a,b,c∈R，对任意满足|x|≤1的实数x，都有|ax2+bx+c|≤1，则|a|+|b|+|c|的最大值为．

解析：设f(x)=ax2+bx+c，由题意知|f(1)|≤1,|f(-1)|≤1,|f(0)|≤1．由f(-1)=a-b+c，f(1)=a+b+c，f(0)=c，可解得a=

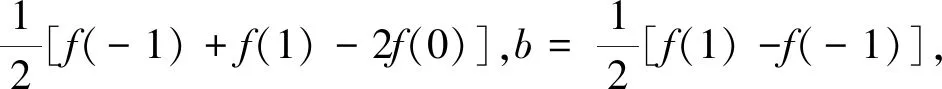
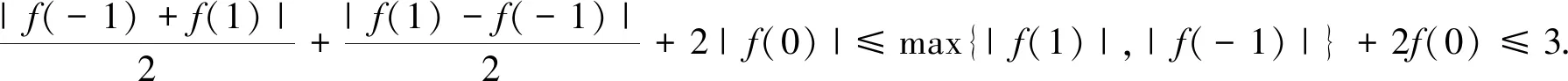
|a|+|b|+|c|=3．所以|a|+|b|+|c|的最大值为3．

例4 设F(x)=|f(x)·g(x)|,x∈[-1,1]，其中f(x)=ax2+bx+c,g(x)=cx2+bx+a，且对任意x∈[-1,1]，均有|g(x)|≤1，则F(x)的最大值为．

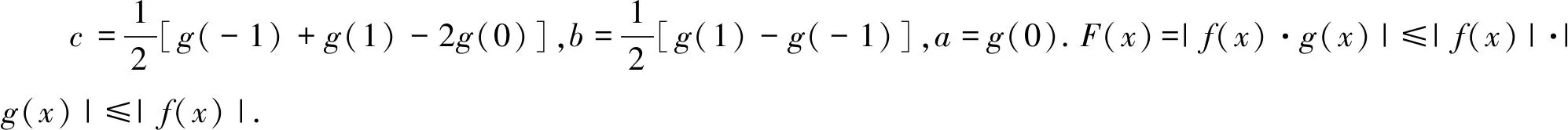
评注：将目标参系数式g(a,b,c)看作是一个函数值f(x0)，把题干中具体的参系数a,b,c看作是几个函数值f(x1),f(x2)的运算结果，再将求目标参系数式的取值范围问题视为函数在固定区域上求值域的问题，这就是我们的反解系数表示法．

巩固练习题

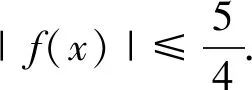
2.设函数f(x)=ax2+bx+c(a≠0)满足