高三圆锥曲线综合题的教学例析

江苏省无锡市洛社高级中学 (214187) 吴永娇 徐荣新

高三复习中圆锥曲线综合题对学生来说有一定的难度，学生面对复杂的条件和图形往往较难自主寻找到突破口，同时对于计算也存在着畏惧心理.结合圆锥曲线中重点关注椭圆的要求，笔者就高三复习中椭圆综合题的教学做一总结，与读者交流.

1.由图溯源，找突破口

对于学生来讲，圆锥曲线综合题的难点之一就是参数的选择(设点还是设直线)，为后续问题的解决开头.在很多问题中由于题目的叙述束缚了学生的思维，或者让解题思路迷茫，因此在教学中笔者常在标准方程的解决后，把图像向学生呈现，让学生观察图形思考图形的产生过程，进而确定解决问题的参数，这就是所谓的“由图溯源”.

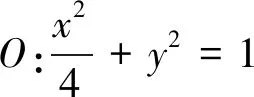
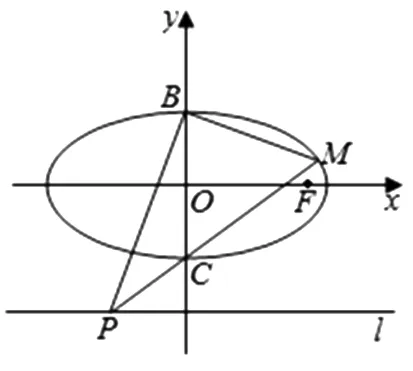
图1

(1)记直线BM，BP的斜率分别为k1，k2，求证：k1·k2为定值；

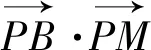
教学过程：第(1)问的教学中笔者在黑板上呈现出椭圆的方程、图形以及问题，由学生找寻图形的产生过程，进而突破难点：参数的选择.

(学生①，教师板书)图形的产生根源可以归结为直线l：y=-2上任一点P，所以设P点坐标为(m,-2)→写出直线PC方程→联立直线PC与椭圆，求出点M→可证明结论；

(学生②，教师板书)图形的产生根源可以归结为椭圆上任一点M，所以设M点坐标为(x0,y0)→写出直线MC方程→联立直线PC与直线l：y=-2，求出点P→利用点M的坐标符合椭圆方程可证明结论；

(学生③，教师板书)图形的产生根源可以归结为过C点做一条直线，分别交椭圆和直线l：y=-2于点M、P，所以设直线方程为y=kx-1→联立直线与椭圆求出M点，联立直线求出P点→可证明结论；

(学生④，教师板书)图形的产生根源可以归结为过B点做一条直线与直线l交于点P，所以直线BP方程为y=kx+1→联立直线与y=-2求出P点→写出直线PC方程→联立直线PC方程与椭圆方程，求出点M→可证明结论；

(学生⑤，教师板书)图形的产生根源可以归结为过B点做一条直线与椭圆交于点M，所以直线BM方程为y=kx+1→联立直线与椭圆求出M点→写出直线MC方程→联立直线MC方程与y=-2，求出点P→可证明结论.

在整理了几种思路后进行辨析，对可操作性和运算量进行预估，从而选择最合理的思路操作.在第(1)问解决的基础上第(2)问解答略.

现实的高三教学中，常听到同事们课后的谈论：“这节课只讲了两个题、三个题”，言语中透出淡淡的遗憾——讲的太少，但就算紧赶慢赶讲，等到批作业或者试卷时又会抱怨：“怎么还是不会啊？”的确，题干的表述有时束缚了学生的思维，而且教师也会凭着直觉、经验进行讲解，少了不同视角的剖析和比较，导致学生在做题时也视角单一、无法切入.因此教学中利用“由图溯源”的教学策略，肯花时间，让学生在辨析中突破，在比较中择优，形成思维的创造性.

2.变式教学，掌握通法

在解决圆锥曲线综合题的过程中，学生常有这样的反映：题目似曾相识，但又没有头绪，即使能操作却又不能进行到底.追根究源是通性通法的掌握不够扎实，而变式教学则能让学生在不同的情境下找寻解决问题的关键着手点以及变化之处.

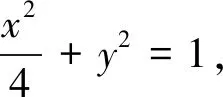
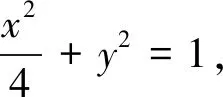
例3 已知圆C的方程为x2+y2=1，直线l1过点A(3，0)且与圆C相切.

(1)求直线l1的方程；

(2)设圆C与x轴相交于P、Q两点，M是圆C上异于P、Q的任意一点，过点A且与x轴垂直的直线为l2，直线PM交直线l2于点P′，直线QM交直线l2于点Q′，求证:以P′Q′为直径的圆总经过定点，并求出定点坐标.

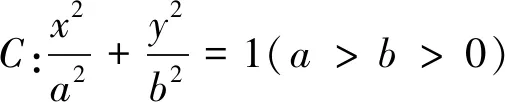
(1)求椭圆C的方程；

(2)试问：以MN为直径的圆是否经过定点？若经过，求出定点的坐标；若不经过，说明理由．

圆锥曲线的综合题中，可以基于同一个方法和相同的本质选择不同的题目，典型的做法有相同的背景下调换题目的条件和结论(如例2及变式)，或者在圆和圆锥曲线中设置相同的背景(如例3及变式).在教学中如果能经常进行变式教学，让学生感受其中的通性通法，对于提升解题能力也极有益处.勿容置疑学生能力的提升需要通过一定量题目的训练，但数量不等于质量，教师要从大量的题目中前后联系，选取富有价值的题目，反思解题思路，找寻联系与区别，在变式中强化通性通法，培养思维的深刻性.

3.加强分析，优化运算

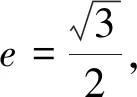
(1)求椭圆Q的方程；

①求证：OA与OB的斜率之积为定值；②求OA2+OB2；③求点N的轨迹方程；④求|NC|+|ND|的值.

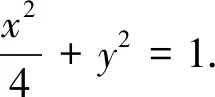
(2)设A(x1,y1),B(x2,y2),M(x0,y0)，则

因为三个点都在椭圆上，所以

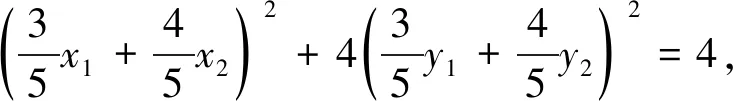
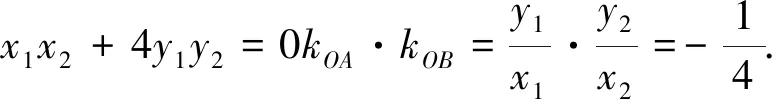
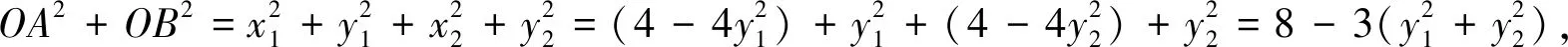
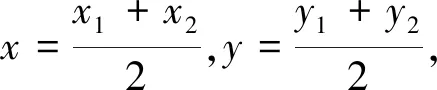
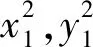
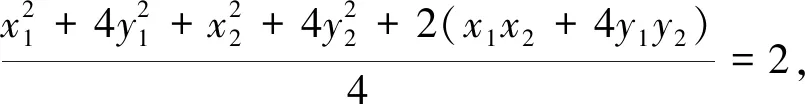
对很多同学来说，计算也是圆锥曲线综合题中一道难以逾越的鸿沟.原因主要是两个方面：一是参数选择带来运算量的难易程度(在本文的第一点已进行了梳理)；二是运算时对条件和目的分析不够导致没有方向.因此计算时要紧抓题目条件，譬如设曲线上一点，一定要注意此点所符合的表达式，为后面的消元或整体代换作铺垫，同时要关注最终的目标，这样有时会指引我们对运算式子进行适当的变形，让运算水到渠成，而不是象变戏法一样觉得不可思议.