STM分子结中电流非对称性的定性分析

钱利江,李惟驹,张义邴, 陈竞哲

(上海大学理学院,上海200444)

自从20世纪90年代扫描隧道显微镜(scanning tunneling microscopy,STM)发明之后,原子级别的器件成像技术飞速发展并趋于成熟,同时应用STM进行分子器件输运特性的研究也变得越来越普遍.一些关于分子器件的全新输运现象,比如Kondo效应[1-2]、Coulomb阻断效应[1-3]、A-B效应[3]等也渐渐被研究者们所熟悉和关注,出现了越来越多关于分子结输运电流电压(I-V)曲线的测量工作[4-5].同时分子器件的电子输运在理论研究上也是突飞猛进.Nitzan等[6]使用第一性原理对分子的电子结构进行计算,并预言单个分子可以作为新型逻辑电路的最小单位.在20世纪90年代后期,第一批应用量子输运理论的计算分子结输运性质的研究成果面世,其中非平衡格林函数作为最流行的量子输运研究方法被广泛采用[7-11].

在分子器件的研究工作中,关注点往往在于分子器件I-V曲线测量的中小偏压区域的电流响应,因为这对应着分子器件的本征电导,是集成电路的关键参数.但在I-V曲线高压区的一些反常特征却是这个尺度的一些新现象,包括非对称的I-V曲线(asymmetric I-V,AIV)[12-16]、负微分电导(negative diあerential conductance,NDC)[12-14,17-18]等.这些现象往往会出现在采用STM进行的分子器件测量中,这在某种程度上也预示着STM电极和这些现象之间有一定的关联.

在采用STM电极的分子器件实验中,分子生长在金属衬底之上,分子和衬底之间通过原子成键耦合(比如金衬底往往是通过金硫键和分子耦合);分子的另一端和STM的扫描探针相接触.这样在衬底、分子和探针之间就构成了一个电学回路,从而可以得到通过分子的电流.实验装置如图1(a)所示,获得的典型I-V曲线如图1(b)[12]所示.在这类分子器件的电学测量中,往往会得到和经典欧姆定律不同的I-V特性.例如,随着电压的增大,电流反而会减小,即NDC;或者对于一个本身结构对称的分子,其I-V曲线也会呈现出正负偏压区非对称的形状,即AIV.对于这些现象的物理来源,已有的研究对器件的描绘过于简单[15].本工作将通过有限元建模结合非平衡格林函数的方法对这一现象进行模拟和解释.

图1 STM分子结实验的实验装置示意图和典型测量数据Fig.1 Diagram of the STM molecular junction experiment setup and typical measured data

1 方法构建

针对这一纳米尺度的体系,本工作采用了有限元建模结合非平衡格林函数的方法研究其电子结构和输运性质.令一个纳米尺度器件的哈密顿量为H,左右电极的哈密顿量为HL和HR,则整个系统的哈密顿量可以写成

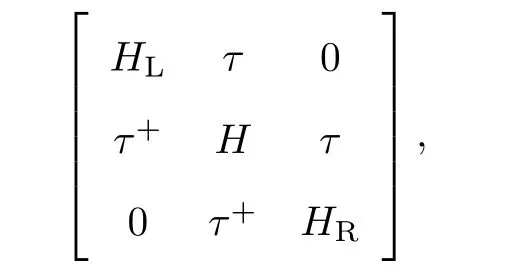
式中,τ为电极和器件的耦合.假设左右电极之间没有相互作用，所以其耦合矩阵元为0.在这样一个开放的系统中,如果计算器件的推迟格林函数,则左右电极的影响可以缩并到自能ΣL和ΣR中[7,9],即

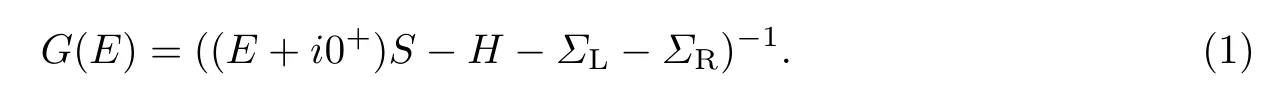
格林函数是描绘体系粒子分布的物理量.如果体系处于平衡态,则体系的电子密度可以写成

式中:A为谱函数,遵守f0为描绘电子占据情况的费米-狄拉克函数;μ为电极的化学势;

其中T为温度.

如果左右电极之间存在偏压,则体系处于非平衡态.根据Keldysh定理,体系的电子密度[10-11]可以写成

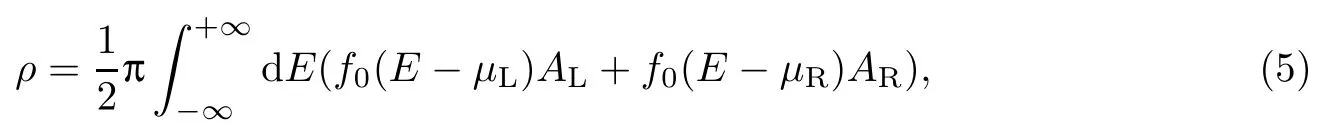
式中:AL和AR为左右电极的谱函数,即

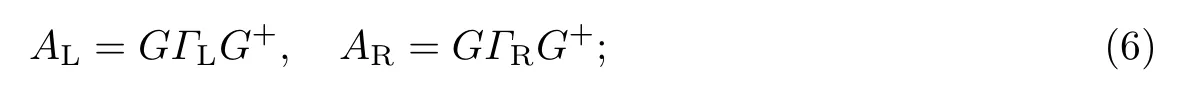
ΓL,R为电子能谱的展宽函数,即

体系的电势分布可以通过解一维泊松方程得到,即

式中,∊为器件的介电系数,ND为掺杂电荷,q为单位电荷.这样在电子密度和泊松势之间就形成了一个相互依赖的关系.

本工作通过图2所描述的一个自洽循环来得到体系被自身的哈密顿量、偏压、耦合强度等因素所影响的物理上合理的电子结构.在自洽计算收敛完成后,就可以通过格林函数来计算体系的态密度、透射几率和电流.

图2 非平衡格林函数方法的计算流程Fig.2 Calculation process of non-equilibrium Green’s function method

总态密度可以写成格林函数和交叠矩阵的乘积格式[9-11],即

占据态的态密度为

式中,非平衡格林函数G<[9-11]为

电子隧穿过体系的透射几率可以通过格林函数和耦合强度矩阵的乘积[7-10]获得，即

根据Landauder-Buttiker公式[7,10],电流可以写为

式中,费米分布函数f为

2 哈密顿量的构建

简单起见,本工作把分子器件抽象成一个一维6个等距格点的模型,格点之间的耦合关系为最近邻相互作用(见图3).

图3 六格点模型和有限元基组示意图Fig.3 Diagram of six-point model and the finite element basis

体系的哈密顿量可以写成如下的紧束缚形式:

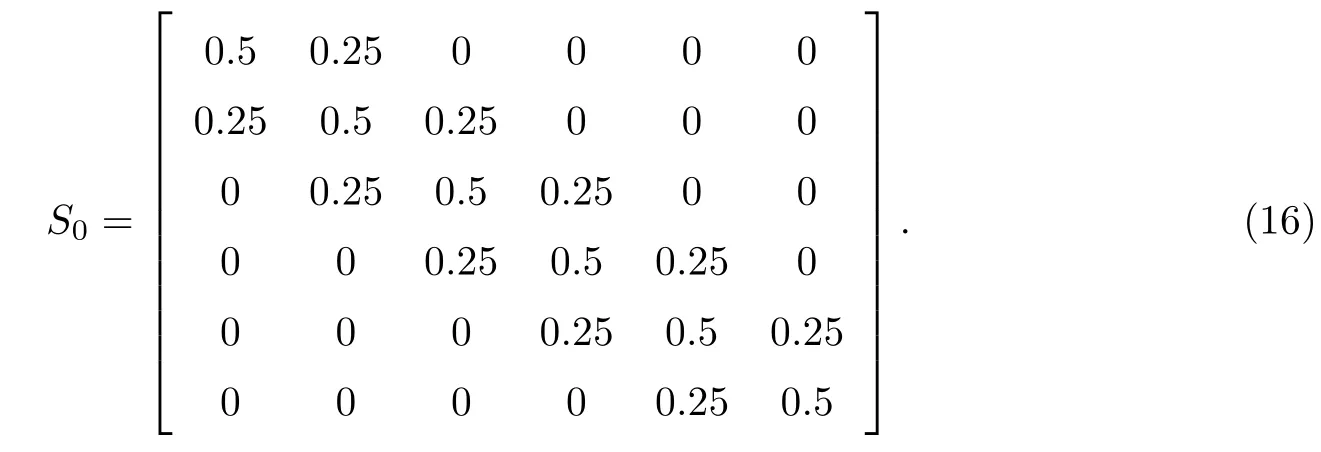
式中,H0是器件哈密顿量在实空间中的形式,其对角元的数目对应着本模型里的格点数;h0表示格点处的在位能;t0表示邻近点之间的耦合.这里的H0包括了动能和势能的贡献,三对角的形式意味着只存在近邻相互作用.这里的有限元基组为归一化的拉格朗日基函数,交叠矩阵S0按照一维有限元的格式为

3 加入局域态对器件的影响

以本工作给出的紧束缚哈密顿量为例,如果器件的第二个格点与局域态发生耦合,则系统哈密顿量可表示为

式中,h1表示局域态的在位能,t1表示局域态与器件后面格点的耦合强度.由于是局域态,t1要远小于t0.

3.1 电极的影响

半无限长的电极对器件的影响可以通过在器件哈密顿量中加入自能矩阵的方式得到.对于一维问题,模型哈密顿量在加入自能矩阵之后可表示为

式中,Σ1,Σ2分别代表左右电极所对应的自能矩阵,σ1,σ2为复数.电极的自能原则上是能量的函数,但这里采用了宽带宽近似,把电极自能处理成一个纯虚的常数,即对于所有的能级,其来源于电极的能量展宽近似为常数.这个近似对于金属的电极被证明是好用的.电极自能的模量大小代表着电极和器件耦合强度的大小.

3.2 局域态的影响

在计算模拟中,动能项决定了格点耦合强度.格点间的动能项为负,其大小取决于电子的质量设定;而势能项为在位能,其绝对值没有实际意义,但相对值反映了体系内势场的变化.动能和势能在实际体系中的大小一般为同一量级.本工作假设局域态并没有受到强烈的势场影响,在位能和电极部分相同,且自能的数值大小决定了态密度的峰宽.综上考虑,取如下参数:h0=0.6,h1=0.6,t0=-0.3,σ1=σ2=-0.2i,使得参数设置满足定性要求,相对大小合理,态密度峰清晰可见且有合适展宽.

对于局域态,令t1=0,表示完全没有耦合,同时取温度kBT=0.1.首先考察了一个没有局域态的六格点体系.这时由于系统是均匀的,所得到的I-V曲线在正偏压和负偏压区是完全对称的,在所考察的偏压区间[—1 V,1 V]内基本为一个线性函数(见图4).然后在体系中加入局域态,令局域态存在于体系的正中位置,即第3个格点和第4个格点之间,在同样的参数下,得到体系的I-V曲线如图5所示.

由图4和5可以看出,局域态的存在对于I-V曲线有一定的影响:电流的大小几乎降了一个量级;I-V曲线不再是较好的线性行为,在大约±0.6 V处出现了弯折.这里可以注意到,0.6 eV正是局域态在位能h1的值.除此之外,I-V曲线还是保持了正负偏压区的对称.

进一步地,本工作设置局域态的位置处于体系的端点,即第1个格点和第2个格点之间.这种配置对应了分子器件在STM实验中的情形.由于STM针尖的几何限制,针尖态存在一定的局域性,针尖与STM部分耦合强而与分子耦合较弱.另外,针尖的位置处于分子结的一端,引起了一定程度的结构不对称性.

在这样的配置下采用相同参数,本工作得到了体系的I-V曲线(见图6).可以发现,体系整体电流的量级与局域态处于正中的情况大致相同,但是I-V呈非对称性,电流在负偏压区较为平滑,但在较大正偏压区出现了NDC,并且电流比在负偏压区相同电压时略大,呈现出一定的极性.该结果与STM分子结实验中所观测到的结果吻合.

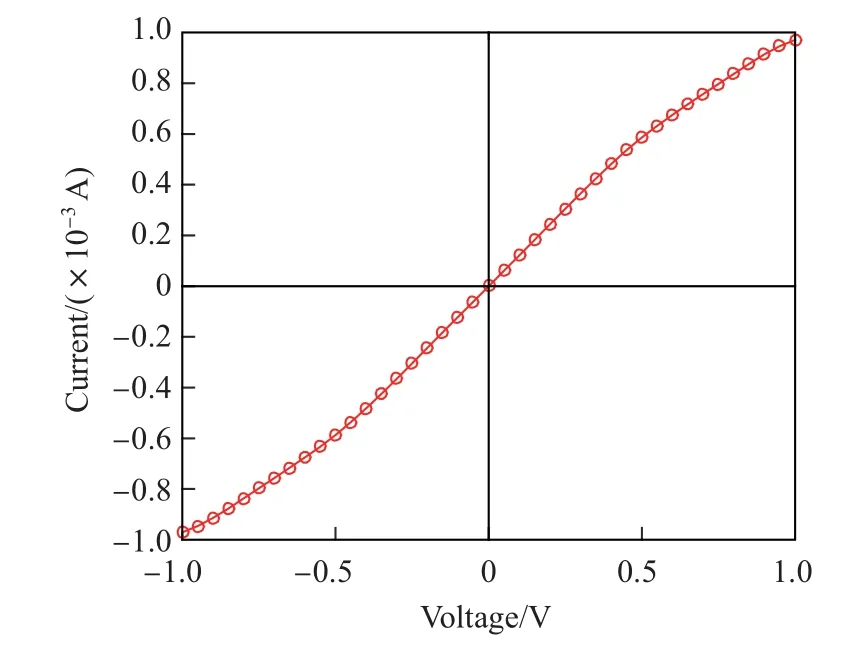
图4 无局域态的六格点模型的I-V曲线Fig.4 I-V curve of a six-point model without local states

图5 局域态在中间位置的六格点模型的I-V曲线Fig.5 I-V curve of a six-point model with local states in the center

图6 局域态在边缘的六格点模型的I-V曲线Fig.6 I-V curve of a six-point model with local states aside

为了分析导致这一现象的微观原因,本工作研究了局域态的存在对于体系态密度的影响(见图7),其中虚线为局域态处于端点的体系在平衡态(即偏压为0)下的态密度,实线为没有局域态存在的体系在平衡态下的态密度.可以看到,局域态的加入对其他态的分布也有一定影响,会使原先的态密度峰展宽或者平移.在能量约为0.6 eV附近是局域态本征的态密度,因此,原先实线的谷加上局域态的贡献之后就呈现为峰.该能量范围和局域态紧密相关.

图7 无局域态和边缘局域态的六格点模型的态密度Fig.7 Density of states of six-point models without local states or with local states aside

为了对局域态在I-V曲线中的贡献有个整体的把握,本工作分别研究了3个考察体系的态密度在偏压下的改变,结果如图8所示.可以看到,在没有局域态存在,或者有局域态且局域态处于体系正中间时,态密度对于正负偏压的变化是对称的.在这两种情况中,前者的态密度变化比较平缓,而后者比较剧烈.这是由于局域态的占据与否会引起泊松势较大的变化.而当局域态处于体系一端时,其态密度的变化呈非对称性,总态密度和占据态的态密度都随着对应电极的化学势而移动.在负偏压区,态密度的变化还仅限于峰位的线性移动.在正偏压区尤其是高电区,则引起了较为强烈的态密度峰的重整,而这正是I-V曲线中出现NDC的区域.根据这个观察结果可以得出如下结论:①由于STM所对应的针尖局域态的位置偏置,使得在正负偏压下引起了不同的非平衡态电子结构重整化,从而导致AIV曲线的出现;②NDC现象是高压下非平衡态的电子结构重整化过于剧烈导致的非线性结果.

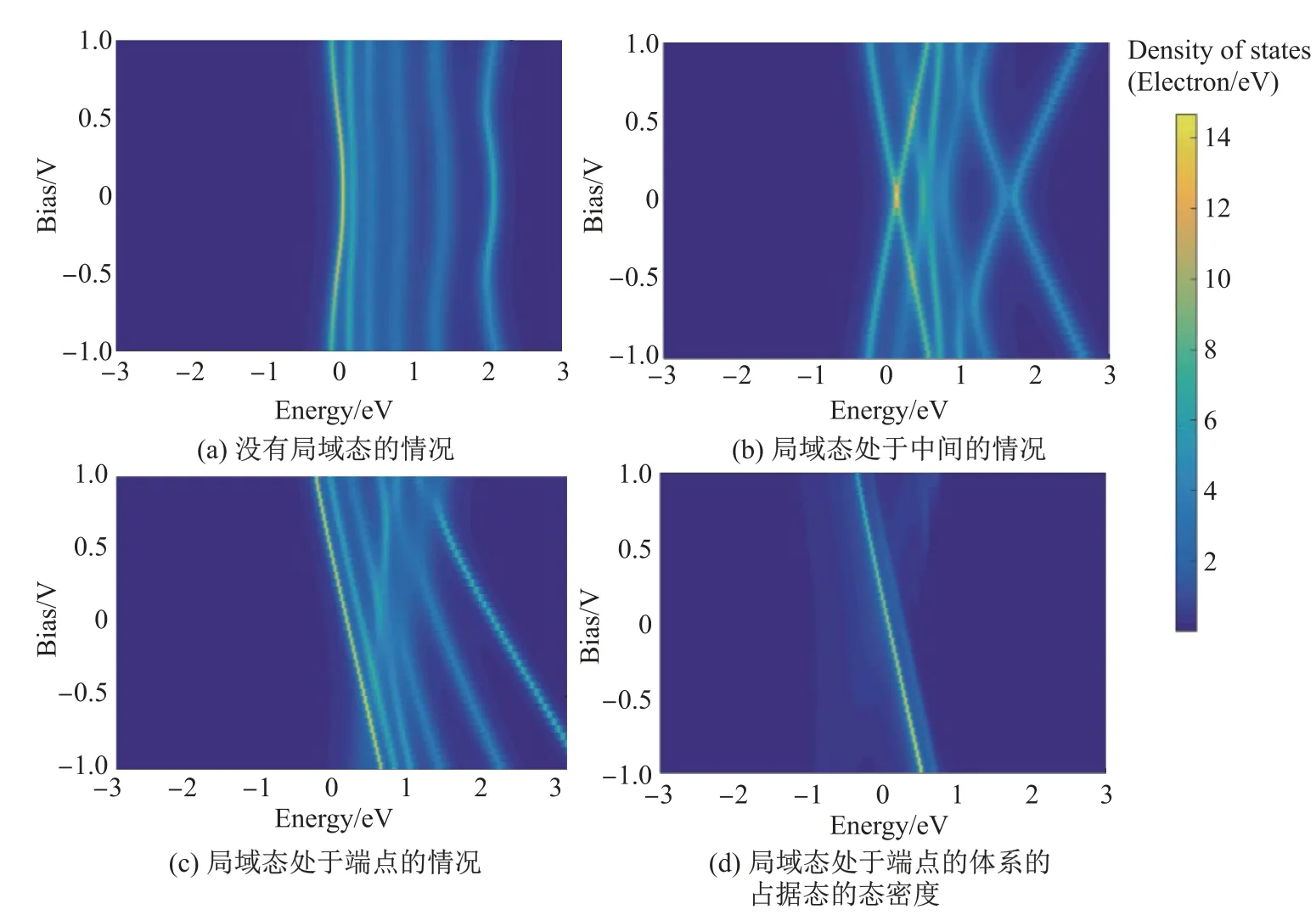
图8 各个体系中态密度随偏压和能量的变化关系Fig.8 Relations of density of states against bias and energy in all the systems

4 结束语

本工作针对STM分子器件中出现的AIV曲线和NDC现象,采用参数有限元结合非平衡格林函数的方法研究了器件的电子结构和输运性质.结果表明,STM的针尖局域态对这两个现象有重要的影响,其位置偏置状态在正负偏压下导致了非对称的电子结构重整化,这直接导致了AIV曲线的出现;而当重整化效应的强度达到一定程度时,则出现了NDC.但是由于在这类实验中,STM的位置总是处于偏置状态,所以这种现象难以避免.如果要通过外部因素进行调控,就只能通过控制局域态的局域性或者其在针尖表面态密度中的权重来进行,比如说可以选择表面比较圆滑的针尖等.