扩展颜色逻辑Petri网及其可达性分析
2020-05-13杜玉越
王 振,杜玉越,亓 亮
(山东科技大学 计算机科学与工程学院,山东 青岛 266590)
在电子商务中,一个销售者可能会同时面对多个购买者,这样的工作流程要求模型具有批处理功能和描述并发进程的能力。电子商务系统中的用户需要与其他用户进行交互,交互过程中每个用户的等待时间和系统的等待时间都是有限的。一些用户的信息可能无法及时传送给系统,这样就造成了系统中传值的不确定性,但系统不能因此而停止工作[1],这就要求模型具有描述系统中传值不确定性的功能。
Petri网是一种描述分布式系统的工具,常用来建模和分析并发、异步和分布式信息处理系统[2]。Liu等[3]提出交互Petri网(interactive Petri nets),用来描述并分析由多个子系统构成的系统。子系统之间通过信息通道来交换信息,协作完成任务。Nishi等[4]提出一种Petri网分解方法,导出了双臂集群工具的无死锁无循环时序安排(deadlock-free and non-cyclic scheduling of dual-armed cluster tools)的近似最优解,减少了计算复杂度。Ding等[5]提出适应Petri网(adaptive Petri nets)来描述自适应软件系统。它是一类混合Petri网的扩展,将神经网络算法嵌入一些特殊的变迁之中。Tiplea等[6]提出PN计算机,证明了任意递归函数都可以用Petri网计算(PN computable),同时,任意可以用Petri网计算的函数都是递归的,从而证明了PN计算机拥有图灵机的能力。Benito等[7]提出了针对时间Petri网(time Petri nets)的展开方法“时间展开法”(time unfolding),生成新的发生网,保留全部状态类别和变迁发生序列,而没有枚举全体状态空间。Liu等[8]为了得到一个小型Petri网控制器,提出可控死锁基(controllable siphon basis)的概念,证明了一个活的Petri网控制器,可以通过在每一个严格最小死锁(strict minimal siphon)上添加一个控制库所与相关弧来构成,严格最小死锁在可控死锁基之中。
但是由普通Petri网构建的系统在运行过程中可能会遇到传值的不确定性问题,导致网络系统中的变迁无法发生,系统就会陷入停止状态。因此,Du等[9]提出逻辑Petri网(logic Petri nets,LPNs)并证明LPN是等价于抑止弧Petri 网的一种增广Petri网模型,使用逻辑表达式对逻辑输入变迁的输入和逻辑输出变迁的输出进行限制,这样就可以描述系统中传值的不确定性。并且和等价的抑止弧Petri网相比,逻辑Petri网简化了网络结构,使模型的简洁度更高。Teng等[10]提出基于逻辑Petri网的模型修复方法,可以修复带有并发块的业务流程模型。逻辑Petri网中,逻辑输入表达式是一阶谓词逻辑表达式,以逻辑输入变迁的前集库所为谓词变量,表示其对应的逻辑输入变迁前集库所里面托肯的分布情况,使得前集库所中的托肯无论以任意一种组合进入逻辑输入变迁,逻辑输入表达式都能判断这个托肯组合能否让变迁使能。另一方面,逻辑输出表达式是以逻辑输出变迁的后集库所作为谓词变量的逻辑表达式,要求在逻辑输出变迁发生后,其后集库所中托肯的分布使得逻辑输出表达式为真。这样就带来逻辑输出变迁输出的不确定性,原本从A系统传来的托肯经过逻辑输出变迁之后,有可能进入B系统中,会导致信息传递的错误,系统无法正常运行。
颜色逻辑Petri网(colored logic Petri net,CLPN)[11]通过给每一个托肯染色来给不同的托肯分类。例如来自A系统的托肯和来自B系统的托肯属于不同的类别,就指定不同的颜色。这样,在逻辑输出变迁使能并且输出托肯时,需要对托肯的颜色进行判断,就能避免来自A系统的托肯进入B系统之中,从而防止信息传递错误的发生。但是,已有的CLPN内容还不完善,仅仅给出了CLPN的简单定义,它的许多分析方法甚至变迁引发规则,还是直接套用逻辑Petri网的方法。CLPN在描述多个子系统同时在网系统中运行时,需要给每个子系统都建立一个子网模型。为了减少网络冗余,提高网络运行效率,本研究提出了扩展颜色逻辑Petri网(extended colored logic Petri net,ECLPN)的概念。
1 基本定义
本节简要介绍ECLPN建立过程中用到的基本知识,包括Petri网[12]、逻辑Petri网[13]、颜色Petri网[14]以及颜色逻辑Petri网[11]。
1)Petri网PN= (P,T,F)是一个三元式,P和T是没有交集的非空有限集,其中P是库所集,T是变迁集。F是弧集,是(P×T) ∪(T×P)的子集;
2)逻辑Petri网LPN= (P,T,F,I,O,M)是一个六元式,P和T是没有交集的非空有限集,其中P是库所集,T是变迁集,T包含且仅包含三个互斥的子集:TD普通变迁集,TI逻辑输入变迁集以及TO逻辑输出变迁集。F是弧集,是(P×T) ∪(T×P)的子集。I是从逻辑输入变迁到逻辑输入表达式的映射,O是从逻辑输出变迁到逻辑输出表达式的映射。M是标识函数。
3)颜色Petri网CPN= (Σ,P,T,A,N,C,G,E,I)是一个九元式,Σ是非空颜色集合,P和T是没有交集的非空有限集,其中P是库所集,T是变迁集。A是有限的有向弧集合,N是节点函数,把A映射到(P×T) ∪(T×P)上。C是颜色函数,把P映射到Σ上。G是保护函数,把T映射到布尔型表达式上。E是表达式函数,将A映射到弧表达式上。I是初始化函数,将P映射到闭表达式上。
4)颜色逻辑Petri网CLPN=(C,P,T,F,I,O,M,IC)是一个八元式。C是由连续素数组成的有限集,每个素数表示一种托肯的颜色。P和T是没有交集的非空有限集,其中P是库所集,包含两个互补的子集:PC控制库所集和PD数据库所集。T是变迁集,T包含且仅包含三个互斥的子集:TD普通变迁集,TI逻辑输入变迁集以及TO逻辑输出变迁集。F是弧集,是(P×T) ∪(T×P)的子集。I是从逻辑输入变迁到逻辑输入表达式的映射,O是从逻辑输出变迁到逻辑输出表达式的映射。M是标识函数。IC是可容颜色指示函数,将P映射到其可以容纳的颜色集上。
2 扩展颜色逻辑Petri网
颜色逻辑Petri网[11]在描述系统中不同子系统的并发过程时,需要对每一个子系统都建立一个子网模型。对于相同结构的子系统会产生结构相同的冗余子网模型。因此,本节在颜色逻辑Petri网的基础上,给出扩展颜色逻辑Petri网的概念及与之配套的变迁使能条件与发生规则。给出多重集类型的素数表示法,并在此基础上提出了变迁使能判定定理及算法。最后提出了ECLPN可达树的构造算法。扩展颜色逻辑Petri网能有效继承逻辑Petri网和颜色Petri网对现实系统描述与分析的优点,保证系统在运行过程中的正确性。
2.1 扩展颜色逻辑Petri网定义
定义1(扩展颜色逻辑Petri网)ECLPN={Σ,P,T,A,N,C,G,E,Init,I,O,M}称为扩展颜色逻辑Petri网,当且仅当
1) Σ是非空托肯颜色的集合。
2)P是有限库所的集合。
3)T=TI∪TO∪TD∪TL是有限变迁的集合。其中
(a)TI是逻辑输入变迁集合,用来描述向变迁传入数据时的不确定性。对∀t∈TI,变迁t的引发受到t的输入库所集逻辑表达式fI(t)的限制,fI(t)中的谓词变量包含t所有输入库所中可能出现的颜色,称fI(t)为逻辑输入表达式。
(b)TO是逻辑输出变迁集合,用来描述从变迁传出数据时的不确定性。对∀t∈TO,变迁t引发后的结果受到t输出库所集上的逻辑表达式fO(t)的限制,fO(t)中的谓词变量包含t所有输出库所中可能出现的颜色,称fO(t)为逻辑输出表达式。
(c)TL是逻辑变迁集合,用来描述向变迁传入数据和从变迁传出数据时的不确定性。对∀t∈TL,变迁t的引发受到t的输入库所集逻辑表达式fI(t)的限制,引发后的结果受到t输出库所集上的逻辑表达式fO(t)的限制,fI(t)与fO(t)的定义与(a)和(b)之中相同,同时分别被称为逻辑输入表达式和逻辑输出表达式。
(d)TD是普通变迁集合,引发与输出均不受逻辑表达式的限制。
4)A是有限的有向弧集合,且P∩T=P∩A=T∩A=Ø。对于p∈P,t∈T,(p,t)被称为p的输出弧或者t的输入弧。(t,p)被称为t的输出弧或者p的输入弧。
5)N:A→ (P×T)∪(T×P)是一个节点函数。
6)C:P→ Σ 是颜色函数,功能是将托肯指定一个颜色。
7)G映射T到布尔型表达式,是一个保护函数,使得
∀t∈T:Type(G(t)) =B∧Type(Var(G(t)))⊆Σ;
保护函数G映射每一个变迁t∈T到一个布尔型表达式,并且G(t)中每一个变量的类型值必须在Σ中。当省略保护表达式时,表示其值为真值true。
8)E映射A到弧表达式的集合,集合由可以接受的弧表达式构成,弧表达式用多重集来表示,用来描述这条弧的权重。
(a) 对于(p,t) ∈A,若t∈TI∪TL,则t所有输入弧表达式中出现的托肯类型可以使fI(t)为真;
(b) 对于(t,p)∈A,若t∈TO∪TL,则t所有输出弧表达式中出现的托肯类型可以使fO(t)为真。
9)Init映射P到闭表达式,是一个初始化函数,使得
∀p∈P:Type(Init(p)) =C(p)MS。
10)I是一个逻辑限制输入函数,使对∀t∈TI,I(t) =fI(t)。
11)O是一个逻辑限制输出函数,使对∀t∈TO,O(t) =fO(t)。
12)M:P→ ΣMS是一个标识函数,∀p∈P,M(p)表示p中的有色托肯多重集,描述库所p中托肯的种类和数量。在某一时刻由全体M(p)组成的集合{M(p) |p∈P}称为标识,记作M,描述网络在这一时刻的状态。
下面对E(p,t)〈b〉做进一步说明。
假设t∈T,p∈·t,绑定b,弧(p,t)上的弧表达式集合E(p,t)〈b〉。对于弧(p,t),若t∈TD∪TO,则t的使能条件只有一种情况,从而弧(p,t)上可以接受的表达式只有一个,此时E(p,t)〈b〉是一个单元素集合。同理,对于弧(t,p),t∈TD∪TI,p∈t·,E(t,p)〈b〉也是一个单元素集合。如果t∈TI∪TL,p∈·t,由于逻辑输入变迁所表示的传值不确定性,则E(p,t)〈b〉内可以接受的表达式不少于一个。例如,对于绑定b= 〈v1=s,v2=b1,v3=b2〉。如果t∈TI∪TL,需要满足逻辑表达式·T·∨b1∨b2,那么E(p,t)〈b〉可以接受的表达式集合为E(p,t)〈b〉={Ø,b1,b2,b1+b2}。同理,如果t∈TO∪TL,p∈t·,那么E(t,p)〈b〉内元素个数不少于一个。
可以证明ECLPN与CLPN的等价性。根据参考文献[9],判断两类Petri网是否等价的条件是它们的可达标识图是否同构(isomorphism)。对于CLPN的任意一个变迁t,定义一个映射f,将该变迁的所有前集库所和后集库所分别合并成一个库所,库所内托肯根据其源库所染色,通过弧上表达式来控制该变迁的发生,即可得t在ECLPN中等价的变迁。可以证明f是一个双射,即可得ECLPN和CLPN的可达标识图是同构的,即ECLPN与CLPN等价,对业务流程的表达能力是相同的。
为了方便引出变迁的使能条件和引发规则,下面定义多重集的计算。
定义2假设多重集MS,MS中有n个元素,这些元素表示类型,构成“类型元素”集合Elem= {e1,e2,…,en},则每种类型元素的系数构成系数集合,定义为H(Elem) = {h(e) |e∈Elem},其中h(e)是e在多重集MS中的系数,表示类型元素e在MS中的数量。多重集内所有类型元素的数量定义为|MS| = ∑e∈Elemh(e)。函数S:MS→Elem表示从多重集映射到多重集所包含类型元素的集合。
例如,对于多重集MS= 3a+4b+c,类型元素集合Elem= {a,b,c},H(Elem) ={3, 4, 1},|MS| = 3 + 4 + 1 = 8,S(3a+4b+c) = {a,b,c}。
下面讨论ECLPN中变迁的使能条件和引发规则,ECLPN中变迁的使能条件包含变迁前集中托肯分布和托肯颜色两个条件。
定义3(扩展颜色逻辑Petri网中变迁的使能条件和引发规则)假设ECLPN={Σ,P,T,A,N,C,G,E,Init,I,O,M},M是它的一个标识,对于一个绑定b,
1)变迁t∈T的使能条件为:
(a)对于∀t∈TO∪TD,称t在M下是使能的,当且仅当
∀p∈·t:E(p,t)〈b〉≤M(p)
(b)对于∀t∈TI∪TL,称t在M下是使能的,当且仅当
①∀p∈·t,∃MSI∈E(p,t)〈b〉,使得MSI≤M(p);
②∪p∈·tS(MSI)使fI(t)为真。
若变迁t在M是使能的,则可以引发,记作M[t>,且引发后产生一个后继标识M′,记作M[t>M′。
2)变迁t∈T的引发规则为:
(a)对于t∈TD,
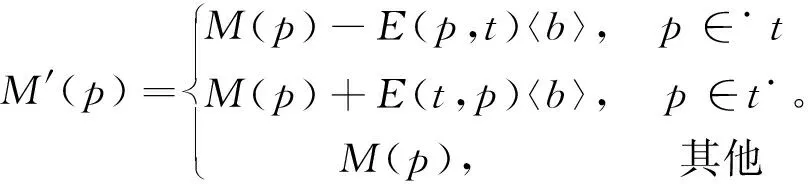
(b)对于t∈TI,
其中,{MSI}为满足使能条件中①和②多重集的集合,是E(p,t)〈b〉的子集。
(c)对于t∈TO,t发生后相关库所内有色托肯改变时要满足以下条件
①∀pa∈t·,∃MSout∈E(t,pa) 〈b〉,∃pb∈·t,使得MSout≤M(pb)。
②∪pa∈t·S(MSout)使fO(t)为真;
其中,{MSout}为满足条件①和②多重集的集合,是E(t,p)〈b〉的子集。
(d)对于t∈TL,t发生后相关库所内有色托肯改变时要满足以下条件
①∪pa∈t·S(E(t,pa)〈b〉)使fO(t)为真;
②∀pa∈t·,∃MSout∈E(t,pa) 〈b〉,∃pb∈·t,使得MSout≤M(pb)
2.2 多重集元素类型的素数表示法
为了简化实际应用中判断变迁使能的过程与可达标识的计算,下面引入多重集类型元素到素数的映射与多重集到素数幂乘积的映射,用一个整数(素数幂的乘积)集合来表示可达标识,和有向弧上的表达式。

例如,对于一个多重集MS= 3a+4b+c,其类型元素集合Elem= {a,b,c}对应前3个素数{2, 3, 5},则多重集MS唯一确定的整数为fint(MS) = 23×34×51= 3 240。反之,整数3 240唯一确定一个多重集fMS(3 240) =fMS(23×34×51) = 3a+4b+c。对于多重集集合{MS} = {a+b,b+c},fint(MS) = {6, 15},反之,fMS({6, 15}) =fMS({2×3,3×5})={a+b,b+c}。
素数幂表示法的局限性,在于素数幂的乘积不能大过这个数据类型所能支持的最大整数。例如,如果用一个32位的无符号长整型来存储这个乘积,那么这个乘积不能超过232- 1 = 4 294 967 295。能容纳单种类素数的上限为31个2,20个3,13个5或者11个7等等,即对于单类型来说,类型为2的托肯不能超过31个,类型为3的托肯不能超过20个,类型为5的托肯不能超过13个,类型为7的托肯不能超过11个,此时占用内存空间为32位。
实际上对于有n个元素类型的多重集来说,可以使用(n-1)个素数幂组成的数组来存储。此时占用内存空间为(n-1)×32位。例如,对于有4个类型的多重集,3个素数幂组成的数组能容纳单种类素数的上限为93个2,60个3,39个5或者33个7。多重集93a+0b+0c+0d可以使用数组(231, 231, 231)来存储;多重集0a+60b+0c+0d,可以使用数组(320, 320, 320)来存储,此时这种“混合表示法”占用的内存空间为3×32位。
如果系统运行过程中托肯数量和类型数量超过素数幂的表示范围,那么就用n位整数构成的数组来储存多重集,每个整数代表了某一类托肯元素的数量,其数量最多可以达到232-1,占用的内存空间为n×32位。
下面基于素数表示法给出变迁使能的判定定理。
定理1设ECLPN={Σ,P,T,A,N,C,G,E,Init,I,O,M},M∈R(M0),R(M0)表示M0的可达标识。对于绑定[14]b∈B,
1)∀t∈TO∪TD,M[t>当且仅当∀p∈·t,fint(M(p))可以整除fint(E(p,t))〈b〉,记作fint(M(p)) |fint(E(p,t)〈b〉)。
2)∀t∈TI∪TL,p∈·t,M[t>当且仅当∃fint(MSI)∈fint(E(p,t)〈b〉),使得fint(M(p))|fint(MSI) 且∪p∈·tS(MSI)使fI(t)为真。
证明:[必要性]
1)当t∈TO∪TD时,如果M[t>,由定义3的1)得
∀p∈·t:E(p,t) 〈b〉≤M(p)。
假设多重集E(p,t)〈b〉与多重集M(p)的类型元素集合均为Elem= (e1,e2, …,en),E与素数集Dn=(d1,d2, …,dn)在元素上一一对应。E(p,t)〈b〉类型元素集合的系数集合为HE(Elem) = (hE1,hE2, …,hEn),M(p)类型元素集合的系数集合为HM(E) = (hM1,hM2, …,hMn)。
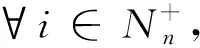
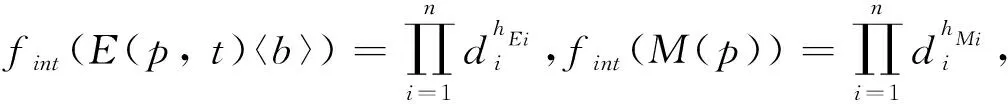
2)当t∈TI∪TL,如果M[t>,由定义3的2)有∀p∈·t,∃MSI∈E(p,t)〈b〉,使得MSI≤M(p),类似于(1)的证明过程,将E(p,t)〈b〉替换为MSI,可得∃fint(MSI)∈fint(E(p,t)〈b〉),使得fint(M(p))|fint(MSI),同时由M[t>可得∪p∈·tS(MSI)使fI(t)为真。
[充分性]

2)对于t∈TI∪TL,由∃fint(MSI)∈fint(E(p,t)〈b〉),使得fint(M(p))|fint(MSI),且在∪p∈·tS(MSI)使fI(t)为真的前提下,类似于(1)的证明过程,将E(p,t)〈b〉替换为MSI,可得MSI≤M(p),因此M[t>。[证毕]
根据定理1,下面给出变迁的使能判定算法。
算法1变迁使能判定算法
输入:ECLPN={Σ,P,T,A,N,C,G,E,Init,I,O,M},M∈R(M0),t∈T;
输出:t是否使能
Step0:若t∈TD∪TO,则进入Step1,否则进入Step2;
Step1:对∀p∈·t,判定是否有fint(M(p)) |fint(E(p,t)〈b〉)成立,若成立,则输出t使能,否则输出t不使能;
Step2:对∀p∈·t,判断在E(p,t)〈b〉中是否存在一个表达式MSI对应的整数fint(MSI),使得fint(M(p)) |fint(MSI)成立,若存在,则进入Step3,否则输出t不使能;
Step3:对∀p∈·t,判断∪p∈·tS(MSI)能否让fI(t) |M为真,若为真则输出t使能,否则输出t不使能。
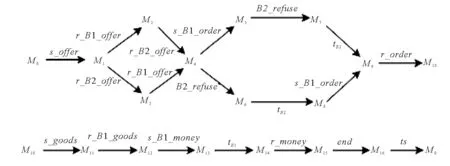
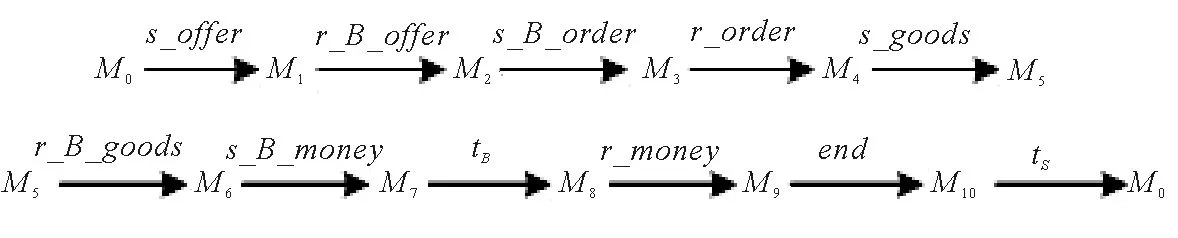
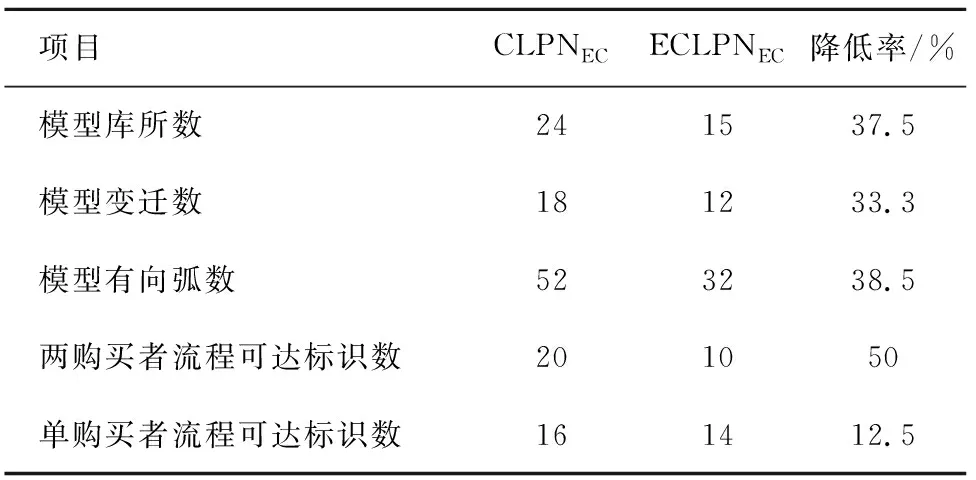
对于一个给定变迁,算法1给出了判定其使能的方法。如果t∈TD∪TO,只需要判断∀p∈·t,fint(M(p)) |fint(E(p,t)〈b〉)是否成立即可。因此,其时间复杂度为O(m),m是t前集中库所的数量。如果t∈TI∪TL,则需要判断在∀p∈·t,E(p,t)〈b〉中是否存在一个表达式MSI对应的整数fint(MSI),使得fint(M(p)) |fint(MSI)成立,判断逻辑表达式fI(t) |M能否成立只需代入即可判断,故其时间复杂度为O(m×n),n为E(p,t)〈b〉中表达式的数量。另一方面,在[11]中定理1给出的向量匹配方法也可以判定变迁是否使能,如果t∈TD,则需要将t的使能向量Vi与标识M按位比较,因此其时间复杂度为O(r),r为CLPN中全体库所的数目。如果t∈TI∪TO,则需要首先在逻辑输入/输出向量组中找到一个符合逻辑条件的向量,然后再与标识M按位比较。假设逻辑输入/输出向量组中有s个向量,判断是否符合逻辑条件需要进行r位向量的按位比较,找出符合条件的向量V之后,需要将V与M按位比较,则这个过程的时间复杂度为O(s×r2)。虽然对于t∈TD,有O(m) =O(r),但是,对于t∈TI,有O(m×n) 虽然由于系统中数据的不确定性,逻辑输入变迁与逻辑变迁使能的标识不止一种,同时逻辑输出变迁或者逻辑变迁发生后产生的标识也不止一种,但是在实际工作流程中,每个库所中有色托肯的分布是确定的,对应一个确定的整数。因此,为了方便可达标识的表示与计算,下面定义输出矩阵与输入矩阵。 根据输入矩阵与输出矩阵,给出ECLPN关联矩阵的定义。 定义6假设ECLPN= {Σ,P,T,A,N,C,G,E,Init,I,O,M},则ECLPN的颜色逻辑关联矩阵(colored logic incidence matrix)可以表示如下: AM=[aij]n×m, 如果ECLPN中的一个变迁发生,那么一步可达标识的计算公式可以由下面结论给出。 定理2设ECLPN={Σ,P,T,A,N,C,G,E,Init,I,O,M},M∈R(M0),AM是颜色逻辑关联矩阵,AMi*表示AM的第i行向量。对于t∈T,若M[t>M′,则标志从中元素按AM中列标签(库所)顺序排列之后得到向量VM,M′对应的向量为VM′, fint(VM′) =fint(VM) ⊗AMi*。 (1) 其中fint(VM) ⊗AMi*表示fint(VM)与AMi*进行按位乘法运算。 证明: 下面提出ECLPN的可达树构造算法。 算法2:ECLPN可达树构造算法 输入:ECLPN= {Σ,P,T,A,N,C,G,E,Init,I,O,M}; 输出:ECLPN的可达树RT Step0:初始化 Step0.1:将初始标识M0用Init函数初始化,得到库所集P0= {p0|M0(p0)≠Ø}; Step0.2:根据实际运行情况来初始化ECLPN中每条有向弧上面的表达式; Step0.3:用颜色集Σ指定托肯的类型,构造绑定b。 Step1:将初始标识M0对应的整数fint(M0)作为RT的根节点,并标记为“新”; Step2:若存在一个“新”节点,将其标记为M,并执行以下操作 Step2.1:在此标识下,对每个t∈T,根据算法1判断是否使能,可得到在当前标识下所有使能的变迁,根据定理2的一步可达标识的计算公式可以得到新可达标识对应的整数,将这个整数形成节点,并将这些节点标记为“新”;从M到所有“新”节点用一条有向弧连接,箭头指向“新”节点,并且在弧上标记引发的变迁,删除M上的“新”; Step2.2:如果从M0到M的有向路上存在一个节点Node,使得Node=M,那么在节点M上标注为“旧”,并返回到Step2; Step2.3:如果∀t∈T:M[t>,则在节点M上标注为“端点”,并返回Step2。 算法2的主要计算过程集中在Step2.1判断变迁使能与计算新可达标识上。 1)对于判断变迁使能的过程,前面的讨论已经得出算法1在时间复杂度上比[11]的定理1低。 2)对于计算新可达标识的过程,在算法2中,根据公式(1),对于∀t∈T,因为需要进行按位乘法,所以其时间复杂度为O(u×rE),rE为ECLPN中全体库所的数目,u是当前标识下使能变迁的数量。另一方面,在[11]中的算法1,对于∀t∈T,因为需要进行向量的按位加法,所以其时间复杂度为O(u×r),r为CLPN中全体库所的数目。 由O(u×rE) =O(u×r)以及(1),可得算法2比[11]中可达树构造算法(算法1)时间复杂度低。 在本节首先给出一个电子商务的实例,然后分别用CLPN[11]和ECPLN建立模型CLPNEC和ECLPNEC,并进行对比分析。 对于一个电子商务系统,在一次交易过程中,通常不仅仅存在一个买方和一个卖方,本节以一个卖方和两个买方进行的交易过程为例。这个过程要求模型具有批处理功能和应对数据传值不确定性的方法。利用[13]中图3.3的LPN模型来描述一次交易的流程,用Seller代表卖家,分别用B1和B2表示买家1和买家2。开始时,Seller向B1和B2发送广告(s_offer)告知Seller处有商品。B1收到广告(r_B1_offer)后,如果购买,则会向Seller下订单(s_B1_order)。Seller收到订单(r_order)之后开始准备货物。B2收到广告(r_B2_offer)后,如果不购买,那么执行拒绝操作(B2_refuse)。B2在本次流程中任务完成,初始化(tB2)后等待开始新的流程。Seller的货物准备完毕之后向B1发送货物(s_goods),B1收到货物(r_B1_goods)之后向Seller付钱(s_B1_money)。B1在本次流程中任务完成,初始化(tB1)后等待开始新的流程。Seller在收到钱(r_money)后在本次流程中任务完成,结束系统流程(end)后进行初始化(tS),等待开始新流程。 在[13]中图3.3的模型LPN=(P,T,F,I,O,M)基础上定义托肯颜色集C,可容颜色集[11]IC(P),即可得电子商务实例的CLPNEC模型。其中,C= {2, 3, 5},IC(P) = {IC(iS) = {2},IC(iB1) = {3},IC(iB2) = {5},IC(B1_offer) = {2},IC(B2_offer) = {2},IC(p11) = {3},IC(p1) = {2},IC(p21) = {5},IC(B1_order) = {3},IC(B2_order) = {5},IC(p12) = {3},IC(p2) = {2},IC(p22) = {5},IC(B1_goods) = {3},IC(B2_goods) = {5},IC(p13) ={3},IC(p3) = {2},IC(p23) = {5},IC(B1_money) = {3},IC(B2_money) = {5},IC(OB1) = {3},IC(OB2) = {5},IC(p4) = {2},IC(OS) = {2}},包含库所24个,变迁18个,有向弧52条。 下面构建模型CLPNEC的可达树。用向量表示CLPNEC的可达标识。向量中每一位数值对应库所为:{iS,iB1,iB2,B1_offer,B2_offer,p11,p1,p21,B1_order,B2_order,p12,p2,p22,B1_goods,B2_goods,p13,p3,p23,B1_money,B2_money,OB1,OB2,p4,OS}。假设在这个电子商务实例中,其初始标识为M0= {111000000000000000000000}。根据[11]的算法1构建出的可达树分别如图1、2所示。 图1为两购买者流程CLPNEC的可达树,B1和B2均从Seller购买货物。为了降低可达树的规模,在构建CLPNEC可达树图1的过程中应用规则:可以并发的变迁前后相邻发生,也就是这两个变迁之间不能有其他变迁发生。 图1 两购买者流程的CLPNEC可达树Fig. 1 CLPNEC RT for two purchasers process 其中,每个可达标识的托肯分布如下: M0= {111000000000000000000000},M1= {011110100000000000000000}, M2= {001011100000000000000000},M3= {010100110000000000000000}, M4= {000001110000000000000000},M5= {000000111010000000000000}, M6= {000001100100100000000000},M7= {000000101110100000000000}, M8= {000000000011100000000000},M9= {000000000010111010000000}, M10= {000000000000101110000000},M11= {000000000010010011000000}, M12= {000000000000000111000000},M13= {000000000000000011101000}, M14= {000000000000000110010100},M15= {000000000000000010111100}, M16= {010000000000000010110100},M17= {001000000000000010111000}, M18= {011000000000000010110000},M19= {011000000000000000000010}, M20= {011000000000000000000001}。 图1中可达标识的数量为20。 图2为单购买者流程CLPNEC的可达树,B1从Seller购买货物,B2不购买货物。为了降低可达树规模,在构建CLPNEC可达树图2的过程中应用下面的规则: 图2 单购买者流程的CLPNEC可达树Fig. 2 CLPNEC RT for one purchaser process 图3 电子商务实例的ECLPNEC模型Fig. 3 ECLPNEC for an E-commerce instance 1)tB1,tB2,tS,使能时优先发生。 2)r_B1_offer与r_B2_offer之间不能有其它变迁发生。 3)s_B1_order与B2_refuse之间不能发生其它变迁。 4) 1)的优先级高于2)、3)的优先级。 同理,可以写出每个可达标识的托肯分布,此处省略。图2中可达标识的数量为16。 由于无购买者与两个购买者的购买流程是等价的,故省略无购买者购买过程。 CLPN在其定义中限制了库所的容量为1,导致其库所中不能存在两个及两个以上的托肯。因此,如果要描述多个子系统的并发过程,须为每个子系统都建立一个子网。而ECLPN将相同结构的多个子系统用一个子网表示,且在这个子网中,用不同颜色的托肯表示不同子系统并发过程。 电子商务实例的ECLPN模型ECLPNEC如图3所示,其中变迁B_refuse,s_B_order,r_order,s_goods,r_B_goods,s_B_money与tB是逻辑变迁,r_money是逻辑输入变迁,逻辑表达式在下文给出。在ECLPNEC中,颜色集∑= {s,b1,b2},s代表Seller,b1代表B1,b2代表B2。∑对应的素数集为D3= {2, 3, 5},绑定b= {v1=s,v2=b1,v3=b2},在网络运行过程中不发生改变。 与CLPNEC相比,ECLPNEC将具有相同结构的买家子系统B1和B2用一个子系统Buyer来代替,卖家子系统Seller不变。在子系统Buyer中,通过使用不同的颜色来表示托肯的来源,不同颜色托肯的运行过程表示不同子系统的运行流程。变迁输入弧上的表达式表示变迁发生时需要的托肯数量和颜色,变迁输出弧上的表达式表示变迁发生后向其后集输入的托肯数量与颜色。有向弧上表达式根据系统的具体情况进行设置。ECLPNEC中包含库所15个,变迁12个,有向弧32条。 下面根据算法1构建ECLPNEC的可达树,用向量表示ECLPNEC的可达标识,向量中的每一位对应的库所为{iS,iB,B_offer,p11,p1,B_order,p12,p2,B_goods,p13,p3,B_money,OB,p4,OS},其初始标记M0= {s,b1+b2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},整数化之后得到fint(M0) = {2, 15, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}。 在ECLPNEC中, 1)B_refuse是逻辑变迁,其逻辑输入输出表达式均为fI=fO=·T·∨b1∨b2。 2)s_B_order是逻辑变迁,其逻辑输入输出表达式均为fI=fO=·T·∨b1∨b2。 3)r_order是逻辑变迁,其逻辑输入输出表达式均为fI=fO=s∧(·T·∨b1∨b2)。 4)s_goods是逻辑变迁,其逻辑输入输出表达式均为fI=fO=s∧(·T·∨b1∨b2)。 5)r_B_goods是逻辑变迁,其逻辑输入输出表达式均为fI=fO=·T·∨b1∨b2。 6)s_B_money是逻辑变迁,其逻辑输入输出表达式均为fI=fO=·T·∨b1∨b2。 7)tB是逻辑变迁,其逻辑输入输出表达式均为fI=fO=b1∨b2。 8)r_money是逻辑输入变迁,其逻辑输入表达式为fI=s∧(·T·∨b1∨b2)。 9) 其余变迁均为普通变迁。 ECLPNEC有向弧上的表达式如下所示: 1)变迁的输入弧 (a)E(iS,s_offer)〈b〉= (s),fint(E(iS,s_offer)〈b〉) = 2; (b)E(iB,r_B_offer)〈b〉 = (b1+b2),fint(E(iB,r_B_offer)〈b〉) = 15; (c)E(B_offer,r_B_offer)〈b〉 = (s),fint(E(iB,r_B_offer)〈b〉) = 2; (d)E(p1,r_order)〈b〉 = (s),fint(E(p1,r_order)〈b〉) = 2; (e)E(p11,s_B_order)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(p11,s_B_order)〈b〉) = (1, 3, 5, 15); (f)E(p11,B_refuse)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(p11,B_refuse)〈b〉) = (1, 3, 5, 15); (g)E(B_order,r_order)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(B_order,r_order)〈b〉) = (1, 3, 5, 15); (h)E(p2,s_goods)〈b〉 = (s,s+b1,s+b2,s+b1+b2),fint(E(p2,s_goods)〈b〉) = (2, 6, 10, 30); (i)E(p12,r_B_goods)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(p12,r_B_goods)〈b〉) = (1, 3, 5, 15); (j)E(B_goods,r_B_goods)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(B_goods,r_B_goods)〈b〉) = (1, 3, 5, 15); (k)E(p3,r_money)〈b〉 = (s),fint(E(p3,r_money)〈b〉) = 2; (l)E(p13,s_B_money)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(p13,s_B_money)〈b〉) = (1, 3, 5, 15); (m)E(B_money,r_money)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(B_money,r_money)〈b〉) = (1, 3, 5, 15); (n)E(OB,tB)〈b〉 = (b1,b2,b1+b2),fint(E(OB,tB)〈b〉) = (3, 5, 15); (o)E(p4,end)〈b〉 = (s),fint(E(p4,end)〈b〉) = 2; (p)E(OS,tS)〈b〉 = (s),fint(E(OS,tS)〈b〉) = 2。 2)变迁的输出弧 (a)E(s_offer,p1)〈b〉 = (s),fint(E(s_offer,p1)〈b〉) = 2; (b)E(s_offer,B_offer)〈b〉 = (s),fint(E(s_offer,B_offer)〈b〉) = 2; (c)E(r_B_offer,p11)〈b〉 = (b1+b2),fint(E(r_B_offer,p11)〈b〉) = 15; (d)E(B_refuse,OB)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(B_refuse,OB)〈b〉) = (1, 3, 5, 15); (e)E(s_B_order,p12)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(s_B_order,p12)〈b〉) = (1, 3, 5, 15); (f)E(s_B_order,B_order)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(s_B_order,B_order)〈b〉) = (1, 3, 5, 15); (g)E(r_order,p2)〈b〉 = (s,s+b1,s+b2,s+b1+b2),fint(E(r_order,p2)〈b〉) = (2, 6, 10, 30); (h)E(s_goods,p3)〈b〉 = (s),fint(E(s_goods,p3)〈b〉) = 2; (i)E(s_goods,B_goods)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(s_goods,B_goods)〈b〉) = (1, 3, 5, 15); (j)E(r_B_goods,p13)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(r_B_goods,p13)〈b〉) = (1, 3, 5, 15); (k)E(s_B_money,OB)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(s_B_money,OB)〈b〉) = (1, 3, 5, 15); (l)E(s_B_money,B_money)〈b〉 = (Ø,b1,b2,b1+b2),fint(E(s_B_money,B_money)〈b〉) = (1, 3, 5, 15); (m)E(r_money,p4)〈b〉 = (s),fint(E(r_money,p4)〈b〉) = 2; (n)E(end,OS)〈b〉 = (s),fint(E(end,OS)〈b〉) = 2; (o)E(tS,iS)〈b〉 = (s),fint(E(tS,iS)) = 2; (p)E(tB,iB)〈b〉 = (b1,b2,b1+b2),fint(E(tB,iB)) = (3, 5, 15)。 图4 两个购买者流程的ECLPNEC可达树Fig. 4 ECLPNEC RT for two purchasers process 得到的可达树分别如图4、5所示,其中图4为两购买者流程的ECLPNEC可达树,B1和B2均从Seller购买。每个可达标识中有色托肯在库所中的分布如下: M0= {2, 15, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},M1= {1, 15, 2, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}, M2= {1, 1, 1, 15, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},M3= {1, 1, 1, 1, 2, 15, 15, 1, 1, 1, 1, 1, 1, 1, 1}, M4= {1, 1, 1, 1, 1, 1, 15, 30, 1, 1, 1, 1, 1, 1, 1},M5= {1, 1, 1, 1, 1, 1, 15, 1, 15, 1, 2, 1, 1, 1, 1}, M6= {1, 1, 1, 1, 1, 1, 1, 1, 1, 15, 2, 1, 1, 1, 1},M7= {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 15, 15, 1, 1}, M8= {1, 15, 1, 1, 1, 1, 1, 1, 1, 1, 2, 15, 1, 1, 1},M9= {1, 15, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1}。 M10= {1, 15, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2}。 图4中可达标识数量为10。图5为单购买者流程的ECLPNEC可达树,B1从Seller购买货物,B2不购买。为了降低可达树的规模,同时为了方便同CLPNEC比较,在构建ECLPNEC可达树(图5)的过程中应用下面的规则: 图5 单购买者流程的ECLPNEC可达树Fig. 5 ECLPNEC RT for one purchaser process 1)tB使能则优先引发。 2)s_B_order与B_refuse之间不能发生其他变迁。 3) 1)的优先级高于2)的优先级。 同理可得每个可达标识中有色托肯的分布,这里省略。图5中可达标识数量为14。由于无购买者与两个购买者的购买流程是等价的,故省略无购买者购买过程。通过表1中数据的对比,可以得到ECLPNEC与CLPNEC在模型规模上和可达树规模上的比较。 表1 CLPNEC与ECLPNEC比较Tab. 1 Comparison between CLPNEC and ECLPNEC 从表1可得,ECLPNEC的库所数、变迁数、模型有向弧数与两购买者、单购买者流程可达标识数,均明显小于CLPNEC,且ECLPNEC的规模大大降低。在拥有相同描述能力的基础上,ECLPNEC简化了模型结构。 改进颜色逻辑Petri网的定义,扩展了颜色逻辑网络系统的内容和方法,提出变迁的使能条件和引发规则。引入多重集类型的素数表示法,给出ECLPN可达树的构造算法,并用素数表示法给出判断变迁使能定理,定义了颜色逻辑关联矩阵,给出一步可达标识的计算公式以及可达树的构造方法。最后,针对一个电子商务实例,分别用CLPN方法和ECLPN方法构建模型与可达树并进行比较分析。分析结果例证了ECLPN在拥有与CLPN相同描述能力的同时,具有更加简洁的模型结构和较低的复杂度。下一步将研究ECLPN的静态和动态性质分析方法,如活性、公平性等,并给出更多的ECLPN应用领域。2.3 颜色逻辑关联矩阵与可达标识方程
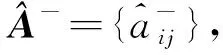

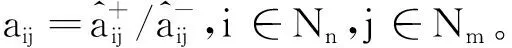

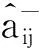
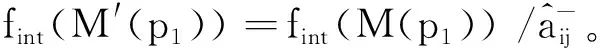
2.4 ECLPN的可达树
3 实例对比分析
3.1 电子商务实例
3.2 电子商务实例的模型CLPNEC
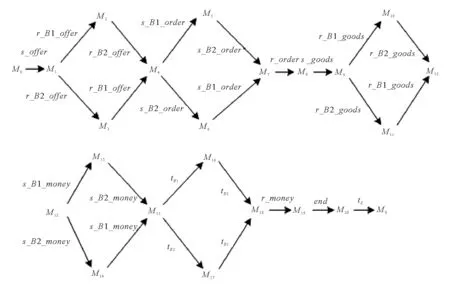
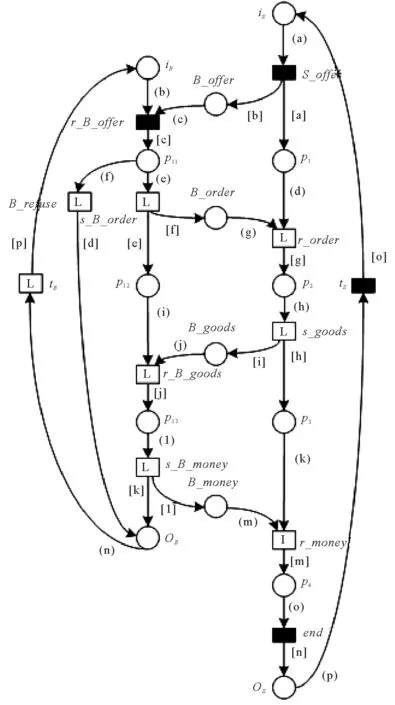
3.3 电子商务实例的模型ECLPNEC

4 结束语
