基于自适应神经模糊Petri网的电机故障诊断

2020-05-13程学珍王常安李继明许传诺

山东科技大学学报(自然科学版) 2020年3期

程学珍，王常安，李继明，许传诺

(山东科技大学电气与自动化工程学院，山东青岛 266590)

电机系统是由多数量功能模块组成的系统，其故障往往呈现不确定性以及非线性的特征，任意功能模块的微小偏差都可能导致整个系统的崩溃[1]。因此为其寻找一种合理、有效的故障诊断方法至关重要。

目前电机的故障诊断方法主要包括定量分析和定性分析两类。其中定量分析方法包括基于解析模型方法和数据驱动方法。目前常用定量分析的数据驱动方法对电机系统中转子以及轴承的故障特征信号进行处理。文献[2]将Prony方法与选带细化技术相结合，对转子断条故障特征频率附近的小频段进行局部放大分析，提高了计算的准确性，但是在低噪背景下，其诊断结果难以令人满意；文献[3]提出一种改进矩阵束滤波与检测的转子故障诊断技术，通过改进的矩阵束算法，有效克服了噪声的影响，对短时数据具有较好的分辨能力。文献[4]提出利用Park矢量模变换技术与旋转不变信号参数估计技术，通过Park矢量模变换技术消除工频分量的影响，在保证准确性的前提下，减少了计算量。文献[5]提出一种基于小波变换和希尔伯特变换相结合的电机轴承故障诊断技术，通过希尔伯特变换解调调制信号，实现对故障特征信号的有效分析，同时该方法在小波变换中引入Thselect函数，利用函数的自适应能力，调节不同噪声情况下的阈值大小，实现消除高频信号的功能，提高了算法的自适应能力，但是该方法忽略了低频信号的噪声干扰，仍然会导致误判漏判的现象。基于数据的定量分析方式虽然可以根据特征分量进行故障分析，但是在电机系统中，故障检测的准确性往往会受到干扰信号的影响而降低，因此定量分析法难以满足电机系统故障诊断需求。

定性分析是依靠系统内部知识建立系统模型的一种方法[6]，主要有图论方法、专家系统和定性仿真等。其中Petri网是一种图论方法，可利用目标系统中元件关系来构建有向图的组合模型，准确地处理离散事件发生的顺序、并发和冲突的关系[7]。近年来随着国内外学者的研究，Petri网在电机系统故障检测中的应用逐渐增多，并且取得了较好的诊断结果。文献[8]针对故障传播过程中的不确定性，定义了故障Petri网的概率变迁方法，解决了以往Petri网故障诊断过程只关注库所状态的弊端，但是其概率变迁的方式不具备自适应能力。文献[9]提出构建修正状态类图，充分利用Petri网在实时系统中的重要作用，结合系统各执行机构建立可观的Petri网。文献[10-11]运用有色Petri网和建模工具CPNTools建立了有色Petri网模型，提高了故障诊断的效率和模型的直观性。文献[12]将Petri网和模糊推理相结合，有效的解决了一部分随机性、不确定性的故障问题，极大提高了故障诊断过程中定位故障源的能力。文献[13]对模糊Petri网(fuzzy Petri net，FPN)进行了严谨的数学推理，给出了矩阵化的推理过程，对FPN的应用和发展奠定了坚实的理论基础，但其权值的获取仍然依靠专家经验，适应性较差。

为克服以往FPN准确性和自适应能力差的问题，提高算法对电机系统故障诊断的能力，本研究提出了基于神经模糊Petri网(neural fuzzy Petri net，NFPN)的故障诊断方法，其创新性如下：

1) 使用失效模式与影响分析方法对故障数据进行处理，解决了初始参数赋值经验化的问题。

2) 引入高斯函数代替变迁可信度，通过变迁影响因子反映变迁对其输出库所的影响能力。

3) 通过BP神经网络算法(back propagation neural network，BPNN)对权值和变迁影响因子进行学习训练，提高算法的自适应能力。

通过仿真验证本研究所提出的算法能准确地诊断三相异步电动机的故障，具有较好的准确性和适应性，可有效提高电机的检修和维护效率。

1 神经模糊Petri网

1.1 BP神经网络

BP神经网络是具有前向传播和误差反传两种工作模式的智能算法，其中前向传播反映了系统的运行过程，误差反传反映了对系统准确度的调节过程。通过两种工作模式，BP神经网络可以根据输入输出值找到系统的相关规则，并依据该规则在实际运行过程中准确推导输出，具有较好的非线性映射能力，因此被广泛应用于电机系统的故障诊断。

1.2 NFPN的定义

在电机系统中，故障的发生充满了不确定性，导致提取的故障信息具有模糊特性。而传统Petri网并不能处理该类型的数据，文献[14]将模糊理论引入到Petri网中得到FPN，并将其应用于三相异步电动机的故障诊断。与传统Petri不同，FPN清晰地反映出系统中各部件的状态信息量，能够满足模糊事件的处理需求。

根据FPN理论和BP神经网络算法的特性，定义NFPN为一个9元组：

SNFPN=(P,T,I,O,M,W,α,F,B)。

1)P={p1,p2,…,pn}T，表示库所的集合。

2)T={t1,t2,…,tm}，表示变迁的集合。

3)I为输入矩阵，描述库所到变迁的映射。对于输入矩阵元素δij={0,1}，当pi是tj的输入时，δij=1；当pi不是tj的输入时δij=0，其中i=1,2,…,n;j=1,2,…,m。

4)O为输出矩阵，描述变迁到库所的映射。对于输入矩阵元素γij∈{0,1}，当tj是pi的输入时，γij=1；当tj不是pi的输入时，γij=0，其中i=1,2,…,n;j=1,2,…,m。

5)M=(m1,m2,…,mn)，表示库所标识分布向量。

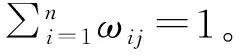
7)α=(α1,α2,…,αn)，αi∈[0,1]，表示库所pi所代表故障事件的置信度。

8)F={f1,f2,…,fn}，为库所最小割集故障发生率的集合。

9)B=(b1,b2,…,bm)，表示变迁对其输出库所的影响能力，bi为变迁影响因子。

2 NFPN的学习与诊断

为提高FPN的自适应能力，本研究在FPN的基础上结合BP神经网络给出了NFPN的定义。同时，结合BP神经网络算法的自学习能力，对权值和变迁影响因子进行训练，提高算法的适应性和准确性。

2.1 NFPN故障诊断

在电机系统中，设备自身的物理结构与故障、设备的故障与故障之间都存在着多重映射的关系，故障在传播过程中存在着冗杂性与多样性，并伴随着多种传播模式。

为体现NFPN算法解决上述复杂故障传播模式的能力，清晰的展现出NFPN算法的推理过程与并行处理的特点，提高算法的适应性。定义如下3个算子:

2) 取大算子⊕:C=A⊕B，A，B和C均为m×n矩阵，cj=max(aij,bij),i=1,2,…,m；j=1,2,…,n。

3) 直乘算子⊗:C=A⊗b，A为m×n矩阵，b为m维向量，则cij=aij·bi，i=1,2,…,m；j=1,2,…,n。

借助上述算子定义，进行演绎推理计算：

1) 置信度推理

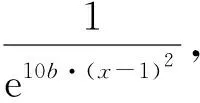
(1)

根据NFPN算法故障推理结果的要求，αk+1=αk时，推理结束，否则继续由αk推导得到αk+1，α0为系统规定的初始值。

2) 变迁点火判别

定义：X=(x1,x2,…,xm),X为具有标识的库所置信度与对应权值乘积等效和的m维向量。

Xk=(αk*Mk)·W。

(2)

为判别变迁使能情况，引用Sigmoid函数:

(3)

其中，c为正无穷大，λ为变迁阈值,Sk=(s1,s2,…,sm)为变迁的预使能矩阵，使得当x≥λ时，满足点火条件s(x)=1；当x<λ时，s(x)=0。

3) 故障传播推理

NFPN的故障推理过程反映了系统故障的传播方向，其中托肯反映了系统故障发生的情况，随着变迁点火，托肯将由输入库所传递给其输出库所。在Petri网中托肯的分布称为库所标识，用向量M表示。故障传播推理公式为：

(4)

其中,Mk+1的变化反映了库所中托肯的变化，M0为给定的系统初始值。

2.2 NFPN故障预测

NFPN故障诊断是在已知故障结果的情况下，对引起故障的原因进行诊断，在相应模型中，快速定位故障位置。同时为准确预测故障的具体位置，在NFPN故障诊断结束时，加入最小割集发生率，对引起故障的所有底层库所(即最小割集)进行排序，检修人员可以根据最小割集发生率的大小依次对底层库所进行排查，避免了维修的盲目性，提高了维修效率。

故障预测公式为：

(5)

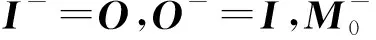
若最小割集为F={f1,f2,…,fn}，则最小割集障发生率为[15]：

(6)

2.3 NFPN的自学习能力

在FPN中，权值反映了输入库所对其变迁的影响程度，变迁可信度反映了变迁对其输出库所的影响程度。在故障传播过程中，这两个值共同反映了故障的传播能力。但是在电机系统中，故障由变迁传递给输出库所的过程往往是非线性的，为准确反映故障的传播能力，利用高斯函数代替经验化严重的变迁可信度，通过改变变迁影响因子模拟实际情况下故障传播的过程。同时为提高FPN在电机系统的自适应能力，引入BP神经网络，利用神经网络的误差反传方式对权值ω和变迁影响因子b进行调节，提高算法的适应性和准确性。基于BP神经网络的自适应学习流程如图1所示。

图1 基于BP神经网络的自适应学习流程图

定义误差函数为[16]：

(7)

式中α(pi)为输出库所实际置信度值，αE(pi)为输出库所期望置信度值。权值的修改量梯度为：

(8)

(9)

(10)

(11)

变迁影响因子的修改梯度为：

(12)

(13)

(14)

3 三相异步电动机的数据处理与模型构建

3.1 故障数据处理

三相异步电动机内部结构复杂，引起故障的原因多样。为准确提取三相异步电动机的故障特征并建立符合实际的故障模型，采用失效模式分析和FPN相结合的方式分析故障数据并建立符合电机系统的故障关系表[28]。其中库所代表的故障含义如表1所示。

表1 库所故障对应表

3.2 三相异步电动机NFPN模型的建立

通过对三相异步电动机的结构与故障的分析，在Labview软件上建立如图2所示的三相异步电动机NFPN模型[17]。

4 方法的实现

以“电机绕组绝缘烧毁”、“电机抱轴”为例进行推理分析。

4.1 基于BP的初值确定

参照模糊理论、Petri网理论和历史统计数据等，对数据进行了相应的处理与规范，并借助专家经验设定初始库所置信度、权值、阈值与变迁影响因子。

库所初始置信度：

α0=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0.9,0,0)。

变迁阀值设为0.5。

权值初始值ω1,2=0.4，ω2,2=0.6，ω2,3=0.3，ω3,3=0.5，ω4,3=0.2，ω9,9=0.6，ω10,9=0.4，ω12,12=0.31，ω13,12=0.69，其余权值为1。

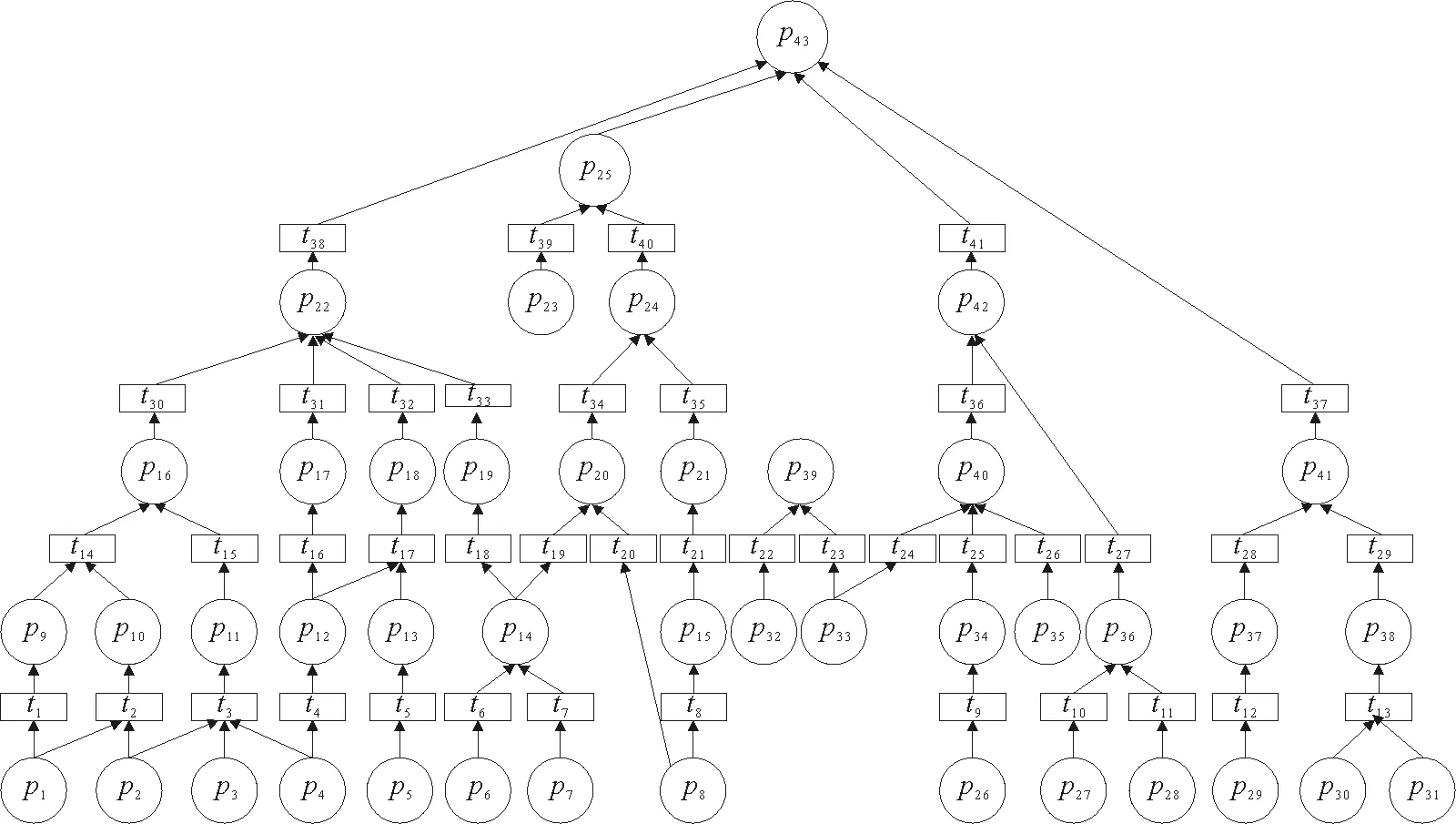
图2 基于Labview的三相异步电动机NFPN模型

变迁影响因子初始值均设为0.3。

同时，利用BP神经网络的误差反传功能对初始权值和变迁影响因子寻优。为清晰的展现BP神经网络对权值及变迁影响因子的训练，以输入库所p1、p2、p3、p4影响输出库所p10、p11的过程为例，其库所置信度的期望值为αE(p10)=0.667，αE(p11)=0.732，最大学习步数设为t=2 000，学习率η=0.1，E的最大允许误差为1×10-3。经过训练得到图3～5，分别代表最大允许误差曲线、权值训练曲线和变迁影响因子训练曲线。

图3 p9、p10的误差曲线

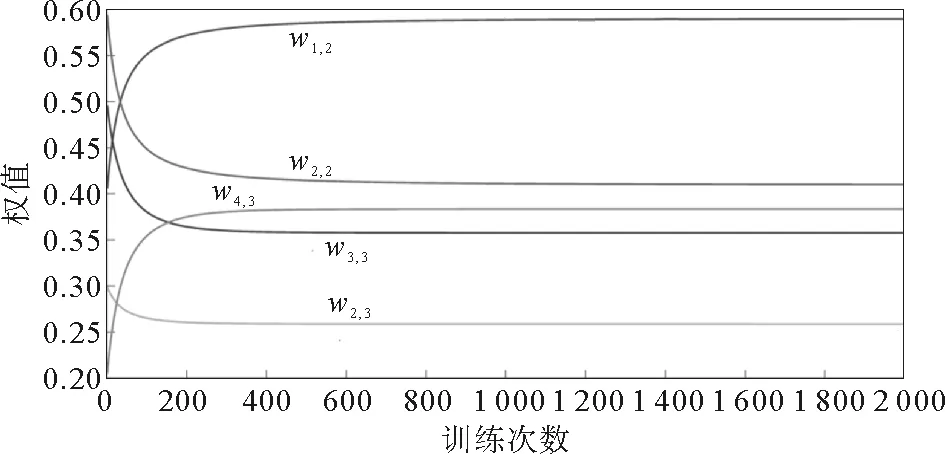
图4 权值训练曲线

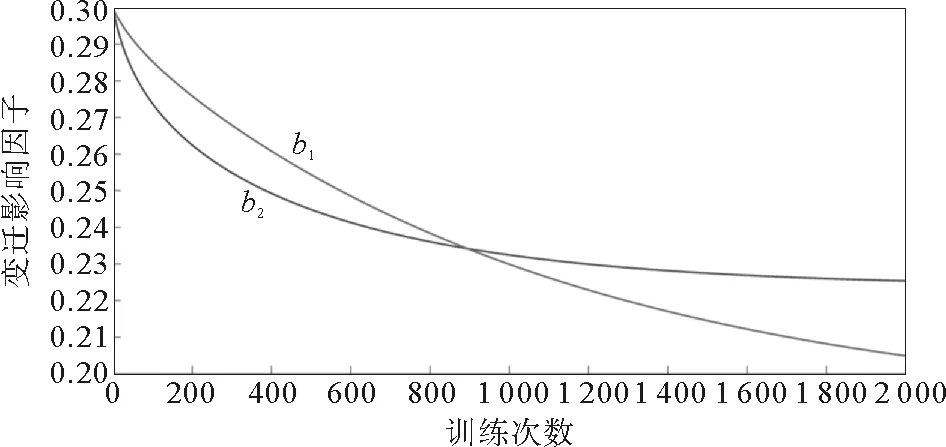
图5 b1、b2的变迁影响因子曲线

从图中可以看到在2 000次迭代之后，E1、E2均小于最大允许误差1×10-3，结果符合要求。通过训练最终得到调节后的权值:ω1,2=0.590，ω2,2=0.410，ω2,3=0.259，ω3,3=0.358，ω4,3=0.383，ω9,9=0.554，ω10,9=0.446，ω12,12=0.483，ω13,12=0.517。调节后的变迁影响因子为：

B=(0.275,0.225,0.205,0.292,0.176,0.260,0.294,0.260,0.226,0.276,0.246,0.282,0.193,0.228,0.292,0.200,0.247,0.278,0.140,0.208,0.223,0.289,0.291,0.270)。

4.2 故障诊断

假设检测到“转子绕组短路”、“电机负载过大”、“熔断器熔体故障”、“轴封环结构损坏”、“油封材料过热”等故障。

在此初始标识为M0=(0,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)。

根据故障诊断要求，当αk+1=αk时推理结束，αk为最终的库所置信度向量。

α4=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0.069,0.727,0.859,0.642,0.848,0,0.592,0.818,0.624,0.811,0.804,0,0.752,0.9,0.738,0.613)，

M4=(0,1,1,1,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1,0,1,0,1,1)，

S4=(0,0,1,1,1,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1)，

α5=(0.87,0.6,0.83,0.89,0.73,0.88,0.72,0.82,0,0.069,0.727,0.859,0.642,0.848,0,0.592,0.818,0.624,0.811,0.804,0,0.752,0.9,0.738,0.613)，

M5=(0,1,1,1,1,1,0,0,0,0,1,1,1,1,0,1,1,1,1,1, 0,1,0,1,1)，

S5=(0,0,1,1,1,1,0,0,0,1,1,1,1,1,0,0,1,1,1,1,1,0,0,1)。

当α5=α4时推理结束，得到故障诊断信息，其中库所置信度的值表示该故障可能发生的概率，可以有针对的进行检查。

4.3 故障预测

当电机出现故障，需要工作人员排查维修时，需要进行故障诊断。假设出现p22即“电机绕组绝缘烧毁”故障。经过推导当M3-=M4-时，推理结束。得到：

M3-=(1,1,1,1,1,1,1,0,1,1,1,1,1,1,0,1,1,1,1,0,0,1,0,0,0)。

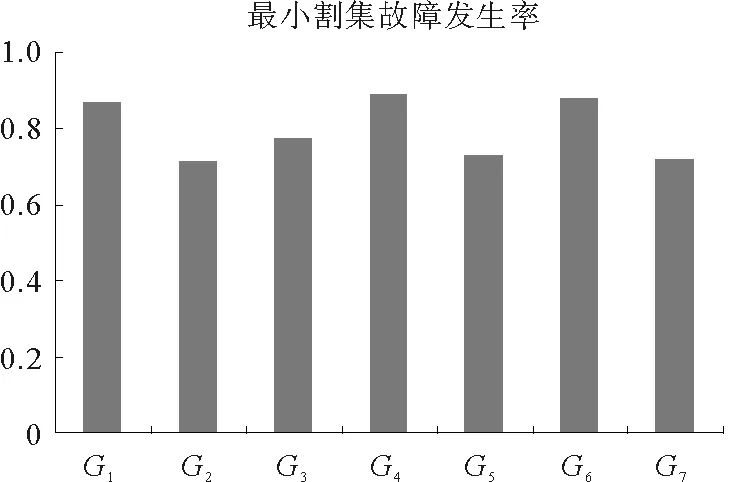
图6 最小割集故障发生率

推理结束后，采用2.2中所述的最小割集计算方法，来计算P22“电机绕组绝缘烧毁”的最小割集。其割集为：G1={p1}，G2={p1,p2}，G3={p2,p3,p4}，G4={p4}，G5={p5}，G6={p6}，G7={p7}。根据式(6)，得到各个割集的发生率G1=0.87，G2=0.735，G3=0.773，G4=0.89，G5=0.73，G6=0.88，G7=0.72。各个最小割集发生率对应的柱状如图6。

在三相异步电动机发生故障时，可根据最小割集故障发生率来依次排查，有效地避免了维修的盲目性并提升诊断的速度。在此实例中，排查的顺序为G4，G6，G1，G3，G5，G7，G2。

5 方法的验证

5.1 有效性验证

为验证算法的有效性，引入故障树方法对三相异步电动机故障诊断的推理结果有效性进行验证[18]。其中故障树中各个事件所代表的故障含义如表1所示。在此，以“转子绕组短路”、“电机负载过大”、“熔断器熔体故障”为例进行验证对比。首先，建立“电机运行过热”故障树如图7。

将库所置信度、权值、阈值和Petri网触发规则引入故障树。根据触发规则，其中X1×ω1,2+X2×ω2,2=0+0.6×0.41=0.246<0.5，不满足变迁触发条件，X5不被触发。需要注意的是，依据Petri网特性，X5与X6组成的与逻辑和X7为竞争关系，需要选取其中的最大值。最后推导得到X8的置信度，X8=0.592，计算结果与NFPN的计算结果相吻合，证明本算法的有效性。

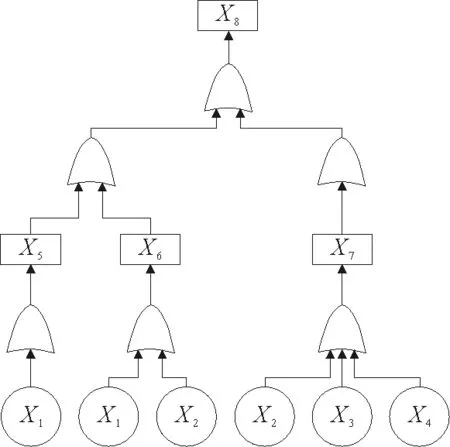
图7 电机运行过热故障树

5.2 准确性验证

为验证算法的准确性，与文献[18]中的算法进行对比，结果如表2所示。

由表2的结果对比可以发现，FFPN和NFPN算法都可以准确地诊断出故障位置，相比于FFPN诊断算法，本算法的故障诊断结果具有更好的准确性；同时，故障诊断参数经过BP神经网络算法的调整，保证了不同故障情况下的检测准确性均在80%以上，克服了FFPN算法由于赋值经验化导致适应性差的问题。因此，通过上述比较可以证明本研究所提出的方法能够满足电机系统的故障诊断要求。