基于二维模型预测控制的迭代学习控制性能评估方法
2020-05-13王永耀索寒生孙希法
王永耀,索寒生,王 娟,孙希法
(1.中国石油化工集团有限公司 信息和数字化管理部,北京 100728;2.石化盈科信息技术有限责任公司 信息技术研究院,北京 100007;3.北京化工大学 信息技术研究院,北京 100029;4.北京时代凌宇科技股份有限公司,北京 100012)
为实现工业生产中的批次过程更好地运行,研究人员在批次生产控制方面做了大量的研究工作,迭代学习控制(iterative learning control,ILC)能够充分挖掘重复信息,是处理批次过程的有力工具。由于缺乏足够的维护、设备老化、传感器/执行器故障等原因[1],控制器的性能会随着时间的推移逐渐下降,监测和评定控制器性能的性能评估技术应运而生[2]。然而,针对迭代学习控制的性能评估研究不多;同时,由于批次过程的周期性或重复性,针对一般系统的性能评估方法不适用。因此,迭代学习控制性能评估研究对推动工业发展具有重要意义。
1978年,迭代学习控制的概念首次出现在文献[3]中。1984年,Arimoto等[4]首次发表了ILC方面的研究论文。1990年,Geng等[5]成功地将二维系统理论应用于离散系统的迭代学习控制的设计,在此之后大批学者参照这个思路进行了研究[6]。二维系统是能够同时在两个独立的方向上演化的动态系统[7],考虑到迭代学习控制的更新恰好同时包括时间轴和批次轴,因此可以把迭代学习控制作用下的闭环系统转换成二维系统,从而达到简化研究的效果。
控制性能评估(control performance assessment,CPA)技术可以有效解决控制性能欠佳的问题,因而在学术界和工业界引起广泛的关注[8]。控制性能评估的相关研究最早可以追溯到1970年[9]。1989年,Harris在最小方差控制的背景下引出名词性能指标(Harris指标)[10],象征着CPA的兴起。大批学者致力于拓展此领域,并取得了突破性进展。Huang等[11]为简化最小方差基准计算,提出使用滤波相关法进行估计。最小方差基准由于过于理想化,其他更贴近实际的性能评估基准被陆续地设计出来。Huang等[12]基于线性二次高斯控制器设计了线性二次高斯(linear quadratic Gaussian,LQG)基准——展现为一条性能权衡曲线,LQG基准比最小方差控制(minimum variance control,MVC)基准更贴近实际。Zhao等[13]将LQG基准应用到先进过程控制的经济性能评估。Julien等[14]提出了模型预测控制(model predictive control,MPC)基准,已在工业界有很多成功的应用案例,是目前最实用的先进控制方法。
虽然性能评估技术成果颇丰,但有关迭代学习控制的评估研究报道较少。直到2009年,Chen和Kong的工作[15]弥补了这一缺憾,以最小方差控制为基准对ILC进行性能评估。2013年,Farasat和Huang指出文献[16]遗漏了确定性性能与随机性性能之间的耦合关系,通过把系统划分为内环控制器和外环控制器,同时加入权重系数,提出了一个更全面的方案。2015 年,Wei等[17]选用线性二次高斯基准构建了一个全新的评估工具——性能评估曲面。接着,Wang等[18]继续对该理论进行深入研究,进一步将一维基准控制器改进为二维基准控制器。随着迭代学习控制在工业过程中的地位越来越重要,亟需更好的框架来评估其性能。
本研究利用二维系统理论,首次为迭代学习控制设计MPC基准的性能评估策略。针对工业过程通常模型未知的问题,设计了闭环子空间辨识方法,进而得到数据驱动的评估策略。算法可以概括为:根据测量得到的输入输出数据构造Hankel矩阵,再借助正交三角分解(QR decomposition,QRD)、奇异值分解(singular value decomposition,SVD)等几何工具计算出子空间矩阵[19],由列子空间与行子空间估计出系统模型参数。在得到辨识模型后,把迭代学习控制作用下的闭环系统转换成二维模型,进而设计基于二维MPC基准的控制性能评估策略。设计方法在注塑过程上进行了仿真测试。
本研究的主要创新在于:为迭代学习控制设计了二维MPC基准的性能评估策略;针对工业过程通常模型未知的问题,首次设计了数据驱动的评估策略;对Fornasini-Marchesini(FM)模型参数的获取进行了深入研究。
1 子空间辨识
汉克尔矩阵(Hankel matrix):

托普利兹矩阵(Toeplitz matrix):

由于子空间辨识是基于投影的算法,接下来将介绍其中涉及到的正交投影理论:
任意矩阵的行空间映射至矩阵Φ的行空间上的算子记为:
∏Φ=ΦT(ΦΦT)†Φ,
(1)
其中,符号†代指伪逆,在MATLAB中,调用函数pinv即可求得。
在此基础上,可以得到Ψ/Φ=Ψ∏Φ=ΨΦT(ΦΦT)†Φ。
类似地,任意矩阵的行空间映射至矩阵Φ的行空间正交补上的算子记为:
∏Φ⊥=Ι-∏Φ,
(2)
则有
Ψ/Φ⊥=Ψ∏Φ⊥。
借助∏Φ和∏Φ⊥,能够把Ψ拆分为下列形式:
Ψ=Ψ∏Φ+Ψ∏Φ⊥。
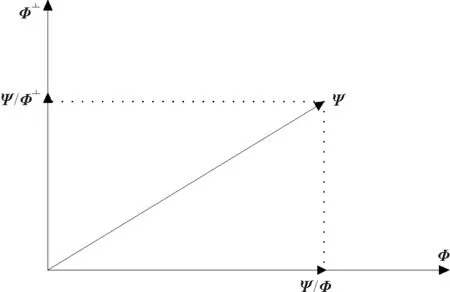
图1 矩阵正交投影过程的图像化展示
如图1所示。
2 二维子空间矩阵
考虑如下批次过程:
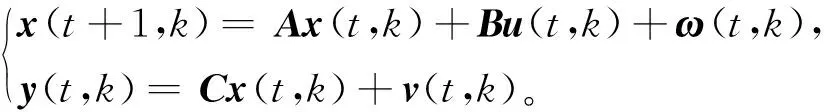
(3)
其中,t=0,1,…,T-1,为时间指标;k=0,1,…,N-1为批次指标;x∈Rn、u∈Rp以及y∈Rm分别表示状态、输入和输出;ω∈Rn与v∈Rm皆为高斯白噪声,分别指系统噪声、测量噪声。
对于上述批次过程,引入如下形式的迭代学习控制律:
∑ILC:u(t,k)=u(t,k-1)+r(t,k)。
(4)
其中,r(t,k)是待设计的学习律。
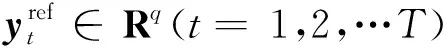
(5)
为了在二维系统理论框架下进行推导,定义符号:
(6)
由式(3)~(6),可以得到如下所示的二维系统的典型描述形式——Fornasini-Marchesini(FM)模型:
(7)
(8)
把式(7)简化成:
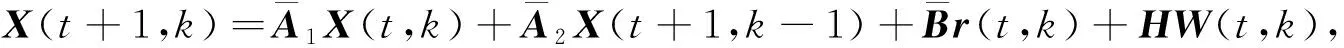
(9)
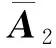
(10)
又注意到A1第二列矩阵块的元素都为0,所以作下列变形也不会造成影响:
(11)
考虑下列新息模型,可以看出是对式(11)的一般化形式:
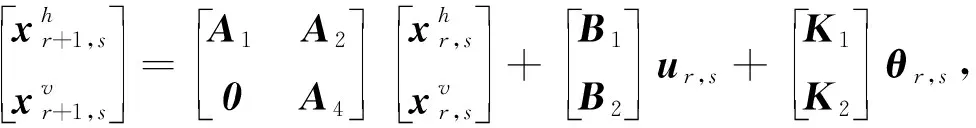
(12)

根据Ramos等学者的理论,对式(12)进行反复的迭代操作,最终获得下述子空间等式:
(13)
(14)
(15)
其中,下标p指过去项、f指未来项,输入Hankel矩阵Up和Uf定义如下:

输出Hankel 矩阵的具体表达式为:

状态矩阵定义如下:
扩展的可观测矩阵以及扩展的可控矩阵的具体表达式分别为:
下三角托普利兹矩阵为:
上述过程是为闭环子空间辨识做准备,下一节借鉴文献[20]的子空间模型辨识主元分析(subspace model identification-principal component analysis,SIM-PCA)思想,面向开环系统的二维子空间辨识,推导出带有扰动闭环的方法。
3 闭环子空间辨识
(16)
接着,做一些简单的变形:
(17)
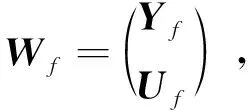
(18)
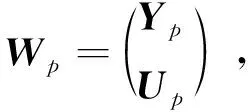
(19)
(20)
(21)
记Z=Wf/Wp,对Z做SVD分解:
(22)
结合式(21)和式(22),可以看出Z的正交列空间等于U2,则有
(23)
其中,M可以取作任意的常数非奇异矩阵。
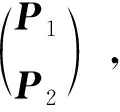
(24)
由式(24)可以得到:
(25)
(26)
4 控制性能评估
根据第3节中的算法,可以获得系统矩阵A、B、C、D,进而得到系统(9)。为该二维系统设计控制器:
r(t,k)=K1X(t,k)+K2X(t+1,k-1)。
(27)
实际上,这种情况下的二维控制器设计可以分解为状态反馈控制和前馈ILC控制。状态反馈控制用来提高系统状态的收敛性能,而前馈ILC控制则用于保证沿批次方向的收敛性。
结合式(9)和式(27),可以得到以下形式:
(28)
定义二维MPC代价函数:
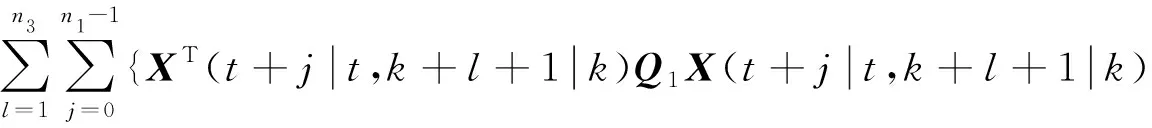
+XT(t+j+1|t,k+l|k)Q2X(t+j+1|t,k+l|k)
+(r(t+j,k+l+1))TMr(t+j,k+l+1)}}
(29)
其中,φT(j,l)=[XT(t+j|t,k+l+1|k),XT(t+j+1|t,k+l|k)],Q1,Q2,M是权重矩阵。
MPC基准控制器可以通过求解下列优化问题获得
(30)
但一维MPC控制问题的解决方案不能直接应用于二维系统,因为两个系统的结构和动态复杂性有着显著的差别。为此,本节提出了一个次优的解决方案。在证明主要结论的过程中,需要用到下面两个引理。
引理1[21]对于具有适当维度的给定矩阵W,L和V,其中W和V是正定矩阵,满足
LTVL-W<0。
(31)
当且仅当
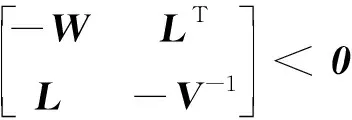
(32)
引理2[22]设E、G、F和M表示具有适当维度的实矩阵,M满足M=MT,则对于所有GTG≤I,
M+EGF+FTGTET<0,
(33)
当且仅当存在μ>0满足
M+μ-1EET+μFTF<0。
(34)
定理1假设W(t,k)≡0成立。给定二维FM系统(9),则优化问题(30)是可解的,如果存在正定对称矩阵S1、S2、Ω以及矩阵Y1、Y2,满足
(35)
基于上述线性矩阵不等式(linear matrix inequality,LMI)的解,可以得到控制律的增益:
K1=Y1Ω-1,K2=Y2Ω-1。
(36)
证明:设计如下Lyapunov函数:
(37)
其中,[·]是任何具有适当维度的正定对称矩阵。对于正定对称矩阵P、R1、R2,有
ΔV(X(t,k))=Vp(X(t+1,k))-VR1(X(t,k))-VR2(X(t+1,k-1))
=‖X(t+1,k)‖p-‖X(t,k)‖R1-‖X(t+1,k-1)‖R2。
(38)
根据等式(28),可以得到:
(39)
对式(35)的左侧矩阵分别左乘和右乘对角矩阵diag{P,P,I,I,I,I},得到矩阵不等式(35)等价于
(40)
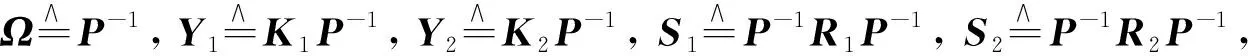
(41)
由此,可以得到
(42)
根据上式有:
(43)
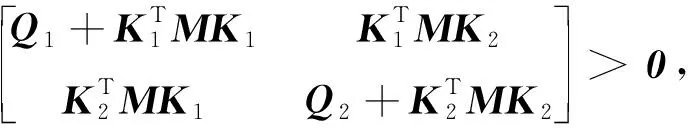
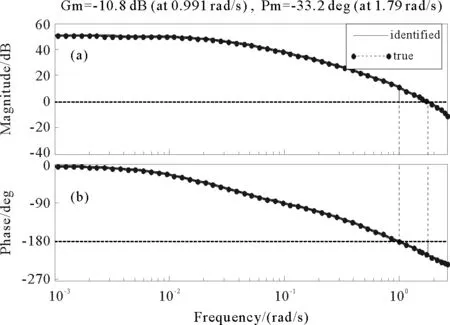
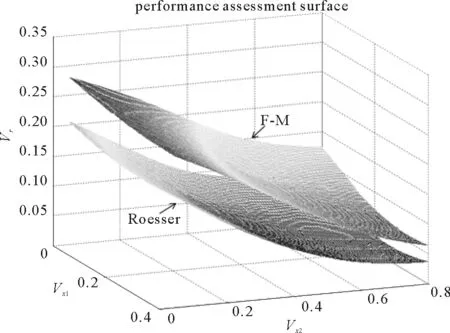
Vp(X(t+1,k)) (44) 不失一般性,假设R1=λP,R2=(1-λ)P,也就是说R1=P-R2,这带来 Vp(X(t+1,k)) (45) 对于任意整数T0,K0,i>0,以下不等式成立: Vp(X(T0+1,K0+i)) Vp(X(T0+2,K0+i-1)) +VR2(X(T0+2,K0+i-2), ⋮ Vp(X(T0+i,K0+1)) +VR2(X(T0+i,K0)。 把这些不等式相加,得到 很明显,Lyapunov函数值的总和沿状态轨迹逐渐减小,那么当系统批次趋向于无穷时,会完全跟踪期望轨迹。 证明完毕。 注塑成型是典型的批次过程,其注射阶段对注射速度的控制关乎产品质量的高低。本节选用注塑过程的注射阶段作为研究对象,通过仿真实验来验证设计的算法。 已经确定相对于比例阀的注射速度被描述为如下模型[23]: (46) 上述传递函数模型可以转换成下列状态空间模型: (47) 在仿真中,首先假设模型参数是未知的,使用上述模型生成的数据来验证所提出的闭环子空间辨识方法。为此,进行了30次仿真实验,并从不同角度展示了识别结果。 图2 系统矩阵A的特征根 图3 真实模型和识别模型的波德图 表1 特征值的平均值和方差 图2描述了系统矩阵A的真实特征根和利用子空间算法识别出的特征根,经过对比可知辨识效果较为理想。同时,表1中的数据也表明,特征根的平均值和方差皆处于可接受的范围内。图3是真实模型和辨识模型的Bode图比较。综上所述,所识别的效果实现了一致的估计和良好的准确性。从而,可以进行下一步的性能评估研究。 该系统的控制目标是跟踪以下参考轨迹: (48) LQG基准对应的代价函数通常选取: (49) 根据已有的求解LQG问题的算法,就可以得到r(t,k)的最优解;然后就能够拟合出性能曲面。为了对比两种基准的评估效果,将它们分别作为评估模型(47)的基准,并将各自的性能曲面展示在同一个仿真图(图4)中。 由图4可看出,MPC基准对应的性能曲面要高于LQG基准对应的性能曲面。造成这种局面的原因有两个:第一,过程模型的精确度不能百分百保证,在设计模型预测控制器时经常采用与实际模型不匹配的近似模型。第二,两者优化目标中的时间范围不同:MPC的优化目标是有限时域,而LQG是无限时域。因此,即使过程和扰动模型精确已知,MPC性能曲面也一定高于LQG性能曲面。 图4 两种基准下的性能曲面比较 本研究提出一种基于二维模型预测控制的迭代学习控制性能评估方法。考虑到实际的工业过程中通常无法知晓系统的模型,对如何获取FM模型参数展开了研究。为了保证安全、产品质量、系统稳定运行等,只能在闭环条件下进行辨识,由此提出了子空间辨识算法,所识别的效果实现了一致的估计和良好的准确性。在得到辨识模型后,把迭代学习控制作用下的闭环系统转换成二维模型,进而设计基于二维MPC基准的控制性能评估策略,其性能曲线高于LQG基准曲线。算法的仿真测试结果验证了其有效性。5 仿真实例
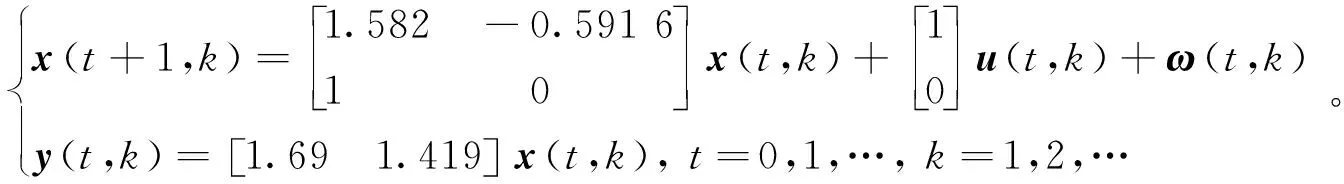



6 结论
