非理想网络环境下永磁同步电机转速鲁棒控制

汪石川，祝小元*，李豆豆，张桂臣

(1. 上海海事大学商船学院，上海 201306； 2. 上海海事大学信息工程学院，上海 201306)

永磁同步电机(PMSM)是一种典型的多变量强耦合的非线性系统[1]，工程上一般采用矢量控制技术实现PMSM的解耦控制，但其性能易受到外界扰动及内部参数变化的影响[2].电机运行时会受到外界扰动的影响，如当负载发生变化时，电磁转矩和负载转矩瞬间失衡，造成转速调节有一定的滞后.为减弱负载扰动对电机调速系统稳定性的影响，荀倩等[3]提出了一种负载转矩观测器，引入转矩电流的前馈补偿，提高电机转速环鲁棒性.LU等[4]使用反电动势观测器和扭矩观测器，分别估计转子位置和补偿负载转矩扰动.MU等[5]引入干扰观测器作补偿以抵抗干扰并降低控制增益，提高了响应速度.由于矢量控制建立在电机的动态数学模型基础之上，对电机参数的依赖性较强.为降低参数扰动对矢量控制稳定性的影响，韩秉哲[6]设计了PMSM伺服系统抗扰动控制器，抑制了转动惯量变化对控制性能的不利影响.邹权等[7]采用扰动观测器估计系统参数变化，减小了模型不确定性对系统控制性能的影响.

随着网络化技术的发展，控制器局域网络(CAN)被广泛应用于工业自动化系统中，有效降低了硬件系统的复杂程度.然而，日益增多的信号传递需求与网络带宽限制之间的矛盾极易诱发网络时滞，对控制系统的性能与稳定性造成了影响.ZHANG等[8]、帅志斌等[9]提出了时滞环境下提高车辆运动控制可靠性的方法.MOHMMAD[10]、ZHU等[11]通过构造Lyapunov-Krasovskii函数得出了时滞系统稳定性条件.MOHMMAD[12]则基于鲁棒控制方法提高了时滞情况下PMSM调速稳定性.对于通信时滞扰动对网络化控制的影响，已有一定的理论研究基础，但针对非理想网络环境下PMSM这一多变量强耦合系统的控制，可参考文献相对较少.此外，目前的研究对网络时滞的分析大多基于比较简化的模型，不能很好地反映由通信网络阻塞诱发不确定时滞的实际情况.

文中在网络环境下建立永磁同步电机时滞动力学模型，通过构造Lyapunov-Krasovskii函数，得出永磁同步电机调速控制系统稳定性条件，并进一步利用LMI工具箱计算出相应的鲁棒控制器增益.为验证控制器性能，在MATLAB/Simulink中建立基于CAN总线的PMSM调速控制系统模型，引入干扰信号造成CAN通道阻塞，以真实反映通信网络出现的不确定时滞.对比仿真结果验证鲁棒控制器的有效性.

1 永磁同步电机动力学建模与时滞

1.1 永磁同步电机动力学建模

依据同步旋转坐标系d-q下的永磁同步电机数学模型，运用id=0控制策略, 即令定子电枢直流分量的电流期望值始终为0, 避免了状态空间模型中出现耦合项.对于标贴式三相PMSM，定子电感满足Ld=Lq=Ls.此时永磁同步电机模型为

(1)

式中:ud,uq为定子电压的d-q轴分量；id,iq为定子电流的d-q轴分量；ωm为转子机械角速度；R为定子电阻;np为电机极对数；J为转动惯量；B为摩擦系数；TL为负载转矩；Ld,Lq为d-q轴电感分量,等于定子电感Ls；ψf为永磁体磁链.

故永磁同步电机状态空间方程为

(2)

(3)

状态空间方程可修改为

(4)

式(4)满足标准线性系统方程

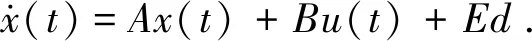
(5)

1.2 控制系统时滞分析

图1为基于CAN总线的PMSM控制系统结构框图，包含控制器、CAN总线及节点、逆变器和电机等受控对象这3个部分.控制器需要一定的计算能力，不宜安装在远程站点.逆变器和电机上的传感器监测电机运行状态参数，通过CAN总线将监测数据传输至驱动器.

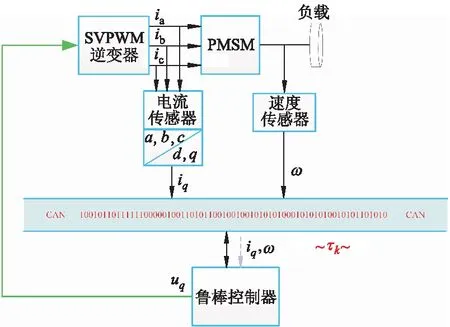
图1 基于CAN总线的永磁同步电机调速控制系统结构

Fig.1 Structure of permanent magnet synchronous motor speed control system based on CAN bus

为便于分析系统时滞并进行仿真计算，文中做出如下设定：① 传感器是以采样周期为h(h>0)的时间驱动的，PMSM电机的部分状态被封装成数据包通过节点传递至CAN总线，并传递至控制器.② 控制器是事件驱动的，数据包发送至控制器计算出控制量后，控制量被封装成数据包后经由CAN总线传递至电机等执行器，执行器也是事件驱动的，中间需由驱动模式转换模块.③ 由上所述，通信时滞包含控制器至执行器的延时和传感器至控制器的延时,分别用τca,τsc表示，总时滞时间τk=τca+τsc,且0≤τmin≤τk≤τmax≤h.

当通信时滞发生时，第kh(∀k∈N)次采样周期的数据到达控制器的时间为(kh+τk).

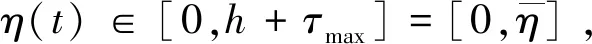
网络化PMSM调速控制系统状态空间方程可修改为

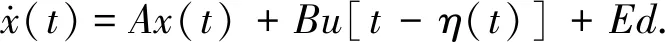
(6)

2 鲁棒控制器设计

图2为永磁同步电机伺服控制系统框图.伺服系统采用矢量控制方法，鲁棒控制器与PI控制器分别输出uq，ud，其中ud为定子电压的d轴分量.经过反Park变换、SVPWM算法后实现电机的转速控制.

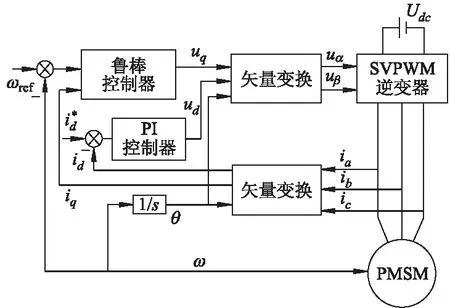
图2 永磁同步电机矢量控制框图

Fig.2 Block diagram of permanent magnet synchronous motor vector control

依据网络化PMSM调速控制系统状态空间方程，鲁棒控制器设计为

u(t)=Kx(kh),∀t∈[kh+τk,(k+1)h+τk+1],

(7)

式中：K为设计的状态反馈增益系数.

故网络化PMSM调速控制系统状态空间方程可写为

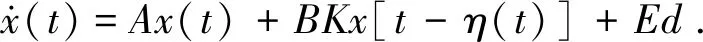
(8)

为设计满足非理想网络环境下PMSM调速控制的鲁棒控制器，需计算出控制器增益K，使通信时滞条件下伺服调速系统保持稳定.

(9)

(10)

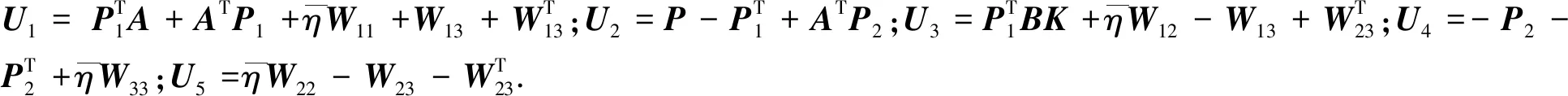
证明：构造Lyapunov-Krasovskii函数为

V=V1+V2+V3,

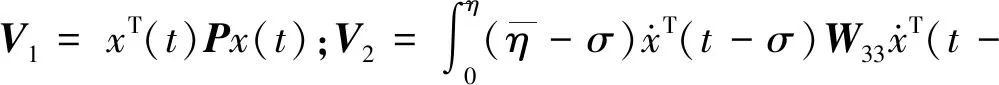
对V1，V2，V3求导得到

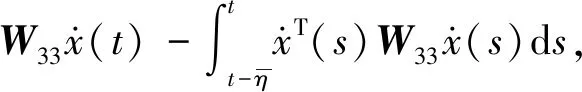
2xT(t)W13x(t)-2xT(t)W13x[t-η(t)]+

2xT[t-η(t)]W23x(t)-2xT[t-η(t)]·

2xT(t)W13x[t-η(t)]+2xT[t-η(t)]W23x(t)-

2xT[t-η(t)]W23x[t-η(t)]+

最终得到

(11)

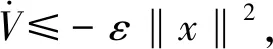
3 系统仿真结果及分析

为验证非理想网络环境下电机状态反馈调速控制系统的稳定性，如图3所示，在MATLAB/Simulink中建立基于CAN总线的PMSM调速控制系统仿真模型.其中CAN总线部分由节点、仲裁总线及干扰信号模块3部分组成[14].当通信网络发生阻塞时产生时滞，通信干扰模块中的信号发生器能够产生不确定时长的干扰信号，引入通信网络使通信时滞、系统响应时间拉长，以模拟网络通信量大的情况.

（四）创新阶段：打造共建共治共享的社会治理格局。2012年，党的十八大提出“要围绕构建中国特色社会主义社会管理体系，加快形成党委领导、政府负责、社会协同、公众参与、法治保障的社会管理体制”。首先，首次提出了要构建中国特色社会主义社会管理体系，并系统地阐述了社会管理需要“法治保障”，这一新内容表明社会管理要与法治相结合。其次，提出要把社会管理和社会建设统一起来，以“创新社会管理”来促进社会建设。最后，指出要加强创新社会管理体制，提高社会管理的科学化水平，积极鼓励社会主体参与到社会管理中来。

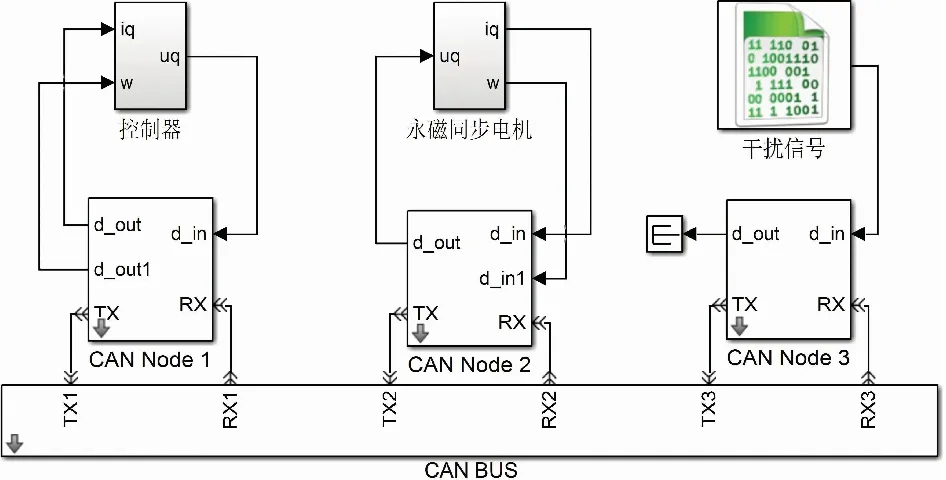
图3 基于CAN总线的PMSM调速控制系统仿真模型

Fig.3 Simulation model of PMSM speed control system based on CAN bus

图4为使用MATLAB/SimEvents模型库搭建的CAN总线节点仿真模型.

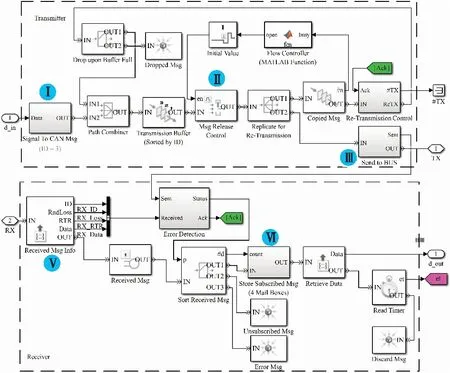
图4 CAN节点仿真模型

信号输入后经过① CAN Msg Generator模块打包成完整数据帧，根据回路传回总线状态.③ Msg release control模块判断是否发送消息.由④ Send to BUS模块发送到总线，而经由CAN总线传来的消息由⑥ Received Msg Info模块分解总线输入的数据帧，经过校验后只将发送给本节点的消息输出至⑧ Store Subscribed Msg消息缓冲模块.图5为CAN总线仿真模型.输入输出连接各节点的输入输出端，中间为仲裁机制部分.Block Upon Bus Busy开关模块根据Gate Controller子系统发来的CAN总线的状态，来判断是否发送消息.

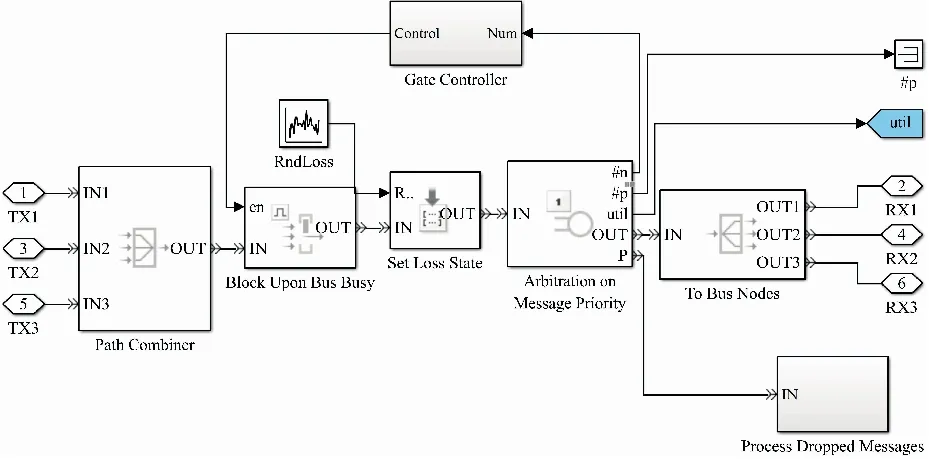
图5 CAN总线仿真建模

电机参数：极对数Pn=4，Ld=0.008 5 mH,Lq=0.008 5 mH，R=2.875 Ω，磁链φf=0.081 6 Wb,转动惯量J=0.000 8 kg·m·s，阻尼系数B=0.001 85 kg·m·s.参考转速nref=1000r/min,负载转矩TL=2 N·m.鲁棒控制器增益K计算结果为K=[-0.2924 0.6961].同时，与转速环、电流环均采用PI控制器的矢量控制方法对比[15].

转速环PI控制器表达式为

(12)

电流环PI控制器表达式为

(13)

式中:Kpw为速度环比例增益；Kpd,Kpq为电流环d-q轴比例增益；Kiw为速度环积分增益；Kid,Kiq为电流环d-q轴积分增益；Ba为阻尼系数；s为积分项.速度环PI控制器参数计算得到Kpω=0.003，Kiω=1.电流环Kpd=9.35，Kid=3162.5.

如图6所示，基于CAN总线的PMSM调速控制系统在通信正常时，鲁棒控制器与PI控制器在t=0.05s内均存在一定超调量，其中PI控制器虽控制结构简单，但受限于工程参数调整经验等因素，控制器参数难以调至最优控制效果.相较之下计算出控制器参数的鲁棒控制超调量较小，控制效果更优.而在t=0.05s后，2种控制器均能使系统稳定于目标转速、转矩，控制效果良好.

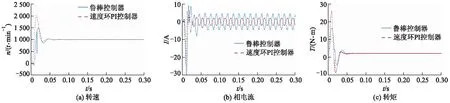
图6 通信正常时电机转速、转矩和相电流对比曲线

图7为CAN总线仿真模型通信时滞情况.

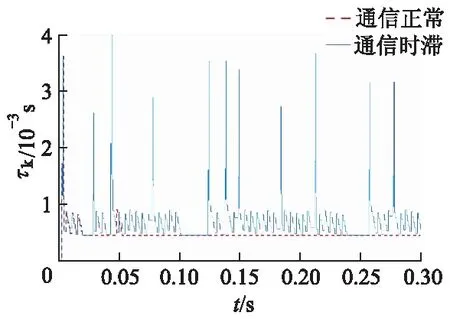
图7 通信时滞时间情况对比

通信正常时系统稳定时延较小，除去系统启动瞬间外，稳定在5.0×10-4s以内.引入干扰信号后产生不确定时滞τk<4.0×10-3s.

图8为非理想网络环境下电机转速(τk<4.0×10-3s)、转矩和相电流对比曲线.如图8所示，当干扰信号被引入系统后，延迟时间随机且大幅增加，导致基于PI控制器的调速系统丧失稳定性，始终无法稳定在目标值.而采用鲁棒控制器的调速系统，在t=0.1s前转速、转矩及相电流有一定波动，稳定速度较无时滞时有所延长，且仍然存在一定超调量.t=0.1s后系统趋于稳定，输出转速、转矩均能稳定于目标值，未出现波动情况，控制效果良好.综上所述，文中采用的PI控制器与鲁棒控制器均能满足通信正常时调速控制稳定性要求，但出现网络通信时滞后，PI控制器始终无法使系统稳定在目标值，出现了较大波动.而设计的鲁棒控制器效果良好，与无通信时滞时控制效果接近.

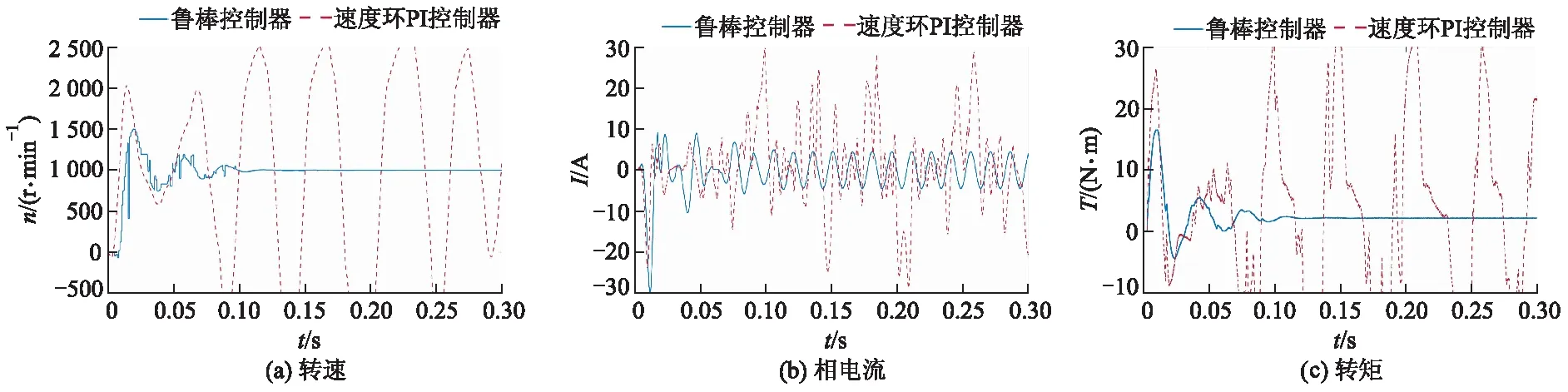
图8 非理想网络环境下电机转速、转矩和相电流对比曲线

4 结 论

文中构建了网络环境下永磁同步电机时滞动力学模型，基于模型设计了调速系统鲁棒控制器.利用SimEvents搭建控制器局域网络通信模块，并在MATLAB/Simulink中建立了仿真模型，对文中提出的控制策略进行了验证，得到如下结论:

1) 采用传统PI控制器的矢量控制方法无法满足非理想网络环境下永磁同步电机调速控制稳定性要求.

2) 通过构造Lyapunov-Krasovskii函数，可以得到网络环境下永磁同步电机调速控制系统稳定性条件.

3) 文中设计的调速鲁棒控制器，能够有效降低通信时滞对控制系统稳定性造成的影响，避免系统失稳的情况发生.