叶片挥舞振动后风轮流场特性
2020-05-13方玉财高志鹰闫萌萌陈永艳
方玉财, 高志鹰,闫萌萌, 陈永艳
(1. 内蒙古工业大学能源与动力工程学院,内蒙古 呼和浩特 010051; 2. 风能太阳能利用技术教育部重点实验室,内蒙古 呼和浩特 010051)
风力机作为转换风能为电能的旋转机械,工作运行条件极其复杂多变,其运行过程中不可避免地产生振动[1-3].而随着人类对风能资源开发利用程度的加深,风力机逐渐大型化,叶片也更长更柔,在运行过程中多变的外力和叶片弹性变形相互激励,使叶片振动变形加剧[4-5].这种振动会使叶片偏离设计点,对风轮流场特性产生较大的影响.而风轮流动特性是判定风力机优劣的方法之一[6-7].丁勤卫等[8]模拟研究了风力机结构动态响应叶片振动特性,得出挥舞振动为振动能量的主要部分.GONZALEZ等[9]、BARLAS等[10]研究了二维翼型扑翼运动气动力变化情况,但并未对三维振动风轮进行研究.朱由锋等[11]分析了弯振与摆振耦合情况下叶片气动力变化,得出弯振为主要影响因素,但并未对流场特性进行详细介绍.张俊红等[12]、岳萍等[13]研究了流固耦合作用下叶片振动特性.结合以上研究,文中主要进行风力机在三维运动状态下叶片挥舞振动后流场特性的非定常研究.
1 计算模型
1.1 大涡模拟
水平轴风力机在三维旋转过程中可以看作一个低速流体流动的过程.将空气假设为不可压缩流体.对能量守恒研究时主要考虑质量守恒与动量守恒.文中为了得出更加精确的计算结果,在进行三维旋转风轮非稳态计算时湍流模型选择大涡模拟,其主要利用Smagorinsky-Lilly模型进行计算,对不可压缩N-S方程进行求解.得出公式
(1)
(2)
式中:τij为亚格子应力.
1.2 叶片振型
通过在叶片表面布置若干对加速度传感器,利用力锤进行单点激励,多点响应方法,得出叶片的挥舞振型.通过模态试验得出:挥舞振动的能量主要集中在低阶振动上,因此,文中通过考虑施加低阶挥舞振动进行研究.图1为通过模态试验所得出的叶片在一阶振动及二阶振动的效果示意图.
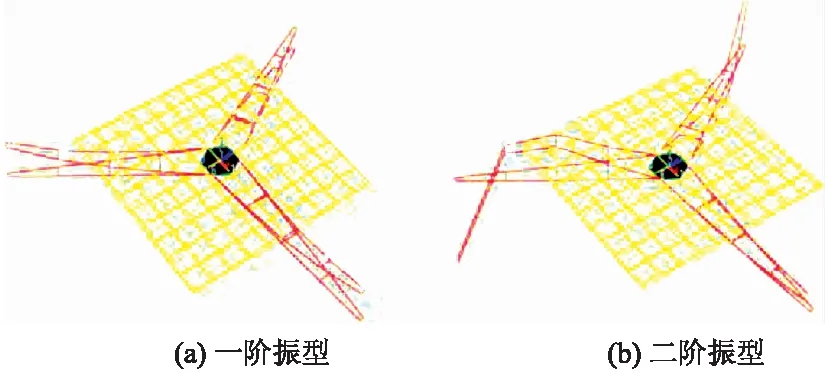
图1 叶片振型图
2 数值模拟
2.1 模型建立及网格划分
建立如图2a所示的计算域.计算域分为3部分:从里至外依次为旋转域、加密区、静止域.在旋转域与静止域间添加加密区,目的是使网格尺寸更好地过渡,以保证网格质量.数值模拟中既需要考虑风轮附近流场的精确性又需要优化计算速度.经多次验证,当计算域进口离风轮2D.出口5D(D为风轮直径)时可以保证计算速度与精度,尾迹后方不会出现回流,满足计算要求.在Mesh中利用体网格加面网格的方法可以优化网格质量.经过网格无关性验证,当网格总数约为380万时,网格质量符合计算要求,如图2b所示.
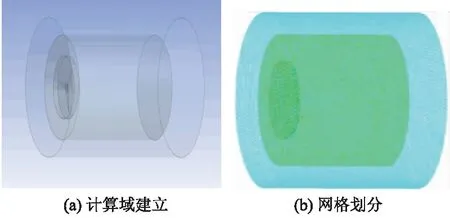
图2 模型建立及网格划分
2.2 边界条件
由于来流通过风轮后,其尾迹压力与速度在未计算时处于未知量,因而出口设置为自由流作为边界条件.入口设置成来流风速.
静止域与旋转域之间通过设置Interface1,2面进行数据传递.风轮包络面设置为Moving wall,运用动网格技术进行叶片振动的控制.旋转域采用滑移网格(moving mesh),模拟风轮的旋转,采用无反射边界(non-reflecting boundary)进行计算.
3 结果分析
3.1 速度场分析
为了探索施加低阶挥舞振动对风轮尾迹速度场的影响,在风力机额定工况(λ=5、v=8 m/s)时,截取风轮1个旋转周期内,不同时刻下速度云图,如图3所示.
从图3中可以看出,施加低阶挥舞振动后风轮尾迹速度场整体流动变得更加复杂,速度变化强度较明显.分析尾迹中心亏损区域可以发现,在相同瞬态时刻下非振动风轮尾迹中心区域和叶片中部附近速度亏损严重,而施加振动后风轮尾迹中心区域速度亏损程度相对减小,叶片中部附近并未发现明显亏损,叠加振动相对于一阶挥舞尾迹中心速度亏损程度更小,下1/4 周期内风轮在3种运动状态下的尾迹中心速度亏损程度与上一周期基本一致.
其次,通过分析叶尖亏损区域可以发现:相同瞬态时刻非振动条件下叶尖位置速度亏损较小,施加一阶挥舞振动后叶尖位置亏损明显,且在上游与下游亏损程度存在较大差异,上游亏损较为严重,而施加叠加振动后叶尖位置同样出现亏损,但上游与下游亏损程度接近一致.施加振动后叶尖处速度亏损较大的原因是施加振动后,叶尖位置处振动变形量相对较大,流体通过风轮叶尖位置流体绕流变得更强.

图3 风轮尾迹轴向速度云图
施加振动后叶尖涡诱导效应引起的速度增益区相对于未施加振动较大,且由未振动情况可明显看出单个叶尖涡引起的局部速度增大;施加振动后在接下来1/4周期内均发现叶尖涡效应区径向膨胀,且叠加振动膨胀趋势更为明显.
选取某一相同时刻,分析不同轴向位置处沿径向的速度分布情况,如图4所示.
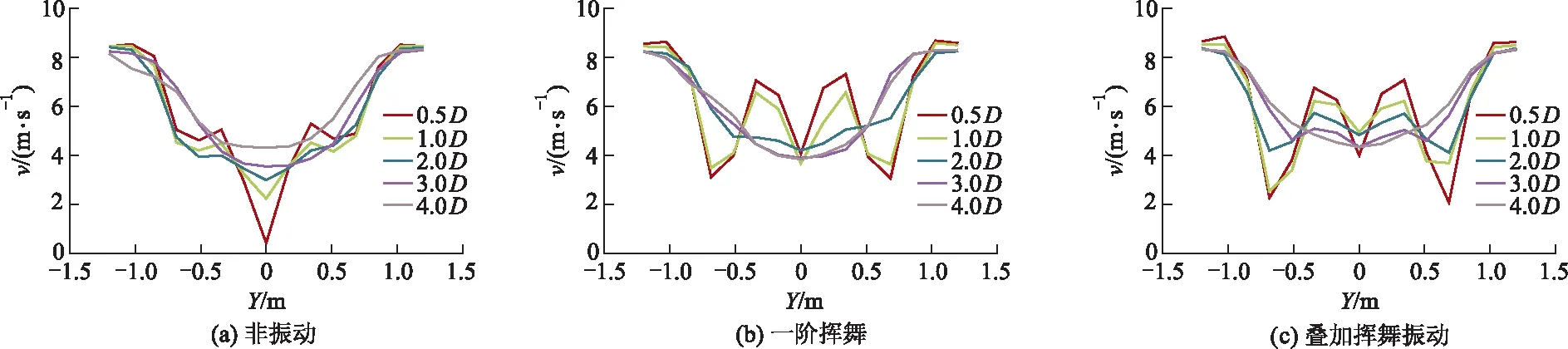
图4 振动前后不同轴向位置速度分布
文中定义某一区域内速度相对于非振动而言有较大幅度的提升,但此时速度并未超过来流速度,该区域称为“相对速度增益区”.由图4b可以看出,施加一阶挥舞振动后,轴向0.5D,1.0D处在叶中附近产生“相对速度增益区”;而施加一、二阶叠加振动后,在轴向0.5D,1.0D,2.0D,3.0D处,径向在叶中附近均出现“相对速度增益区”.
比较一阶振动与叠加振动可知:施加叠加振动后的“相对速度增益区”距离较一阶挥舞振动有所增加.原因在于一、二阶叠加振动比一阶挥舞振动的振动强度更大,因而对风轮尾迹速度影响更远.通过下节对风轮振动前后涡量场分析可知:“相对速度增益区”的产生是由于施加振动后风轮表面附着涡增加的缘故.
其次,叶片施加振动后,由于在叶片中部位置产生了“相对速度增益区”,而叶尖部位出现速度亏损区,因而,较非振动而言,施加振动后叶片上将形成较大的速度差,而较大的速度差会使得整只叶片受力更加不均匀,出现较大的压差.以上因素导致施加振动后会对风力机叶片结构产生较大危害,加速叶片的损坏与断裂.
3.2 涡量场分析
图5为施加振动前后风轮尾迹涡量Ω云图.从图5a中可以清晰发现:未施加振动时叶片在叶尖处产生较强的叶尖涡,且叶尖涡形成后,随着风轮的旋转,叶尖涡逐渐往下游脱落,且脱落运动轨迹明显.而施加振动后,在叶尖部分涡量较非振动时强度增强,且叶尖涡形成掺混,叶尖处涡的脱落较非振动时有延迟.这主要是因为施加振动后叶片在叶尖处变形量最大,来流经过叶尖位置时形成的扰流较大.其次,由于振动会影响叶片的气流分离,因而,施加振动后风轮表面附着涡强于非振动,这与云图规律相一致.同时下一个1/4周期内风轮在3种运动状态下的尾迹涡量场分布规律与上一周期基本一致.
为了定量研究风轮在不同运动状态下,风轮尾迹后方的涡量耗散分布规律,选取不同轴向位置处涡量分布的变化情况进行分析.图6为风轮在3种运动状态下涡量耗散分布情况.

图5 振动前后风轮尾迹涡量图
Fig.5 Vorticity diagram of wind wheel wake before and after vibration
由图6a可以看出,非振动时涡量沿尾迹中心呈现对称分布趋势,且在尾迹中心与叶尖涡影响区域分别出现涡量峰值.从图6b,6c可以看出,施加振动后涡量分布与非振动相比更加复杂,尤其是靠近风轮附近处.施加振动与非振动相比,施加振动后在轴向0.5D,1.0D位置处涡量沿尾迹中心呈非对称分布,且在叶尖涡附近处耗散速率逐渐增大.其次,无论是振动还是非振动,随着轴向距离的增加,整体涡量值均逐渐减小.
3.3 脉动压力分析
图7,8,9分别为风轮在非振动、一阶振动、一二阶叠加振动3种运动状态下不同径向位置s压力脉动变化规律.时域图为 1.10~1.35 s风轮2个旋转周期内压力脉动p的变化情况,从图可以发现:非振动与施加振动后在0.3,0.5,0.7 m 3个监测点处的压力脉动均呈现周期性波动.径向0.5 m监测点的压力脉动波动最为明显,叶尖0.7 m监测点的压力脉动波动范围次之,0.3 m波动最小.比较振动与非振动情况:施加振动后相同监测点的压力脉动与非振动相比有明显提升,波动范围更加明显.
Fig.7 Pressure pulsation at different radial positions when non-vibrating

图8 一阶振动时不同径向位置处压力脉动
Fig.8 Pressure pulsation at different radial positions during first-order vibration
对图9a中数据进行FFT变化后得到图9b所示的压力脉动频谱图.从频谱图中可以看出,各监测点压力脉动的频率主要集中于基频及其倍频上.其次,在相同监测点0.5 m位置处风轮在非振动基频处的通过幅值A为14.67,在一阶振动及叠加振动分别为21.32,19.15,较非振动分别增长了6.65,4.48.由此可见:施加振动后监测点幅值明显大于非振动时.
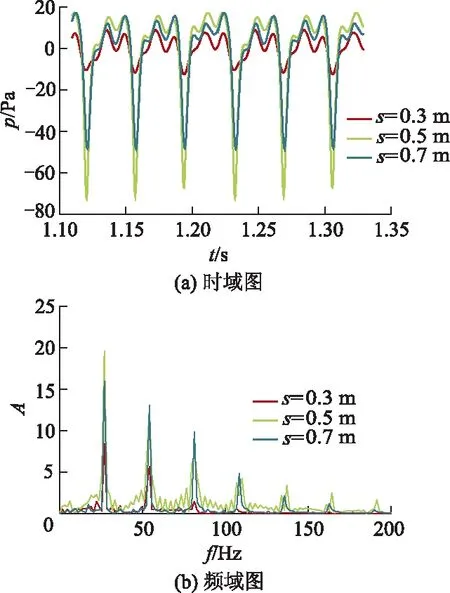
图9 叠加振动时不同径向位置处压力脉动
Fig.9 Pressure pulsation at different radial positions when superimposing vibration
4 结 论
运用ANSYS仿真软件对风轮非振动、施加一阶振动及一二阶叠加挥舞振动后近尾迹流场特性进行研究.文中得出以下结论:
1) 引入了“相对速度增益区”的概念,得出叶片施加挥舞振动后,叶片中部位置产生了“相对速度增益区”,而叶尖部位出现速度亏损区,这也揭示了施加振动后叶片将更易出现折断等危害.同时,施加振动后在1个旋转周期内均发现:叶尖涡效应区会产生径向膨胀,且叠加振动膨胀趋势更为明显.
2) 非振动时涡量沿尾迹中心近似呈对称分布趋势,且在尾迹中心与叶尖涡影响区域出现涡量峰值.0.5D,1.0D轴向位置处涡量沿尾迹中心呈现非对称分布,且施加振动后叶尖涡附近处涡量耗散速率逐渐增大.
3) 压力脉动均呈现周期性波动.径向0.5 m监测点的压力脉动波动最为明显,各监测点脉动压力主要频率集中基频及其倍频.
