回归模型在Meta分析中的应用及Stata实现
2020-05-13周晓慧尤爱军李娅欣范竹萍范慧敏
周晓慧,尤爱军,李娅欣,范竹萍,范慧敏,郑 亮
(1.同济大学附属东方医院上海市心衰研究所,上海 200120;2.同济大学医学院预防医学系,上海 200092;3.上海交通大学医学院附属仁济医院消化科,上海 200120)
循证医学(evidence⁃based medicine)是系统地检索、评价和应用现有最新研究成果的医学方法,并以此作为临床决策的依据。它是遵循证据的医疗决策,服务于临床指南以及医疗卫生政策的制定[1⁃3]。Meta 分析(又称荟萃分析)是一种可以将多个具有同质性研究结果的研究进行系统的、定量地综合合并的研究方法[4]。它是一项可定量的合并研究,也是循证医学领域中一个重要组成部分,因此要遵循循证科学研究的一般设计原理。其过程包括确立研究目的、收集数据、统计分析以及做出最终的结论。其中回归模型的使用是Meta 分析中一种重要的统计方法[5],它可以用于分析异质性过大的原因,进而发现与筛检异质性的来源;也可以用于预测因变量与自变量的变化关系。下面本研究将从这两个方面来介绍一下Meta 回归在循证医学中的应用与Stata 软件的实现步骤。
1 资料与方法
本研究所采用的数据均来自于已经发表的文章数据,1 篇为 Zheng 等[2]在Eur J Clin Nutr上的一篇Meta 分析的原始数据;另 1 篇为 Hourcade⁃Potelleret等[6]在Heart上的1 篇文章的原始数据,具体数据详见表1~2。
Meta 分析可以使用多种软件加以实现,最常用的专业软件包括 SAS、R、Stata、Revman、Metadisc等。其中 Stata 是一种较为成熟的商业软件,在Meta 分析过程中可以采用菜单式操作或者是编写程序来加以实现,可以完成数据的手动录入、管理分析、图形制作、结果输出等功能。其在网络Meta 分析和剂量反应Meta 分析中显示出了强大的功能与兼容优势。
Meta 回归分析的统计模型是固定效应模型,模型假定各项研究的效应大小的影响因素是相同的。但在大量的现实研究中,绝大多数问题是使用随机效应的回归模型的,因此本文就随机效应模型数学原理进行简单介绍[7⁃8]。其对应的随机效应回归模型数学公式为如下。
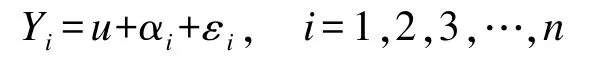
这里αi表示随机效应,并且满足E(αi)=0;αi与εi是相互独立的。
通常,Meta 回归方法侧重于通过建立线性或非线性回归方程来发现异质性的原因、进行风险因素预测等。一方面,Meta 分析本身的特点决定了异质性的处理是这种方法是否应用得当的一个关键之处,换言之如果异质性过大就代表了所纳入文献合并效应的计算过于牵强,有必要分析是什么导致了该异质性过大;另一方面,线性或非线性回归方程就是评估当X 变化时,会引起Y 发生什么样的变化,利用这一特点就可以实现所要的预测目的。下面就通过具体实例来加以举例说明,使用的软件为Stata 14.0(Stata Corp LP,USA)。
2 举例说明
2.1 筛检异质性的来源
以 2015年 Zheng 等[2]在Eur J Clin Nutr上的一篇Meta 分析的原始数据为例,说明通过构建Meta 回归模型来筛检出导致研究异质性较高的因素,并且通过亚组分析来降低其异质性。这里纳入原始研究均为随机对照研究,合计12 篇,基本数据结构情况请见表1。
Stata 实现步骤如下。(1) 打开研究所整理好的数据集;(2) 在 Stata 菜单栏中点击 user/Meta analysis/regression(Metareg) 菜单;(3) Metareg 中勾选因变量和自变量;(4) 勾选OK 即可得到如下结果,当然也可以直接输入图1 中的Stata 程序,进而得到完全相同的结果。
根据这一回归结果可以得出结论:纳入文章的设计分型、以及研究开展地域都不是导致本次异质性过大的影响因素;再尝试不同的因素组合情况,直至把有意义的影响因素找到为止,然后按照所找出的因素或者变量来进行进一步的亚组分析,得到具有亚组效应的和总体效应的森林图。
2.2 预测因变量与自变量的变化关系
以 Hourcade⁃Potelleret 等[6]在Heart上的 1 篇文章的原始数据为例(表2)说明如何构建Meta 回归模型来评估高密度脂蛋白( high density lipoprotein,HDL)的改变与效应量RR 值的对数值之间的变化关系,进而推断每当HDL 改变1 个基本单位时,logRR 值对应的改变数量,共有8 篇研究文章符合纳入标准。
由表2 和图2 可以看出,当以HDL 为自变量X而以logRR 作为因变量Y 时,可以建立一元一次方程Y=1.06-0.188X。由于 RR 值是一种率比呈偏态分布,因此对RR 取对数即logRR 作为因变量Y。回归过程的结果如图2 所示,X 的系数为-0.188,该结果与原文中结果是一致的。作者利用了构建方程来达到体现在叶酸组中HDL 的改变量与效应量对数值之间的变化关系,即可以用HDL 的变化来预测效应量。
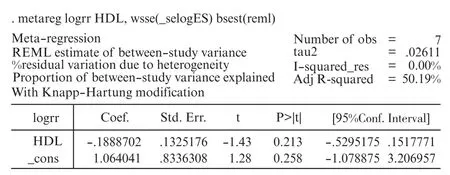
图2 使用Meta 回归探讨HDL 的改变量与logRR 之间的变化关系Fig.2 The relationship between changes in HDL and logRR with Meta⁃regression
当想看RR 的原值时,可以勾选eform 反对数选项,即可把系数Coef 转变为EXP 及RR 值。由图3可以看出,除了RR 值完成了转换,而其他各个参数均与图2 一致,并没有发生任何改变。
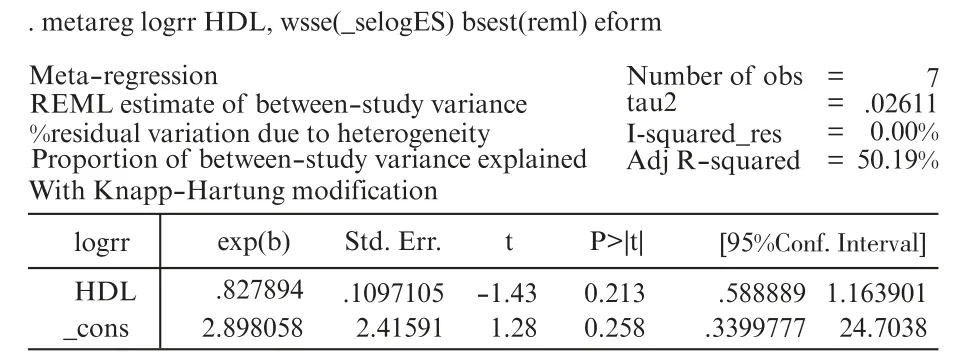
图3 用Meta 回归探讨HDL 的改变量与logRR 之间的变化关系Fig.3 The relationship between changes in HDL and logRR with Meta⁃regression
2.3 其他应用
Meta 回归的用法还有很多种情况,如在剂量反应Meta 分析中的回归模型应用也是一种常见的情况,无论是单一研究的剂量反应Meta 分析,还是多个研究合并的剂量反应Meta 分析,回归模型都是呈现所研究的摄入剂量和终点事件的反应(效应)的线性或非线性变化关系,对于以上临床科研中的实践问题,读者可以根据自己碰到的实际情况来加以选用。
3 讨 论
本质上Meta 回归分析是利用了回归模型来解决自变量与结局变量之间相关性的问题,例如通过分析高危因素导致了疾病的高发来寻找异质性来源,或者通过一元一次或多元一次方程的系数预测因变量与自变量的变化关系。
本研究的例题1 清晰地显示出,在所关心的影响因素中,研究地域的差异很可能是引起异质性较大的原因。正是通过该因素进行了亚组分析后,有效地降低的I2值。一开始入选研究总体I2为94.5%,经过亚组分析后,两个亚组对应的I2分别为93.7%与 81.6%[2]。以上方法也是 Meta 分析中的有效手段[9]。
在Meta 回归中,预测因变量与自变量的变化关系也是常见的解决临床问题的工具。本研究的例题2显示,当研究所关注的是单一因素的模型中剂量变化关系时,HDL 每一个单位的增加会导致logRR 值发生0.188 个单位的下降[6]。正是利用了回归方程到达了文章所关注的研究目的。Meta 分析的许多领域都是和Meta 回归有着密切的联系,例如剂量反应的 Meta 分析[10⁃11]等等。
虽然本研究通过已经公开发表文章的实例说明了Meta 回归分析在循证医学研究中的常见用途,但也存在一些不足。首先,在探讨导致异质性过高的分析中,当存在多个影响因素之间的交互作用时,Meta 回归分析后的亚组分析可能无法达到降低I2的效果[12];其次,Meta 回归本质上是一种理论化的数学模型,对于临床实践中的混杂因素效果并不理想。再次,本文仅对Meta 回归几种常见的用途进行了描述与示范,需要更多进一步的研究来详解Meta回归的其他用途,从而使研究者能更好地使用这一方法解决实际临床问题。
