超空泡航行器尾部滑行流场特性数值仿真与试验

张 珂, 孙士明, 颜 开, 王 志, 李 鹏

超空泡航行器尾部滑行流场特性数值仿真与试验

张 珂, 孙士明, 颜 开, 王 志, 李 鹏1

(中国船舶科学研究中心 水动力学重点实验室, 江苏 无锡, 214082)

超空泡航行器尾部滑行升力对运动姿态具有重要影响。文中基于流体体积(VOF)多相流模型, 开展了不同后体攻角下超空泡航行器尾部在空泡内滑行过程的数值仿真, 通过与试验数据对比验证了数值仿真的有效性, 并在此基础上分析了空泡形态及尾部流场压力的变化规律。研究结果表明: 空泡在沾湿面附近由于压差作用会向航行器表面卷曲, 并引起向上的飞溅流动, 沾湿面压力沿空泡轮廓线方向的衰减速度比沿航行器下缘的衰减速度更快。研究结果可为滑行力建模提供参考。

超空泡航行器; 尾部; 滑行升力; 数值仿真; 流场特性

0 引言

超空泡航行器在运动过程中被超空泡包覆, 其尾部稳定浸入水中滑行和尾部周期性拍击空泡壁面是保持运动基本稳定的2种常见模式[1]。航行器尾部在空泡中沾湿滑行过程的流体动力特性对其运动姿态具有重要影响。滑行升力量值与尾部沾湿面状态密切相关, 且尾部沾湿部分高压会影响空泡形态, 引起空泡的局部变形, 因此研究超空泡航行器尾部滑行流场特性具有重要意义。

超空泡航行器尾部滑行力的研究始于Waid等[1]的试验工作, 其后Logvinovich[2]、Rand[3]、Kulkarni[4]以及Paryshev[5]通过理论研究建立了不同的滑行力模型。Yen[6]和Dzielski等[7]在拖曳水池中研究了圆柱体在水平自由面和空泡中的滑行水动力特性; Moroz[8]和Serebryakov等[9]通过试验和理论研究分析了圆柱体与空泡的相互作用。数值仿真方面, 李其弢[10]研究了纵摆过程中的超空泡航行器流体动力; 于开平等[11]建立了三维超空泡航行器动力学仿真模型, 对超空泡航行器巡航状态动力学行为进行了数值仿真; 周景军等[12-13]通过圆柱体模型和不同攻角下超空泡航行器的数值仿真, 研究了其尾部流体动力特性。目前, 超空泡航行器尾部动力特性的计算通常通过对比空泡形态或航行器整体力等间接方式进行验证, 而对航行器尾部滑行力测量试验与对比计算则研究较少。

文中基于流体体积(volume of fluid, VOF)多相流模型, 开展了超空泡航行器圆柱后体在不同攻角下滑行过程的数值仿真, 并通过尾部滑行力流体动力测量试验数据对比进行了验证, 在此基础上分析了空泡形态和压力等流场特性的变化规律。

1 数值仿真方法

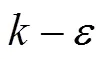
VOF多相流模型中所有流体满足同一组动量方程, 在整个计算区域上跟踪每种流体在每个计算单元的体积分数。连续方程和动量方程分别为

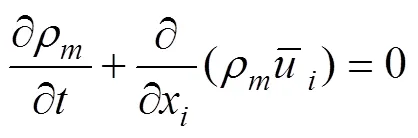
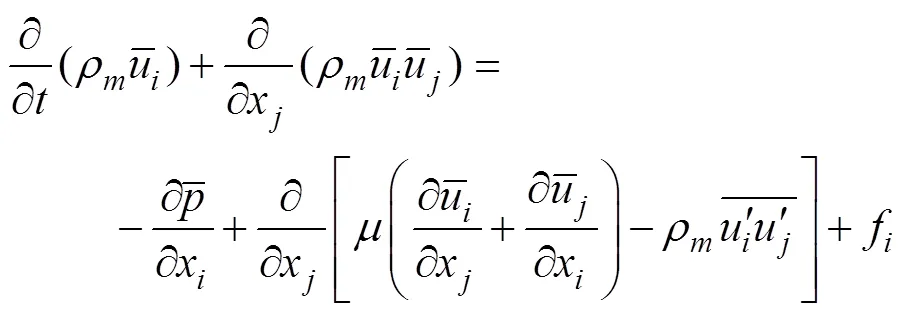
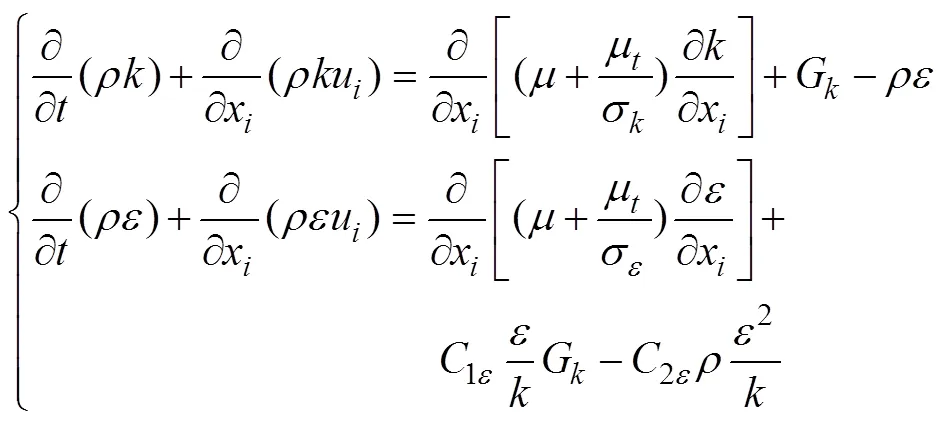
计算中应用了重叠网格方法对流场进行划分。重叠网格方法是一种区域分割与网格组合的策略, 涉及到背景网格和嵌入其内的重叠网格2种网格, 经过挖洞等预处理过程建立不同区域流场变量在网格重叠或嵌套区域边界上的传递关系, 流场信息在重叠区域通过插值方法进行交换和耦合, 最终实现流场域的整体计算。

2 计算模型与网格

计算模型的长度和直径等参数与水洞试验模型一致, 计算域与边界条件如图1所示。来流采用速度入口边界, 出口方向采用压力边界, 侧面采用壁面边界, 忽略了支柱的影响, 计算模型和计算域选取整个区域的一半, 计算域的高度和宽度分别为225 mm和112.5 mm, 计算域入口与模型前端距离约为模型长度的1.8倍, 计算域出口距模型后端约为模型长度的3.6倍。计算模型直径为40 mm, 总长度为390 mm, 空化器直径45 mm。计算采用重叠网格方案, 模型后段为重叠网格区域, 通过重叠区域的转动实现尾部不同的攻角姿态, 网格在模型附近及尾流区域进行了局部加密, 模型表面网格如图1所示, 总体网格量约为2.7×106。

3 滑行力水洞测量试验

圆柱后体滑行流体动力测量试验在中国船舶科学研究中心多功能高速空泡水洞开展。该水洞为立式循环水洞, 工作段截面为225 mm × 225 mm的正方形, 长度为1.5 m。其主要性能技术指标为: 水速0~25 m/s连续可调, 压力范围10~500 kPa。试验获得了不同圆柱后体静态攻角下的滑行面几何特征及尾部沾湿滑行力特性。

试验模型为中间断开的前后两段, 采用腹支撑的方式安装在水洞侧壁, 如图2所示。模型前段通过支撑键固定在水洞内壁, 模型后段为可以绕转轴摆动的圆柱后体, 其摆动角度通过外置电机加以控制, 测量滑行力的应变式天平一端通过支撑杆与圆柱后体连接, 另一端通过减速机主轴与控制电机相连。

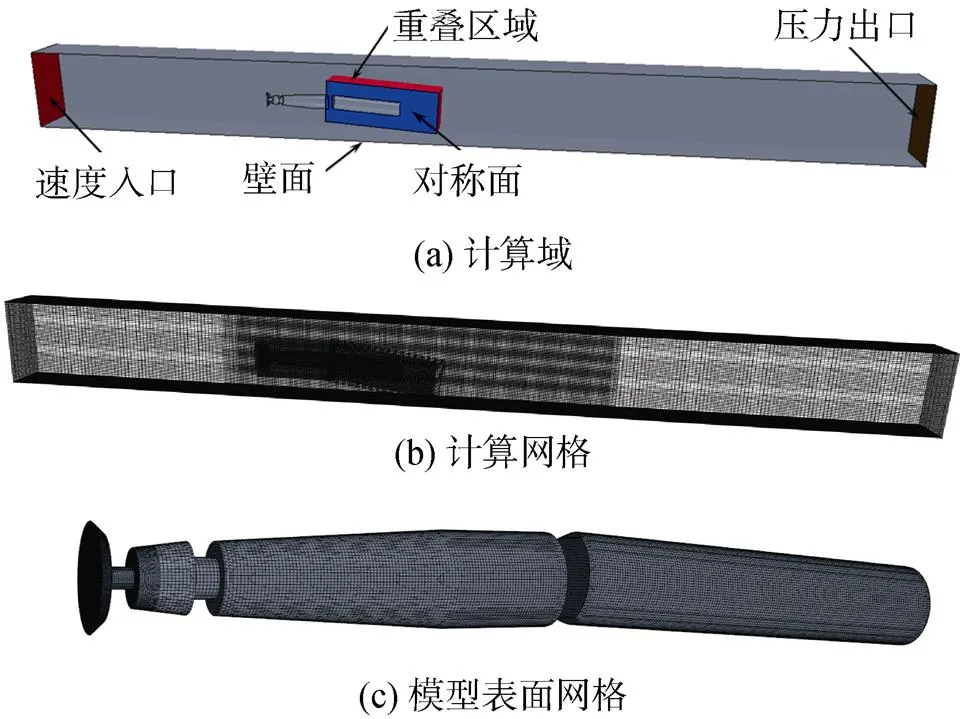
图1 计算域与计算网格示意图

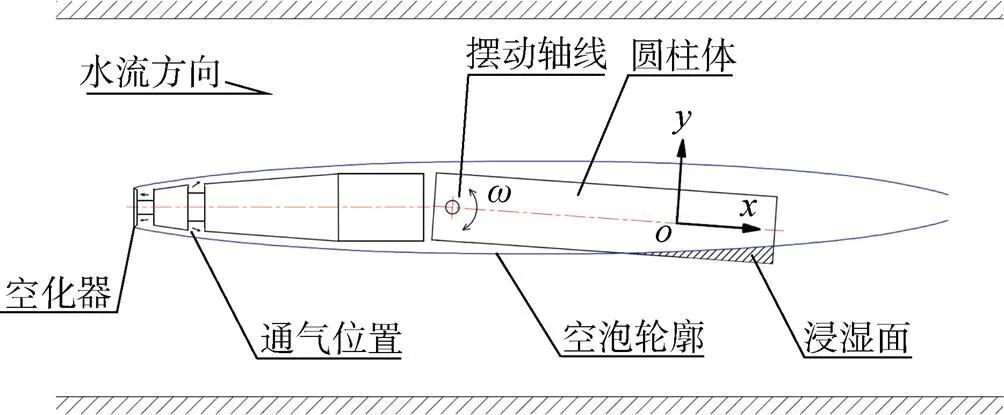
图2 滑行力测量试验示意图

4 数值仿真结果与分析

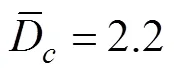
1) 空泡形态

图4为模型后体不同攻角下空泡形态数值仿真结果, 为与试验结果比较, 图5给出了数值仿真尾部沾湿面状态。当模型后体局部浸没沾湿, 空泡在沾湿面附近会发生局部变形, 使得空泡局部轻微向上凸起, 并向内卷曲, 有较薄的液层在模型表面形成向上的飞溅流动(见图5), 与试验中的飞溅流动区域(见图3)对比可知, 模型后体攻角越大, 飞溅流动影响区域越大。在模型后体沾湿面末端, 由于流动分离而形成空泡, 并与主体超空泡连通。数值仿真滑行沾湿面以及空泡形态局部变化特性与试验规律一致。

图3 不同攻角下模型后体试验照片

图4 不同攻角下模型后体空泡形态

2) 滑行升力

图6为数值仿真和试验获得的升力系数C的对比曲线。可见数值仿真滑行升力系数变化趋势与试验结果一致, 量值较试验结果略微偏大, 验证了数值仿真方法的有效性。假设滑行浸没角与攻角近似相等, 则滑行升力随浸没角近似呈线性关系。

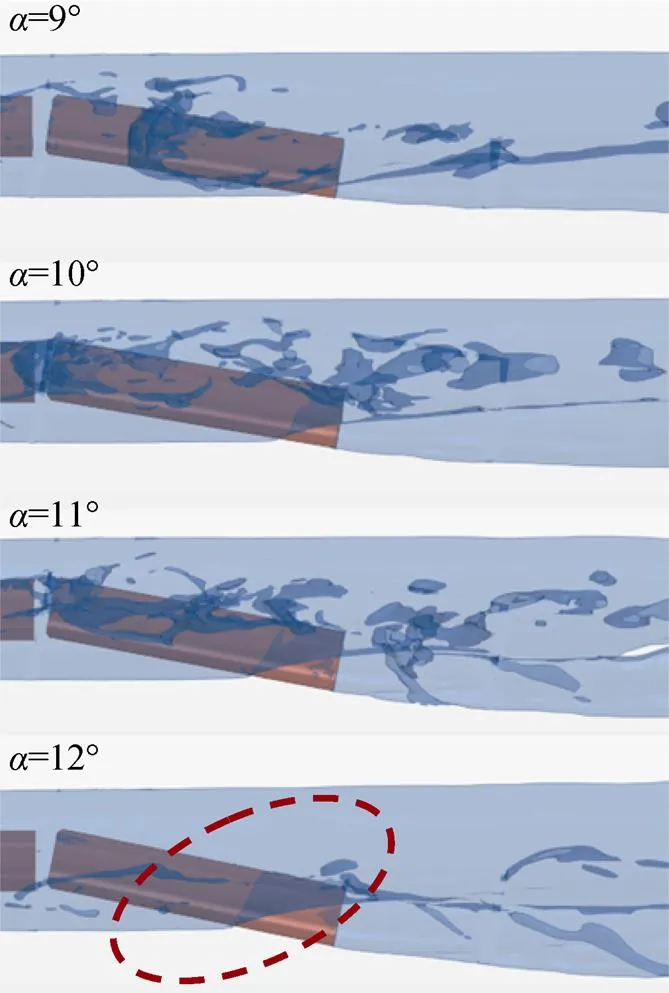
图5 模型后体沾湿滑行面数值仿真结果

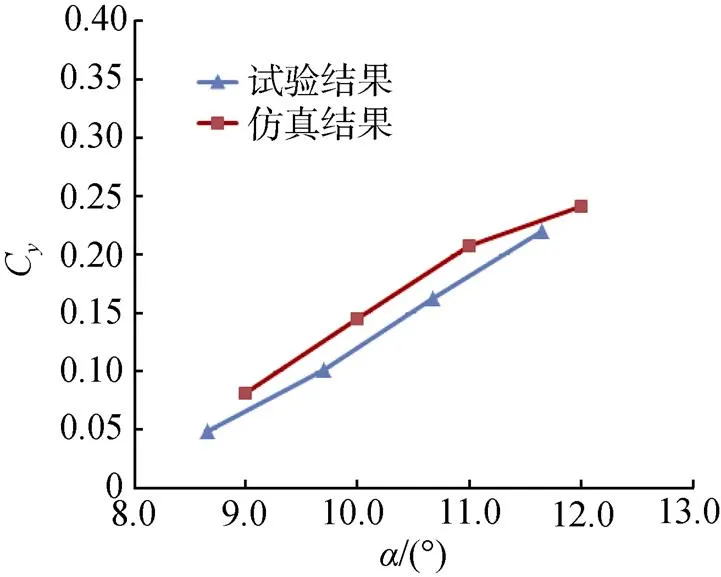
图6 数值仿真和试验升力系数对比

3) 尾部压力场特性

图7为模型尾部压力系数分布等值线图。从图中可以看出, 当模型尾部产生浸没时, 空泡轮廓与模型相交位置驻点压力最高, 随后沿轴线方向迅速衰减。从压力系数分布上看, 压力沿空泡轮廓线方向的衰减速度比沿模型下缘衰减速度更快, 原因是空泡形态在浸没区域发生了局部变形, 空泡内卷形成液层的飞溅流动, 造成了空泡轮廓线附近动量的损失。这种趋势在攻角越大时更加明显, 对应飞溅流动的区域也越大。而驻点高压对泡内压力影响不大。

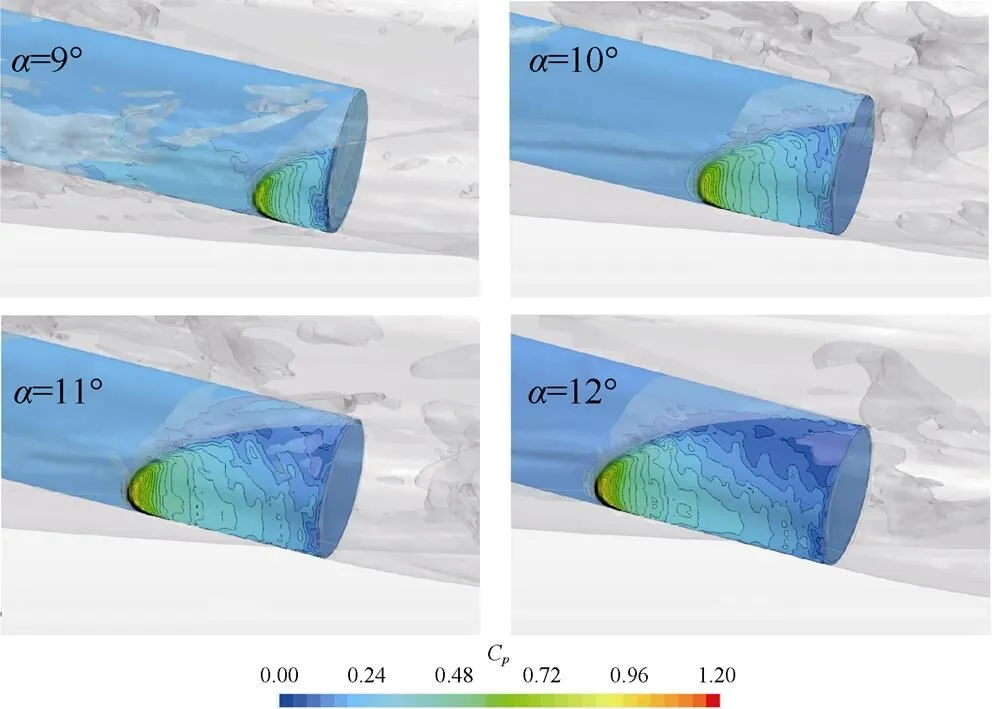
图7 模型尾部及对称面压力系数分布等值线图

图8为模型下缘沿轴线方向压力系数C分布。从图中可以看出, 模型圆柱后体的攻角对压力分布具有明显影响, 攻角越大, 沾湿区域压力峰值越高, 但压力峰值并不与圆柱后体攻角呈线性变化的趋势。不同攻角下, 在模型下缘末端的压力较为接近, 均低于浸没区域前的泡内压力。

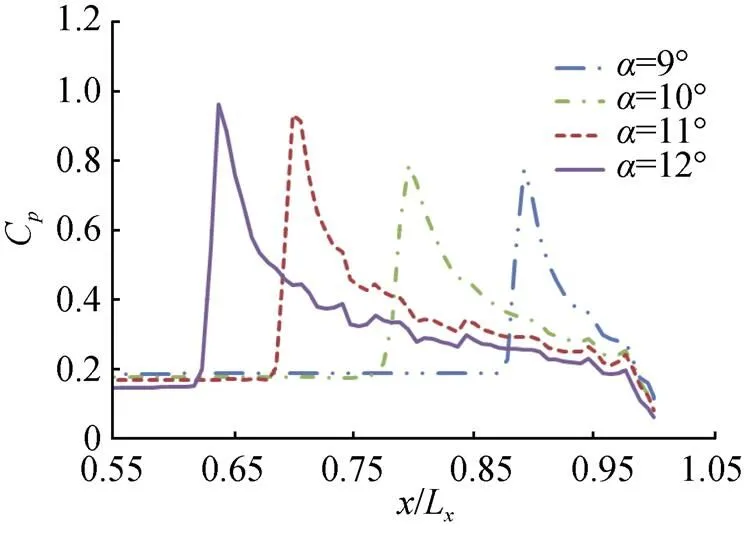
图8 模型下缘沿轴线方向压力系数分布曲线

4) 尾部空泡流场速度分布

图9为模型后体攻角=12°时, 尾部的空泡壁面流线图, 可见空泡内卷后液层流动方向在前段趋于垂直向上, 在后段趋向空泡轮廓。

图10为浸没部分等距离截面示意图, 图11为各截面速度矢量图, 其中黑色实线为截面空泡轮廓。可见在截面1空泡下表面根部形成了向上流动的液层, 空泡根部变形较小。随着飞溅液层的发展, 从截面1至3空泡根部变形逐渐增大, 液层的垂向速度逐渐减小, 这是由于来流方向沾湿面压力逐渐衰减, 即沾湿面与泡内压差沿来流方向减小导致。

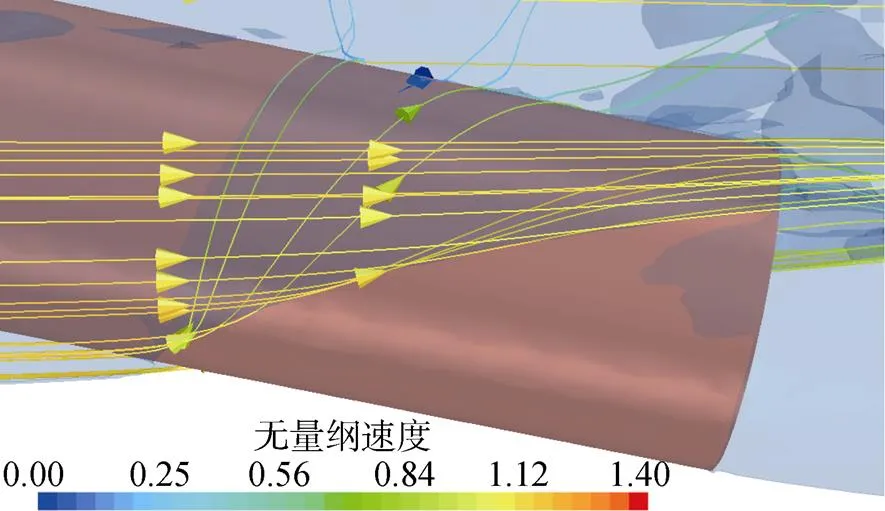
图9 尾部流线图

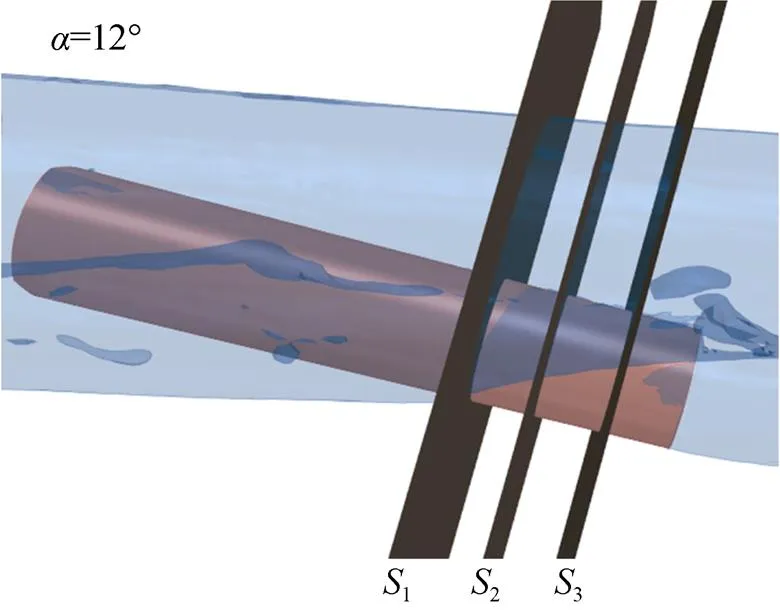
图10 等距离截面示意图

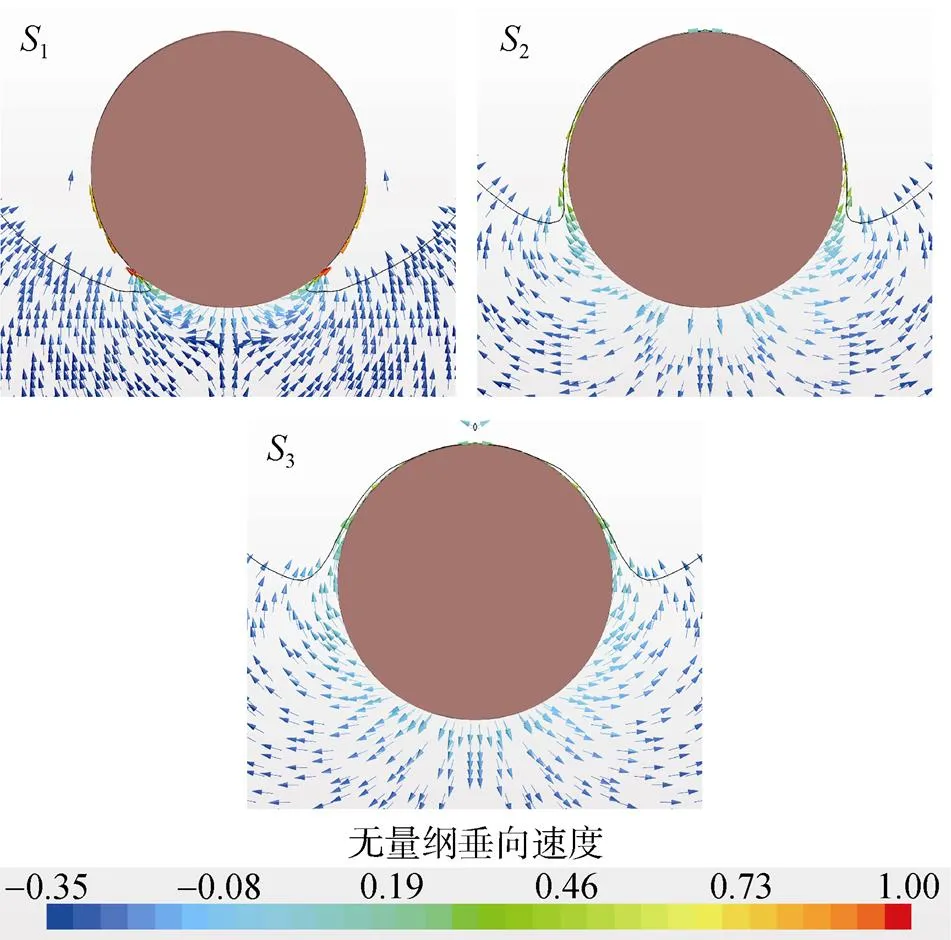
图11 不同截面垂向速度等值线图

5 结论

文中开展了超空泡航行器圆柱后体不同攻角下尾部滑行的数值仿真研究, 并通过尾部滑行力试验数据对比进行了验证, 在此基础上获得了模型尾部空泡形态、压力场及速度场的变化规律, 获得如下结论:

1) 由于沾湿面压力高于泡内压力, 空泡在沾湿面附近会发生局部变形, 并向内卷曲, 有液层在模型表面形成向上的飞溅流动;

2) 空泡轮廓与模型相交位置驻点压力最高, 随后沿轴线方向迅速衰减。压力沿空泡轮廓线方向的衰减速度比沿模型下缘衰减速度更快, 模型后体的攻角对压力分布具有明显影响, 攻角越大, 沾湿区域压力峰值越高;

3) 空泡内卷后, 液层流动方向在前段趋于垂直向上, 在后段趋向空泡轮廓, 液层的垂向速度沿来流方向逐渐变小。

文中研究结论可为滑行升力建模提供参考。

[1] Waid R, Kermeen R. Forces on Cylinders Planning on Flat and Curved Surfaces in Cavitating and Non-Cavitating Flow[R]. US: California Institute of Technology, 1957.

[2] Logvinovich G V. Hydrodynamics of flows with free boundaries[M]. Kyiv: Naukova dumka, 1969.

[3] Rand R, Pratap R, Ramani D, et a1. Impact Dynamics of a Supercavitating Underwater Projectile[C]//Proceeding of the 1997 ASME Design Engineering Technical Conferences. USA: Sacramento, California, 1997．

[4] Kulkarni S S, Pratap R. Studies on the Dynamics of a Supercavitating Projectile[J]. Applied Mathematical Mode- lling, 2000, 24(2): 113-129．

[5] Paryshev E V. Approximate Mathematical Models in High-Speed Hydrodynamics[J]. Journal of Engineering Mathematics, 2006, 55(1-4): 41-64.

[6] Yen T, Morabito M, Imas L, et al. Investigation of cylinder Planing on a Flat Free Surface[C]//Proceedings of 11th International Conference on Fast Sea Transportation, American Society of Naval Engineers. USA: Honolulu, Hawaii, 2011.

[7] Dzielski J E, Sammut P, Datla R. Planing-hull Forces and Moments on a Cylindrical Body in a Cavity[C]//Procee- dings of the 8th International Symposium on Cavitation. Singapore: National University of Singapore, 2012.

[8] Moroz V, Kochin V, Serebryakov V, et al. Experimental study of Planning Motion of a Cylinder Along the Nearly Axisymmetric Supercavity Surface[C]//Proceedings of the 10th International Symposium on Cavitation. USA: Johns Hopkins University, Baltimore, Maryland, 2018.

[9] Serebryakov V V, Moroz1 V V, Kochin1 V A, et al. Experimental Study on Planing Motion of a Cylinder at Angle of Attack in the Cavity Formed Behind an Axisymmetric Cavitator[C]//Proceedings of the 32nd Symposium on Naval Hydrodynamics. Germany: Office of Naval Research, Hamburg, 2018.

[10] 李其弢. 通气超空泡航行器水下摆动运动试验与模拟[D]. 上海: 上海交通大学, 2009.

[11] 于开平, 张广, 邹望, 等. 超空泡航行体纵向平面动力学行为的CFD 分析[J]. 船舶力学, 2014, 18(4): 370-376.Yu Kai-ping, Zhang Guang, Zou Wang, et al. CFD Analysis of the Dynamic Behavior of Supercavitating Vehicle in the Longitudinal Plane[J]. Journal of Ship Mechanics, 2014, 18(4): 370-376.

[12] 周景军, 于开平, 杨明. 基于均质多相流的超空泡航行体尾部升力数值模拟[J]. 水动力学研究与进展, 2010, 25(1): 113-118.Zhou Jing-jun, Yu Kai-ping, Yang Ming. Numerical Simulation on Lift of Aft Section of Supercavitating Bodies Based on Homogeneous Multiphase Model[J]. Journal of Hydrodynamics, 2010, 25(1): 113-118.

[13] 周景军, 赵京丽, 项庆睿. 超空泡航行体操纵过程流体动力特性数值模拟研究[J]. 船舶力学, 2018, 22(5): 560-568. Zhou Jing-jun, Zhao Jing-li, Xiang Qing-rui . Numerical Simulation on the Hydrodynamics of Supercavitating Vehicle in the Process of Steering[J]. Journal of Ship Mechanics, 2018,22(5):560-568.

Numerical Simulation and Experiment on Fluid Field Characteristic of Planing for Supercavity Vehicle Tail

ZHANG Ke, SUN Shi-ming, YAN Kai, WANG Zhi, LI Peng

(National Key Laboratory of Science and Technology on Hydrodynamics, China Ship Scientific Research Center, Wuxi 214082, China)

The planing lift acting on the tail of a supercavitating vehicle has an important influence on its underwater moving posture. In this paper, the volume of fluid (VOF) multiphase flow model was employed to numerically simulate the supercavitating vehicle’s tail planing in cavity at different attack angles. The numerical simulation was verified by comparison with the experimental data. Then, the deformation of the cavity and the variation of the pressure distribution were analyzed. Numerical simulation results showed that the cavity curled towards the vehicle surface near the wetted area with pressure gradient, which produced an upward splashing flow. The decay rate of the pressure along the cavity outline is larger than that along the bottom edge of the vehicle.

supercavity vehicle; tail; planing lift; numerical simulation; fluid field characteristic

O235; U661.1

A

2096-3920(2020)02-0126-07

10.11993/j.issn.2096-3920.2020.02.002

张珂, 孙士明, 颜开, 等. 超空泡航行器尾部滑行流场特性数值仿真与试验[J]. 水下无人系统学报, 2020, 28(1): 126-130.

2019-12-05;

2020-01-06.

张 珂(1984-), 男, 硕士, 高级工程师, 主要研究方向为空泡流理论及其应用技术.

(责任编辑: 陈 曦)