基于可观测度反馈的SINS/DVL组合导航算法

李志炜, 岳 崴, 高胜峰, 蔡 鹏, 朱海荣

基于可观测度反馈的SINS/DVL组合导航算法

李志炜1, 岳 崴2, 高胜峰2, 蔡 鹏2, 朱海荣2

(1. 中国人民解放军91001部队, 北京, 100080; 2. 海军潜艇学院, 山东 青岛, 266199)

针对捷联惯导/多普勒计程仪(SINS/DVL)组合导航中部分系统状态对无人水下航行器(UUV)导航精度影响较大但可观测性相对较弱的问题, 提出一种基于可观测度反馈的SINS/DVL组合导航算法。该算法通过量化分析系统各状态参数的可观测性, 根据系统状态参数在不同机动状态下可观测度不同的特点, 构造基于可观测度反馈的自适应调节因子, 增加高可观测度时的系统状态参数的估计占比, 以此来提高组合导航滤波算法的适应性和滤波估计精度。利用湖试数据对上述算法的性能进行了验证。结果表明, 可观测度反馈滤波算法累积误差明显小于常规卡尔曼滤波算法, 在相同的精度要求下, 可延长水下SINS/DVL组合导航自主航行的时间。

无人水下航行器; 组合导航; 捷联惯导; 多普勒计程仪; 可观测度

0 引言

无人水下航行器(unmanned undersea vehicle, UUV)因其目标特征小、隐蔽性好、工作范围广的优点已逐渐成为探测海洋、利用海洋的重要工具, 而实时准确的导航信息是UUV顺利执行任务的基础[1]。受体积和成本的限制, 目前UUV搭载的导航系统通常为捷联惯性导航系统(strapdown inertial navigation system, SINS)与多普勒计程仪(Doopler velocity log, DVL)等辅助导航设备组合的形式[2-3]。

目前提高SINS/DVL组合导航系统定位精度的方法主要有2种: 一是使用改进的滤波算法, 文献[4]利用滤波收敛判据对Sage-Husa自适应滤波器进行改进, 从而提高基于自适应滤波算法的SINS/DVL组合导航系统稳定性和导航精度; 文献[5]采用了球面最简相径采样规则改进容积卡尔曼滤波, 并通过数学平台仿真验证了该算法在S1N/DVL组合导航系统中的有效性。一是使用改进SINS/DVL的组合形式, 文献[6]推导了SINS/ DVL的紧组合导航形式, 并利用卡尔曼滤波信息进行故障检测与隔离, 有效提高了系统导航精度。但是这些方法都没有解决SINS/DVL组合导航系统中部分状态参数可观测性弱的问题, 并且具有在不同机动状态下可观测度不同的特点[7]。特别地, 惯性系统轴陀螺漂移的可观测性相对较弱, 这也是在初始对准中方位失准角通常收敛更慢的原因。而且相对水平陀螺漂移,轴陀螺漂移对SINS/DVL组合导航精度的影响更大。

可观测性分析的方法有很多, 应用于惯性导航可观测性研究中主要有分段线性定常系统(piecewise constant system, PWCS)方法[8]和非线性全局可观测性分析方法[9]。可观测性分析方法一般只能给出系统可观与不可观的结论, 而实际中往往更希望得到定量的分析结果, 文献[10]和文献[11]给出了基于可观测矩阵的奇异值或特征值来求解状态可观测度的方法; 文献[12]基于PWCS提出利用可观测阶数和相对可观测度定量分析状态的可观测性, 但是上述方法均有一定的局限性[13-14]。

文中在文献[15]的基础上分析在卡尔曼滤波过程中误差协方差阵对对应状态分量的估计误差或精度的影响, 提出了一种基于可观测度反馈的SINS/DVL组合导航算法, 该方法可以有效解决部分状态参数可观测性弱导致的系统滤波精度较低的问题。

1 SINS/DVL组合导航模型

1.1 状态方程

SINS/DVL组合导航系统各状态变量分别选取为:

系统误差状态共22维, 如下

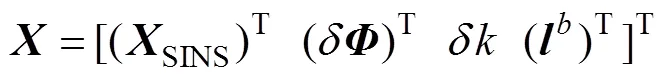
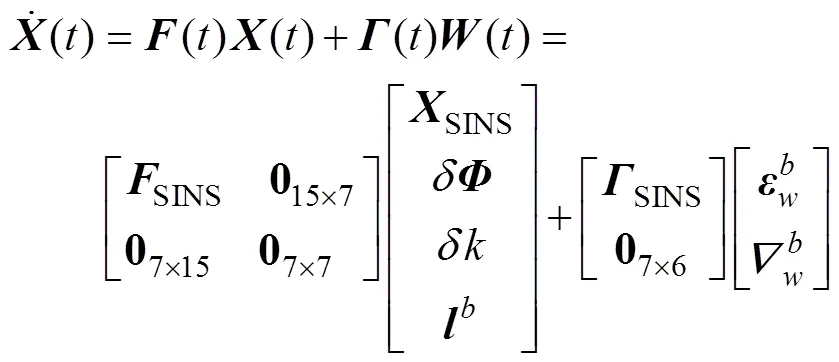
1.2 量测方程

根据上述误差分析可知, DVL实际输出速度

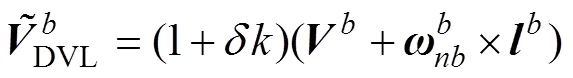
投影到导航坐标系, 可写为

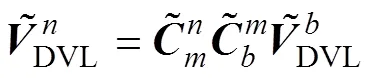
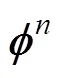
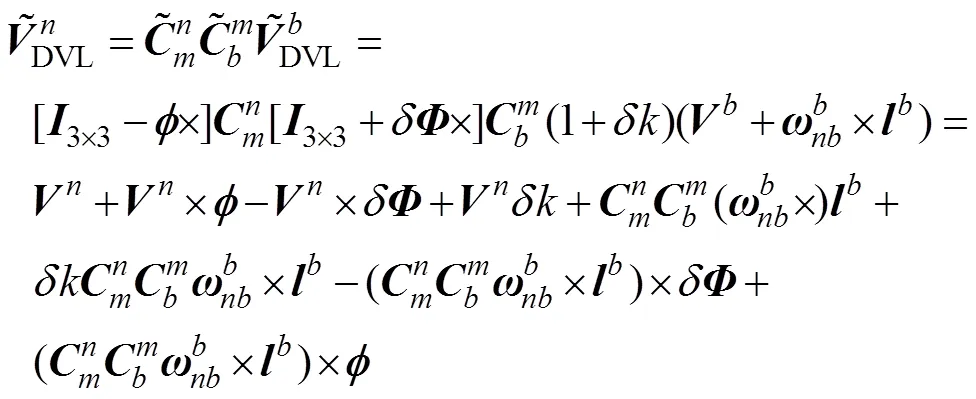
从而可得DVL速度误差

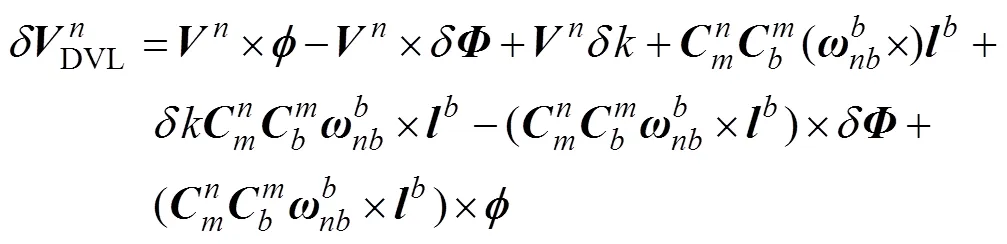
以SINS和DVL输出的速度差值为量测量, 则

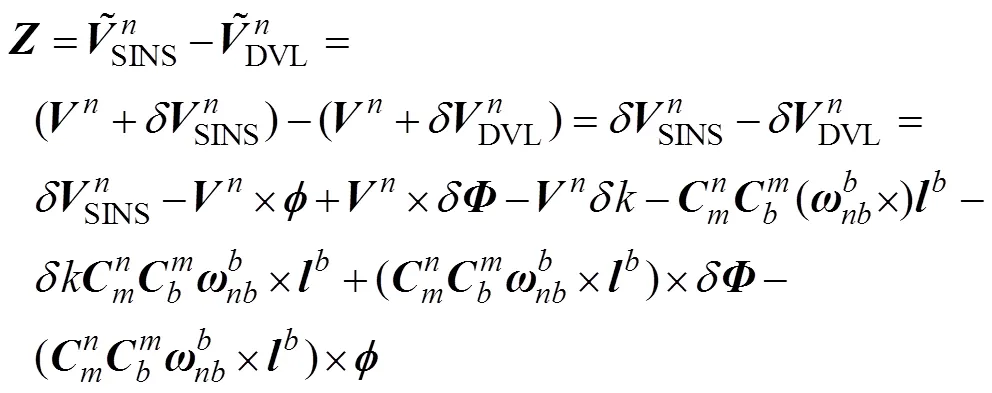
整理可得如下形式的非线性量测方程

2 基于可观测度反馈的SINS/DVL组合导航算法

2.1 基于协方差阵的可观测度分析

可观测度的概念是在可观测性概念的基础上发展而来的, 所以有必要首先明确可观测性的概念。对于有界输入输出线性/非线性系统, 其可观测性定义如下。

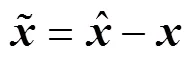
定义

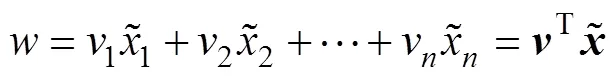
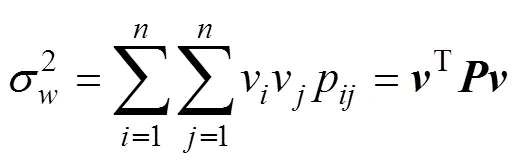
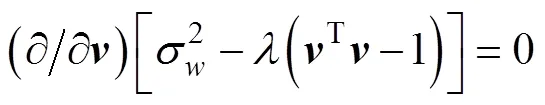
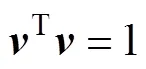
将式(11)代入式(12)得

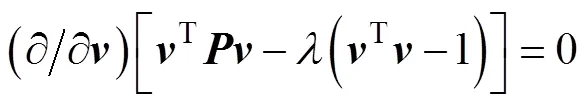
推导可得

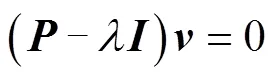
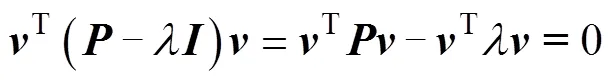
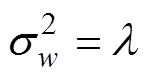
2.2 自适应调节引子计算步骤

在SINS/DVL组合导航系统中, 为了提高系统状态的估计精度, 根据各状态分量在不同时刻可观测度的大小确定该时刻在状态估计中占据的权重系数, 从而构造自适应调节因子, 以减小弱观测度数据对整个滤波器的影响, 提高滤波算法估计精度。下面给出自适应调节因子的具体计算步骤。

1) 通过一致变换使估计误差向量无量纲化

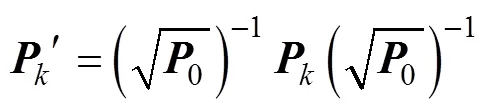
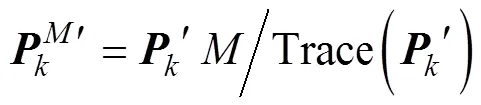
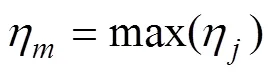
5) 计算各状态变量自适应调节因子

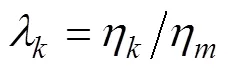
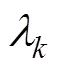
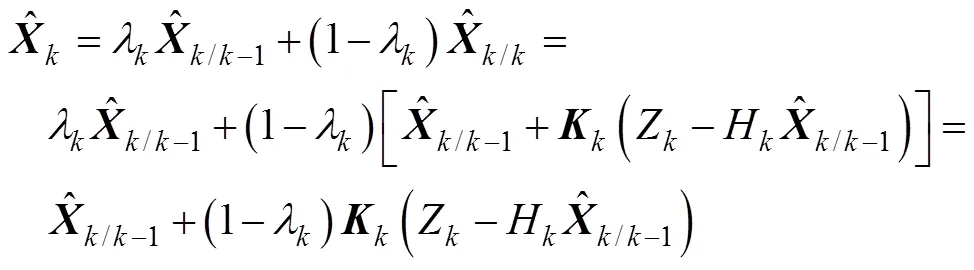
从而实现通过对不同时刻状态变量的可观测度信息来动态调整其增益的目的。

3 仿真结果与分析

为了验证基于可观测度反馈的SINS/DVL组合导航算法的效果, 进行仿真分析。仿真中对全球导航卫星系统定位(global navigation satellite system, GNSS)等传感器参数进行了比较, 如表1所示。

表1 传感器参数

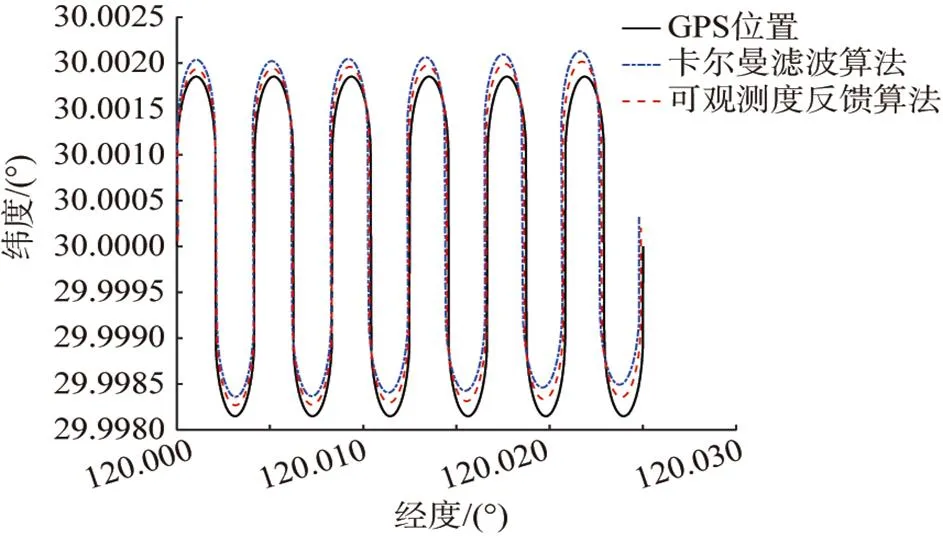
图1 UUV模拟航迹

分别对基于常规卡尔曼滤波和可观测度反馈滤波的SINS/DVL组合导航算法进行仿真, 并实时计算陀螺漂移、加表零偏、SINS的安装误差角和DVL刻度系数误差的可观测度及状态估计值, 结果如图2~图5所示, 2种算法的定位误差见图6。

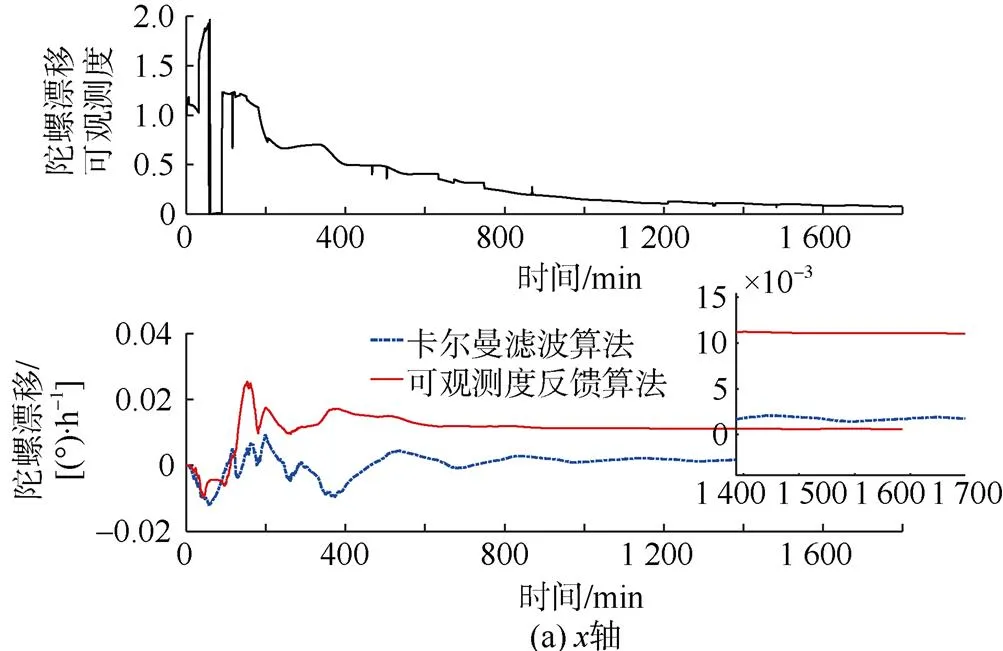
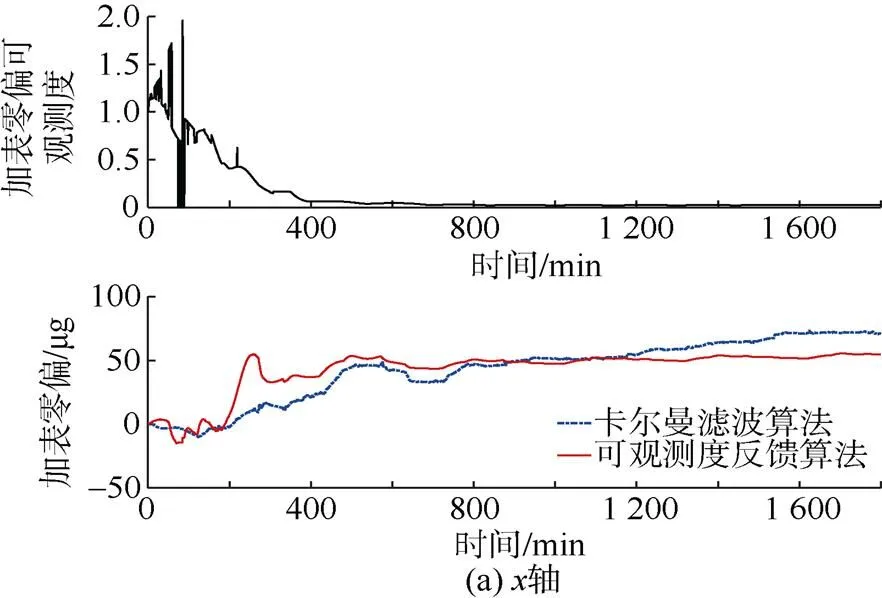
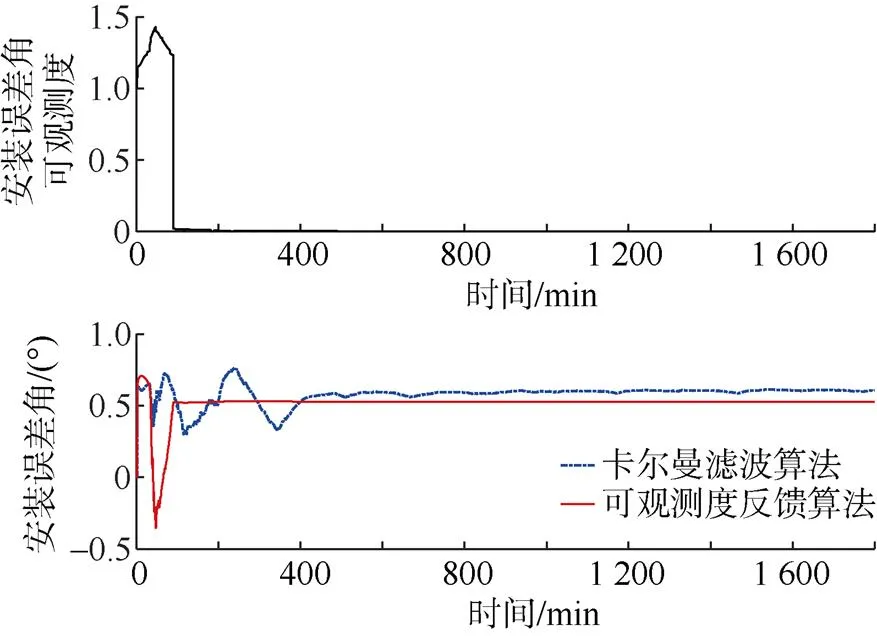
图4 SINS z轴安装角误差可观测度及其估计值

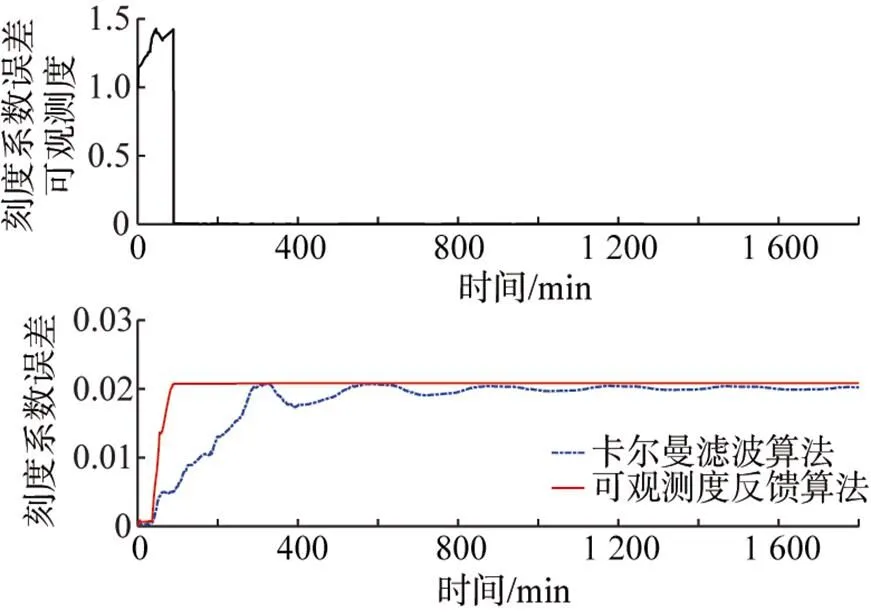
图5 DVL刻度系数误差可观测度及其估计值

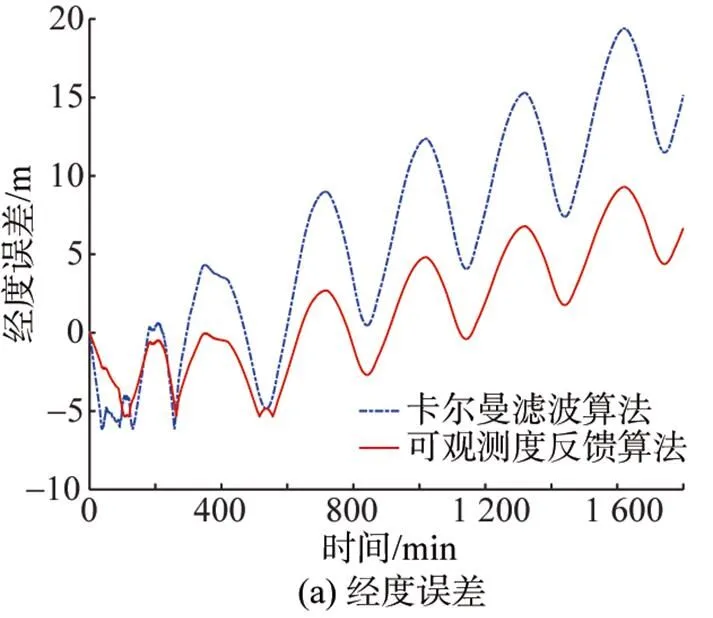
Fig 6 Error of location

从图2和图3可以看出, 与常规卡尔曼滤波算法相比, 采用可观测度反馈滤波算法时, 不仅使陀螺漂移和加表零偏等系统状态估计精度更高,而且收敛速度更快, 特别是在系统状态的可观测度非常小的情况下, 其状态估计值具有更高的稳定性和估计精度。从图4和图5可以看出, 在可观测度反馈滤波算法中, SINS的轴安装角误差和DVL刻度系数误差的可观测度在100 min左右迅速降到非常小的情况, 而其状态估计值也迅速稳定, 具有更好的估计效果。从图6中可以看出, 在定位误差上, 采用可观测度反馈滤波算法的SINS/DVL组合导航定位精度明显优于使用常规卡尔曼滤波算法。

4 试验数据分析

为了验证基于可观测度反馈滤波的SINS/ DVL组合导航算法在湖中试验的效果, 进行湖试数据分析。其中使用的各传感器参数如表1所示。采用的航迹数据为某次湖上试验航行数据, 试验船主要进行1个旋回机动和1个S形机动, 载体速度在3~5 kn之间, 全程航行37.78 km, 总航时4.94 h, 载体轨迹见图7。

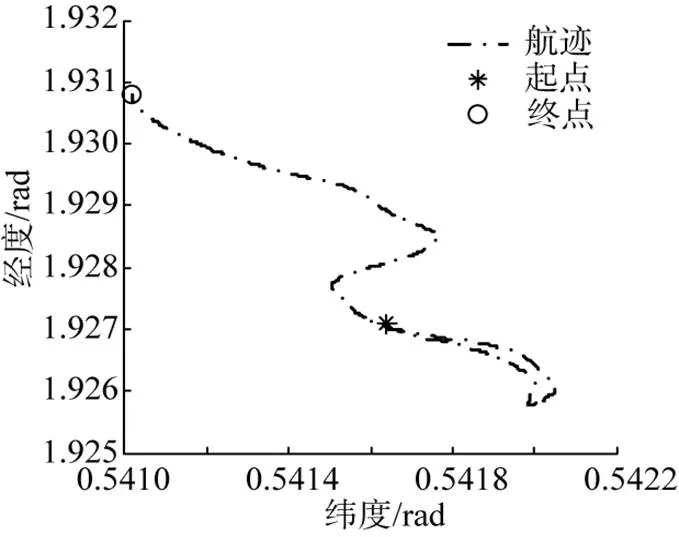
图7 载体轨迹

分别对基于常规卡尔曼滤波和可观测度反馈滤波的SINS/DVL组合导航算法进行仿真, 结果如图8所示。由图8可以看出, 在定位误差上, 采用常规卡尔曼滤波算法, 全程累积误差为333 m, 相对误差为8.8‰, 而采用可观测度反馈滤波算法, 全程累积误差为57 m, 相对误差为1.5‰, 可见可观测度反馈滤波算法累积误差明显小于常规卡尔曼滤波算法。

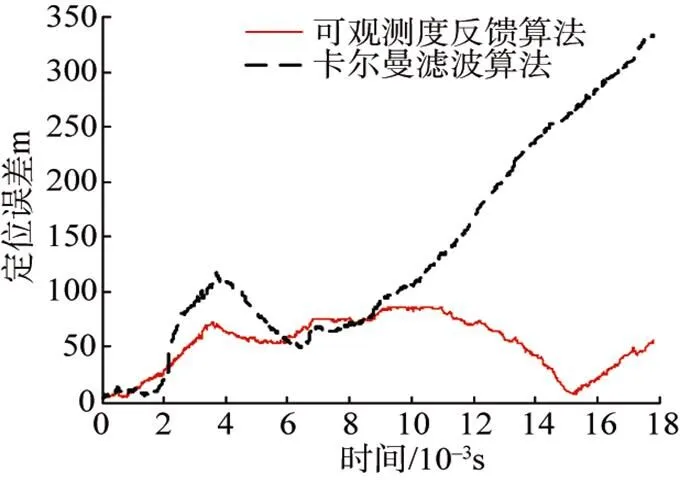
图8 定位误差对比

综上所述, 基于可观测度反馈的SINS/DVL组合导航滤波算法, 通过引入含有系统状态实时可观测度信息的自适应调节因子, 实现了减小状态变量的实时估计误差, 进而提高SINS/DVL组合导航精度的目的。在相同的精度要求下, 可延长水下SINS/DVL组合导航自主航行的时间。

5 结束语

SINS/DVL组合导航是UUV自主航行的主要导航方式。文中针对部分系统状态可观测性却相对较弱的问题, 提出1种基于可观测度反馈滤波算法的SINS/DVL组合导航算法, 根据各状态分量在不同时刻可观测度的大小确定该时刻在状态估计中占据的权重系数, 从而构造自适应调节因子以减小弱观测度数据对整个滤波器的影响, 提高滤波算法估计精度。利用湖试数据对可观测度反馈滤波算法与常规卡尔曼滤波算法进行了对比分析, 从状态变量估计精度和定位误差的角度验证了可观测度反馈滤波算法的效果。在对试验数据进行整理分析过程中发现, 除了系统中可观测度弱的状态参数会影响系统的滤波效果外, 当DVL量测信息中存在较大误差时, 也会降低系统状态参数的估计精度, 因此需要进一步优化滤波算法, 规避大误差量测信息的影响。

[1] 冯正平. 国外自治水下机器人发展现状综述[J]. 鱼雷技术, 2005, 13(1): 5-9.Feng Zheng-ping. A Review of the Development of Autonomous Underwater Vehicles(AUVs) in Western Countries[J]. Torpedo Technology, 2005, 13(1): 5-9.

[2] Hayato K, Tamaki U. Navigation of an AUV for Inves- tigation of Underwater Structures[J]. Control Engineer- ing Practice, 2004, 12(12): 1551-1559.

[3] Yaruui G, Martins R, Sousa J. Accuracy Analysis of DVL/ IMUI Magnetometer Integrated Navigation System using Different IMUs in AUV[C]//Proceedings of the 2010 8th IEEE International Conference on Control and Automation, Xiamen, China: ICCA, 2010: 519-521.

[4] 徐晓苏, 潘永飞, 邹海军. 基于自适应滤波的SINS/ DVL组合导航系统[J]. 华中科技大学学报(自然科学版), 2015, 43(2): 48-53.Xu Xiao-su, Pan Yong-fei, Zou Hai-jun. SINS/DVL Integrated Navigation System Based on Adaptive Filtering[J]. Journal of Huazhong University of Science and Technology(Nature Science Edition), 2015, 43(2): 48-53.

[5] 徐晓苏, 董亚, 童金武, 等. 基于5阶球面最简相径的改进型容积卡尔曼滤波在SINS/DVL组合导航中的应用[J]. 中国惯性技术学报, 2017, 25(3): 343-348.Xu Xiao-su, Dong Ya, Tong Jin-wu, et al. Improved Fifth- degree Spherical Simplex Sadial Cubature Kalman Filter in SINS/DVL Integrated Navigation[J]. Journal of Chinese Inertial Technology, 2017, 25(3): 343-348.

[6] 陈建华, 朱海, 王超, 等. 水下SINS/DVL紧组合导航算法[J]. 海军工程大学学报, 2017, 29(2): 108-112.Chen Jian-hua, Zhu Hai, Wang Chao, et al. Underwater SINS/DVL Tightly Integrated Navigation Algorithm[J]. Journal of Naval University of Engineering, 2017, 29(2): 108-112.

[7] 严涛, 王跃钢, 杨波, 等. SINS/DR组合导航系统可观测性研究[J]. 现代防御技术, 2012, 40(3): 83-87.Yan Tao, Wang Yue-gang, Yang Bo, et al. Observability of SINS/DR Integrated Navigation System[J]. Modern Defe- nce Technology, 2012, 40(3): 83-87.

[8] Goshen-Meskin D, Bar-Itzhack I Y. Observability Analysis of Piece-wise Constant Systems. II. Application to Inertial Navigation In-flight Alignment[J]. IEEE Transac- tions on Aerospace and Electronic Systems, 1992, 28(4): 1068-1075.

[9] Wu Y X, Wu M P, Hu X P. Self-calibration for Land Navigation Using Inertial Sensors and Odometer: Observability Analysis[C]//AIAA Guidance, Navigation and Control Conference, Chicago, Illinois, USA: AIAA, 2010: 964- 969.

[10] 帅平, 陈定昌, 江涌. GPS/SINS组合导航系统状态的可观测度分析方法[J]. 宇航学报, 2004, 12(2): 219-224．Shuai Ping, Chen Ding-chang, Jiang Yong. Observable Degree Analysis Method of Integrated GPS/SINS Navigation System[J]. Journal of Astronautics, 2004, 12(2): 219- 224.

[11] 杨晓霞, 黄一. 外场标定条件下捷联惯导系统误差状态可观测性分析[J]. 中国惯性技术学报, 2008, 16(6): 1-8.Yang Xiao-xia, Huang Yi. Observability Analysis for the Error States of SINS Under the Outer Field Conditions[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 1-8.

[12] 孔星炜, 董景新, 吉庆昌, 等. 一种基于PWCS的惯导系统可观测度分析方法[J]. 中国惯性技术学报, 2011, 19(6): 631-636.Kong Xing-wei, Dong Jing-xin, Ji Qing-chang, et a1. INS Observability Degree Analysis Method Based on PWCS [J]. Journal of Chinese Inertial Technology, 2011, 19(6): 631-636.

[13] 马艳红, 胡军. 基于SVD理论的可观测度分析方法的几个反例[J]. 中国惯性技术学报, 2008, 16(4): 448-457.Ma Yan-hong, Hu Jun. Counterexamples for Degree of Observability Analysis Method Based on SVD Theory[J]. Journal of Chinese Inertial Technology, 2008, 16(4): 448- 457.

[14] 杨晓霞, 阴玉梅. 可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J]. 中国惯性技术学报, 2012, 20(4): 405-409.Yang Xiao-xia,Yin Yu-mei. Discussions on Observability and Its Applications in SINS[J]. Journal of Chinese Iner- tial Technology, 2012, 20(4): 405-409.

[15] Ham F M, Brown T G. Observability, Eigenvalues, and Kalman filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, 19(2): 269-273.

[16] 章大勇. 激光雷达-惯性组合导航系统的一致性与最优估计问题研究[D]. 长沙: 国防科学技术大学, 2010.

The SINS/DVL Integrated Navigation Algorithm Based on Observable Degree Feedback

LI Zhi-wei1, YUE Wei2, GAO Sheng-feng2, CAI Peng2, ZHU Hai-rong2

(1. 91001thUnit, the People’s Liberation Army of China, Beijing 100080, China; 2. Navy Submarine Academy, Qingdao 266199, China)

Aiming at the problem that some system states in strap-down inertial navigation system(SINS)/Doppler velocity log(DVL) integrated navigation have significant influence on navigation accuracy but have relatively weak observability, a SINS/DVL integrated navigation algorithm based on observable degree feedback is proposed. The algorithm quantitatively analyzes the observability of each state parameter of the system, and constructs an adaptive factor based on observability feedback according to the fact that the observability of the system state parameters depends on maneuver states in order to increase the estimated proportion of state parameters when they have high observable degree, and so as to improve the adaptability and accuracy of the algorithm. The performance of the proposed algorithm is verified through lake trial, and the results show that the accumulated error of this observable degree feedback filtering algorithm is obviously smaller than that of the conventional Kalman filter algorithm, and the autonomous navigation time of the SINS/DVL integrated navigation can be prolonged under the same accuracy requirement.

unmanned undersea vehicle(UUV); integrated navigation; strap-down inertial navigation system(SINS); Doppler velocity log(DVL); observable degree

TJ630; U666.1

A

2096-3920(2020)02-0155-07

10.11993/j.issn.2096-3920.2020.02.006

2019-4-17;

2019-07-28.

李志炜(1979-), 男, 本科, 高工, 主要研究方向为导航时频技术.

李志炜, 岳崴, 高胜峰, 等. 基于可观测度反馈的SINS/DVL组合导航算法[J]. 水下无人系统学报, 2020, 28(2): 155-161.

(责任编辑: 杨力军)