聚合物/降黏剂复合驱产液能力动态预测方法

姜颜波，刘 璐，元福卿，潘玉萍，祝仰文，魏翠华，李 峰

（1.中国石化油田勘探开发事业部，北京 100035；2.中国石油大学（华东）石油工程学院，山东青岛 266580；3.中国石化胜利油田分公司勘探开发研究院，山东东营 257015；4.中国石化北京埕岛西项目部，北京 100035）

1 聚合物/降黏剂复合驱产液能力表征

1.1 产液能力评价指标

对于聚合物/降黏剂复合驱区块，其生产井产液能力的变化主要是与注入化学剂前的产液能力进行对比。因此，采用无因次产液指数作为聚合物/降黏剂复合驱产液能力的评价指标，其表达式为：

1.2 无因次产液指数曲线变化规律

注入的化学剂由注入井运移至生产井需要一定的时间，因此在注入化学剂初期产液指数仍然遵循水驱时的规律，呈继续上升趋势。但当所注入的高黏度聚合物和降黏剂达到一定量时，生产井的产液能力开始下降，在后续水驱阶段，随着低黏度水的稀释和冲刷，渗流阻力下降至低峰值后又不断恢复。仅从产液指数开始下降时进行研究，产液指数的变化规律表现为无因次产液指数曲线在实施化学驱后整体呈现漏斗形，并可分为2个阶段：注入化学剂阶段和后续水驱阶段（图1）。为了定量表征无因次产液指数曲线的变化规律，定义T1，ΔJ1，ΔJmin，Tmin，ΔJmax和Tmax共6个特征参数。

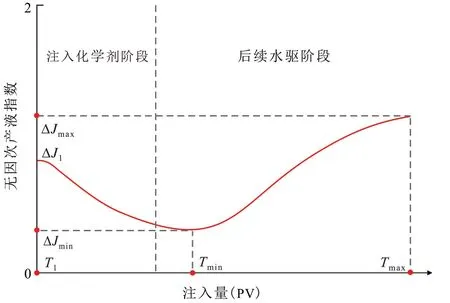
图1 聚合物/降黏剂复合驱无因次产液指数曲线变化Fig.1 Schematic diagram of dimensionless liquid production index in polymer/viscosity reducer compound flooding

1.3 无因次产液指数定量表征模型

如图1 所示，聚合物/降黏剂复合驱无因次产液指数曲线通常呈现不对称性。为了描述这种不对称性，引入几何学中的不对称偏差项，其表达式为：

σ值越趋近于1，无因次产液指数曲线的对称性越好；反之，则曲线的不对称性越强。

对于偏漏斗形的无因次产液指数曲线，在几何学中可表征为：

（3）式中基于矿场实际设定的ΔJmax的上限值为1.4，其与储层性质相关。

本文提出了一种基于矩阵补全的无线传感器网络数据收集方案.通过将传感器网络数据收集问题转换为低秩矩阵分解问题,并依据Johnson-Lindenstrauss引理对Kaczmarz迭代中的投影操作降维,从而提高了矩阵补全算法的重构性能.在仿真实验中,分别利用合成数据集和真实数据集测试和分析了所设计的矩阵补全算法在重构精度、成功重构概率以及重构时间等方面的性能指标.下一步研究方向将着重考虑结合概率近似方法进一步提高矩阵补全算法的重构性能.

对于一个特定的区块，其生产井产液指数的变化与注入化学剂的质量浓度、化学剂注入段塞尺寸以及降黏剂性质等有关，各待定系数与这些参数存在函数关系，即：

为了得到（4）式的具体表达式，首先对影响产液指数的各因素进行分析，然后采用正交试验设计方法进行方案设计，并基于试验结果，采用Levenberg-Marquardt（LM）算法对各参数进行多元非线性回归，进而得到无因次产液指数定量表征模型［19-21］。

2 应用实例

2.1 数值模拟模型建立

以孤岛油田东区Ng3—4单元为目标区块，模拟区域的含油面积约为0.72 km2，平均有效油层厚度为18.92 m，石油地质储量约为386.58×104t，油层埋深为1 200～1 305 m，油藏温度为71 ℃，初始地层压力为12.5 MPa，平均孔隙度为34%，孔隙体积为4 621×104m3，平均渗透率为1 138 mD，渗透率变异系数为0.7，原始含油饱和度为61%，地层原油黏度为573 mPa·s，地层水矿化度为5 694 mg/L。数值模拟模型共划分为7个模拟层，采用直角坐标网格，总网格数为81 900个，网格步长为50 m。

孤岛油田东区Ng3—4单元于1975年8月投产，先后经历了水驱开发和化学驱开发2个阶段。为了得到与现场实际相符合的化学驱模拟效果，在CMG模拟软件中，考虑聚合物的吸附、降解、黏度与质量浓度关系等因素，聚合物溶液的黏度与质量浓度关系曲线以及油、水相相对渗透率曲线如图2 和图3所示。结合矿场实际情况，数值模拟模型选取的基础方案为：1975年8月模型投产，经历注水开发后于2011 年5 月转入聚合物/降黏剂复合驱阶段，聚合物质量浓度为2 000 mg/L，降黏剂质量分数为0.4%，降黏剂降黏率为90%。当化学剂注入段塞达到0.4 PV时转为后续水驱开发，当区块综合含水率达到98%时模拟终止。

图2 数值模拟模型中聚合物溶液黏度与质量浓度关系曲线Fig.2 Relationship between viscosity and mass concentration of polymer solution in numerical model

图3 数值模拟模型中油水相对渗透率曲线Fig.3 Oil-water relative permeability curve in numerical model

2.2 无因次产液指数影响因素

当目标油藏确定后，其储层参数即已固定，此时生产井产液指数的影响因素主要为化学剂性质参数，因此，选取化学剂注入段塞尺寸、聚合物质量浓度、降黏剂质量分数以及降黏剂降黏率共4 个主要因素，利用单因素分析法研究其对无因次产液指数的影响。各单因素的变化范围如表1所示。

表1 无因次产液指数影响因素取值Table1 Influencing factors of dimensionless liquid production index

2.2.1 化学剂注入段塞尺寸

分析化学剂注入段塞尺寸对无因次产液指数的影响（图4a）可以看出，注入化学剂后生产井的无因次产液指数普遍下降，注入化学剂前期各曲线几乎重合，但在后期化学剂注入段塞尺寸会对无因次产液指数曲线的抬升幅度产生较大影响，注入量越低，曲线后期的抬升幅度越大。同时化学剂注入段塞尺寸对曲线的漏斗宽度也有较大影响，化学剂注入段塞尺寸越大，漏斗宽度也越大。这是因为随着化学剂注入段塞尺寸的增大，化学剂溶液的波及范围扩大，渗流阻力逐渐增大，从而影响采出井的产液能力，化学剂注入段塞尺寸越大，吸附在岩石表面的化学剂质量浓度越高，残余阻力也越大，因此后期无因次产液指数的恢复速率和恢复程度越低。从无因次产液指数的统计结果（图4b）可以看出，其最低可降至约为0.3，说明高段塞时生产井的产液能力最低可降至原来的三分之一。

图4 化学剂注入段塞尺寸对无因次产液指数的影响Fig.4 Effect of injection slug size of chemical agent on dimensionless liquid production index

2.2.2 聚合物质量浓度

从聚合物质量浓度对无因次产液指数的影响（图5）可以看出，与化学剂注入段塞尺寸所造成的影响不同，注入化学剂后各曲线前期不重合，即聚合物质量浓度对无因次产液指数曲线的影响表现在整个注入化学剂和后续水驱阶段。聚合物质量浓度越高，无因次产液指数的最小值和最终值均越小，这主要是因为聚合物质量浓度越高，对应的化学剂溶液黏度也越高，流动阻力越大，因此产液能力降幅相应也越大。在后续水驱阶段，由于低黏度水的稀释和驱替作用，生产井附近的化学剂质量浓度逐渐降低，无因次产液指数不断恢复，且低质量浓度聚合物所对应生产井的产液指数的恢复速度明显较快。

2.2.3 降黏剂质量分数

图5 聚合物质量浓度对无因次产液指数的影响Fig.5 Effect of polymer mass concentration on dimensionless liquid production index

降黏剂质量分数对无因次产液指数的影响与化学剂注入段塞尺寸、聚合物质量浓度不同，降黏剂质量分数主要对无因次产液指数曲线的前期形态影响较大，而在化学驱后期曲线趋向于一致（图6）。降黏剂质量分数越高，化学驱前期无因次产液指数降幅越小，这主要是因为降黏剂可以大幅降低原油黏度。降黏剂质量分数越高，原油在地层中流动时的黏滞阻力越小，无因次产液指数的下降幅度也越小。同时，由于目前化学驱所采用降黏剂的降黏率一般在90%以上，降黏效果较好，因此降黏剂达到一定质量分数后，继续升高质量分数对无因次产液指数的影响较小。对比化学剂注入段塞尺寸、聚合物质量浓度和降黏剂质量分数对无因次产液指数的影响可以看出，降黏剂质量分数对无因次产液指数的影响程度远低于聚合物质量浓度和化学剂注入段塞尺寸。

2.2.4 降黏剂降黏率

由降黏剂降黏率对无因次产液指数的影响（图7）可以看出，降黏剂降黏率对注入化学剂和后续水驱阶段的无因次产液指数均会产生影响。降黏率越高，地层中的原油黏度降低幅度越大，因此其流动性越好，注入化学剂后生产井的产液能力也越高。但总体上，降黏剂降黏率对无因次产液指数的影响远小于聚合物质量浓度和化学剂注入段塞尺寸。

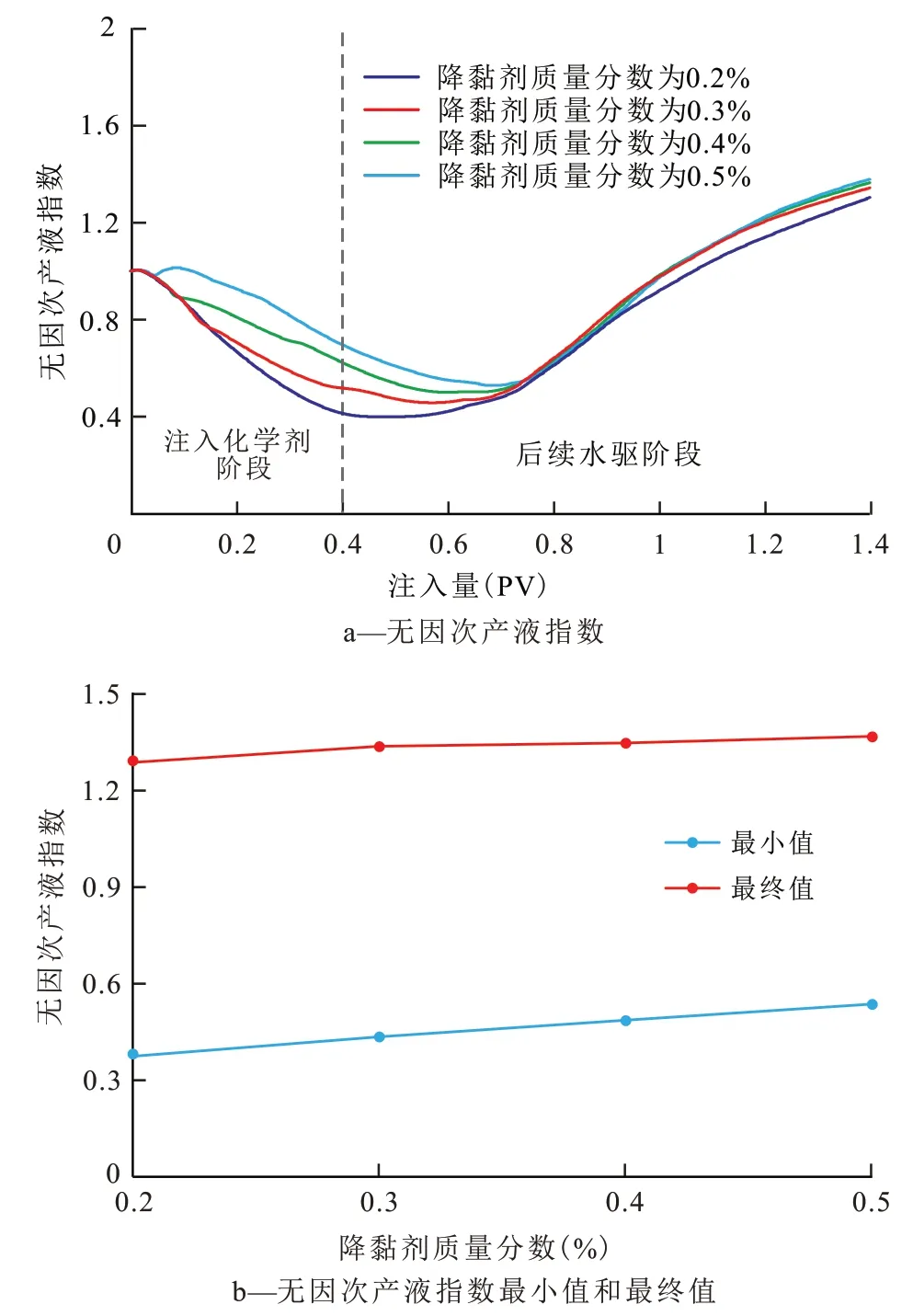
图6 降黏剂质量分数对无因次产液指数的影响Fig.6 Effect of mass fraction of viscosity reducer on dimensionless liquid production index

2.3 无因次产液指数定量表征

2.3.1 模型的建立

无因次产液指数影响因素的研究结果表明，所选取的化学剂注入段塞尺寸、聚合物质量浓度、降黏剂质量分数和降黏剂降黏率这4个影响因素均会对无因次产液指数曲线的形态产生一定影响，各曲线的初始值几乎相同，且开始下降时刻也几乎相同，而（3）式中的系数a和c分别与曲线的初始值及下降时刻相关。对图4—图7中的所有曲线采用（3）式进行拟合，发现各曲线所对应的a和c值变化范围很小，因此对系数a和c分别取值为0.032 和3.778，但对应的系数b，d和f的变化幅度均较大，则无因次产液指数定量表征模型可表示为：

由（5）式可知，仅需建立b，d和f与上述4 个影响因素之间的定量关系，即可得到无因次产液指数定量表征模型。

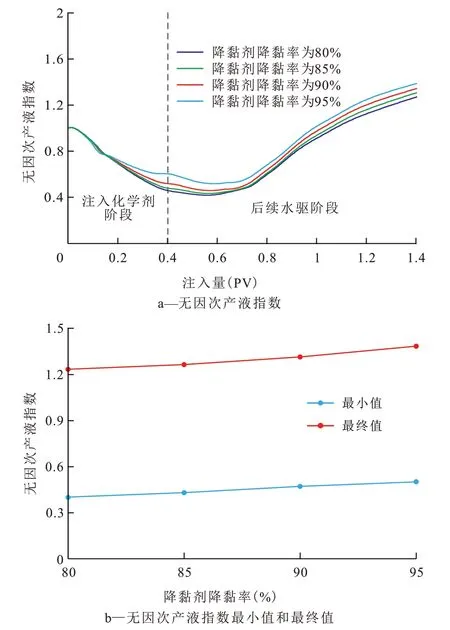
图7 降黏剂降黏率对无因次产液指数的影响Fig.7 Effect of viscosity reducer on the dimensionless liquid production index

以化学剂注入段塞尺寸为例，研究不同化学剂注入段塞尺寸所对应的b，d和f的取值分布（图8），可以看出b和f与化学剂注入段塞尺寸之间呈现良好的二次函数关系，而d与化学剂注入段塞尺寸之间呈现良好的线性关系。同理可分析b，d和f与聚合物质量浓度、降黏剂质量分数以及降黏剂降黏率之间的关系，结果表明：b与聚合物质量浓度和降黏剂降黏率之间均呈现良好的二次函数关系，与降黏剂质量分数之间呈现良好的线性关系；d与聚合物质量浓度、降黏剂质量分数之间呈现良好的二次函数关系；f与降黏剂降黏率之间呈现良好的二次函数关系，与聚合物质量浓度、降黏剂质量分数之间呈现良好的线性关系，由此可以得到各系数的回归关系式为：

图8 化学剂注入段塞尺寸与无因次产液指数定量表征模型中主控系数的关系Fig.8 Relationship between injection slugs size of chemical agent and main controlling coefficients in quantitative characterization model for dimensionless liquid production index

根据多元非线性回归原理，采用正交试验设计得到（6）式中各多项式系数。采用4 因素4 水平共计16组试验方案进行后续分析和回归，各因素的水平取值如表2 所示。对16 组试验方案所对应的无因次产液指数曲线采用（6）式进行回归，可得到各方案对应的b，d和f值（表3）。

表2 无因次产液指数影响因素水平取值Table2 Level of influencing factors of dimensionless liquid production index

表3 正交试验设计结果Table3 Design results of orthogonal experiments

将正交试验设计得到的b，d和f值代入（6）式中，采用LM 法进行多元非线性回归，可得到b，d和f的表达式为：

采用（7）式计算对应16 组正交试验方案的b，d和f多元线性回归值，并与表3中的曲线拟合值进行对比，结果（图9）表明，不同试验方案下b，d和f的曲线拟合值与多元非线性回归值在y=x左右两侧分布，表明二者之间存在良好的相关性，多元非线性回归拟合的多项式精度较高。因此，当已知油藏化学驱参数时，可直接代入（7）式中得到b，d和f值，然后根据（5）式即可直接得到无因次产液指数的表达式及其所对应的分布曲线。

2.3.2 模型的验证及分析

在各因素的水平取值范围内随机挑选与正交试验方案不重合的4 组方案进行数值计算，将模拟曲线与无因次产液指数定量表征模型所预测的曲线进行比对分析，用以验证所建立无因次产液指数定量表征模型的准确性。选取的4组验证方案如表4 所示，由不同方案下模拟曲线与无因次产液指数定量表征模型预测曲线对比（图10）可以看出，不同方案下无因次产液指数定量表征模型预测曲线与模拟曲线具有良好的匹配性，表明无因次产液指数定量表征模型的预测精度较高，可以满足矿场预测的需要。

图9 主控系数的曲线拟合值与无因次产液指数定量表征模型中多元非线性回归值对比Fig.9 Comparison between fitting values of main controlling factors and coefficients with multiple nonlinear regression in quantitative characterization model for dimensionless liquid production index

表4 验证方案Table4 Verification cases

中国胜利、大庆等油田普遍采用的聚合物驱、强化聚合物驱、二元驱、三元驱、凝胶驱甚至泡沫驱等化学驱方式均是通过改善流度比以扩大波及系数，在化学剂注入后无因次产液指数均会出现明显下降；但在后续水驱阶段，由于化学剂的产出以及吸附、降解，导致驱替液中的化学剂质量浓度不断降低，无因次产液指数不断恢复，因此在上述化学驱过程中均会表现出无因次产液指数先降低后升高的偏漏斗形曲线分布特征。所建立的无因次产液指数定量表征模型中的（3）式为偏漏斗形曲线的通式，因此可以直接推广为上述各种化学驱方式无因次产液指数曲线的预测模型，但该式中各系数的取值与化学剂的物化参数有关，因此在推广应用时需考虑其物化特征对无因次产液指数的影响，通过多元非线性回归分析确定（3）式中各系数的表达式，进而得到可靠的无因次产液指数预测模型。

图10 无因次产液指数定量表征模型预测曲线与模拟曲线对比Fig.10 Comparison between prediction curves and simulation curves of dimensionless liquid production index in quantitative characterization model

3 结论

利用数理统计原理和油藏数值模拟方法，建立一套聚合物/降黏剂复合驱产液能力的动态预测方法。该方法以无因次产液指数作为评价指标，根据数值模拟结果，采用多元非线性回归方法得到无因次产液指数定量表征模型，进而得到目标区块在不同化学驱方案下的产液指数变化曲线，为聚合物/降黏剂复合驱的方案设计提供了支持和帮助。无因次产液指数影响因素的分析结果表明，无因次产液指数曲线在实施化学驱后整体呈现先下降再上升的偏漏斗形；化学剂注入段塞尺寸在注入化学剂前期对无因次产液指数的影响较小，但在后期主要影响无因次产液指数的恢复程度；与之相反，降黏剂质量分数则主要对无因次产液指数曲线的前期形态影响较大，聚合物质量浓度和降黏剂降黏率对无因次产液指数曲线的前期和后期均有一定程度的影响，但以聚合物质量浓度对无因次产液指数的影响程度更大。模型验证结果表明，所建立的无因次产液指数定量表征模型预测曲线与模拟曲线具有良好的匹配性，证明建立的无因次产液指数定量表征模型的预测精度较高，可以满足矿场预测的需要。

符号解释

ΔJ——无因次产液指数；J——产液指数，m3/（d·MPa）；J0——注入化学剂前的产液指数，m3/（d·MPa）；q——生产井的日产液量，m3/d；pa——地层平均压力，MPa；pwf——生产井的井底流动压力，MPa；T1——无因次产液指数初始下降时刻，a；ΔJ1——T1对应的ΔJ的局部极大值；Tmin——ΔJmin对应的时刻，a；Tmax——ΔJmax对应的时刻，a；σ——不对称偏差项；a，b，c，d，f——模型中的待定系数，其中，a与ΔJ1有关，b与ΔJmin有关，c与T1有关，d与Tmin有关，f与σ有关；T——累积注入量，PV；f(X1)，f(X2)，f(X3)，f(X4)——无因次产液指数定量表征模型主控系数与影响因素X1，X2，X3，X4之间的回归式；x1——化学剂注入段塞尺寸，PV；x2——聚合物质量浓度，mg/L；x3——降黏剂质量分数，%；x4——降黏剂降黏率，%；a0—a7，m0—m5，n0—n6——多项式系数。