页岩气体积压裂水平井试井解释新模型

徐中一，方思冬，张 彬，刘银山，刘 华，戴 城

（1.中国石化石油勘探开发研究院，北京 100083；2.中国石油长庆油田分公司对外合作部，陕西西安 710018；3.陕西延长石油（集团）有限责任公司研究院，陕西西安 710065）

中国页岩气资源潜力巨大［1］但储层基质非常致密［2-4］，随着压裂技术的革新［5］，体积压裂水平井技术已经成为中国非常规油气藏开发的关键技术［6］。微地震监测技术显示，在体积压裂之后，储层中形成了复杂的裂缝网络。然而，通过微地震数据只能获得压裂改造区的大致形态，并不能获得准确裂缝网络信息。试井是一种获取储层信息的重要手段，通过试井资料的解释，可以反演并得到影响气井产量的关键参数，对储层评价、压裂评价和动态预测具有重大意义［7-9］。

目前，针对体积压裂水平井，很多学者提出了大量的试井模型。由于体积压裂水平井一般都展现出较长的线性流，因此大部分的模型都基于线性流假设。WATTENBARGER 认为基质流体线性流向裂缝，并由此建立了线性流模型［10］，之后很多改进模型都基于这个假设。BELLO 等将基质考虑成双重介质模型，改进了线性流模型［11］。NOBAKHT等运用此模型进行了产能分析［12-16］。AL-AHMADI等在BELLO 模型的基础上考虑压裂改造后形成的次生裂缝，建立了体积压裂水平井三孔模型［17］。BROHI 等考虑了压裂未改造区的影响，建立了三线性流模型［18-19］。STALGOROVA 等进一步考虑各级压裂之间的不完全改造，建立了五区模型，并假设每个区域内流体均为线性流［20］。JIA 等考虑页岩储层中出现的多相流问题，分别建立了气水两相、油气两相渗流数学模型［21-22］。上述模型仅仅对体积压裂水平井的产能动态特征进行了分析，没有进行试井分析。中国很多油气田采用试井进行储层评价，张奇斌等对压裂直井试井方法进行了研究［23-24］，李树松等针对多段压裂水平井，提出了试井解释平板缝模型［25-27］，王飞等进一步提出了新的试井解释反卷积方法［28］。朱光普等运用平板缝模型，分别考虑页岩气的吸附解吸、负表皮效应和改造外区等因素，进行了试井解释分析［29-31］。方思冬等针对大尺度裂缝的非均质性，建立了离散裂缝渗流数值模拟方法［32］。

图1 体积压裂水平井复杂裂缝网络概念模型Fig.1 Schematic of complex fracture network model for horizontal wells by stimulated reservoir volume

目前，虽然前人针对体积压裂水平井提出了很多试井分析模型，但这些模型都是基于平板缝模型建立的，没有考虑次生裂缝对试井的影响。笔者在考虑人工裂缝和次级裂缝网络的基础上，建立体积压裂水平井试井解释新模型，推导模型的解析解，运用数值模拟对模型进行验证。并基于建立的新模型，分析缝网参数在试井图版上的响应，为体积压裂水平井缝网参数的试井解释提供依据。

1 物理模型

储层在经过大规模水力压裂后，通常在人工裂缝附近可形成非常复杂的次生裂缝网络（图1）。由于裂缝网络的复杂性，每条裂缝均有方位、长度、宽度和导流能力等参数，在试井分析时不可能做到准确拟合。因此，采用正交缝网模型，将近井区域的裂缝网络处理成正交缝网，并认为基质中的流体通过线性流进入次生裂缝，再由次生裂缝系统线性流入人工裂缝，最后由人工裂缝线性流入井筒。其他假设如下：①储层均质、等厚、上下封闭；②考虑流体在储层和裂缝中均为单相、非稳态流动；③流体和岩石为微可压缩；④裂缝等长且以水平井轴对称；⑤由于基质渗透率低，假定流体由基质向次生裂缝的流动为非稳态流动，由次生裂缝向人工裂缝的流动为拟稳态流动。

2 数学模型及求解

2.1 模型基本参数定义

为了便于模型推导，对基本参数及无因次参数进行定义，包括气体拟压力、拟时间、无因次时间、无因次压力、基质储容比、次生裂缝储容比、人工裂缝储容比、基质-次生裂缝传质系数、次生裂缝-人工裂缝传质系数、X方向无因次长度、Y方向无因次长度、Z方向无因次长度，其表达式分别为：

2.2 渗流数学模型

模型中的基质、次生裂缝、人工裂缝通过流量源汇项和边界条件进行耦合，模型假定基质和次生裂缝连接处的压力相等，次生裂缝和人工裂缝连接处压力相等。

2.2.1 基质渗流模型

在基质中，其渗流模型与常规类似，控制方程为：

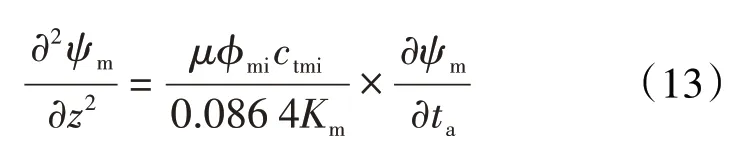
根据模型假设，流体经基质流入次生裂缝中，外边界即为次生裂缝中的压力，其表达式为：

同时，内边界封闭，其表达式为：

2.2.2 次生裂缝渗流模型

考虑到基质向次生裂缝中的流量供给和次生裂缝向人工裂缝的液量供给，次生裂缝的渗流方程为：

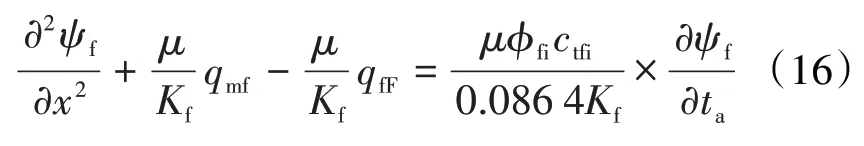
由于基质的渗透率较低，流体由基质向次生裂缝的窜流为非稳态窜流，单位体积基质向次生裂缝的供给流量为：

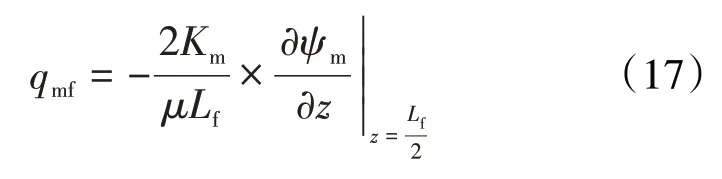
根据假设，次生裂缝与人工裂缝之间为拟稳态窜流，其方程为：

因此，考虑次生裂缝向人工裂缝的拟稳态流假设，忽略（16）式中左边第一项，并代入（17）—（19）式，获得次生裂缝的渗流方程为：

根据假设，流体从次生裂缝流入人工裂缝中，其外边界即为人工裂缝中的压力，其表达式为：

同时，内边界封闭，其表达式为：

2.2.3 人工裂缝渗流模型

考虑到次生裂缝向人工裂缝的流量供给，人工裂缝的渗流方程为：

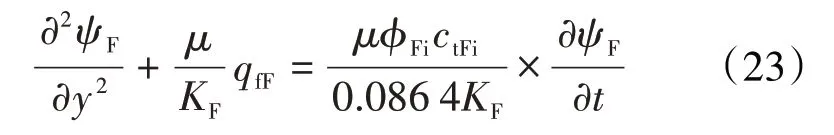
因此，将（17）和（19）式代入（16）式中，可以进一步推导出人工裂缝的渗流方程为：

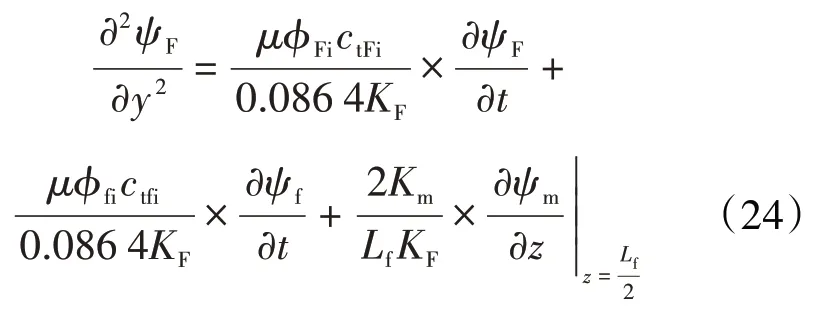
人工裂缝的外边界封闭，其表达式为：

同时，内边界为定产生产，其表达式为：

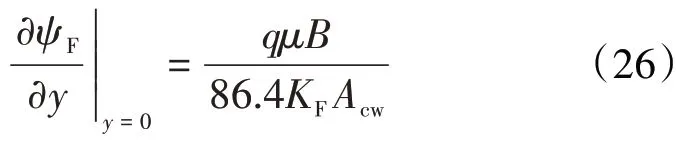
2.2.4 渗流模型无因次化

运用所定义的无因次参数，推导出基质、次生裂缝、人工裂缝渗流模型的无因次形式分别为：

2.3 模型求解

对于（27）—（29）式定义的模型，运用Laplace变换进行求解。

当定产生产时，求解得到Laplace空间下井底流压解为：

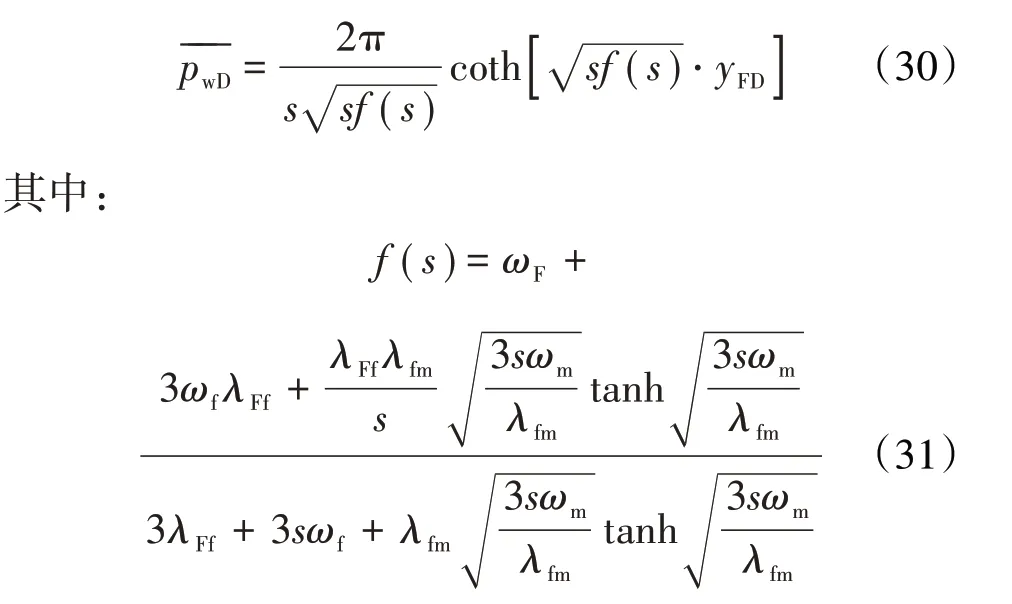
定压生产时，Laplace 空间产量解与定产生产Laplace空间下的无因次井底流压的关系为：

在Laplace空间下，考虑井筒存储效应和表皮效应的井底流压解为：

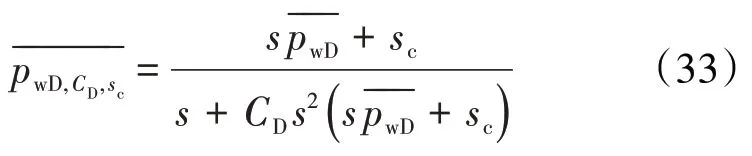
（33）式为模型在Laplace 空间的解，运用Stehfest反演方法进行逆变换，从而将Laplace空间的解转换到实空间。

3 模型验证与应用

3.1 模型验证

为了验证模型的准确性，以一口页岩气体积压裂水平井为例，运用数值模拟软件Eclipse 对模型进行验证。

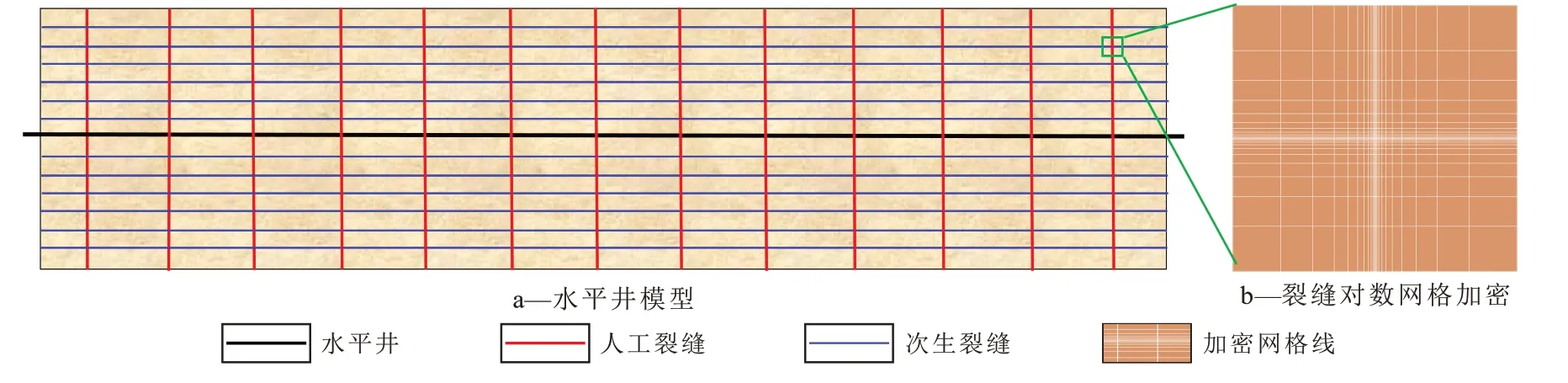
图2 数值模拟验证模型示意Fig.2 Schematic of numerical model for validation

水平井模型见图2a，水平井压裂13 段，用正交缝网模拟形成的复杂缝网，次生裂缝垂直于人工裂缝，且均匀分布在整个改造区内，次生裂缝密度为10 m/条。利用数值模拟对裂缝通过对数网格加密进行表征（图2b）。为了避免井储效应掩盖流动阶段，井储效应系数和表皮系数取值较小，以展示出更多的流动阶段。其他模型相关参数见表1。为了模拟试井过程，页岩气井以500 m³/d定产生产，获得该生产制度下的井底流压数据；再对生产时间和流压数据进行无因次化，以此验证模型的准确性。

表1 数值模拟验证模型参数Table1 Parameters of the numerical model for validation

从模型计算结果与数值模拟结果（图3）对比可以看出，除了由于导数更加敏感，在早期的吻合度稍差外，二者的压力数据基本吻合，表明所建立的数学模型计算可靠，可以用于压裂水平井复杂缝网条件下的试井解释分析。根据试井曲线流动特征，将流动阶段划分为5个阶段：Ⅰ为井筒储集阶段，在此阶段由于受井储效应的影响，压力曲线、压力导数曲线均表现为斜率为1的直线。Ⅱ为人工裂缝线性流阶段，流动初期流体在人工裂缝中的线性流在双对数诊断图上表现为无因次拟压力导数曲线为1/2斜率的直线段。Ⅲ为次生裂缝-人工裂缝窜流阶段，由于人工裂缝流动能力高于次生裂缝的流动能力，存在一个次生裂缝向人工裂缝窜流的阶段。Ⅳ为基质线性流阶段，在流动中后期，产生基质向裂缝的线性流动，该流动段的无因次拟压力导数曲线在双对数图上为1/2 斜率的直线段，这是一般生产过程中出现最多的阶段，其持续时间长。Ⅴ为边界控制流阶段，指压力波传播到封闭外边界以后，地层中出现拟稳态流动，双对数诊断图上表现为无因次拟压力导数曲线上翘，并与无因次拟压力曲线重合，且斜率为1。

图3 数值模拟验证结果及流动阶段的划分Fig.3 Numerical simulation validation results and flow regimes division

3.2 缝网参数对试井曲线的影响

为了分析不同缝网参数对试井的响应，选择人工裂缝储容比、次生裂缝储容比、次生裂缝-人工裂缝传质系数、基质-次生裂缝传质系数、无因次人工裂缝半长等5 个参数（表2），其默认值分别取2×10-5，2×10-2，0.5，0.03，0.5。运用单因素分析方法开展评价，除分析因素变化外，其他因素均取默认值。

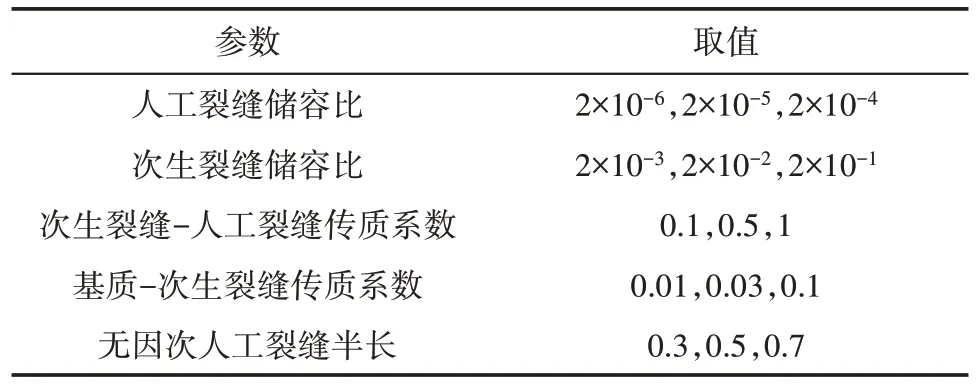
表2 体积压裂水平井缝网参数Table2 Parameters of fracture networks of horizontal well by stimulated reservoir volume

人工裂缝储容比 人工裂缝储容比主要影响人工裂缝线性流和次生裂缝-人工裂缝窜流阶段。人工裂缝储容比越小，人工裂缝线性流阶段时间越短，甚至消失（被井储阶段掩盖）。同时，随着人工裂缝储容比的减小，次生裂缝-人工裂缝窜流阶段时间发生得越早，且导数曲线上展现出“凹子”更深。由于人工裂缝储容比不同，人工裂缝线性流阶段结束的时间不同，因此图4 不能如图3 所示使用4条虚线将整个流动过程划分为5 个阶段，不同的绿色箭头代表不同储容比下人工裂缝线性流阶段结束的时刻，也相当于阶段划分线。

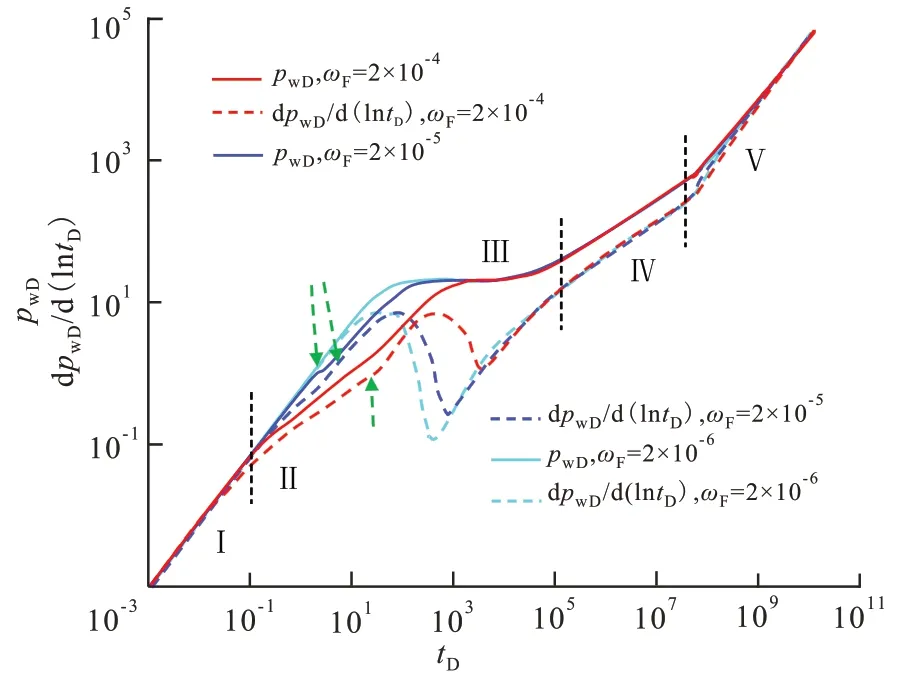
图4 人工裂缝储容比对试井曲线的影响Fig.4 Effect of artificial fracture storativity on well test curves

次生裂缝储容比 次生裂缝储容比主要影响次生裂缝-人工裂缝窜流阶段和基质线性流阶段的早期。次生裂缝储容比对次生裂缝-人工裂缝窜流阶段发生的时间没有影响，但次生裂缝储容比越小，该阶段导数曲线上展现出“凹子”越浅。同时，次生裂缝储容比越小，基质线性流阶段出现的时间越早。不同次生裂缝储容比下，次生裂缝-人工裂缝窜流阶段结束的时间不同（图5），图中箭头代表第三阶段次生裂缝-人工裂缝窜流结束的时刻。

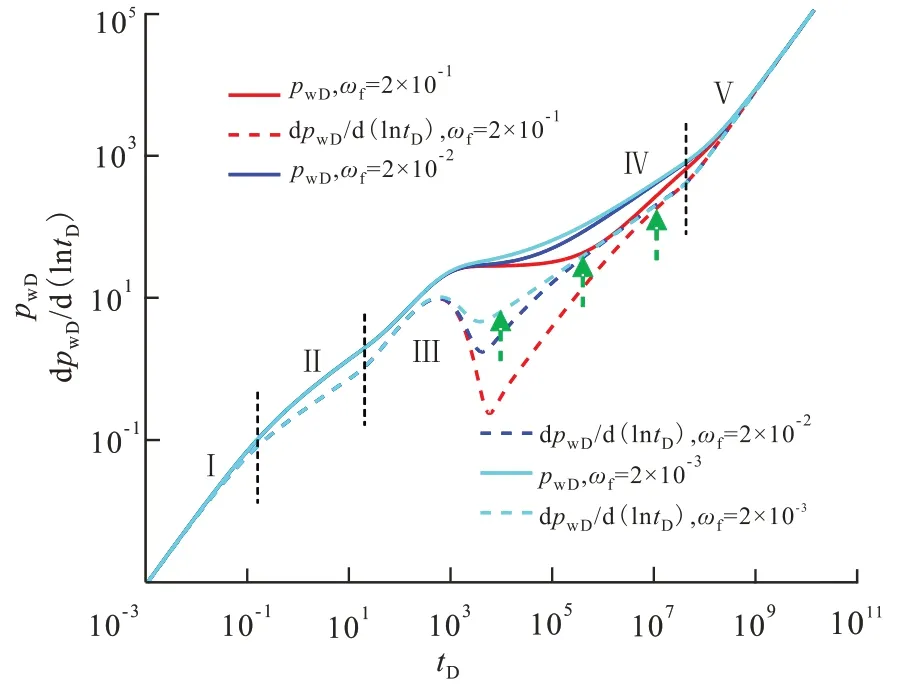
图5 次生裂缝储容比对试井曲线的影响Fig.5 Effect of secondary fracture storativity on type curves

次生裂缝-人工裂缝传质系数 次生裂缝-人工裂缝传质系数主要影响次生裂缝-人工裂缝窜流阶段和基质线性流阶段。次生裂缝-人工裂缝传质系数对次生裂缝-人工裂缝窜流阶段发生的时间有较大影响，其值越大，次生裂缝-人工裂缝窜流阶段发生得越早。同时，次生裂缝-人工裂缝传质系数对基质线性流阶段压力导数曲线的影响较小，对压力曲线的影响较大，次生裂缝-人工裂缝窜流系数越大，压力曲线越靠下（图6）。

图6 次生裂缝-人工裂缝传质系数对试井曲线的影响Fig.6 Effect of mass transfer coefficient between secondary and artificial fractures on type curves

基质-次生裂缝传质系数 如图7 所示，基质-次生裂缝传质系数主要影响次生裂缝-人工裂缝窜流阶段的晚期和基质线性流阶段。基质-次生裂缝传质系数对次生裂缝-人工裂缝窜流阶段发生的时间和“凹子”的深度都没有影响，但对“凹子”后半段的形态有影响，其值越大，导数曲线越靠下。同时，基质-次生裂缝传质系数对基质线性流阶段的影响较大，其值越大，压力曲线和导数曲线越靠下，而且边界控制流阶段发生的时间越早。不同的基质-次生裂缝传质系数下，基质线性流阶段结束的时间不同，箭头代表第四阶段基质线性流结束的时刻。

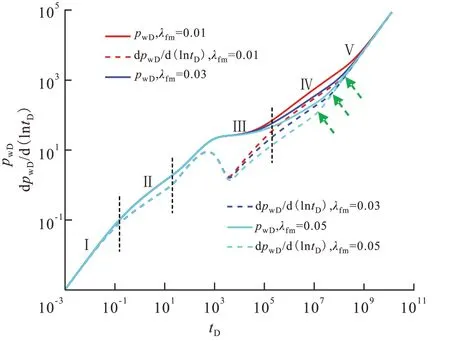
图7 基质-次生裂缝传质系数对试井曲线的影响Fig.7 Effect of mass transfer coefficient between matrix and secondary fracture on type curves

无因次人工裂缝半长 如图8 所示，无因次人工裂缝半长对试井曲线特征的影响非常大，对次生裂缝-人工裂缝窜流阶段、基质线性流阶段和边界控制流阶段都有影响。人工裂缝半长越长，压力曲线和压力导数曲线越靠下。不同的无因次裂缝半长下人工裂缝线性流阶段结束的时间不同，图中的绿色箭头代表指第二阶段人工裂缝线性流阶段结束的时刻。

图8 无因次人工裂缝半长对试井曲线的影响Fig.8 Effect of dimensionless half-length of artificial fracture on type curves

4 结论

体积压裂水平井缝网参数对试井曲线的影响较大，很多试井模型忽略次生裂缝的影响，对缝网参数的试井解释不准确。考虑体积压裂形成的复杂裂缝网络，建立体积压裂水平井试井解释正交缝网模型，通过Laplace 变换及逆变换获得了模型的解。

所建立的体积压裂水平井复杂缝网试井解释模型比平板缝模型更符合实际，而且模型方便实用，可较容易地获得其解析解；通过与数值模拟对比，验证了模型的准确性。

针对体积压裂水平井，试井过程中一般出现5个主要的流动阶段，分别是井筒储集阶段、人工裂缝线性流阶段、次生裂缝-人工裂缝窜流阶段、基质线性流阶段和边界控制流阶段。各个阶段的流动特征明显，在试井过程中能比较容易地加以鉴别。

缝网参数对试井曲线特征的影响较大，其中人工裂缝线性流阶段受人工裂缝储容比影响较大，次生裂缝-人工裂缝窜流阶段受到所有缝网参数的影响，基质线性流阶段受到除人工裂缝储容比以外的其他缝网参数的影响，边界控制流阶段受基质-次生裂缝传质系数、无因次人工裂缝半长的影响较大。

符号解释

ψ——气体拟压力，MPa2/（mPa·s）；p——压力，MPa；μ——气体黏度，mPa·s；Z——气体压缩因子；ta——拟时间，h；t——时间，h；μgi——储层原始压力下的气体黏度，mPa·s；下标i——储层原始压力条件下；ctmi——储层原始压力下的基质综合压缩系数，MPa-1；ctm——储层基质综合压缩系数，MPa-1；tD——无因次时间；下标D——无因次；KF——人工裂缝渗透率，mD；ϕm——储层基质的孔隙度，f；ϕf——次生裂缝的孔隙度，f；ϕF——人工裂缝的孔隙度，f；下标m，f，F——基质、次生裂缝、人工裂缝；ctf——次生裂缝综合压缩系数，MPa-1；ctF——人工裂缝综合压缩系数，MPa-1；Acw——水平井所在的横截面积，Acw=H⋅Xe，m2；H——储层厚度，m；Xe——水平井长度，m；pD——无因次压力；ψi——初始时刻的气体拟压力，MPa2/（mPa·s）；qsc——地面标况下的日产气量，m3/d；T——温度，K；ωm——基质储容比；ωf——次生裂缝储容比；ωF——人工裂缝储容比；λfm——基质与次生裂缝间的传质系数；Km——储层基质渗透率，mD；Lf——次生裂缝间距，m；λFf——人工裂缝与次生裂缝间的传质系数；LF——人工裂缝间距，m；Kf——次生裂缝渗透率，mD；x,y,z——x，y和z方向，m；xD,yD,zD——x，y和z方向无因次长度；ψm——基质拟压力，MPa2/（mPa·s）；ϕmi——储层原始压力下基质的孔隙度，f；——基质的内边界处（即基质-次生裂缝连接处）的拟压力，MPa2/（mPa·s）；ψf——次生裂缝拟压力，MPa2/（mPa·s）——基质外边界（即基质块中心部分）的拟压力偏导数，MPa2/（mPa·s·m）；qmf——次生裂缝与基质间的窜流，m3/s；qfF——次生裂缝与人工裂缝间的窜流，m3/s；ϕfi——储层原始压力下次生裂缝的孔隙度，f；ctfi——储层原始压力下次生裂缝的综合压缩系数，MPa-1；——基质内边界处（即基质-次生裂缝连接处）的拟压力偏导数，MPa2/（mPa·s·m）；σ——形状因子，1/m2；ψF——人工裂缝拟压力，MPa2/（mPa·s）；——次生裂缝内边界（即次生缝-人工裂缝连接处）的拟压力，MPa2/（mPa·s）；——次生裂缝的外边界（即次生裂缝端部）的拟压力的偏导数，MPa2/（mPa·s·m）；ϕFi——储层原始压力下的人工裂缝的孔隙度，f；ctFi——储层原始压力下人工裂缝的综合压缩系数，MPa-1；——人工裂缝的外边界（即人工裂缝端部）的拟压力偏导数，MPa2/（mPa·s·m）；——人工裂缝内边界处（即人工裂缝对射孔部位）的拟压力偏导数，MPa2/（mPa·s·m）；q——产量，m3/d；B——体积系数，m3/m3；pmD——基质的无因次拟压力；——基质初始时刻的无因次拟压力；——基质外边界处（即基质块中心部位）的无因次拟压力偏导数；——基质外边界处的无因次拟压力；pfD——次生裂缝的无因次拟压力；pFD——人工裂缝的无因次拟压力；——基质外边界处（即基质-次生裂缝连接处）的无因次拟压力导数；——次生裂缝初始时刻的无因次拟压力；——次生裂缝外边界（即次生裂缝端部）的无因次拟压力偏导数；——次生裂缝在外边界处（即次生裂缝-人工缝连接处）的无因次拟压力；——次生裂缝在外边界处（即次生裂缝-人工裂缝连接处）的无因次拟压力偏导数；——人工裂缝初始时刻的无因次拟压力；——人工裂缝内边界（即人工裂缝射孔部位）的无因次拟压力偏导数；——人工裂缝外边界（即人工裂缝端部）的无因次拟压力偏导数；——Laplace空间下无因次井底流压；s——Laplace 变量；yFD——人工裂缝在y方向的无因次长度；——Laplace 空间下的无因次产量解；sc——无因次表皮系数；——Laplace 空间下考虑井储考虑和表皮效应的井底无因次拟压力解。