基于新型集成学习算法的基岩潜山油藏储层裂缝开度预测算法

孙致学，姜宝胜，肖 康，李吉康

（1.中国石油大学（华东）石油工程学院，山东青岛 266580；2.非常规油气开发教育部重点实验室中国石油大学（华东），山东青岛 266580；3.中国石油勘探开发研究院非洲研究所，北京 100083）

近年来，全球已在30余个盆地发现了基岩油气资源，基岩油气藏成为重要的勘探开发阵地。相对于常规沉积岩油气储层，基岩储层中天然裂缝类型、产状、特征参数的精准评价更加重要。由于该类油气藏基岩致密、孔渗性极低，天然裂缝系统不仅控制了有效储层发育程度和油气储量规模，同时也是油气开采过程中的重要运移通道。裂缝开度是评价基岩油气藏储层质量的重要参数。相对于裂缝密度，裂缝开度对储层有效渗透率的贡献更为显著，也是影响其产能的主控因素之一［1-3］。目前储层天然裂缝开度预测方法主要分为2 大类：一类是直接观察法，包括岩心观测、露头识别、电镜观测等；另一类是间接观察法，包括成像测井、数值模拟、经验公式、动态资料分析等。其中露头识别法是获得裂缝开度最直接的途径［4］，但地表风化作用使裂缝充填特征发生显著变化，影响测量结果，同时露头区可能遭受后期的改造或掩埋，使得典型裂缝发育的露头不容易获得。岩心中包含着最为直观、详实的裂缝信息，但取心资料往往少且不连续，同时机械应力对岩心的破坏影响天然裂缝开度的测量。随着断层扫描机、阴极射线发光、核磁共振、三维激光扫描技术的发展，裂缝开度表征朝更微观、更立体和更精细的方向发展［5-6］。但由于仪器探测能力的限制，无法系统、大规模表征天然裂缝开度。成像测井具有高分辨率且连续测量的特点，能够直观地反映裂缝信息，但由于测量成本高，导致获得的数据非常有限。通过室内数值模拟装置进行裂缝开度模拟分析，测量相对误差较小，但装备适用范围有限，实验参数难以获得，无法真实还原地层条件。进行应力场有限元数值模拟需考虑地质体的岩石物理特征，所需参数较多，难以准确获取。该方法可以在一定程度上预测裂缝分布，但由于模型并不能反映实际地层情况，导致误差较大［7-8］。依据渗流力学原理，利用泥浆漏失数据建立裂缝泥浆漏失数学模型，根据钻井资料进行裂缝开度计算也是当下研究的热点。但该方法受漏失数据的限制，适用范围有限。对大多数油田而言，现有资料中除了少量取心资料外，其余几乎是常规测井资料，因此如何利用常规测井信息建立裂缝的测井响应机理模型，进而计算天然裂缝开度，是不得不面对的实际问题。目前应用测井数据解释天然裂缝仍停留在定性分析水平上［9-10］。主要是由于传感器捕获的实时测井数据具有高维、非线性和高噪性的特点，难以建立与裂缝开度之间的量化关系。机器学习对于解决非线性问题具有先天优势，而集成学习是机器学习领域的研究热点［11］，相较于单一机器学习算法，集成学习算法具有更高的精度和更显著的泛化性能。

图1 中非乍得某基岩潜山岩心裂缝照片Fig.1 Photos of fractured core samples from bedrock buried hill in Chad，Central Africa

1 样本集构建

研究区位于B 盆地中非乍得西南部、中非剪切带中段北侧，大量岩心和井壁取心分析资料揭示B盆地基岩潜山岩性分为变质岩和岩浆岩2 大类13个亚类30多种岩石类型，主要由花岗岩、正长岩、闪长岩和二长岩等岩浆岩及混合花岗岩和片麻岩类等正变质岩构成［12］。通过对该潜山15口取心井（含新完钻井）岩心裂缝形态、规模及典型特征进行观察及描述，发现研究区油气运移通道包括构造裂缝、网状缝、张剪缝及沿缝溶蚀孔洞，以张剪缝为主（图1）。

1.1 学习样本特征

准确且全面的裂缝数据样本是实现模型训练的基础。所用数据集包括测井数据（表1）及相应裂缝开度值，共2 140 组，由基岩潜山油藏岩心描述、关键井成像测井、岩矿薄片鉴定等数据组成。由裂缝开度分布（图2）可知，样本集中裂缝开度最小值为0.011 mm，最大值为0.544 mm，平均值为0.183 mm，标准差为0.087 mm，裂缝开度主要集中在0.126～0.258 mm。

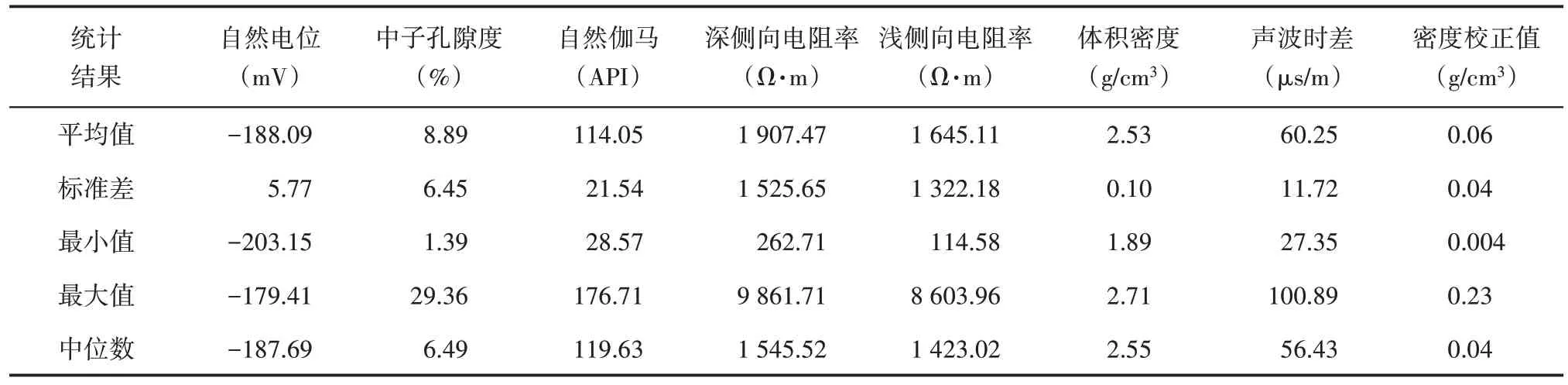
表1 测井数据统计结果Table1 Statistics of well logging parameters

图2 裂缝开度分布Fig.2 Fracture aperture distribution

1.2 Z-score标准化处理

在进行裂缝预测前，需将学习样本进行Z-score标准化处理，即将其转换为均值为0、方差为1 的分布，其表达式为：

如果一个特征的方差比其余特征的方差大许多个数量级，那么该特征将会主导整个目标函数，使得模型不能从其余特征学习到数据的特征。相对于min-max 归一化方法，该方法不仅能够去除量纲，还能够均衡考虑所有维度的变量。

1.3 K均值聚类算法进行样本去噪

样本数据由于测量仪器及人为因素的干扰，不可避免的引入噪声。为此采取利用K均值聚类算法进行数据过滤的思路，以去除冗余，提高学习样本质量。

K均值聚类算法是基于距离的聚类算法，将距离作为相似性的评价指标，即对象之间的距离越近，相似度越大。而异常点通常距离中心点较远，检测异常点，从而进行样本过滤［13］。假设输入的样本向量集合为：

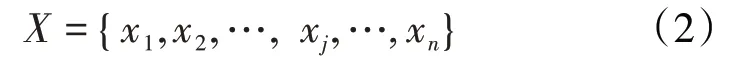
K均值聚类算法具体步骤包括：①从输入的样本向量集合中随机选取1 个向量作为第1 个簇中心点，簇中心集合记为center。②对于满足条件的任意向量，计算与最近簇中心的距离。③计算每个向量被选为簇中心的概率，其表达式为：

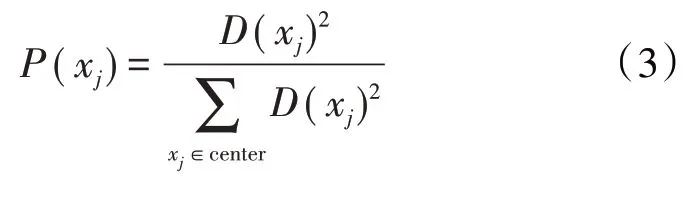
④P(xj)最大时对应的向量就是新的簇中心，若新的簇中心改变则重复步骤②—③直到目标函数收敛，聚类结束。

K的取值对聚类算法的效果具有极大影响。若K取值过小，将导致数据粗化，在剔除异常点的同时会误判正常数据，造成有效样本丢失；若K取值过大，将致使聚类结果无法有效收敛，计算时间过长，导致无法有效筛选异常数据。为此采用手肘法来确定K值。手肘法的核心指标是误差平方和，其表达式为：

该方法的核心思想是随着K值的增加，样本数据划分更加精细，各个簇的聚合度逐渐提高，误差平方和逐渐减小。当K值小于真实聚类数时，K值增加会显著增强各个簇的聚合度，误差平方和下降幅度变大。当K值接近真实聚类数时，提高K值各个簇的聚合度变小，误差平方和变化幅度骤减（图3）。

由图3 可知，当K取值为5，即当聚类数为5 簇时，K均值聚类算法性能最优，过滤异常值能力最强，因此本文聚类数取5。同时计算距离时容易受较大数据的影响而忽略取值较小的数据，需在聚类前进行Z-score 标准化处理。然后通过K均值聚类算法对样本数据进行去噪，找出异常点72组。将异常点剔除，其余2 068 组样本数据用于后续算法的训练与测试。

图3 误差平方和、计算时间与聚类数的关系Fig.3 Relationship among sum of squared errors，calculation time and cluster number

2 预测算法建立

作为机器学习的最新技术，集成学习在智能计算和机器学习领域引起了广泛关注。集成学习不是一种特定的模型而是一种思想，通过结合较简单的基础模型来构建强化模型。本文引入集成学习技术，将2种不同的基础模型结合起来，生成一个更好的模型来预测裂缝开度。

2.1 支持向量回归算法

鉴于地质认识及资料丰度的不确定性，以及特征之间具有复杂的非线性关系，应用传统回归模型不能较好地进行裂缝开度预测。而支持向量回归算法可通过核函数将样本数据映射到高维空间，解决非线性问题，同时该算法具有良好的稳定性和泛化能力［14］。支持向量回归算法可形式化为：

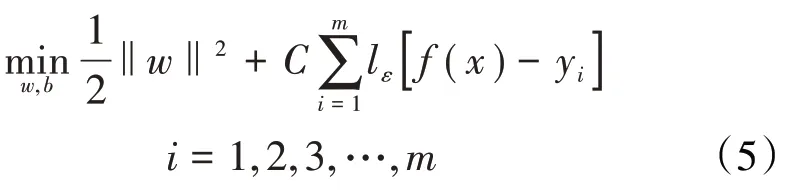
引入松弛变量ξi和，可将（5）式写为：

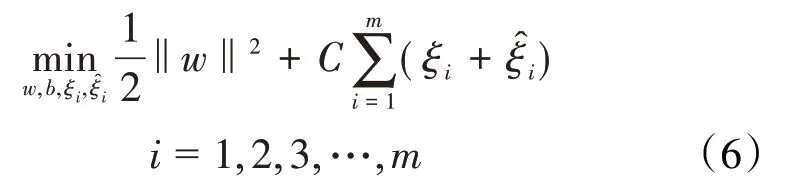
引入拉格朗日算子ui≥0,≥0,ai≥0,≥0，其拉格朗日函数表达式为：

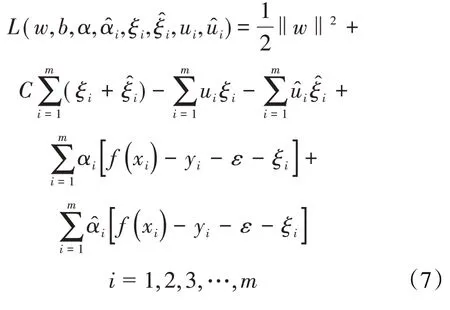
其中：

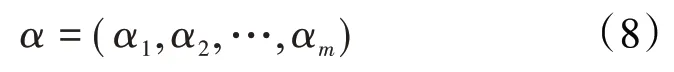
根据wolf 对偶的定义，在KKT 条件下得到拉格朗日对偶形式为：

支持向量回归算法函数表达式为：

对于非线性问题，可通过非线性变换转化为某个高维空间中的线性问题，即用核函数k(x,xi)替换可以实现非线性函数拟合，能较好处理非线性以及高维数的问题，可表示为：

2.2 XGBoost回归算法

XGBoost 是由一系列回归树组成的强大的预测模型。其核心思想是不断添加回归树，通过生成新树来拟合前一棵树的残差。当训练完成得到N棵回归树时，将每棵树对应的分数加起来就是该样本的预测值［15］，其表达式为：

XGBoost目标函数为：

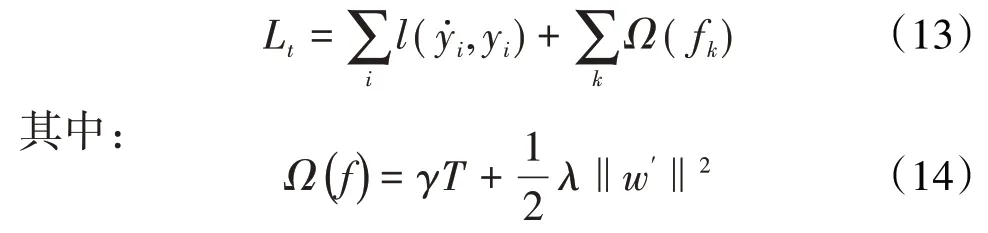
为避免算法拟合过程中的过拟合，算法不能同时训练所有回归树，因此利用固定训练好的回归树，依次添加一棵新树来解决，假设步骤t的预测值用表示，（12）式可以写为：

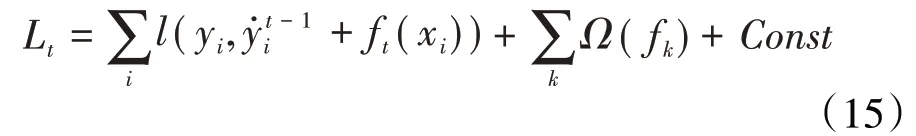
将其进行二阶泰勒展开为：

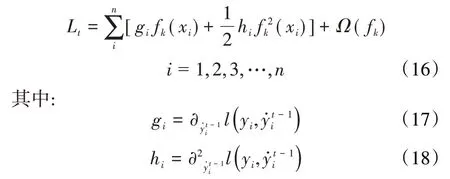
则（15）式可以改写为：

2.3 基于岭回归的集成学习算法

本文所提的裂缝开度预测集成算法以XGBoost回归算法和支持向量回归算法为基础模型。每个基础模型均接收输入数据，并给出独立的裂缝开度预测结果，这些预测结果均作为元特征，被馈送到元学习器中（本文的元学习器采用岭回归算法），并给出最终的裂缝开度预测结果（图4）。

图4 基于岭回归的集成学习算法Fig.4 Ensemble learning algorithm based on ridge regression

该算法为基础学习器δg=1,2（g=1 为支持向量回归，g=2 为XGBoost 回归）对于H折交叉验证中的每一个待预测的训练样本集合DH都有与之对应的训练集预测结果集合ZHg。这样的循环过程完毕后，对于每个基础学习器而言，都有H对同质基础学习器训练集预测值，将其整合为D2g。再将所有基础学习器D2g整合作为元特征定义为D2。将D2馈送到岭回归算法得到加权结果即为最终预测开度值。基于岭回归的集成学习算法的最终表达式为：

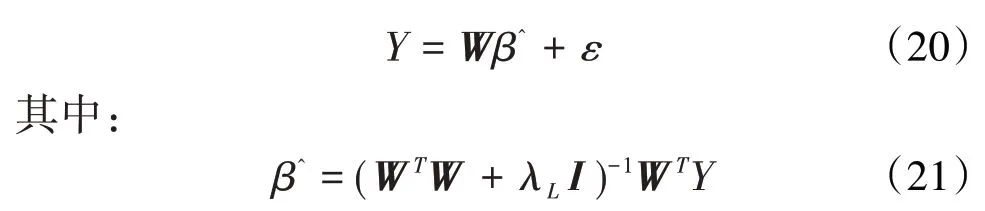
在此基础上，经K均值聚类算法去噪后，应用基于岭回归的集成学习算法进行裂缝开度预测，笔者将其定义为新型集成学习算法。

3 预测算法应用

3.1 模型参数优化求解

机器学习算法参数的选择直接决定了算法的性能。网格搜索法是当前应用最为广泛的参数优化算法。但该方法依靠穷举所有参数进行优化，计算成本过于庞大，同时对于连续数据需要等间取样，不一定能取得全局最优。故采用随机搜索进行参数优化，该方法主要原理是从指定的分布中采样固定数量的参数设置。与网格搜索法相比，该方法在保障准确度的同时，显著减少计算时间。

根据测试集上模型的均方根误差值来判断基础模型最佳超参数。其中支持向量回归算法的主要超参数为惩罚系数，XGBoost 回归算法的主要超参数为最大深度，其超参数随机优化调参过程如图5 所示。在搜索的过程中，超参数快速收敛，并找出最优值。支持向量回归算法的惩罚系数搜索范围为0～20，最优值为0.147，对应均方根误差为0.113；XGBoost 回归算法的最大深度搜索范围为0～18，最优值为13，对应均方根误差为0.076。

3.2 模型应用评价分析

确定好模型参数之后，随机选取80%经过Zscore 标准化处理后的样本数据作为训练集共1 712组，20%的样本数据作为测试集共428 组来验证模型效果。以均方根误差（RMSE）和真实裂缝开度值与预测裂缝开度值间相关系数（R2）作为评价标准。将测试集分别代入训练好的支持向量回归算法、XGBoost 回归算法及基于岭回归的集成学习算法中，计算测试集中真实裂缝开度与预测裂缝开度间相关系数（图6）。

图5 随机搜索优化调参过程Fig.5 Parameter adjustment optimization process based on random search

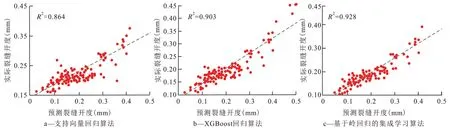
图6 预测裂缝开度与真实裂缝开度交会图Fig.6 Cross plot of measured and predicted apertures

由图6 可以看出，3 种算法中，基于岭回归的集成学习算法的R2最高，达0.928。同时为探究K均值聚类降噪效果，将样本数据馈送于基于岭回归的集成学习算法中进行训练和测试，并与先前计算结果进行综合对比（表2），发现4 组方法中K均值-基于岭回归的集成学习算法的RMSE 最小，R2最大。即该算法的预测裂缝开度值与真实裂缝开度值之间的偏差最小，支持向量回归算法的RMSE 最大，R2最小。K均值聚类算法能够对学习样本进行有效降噪，去除冗余，提高了学习样本的质量。

表2 各算法预测效果对比Table2 Comprehensive comparison results of prediction effects in various algorithms

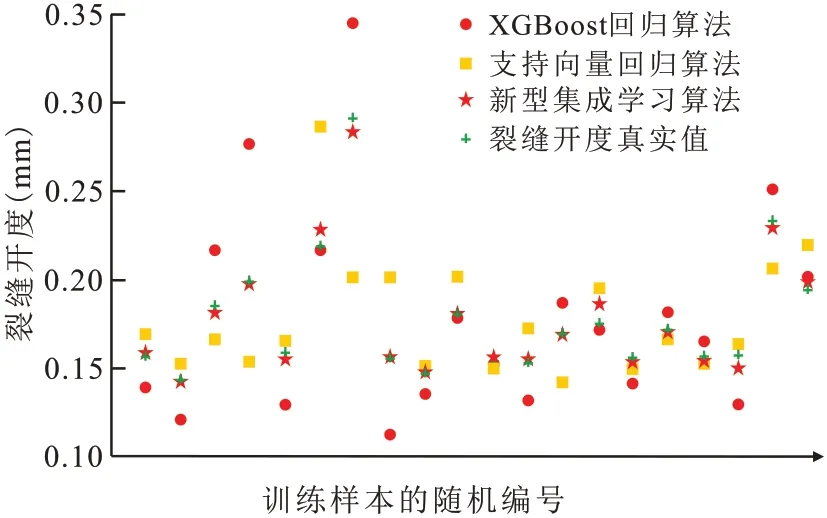
图7 样本观测值Fig.7 Sample observation values

为进一步综合分析该算法的预测效果，将部分样本真实值及各算法预测值进行可视化研究。从图7 可以明显看出，支持向量回归算法和XGBoost回归算法预测值整体在真实值上下波动，支持向量回归算法总体变化平稳，但对裂缝开度突变值检测不明显。XGBoost 回归算法对数据敏感，部分数值波动较大。新型集成学习算法的计算结果紧密围绕真实裂缝开度值波动，很好地结合了基础算法的优点，平衡了基础算法的缺点，预测精度明显提升。

4 结论

利用测井数据及其对应裂缝开度值，提出基于新型集成学习的基岩潜山油藏储层裂缝开度预测算法。该算法先通过K均值将学习样本进行聚类、降噪来提升学习样本质量；以支持向量回归算法和XGBoost 回归算法为基础模型，并利用随机搜索进行基础模型参数优化。然后利用岭回归算法对优化好的基础模型进行集成组合。所提出的新型集成学习算法建立的裂缝开度预测模型弥补了单一回归算法不稳定的特点，提升了预测精度，能够充分挖掘测井数据中蕴含的地质信息，为裂缝开度定量预测提供了新的思路。同时该方法可实现自动、快速优化调参，具有广泛的适用性。

符号解释

x'——标准化处理后的样本数据；x——样本数据；μ——样本均值；δ——样本方差；K——聚类数，簇；X——样本向量集合；j——样本序号；n——样本向量总数；center——簇中心集合；P(xj)——簇中心概率；D(xj)2——最近簇中心的距离；SSE——误差平方和；i——样本列号；p——Ci中的样本点；Ci——第i个簇；mi——Ci中所有样本的均值；w——法向量；b——位移项；C——惩罚系数；m——样本数量；lε——不敏感损失函数；ε——软间隔带；f(x)——支持向量回归算法函数；yi——开度实际值；ξi和松弛变量；和——在第i数据下不同的拉格朗日算子；α——拉格朗日算子αi的合集；拉格朗日算子的合集；——在第j数据下不同的拉格朗日算子；xi和xj——输入的第i和第j个数据；k(x,xi)——核函数开度预测值；N——回归树的总数，个；fk——第k棵回归树算法；Lt——步骤t下的目标函数；t——步骤序号；——预测开度值与真实开度值的差；Ω(f)——惩罚项；γ——回归树分割的难度系数；T——回归树叶子节点个数，个；λ——L2正则系数；w′——回归树叶子节点权重——步骤t的预测值；Const——常数；gi——损失函数一阶导数；hi——损失函数二阶导数；Ij——第j个叶子的样本集合；δg=1,2——基础学习器；H——交叉验证折数；DH——H折交叉验证中的每一个待预测的训练样本集合；ZHg——与DH对应的训练集预测结果集合；D2g——H对同质基础学习器训练集预测值；D2——元特征；Y——预测的最终开度值；W——元特征数据矩阵；β^——岭回归估计值；λL——岭参数；I——单位矩阵。