含未知参数的一维人群动态系统的自适应边界控制

秦 伟,CONTRERAS Sergio,崔宝同

(1.江南大学物联网与工程学院,江苏无锡 214122;2.内华达大学拉斯维加斯分校电气与计算机工程系,美国拉斯维加斯89154)

1 引言

随着城市规模的不断扩大,越来越多的人口涌入城市.城市中一些主要的生活场所如地铁站,大型商场,学校等会经常出现人群的聚集.如何对这样大规模的人群进行管理,防止拥挤踩踏事件的发生,以保证人们的人身安全,获得良好的舒适度体验是个值得研究的课题.1993年在伦敦举行的人群安全工程会议[1]就指出了人群管理的重要性,引起了众多学者的关注.

目前,对人群动态管理的研究主要集中在两个层面.一种是将行人作为离散的个体来研究,把每个人作为研究对象,建立离散数学模型[2–3],通过计算机仿真来模拟行人行进路线的选择.这种研究方式能真实的模拟现实中的人群动态,但是当行人数量庞大时,再用这种方法去建模仿真将变得非常困难.另一种方式是借助流体动力学的知识,将大规模的行人看作一个整体来研究.用局部平均人群密度、平均人群移动速度来建立连续体模型描述人群动态.

基于3个假设,Hughes[4]建立了一阶行人交通连续体模型.Jiang等[5]构建了一个包含二维欧拉方程的高阶人群动态大尺度模型.Xiong等[6]将基于多智能体的微观人群动态模型与基于连续体的大尺度人群动态模型相结合,提出了一种用于人群仿真的混合建模方法.Jiang等[7]构建了描述双向行人交通的高阶人群动态连续体模型.以上研究主要针对各类人群动态进行仿真建模,而对人群动态控制策略的研究相对较少,Wadoo等[8]为一类一维人群动态模型设计了扩散、对流、对流–扩散3种状态反馈控制律.Shende等[9]对拥堵状态下的走廊人群动态进行优化控制.Qin等[10]为一类由扩散模型描述行人移动速度与密度关系的人群动态模型设计了状态反馈控制律,并解决了控制饱和问题.秦等[11]为扰动状态下的人群动态系统设计了Robin,Neumann,Dirichlet 3种边界控制律来保证人群向特定的方向平稳移动.

文献[11]对人群动态系统的研究是在假设系统扩散系数及边界条件中的相关参数已知的情况下完成的,但由于人群动态的复杂性,试验所得的人群动态的扩散系数及边界条件系数难免存在误差,必然会影响控制器的作用效果.自适应控制方法通过寻找未知参数的动态调节律来补偿未知性，是解决具有不确定性或未知性系统控制问题的主要方法.因此,本文借助自适应控制工具[12–13],在假设扩散系数及边界条件系数未知的情况下,设计自适应边界控制律来对人群动态进行管理,进一步完善了文献[11]的研究成果.

本文组织结构如下:首先,介绍描述系统动态的连续体模型.然后设计自适应边界控制律,借助Lyapunov稳定性判据给出详细的指数稳定证明.最后用一实例来验证自适应边界控制律的有效性.

为了书写方便,本文采用如下记号:

2 系统模型

基于数量守恒定律,建立描述存在扰动的一维人群动态模型如下(详细建模过程见文献[11]):

其中:x ∈[0,L]表示空间位置,区间长度L为正常数;t ∈[0,∞)表示时间;ρ(x,t)∈H2表示人群密度,H2(0,L)为Sobolev空间;v(x,t)表示人群移动速度;q(x,t)表示人群流量,且人群流量、速度与密度之间有如下关系:

vf表示自由移动速度,也就是当人群密度为0时,行人可以达到的最大移动速度,取值已知(1.4 m/s);ρm表示人群的最大密度,取值已知(5人/m2);D >0 表示扩散系数,一般由试验所得,但存在较大误差.µ为常数,表示扰动系数,取值可正可负.初始条件为

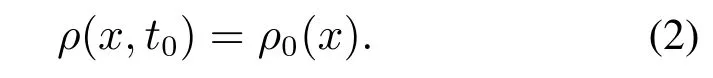
边界条件为

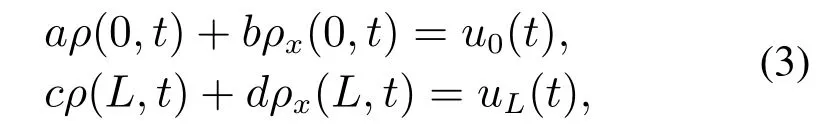
其中:u0(t)与uL(t)分别为0边界与L边界的控制输入;a,b,c,d均为常数,但由于边界处人群动态的复杂性，取值往往难以确定.接下来,在假设扩散系数D及边界条件中a,b,c,d取值未知的情况下,借助自适应边界控制工具,来控制人群动态系统的稳定性.

3 自适应边界控制

为了证明主要结论,先引入以下几个引理.

引理1(Poincar´e不等式)[14]对任意的ρ(x,t)∈C1[0,L],以下不等式成立:

引理2[15]令α<0.如果ρ(0,t)∈L2(0,∞),则

借助引理2,推得以下3个引理:

引理3令α<0.如果ρ(L,t)∈L2(0,∞),则

引理4令α<0.如果ρ(0,t)∈L3(0,∞),则

引理5令α<0.如果ρ(L,t)∈L3(0,∞),则

定理1假设人群动态系统(1)–(3)的扩散系数D与边界条件中的系数a,b,c,d是未知的.当<0时,人群动态系统(1)–(3)在以下控制律的作用下是指数稳定的,

其中ηi(t)(i=1,2,3,4)对任意的t≥0都是有界的,且满足

γi(i=1,2,3,4)为正常数.

证构造Lyapunov泛函

并对时间t求导得

由分部积分法得

将边界条件

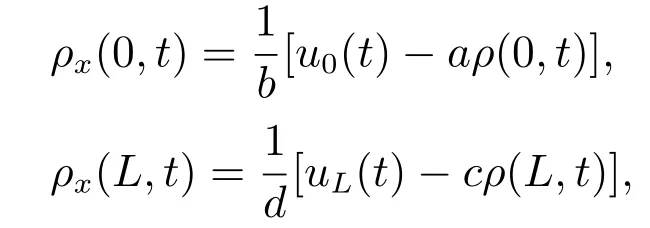
代入式(6)得

由引理1得

将控制律(4)代入上式得

接下来,引入一非负的能量函数E(t):

对时间t求导得

将式(5)与式(8)代入式(9)得

由Gronwall不等式得

借助引理2–5可以得到

因此,人群动态系统(1)–(3)在控制律(4)的作用下指数稳定. 证毕.

4 数值仿真

本节通过一个实例来验证自适应边界控制律(4)的有效性,仿真方法为有限体积法[16].假设人群疏散系统(1)–(3)初始密度满足高斯分布

其中:G为最大密度值;δ为高斯分布的中心.数值仿真主要参数取值为:G=5,δ=2,L=4,ρm=5,vf=1.4,a=1,b=1,c=1,d=1,γ1=1,γ2=1,γ3=2,γ4=2.

下面,将对未加控制的人群动态系统,自适应边界控制下的人群动态系统,以及文[11]中设计的Robin边界控制下的人群动态系统分别在扩散系数D=1,D=0.1两种状态下的人群密度演化情况进行对比.

图1为扩散系数D=1时,未加控制的人群动态系统三维密度演化图.在未对人群动态系统施加任何控制的情况下,由于扩散项ρxx与平流项ρx的作用,人群密度仍缓慢的扩散并向出口x=4移动,经过足够长的时间,逐渐变为0.为了更明显的演示密度变化,选取中点x=2与出口x=4两点做密度演化图,如图2所示.

图1 当D=1时,未加控制的人群动态系统三维密度演化图Fig.1 3D density response of uncontrolled crowd dynamic systems when D=1

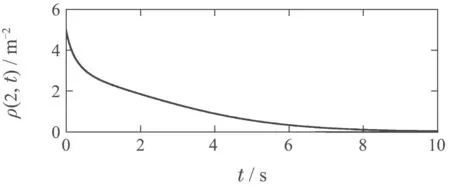
图2 当D=1时,未加控制的人群动态系统在x=2,4两点密度演化图Fig.2 The density response of uncontrolled crowd dynamic systems at point x=2,4 when D=1

由图2可以看出,中点x=2的密度大约在9 s处变为0,出口x=4的密度在10 s处仍未变为0,说明疏散过程仍未结束.图3与图4分别为扩散系数D=1时,自适应边界控制下的人群动态系统三维密度演化图与x=2,4两点处的密度演化图.由图4可知,中点x=2的密度大约在3.8 s处变为0,出口x=4的密度大约在5.2 s处变为0,完成疏散过程.对比图1与图2可以清楚的看到自适应边界控制律提高了疏散效率.

图3 当D=1时,自适应边界控制下的人群动态系统三维密度演化图Fig.3 3D density response of crowd dynamic systems with adaptive boundary control when D=1

图4 当D=1时,自适应边界控制下的人群动态系统在x=2,4两点密度演化图Fig.4 The density response of crowd dynamic systems with adaptive boundary control at point x=2,4 when D=1

图5 为扩散系数D=1 时,文献[11]中Robin边界控制律作用下的人群动态系统在x=2,4两点处的密度演化图.由图5可知,中点x=2的密度大约在5.8 s处变为0,出口x=4 的密度大约在7.2 s处变为0.对比图4与图5可知,本文设计的自适应边界控制律要优于文献[11]中设计的Robin边界控制律.

图5 当D=1时,文献[11]中Robin边界控制律作用下的人群动态系统在x=2,4两点处的密度演化图Fig.5 The density response of crowd dynamic systems at point x=2,4 with Robin boundary control in the paper [11]when D=1

接下来,对扩散系数D=0.1时的情况进行对比.当扩散系数D=0.1时,未加控制的人群动态系统三维密度演化过程如图6所示.减少了扩散项的影响,平流项的作用更加明显,人群更快的向出口移动.同样选取中点x=2与出口x=4两点做密度演化图,如图7所示.中点x=2 的密度大约在5 s 左右变为0,出口x=4的密度大约在8.2 s左右变为0,达到的最大密度为2左右.对比图2 可知,由于扩散作用影响的减少,人群更快速的向出口方向移动,所以当扩散系数减小时,未加控制的人群动态系统在更短的时间内完成了疏散过程.

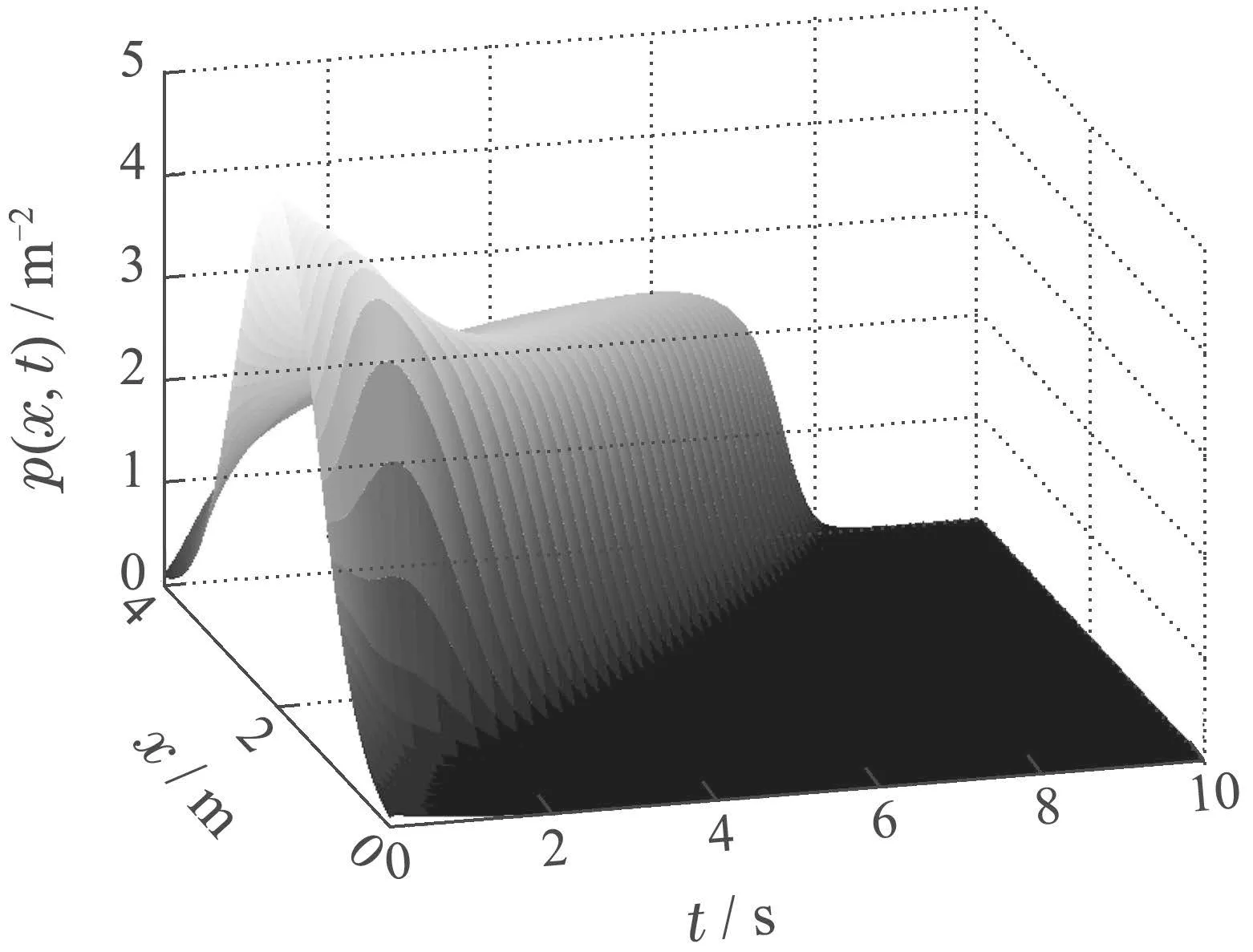
图6 当D=0.1时,未加控制的人群动态系统三维密度演化图Fig.6 3D density response of uncontrolled crowd dynamic systems when D=0.1

图7 当D=0.1时,未加控制的人群动态系统在x=2,4两点密度演化图Fig.7 The density response of uncontrolled crowd dynamic systems at point x=2,4 when D=0.1

图8与图9分别为扩散系数D=0.1时,自适应边界控制下的人群动态系统三维密度演化图与x=2,4两点的密度演化图.

图8 当D=0.1时,自适应边界控制下的人群动态系统三维密度演化图Fig.8 3D density response of crowd dynamic systems with adaptive boundary control when D=0.1

图9 当D=0.1时,自适应边界控制下的人群动态系统在x=2,4两点密度演化图Fig.9 The density response of crowd dynamic systems with adaptive boundary control at point x=2,4 when D=0.1

由图8可以看到,中点x=2的密度在2.0 s左右变为0,出口x=4的密度在3.9 s左右变为0,且达到的最大密度为0.9左右.对比图7可知,在自适应边界控制律的作用下,人群动态系统不仅在更短的时间内完成了疏散,并且出口处的最大密度有很大幅度的减小.最大密度的减小减少了出现拥堵、踩踏等事故的几率,使行人得到更加良好的舒适度体验.

图10为扩散系数D=0.1时,在文献[11]中Robin边界控制律作用下的人群动态系统在x=2,4两点密度演化图.中点x=2的密度在4.6 s左右变为0,出口x=4的密度在7.9 s左右变为0.对比图7未加控制的人群动态系统密度演化,文献[11]中Robin边界控制律在扩散系数D=0.1时,作用效果不明显,而本文设计的自适应边界控制律在扩散系数发生变化时，依然能够起到很好的控制疏散效果.综合以上对比,可以看到自适应边界控制律的有效性.

图10 当D=0.1时,文献[11]中Robin边界控制律作用下的人群动态系统在x=2,4两点密度演化图Fig.10 The density response of crowd dynamic systems at point x=2,4 with Robin boundary control in the paper [11]when D=0.1

5 结论

本文借助自适应边界控制工具,针对一类存在扰动的一维人群动态系统,在扩散系数及边界条件某些系数不确定的情况下,完成了系统的稳定性控制,以保证人群能按照设定的方向平稳疏散.发挥了自适应控制的优点,减少了实际应用中扩散系数等不确定性因素的影响,更便于实际应用.研究成果可以应用到生活中单入口–单出口场所的人群动态管理.