基于分子动力学的沥青自愈合行为研究

汤 文，王基双，吕悦晶

(武汉科技大学汽车与交通工程学院，湖北 武汉 430065)

已有研究证实，沥青具有一定的自愈合能力，即其在使用期间可对自身损伤进行自我修复[1]。早期沥青自愈合行为研究主要借助基于动态剪切流变仪(DSR)的动态剪切流变试验，通过分析试验过程中材料的能量耗散等指标，建立起材料损伤与自愈合的关系。Bhasin等[2]认为沥青胶结料的自愈合过程与其分子扩散密切相关，后者影响分子的随机化组合排列。显然，要进一步清晰地阐明沥青胶结料的自愈合机理，需在微观领域更深入地开展相关研究[3]。沥青的化学组成非常复杂，早期沥青分子动力学模拟一般采用沥青的平均分子结构模型，随着相关研究的不断深入以及模拟计算能力的不断提升，目前大多采用多组分模型模拟沥青的微观分子结构[4]。有鉴于此，本文采用四组分模型研究沥青内部微裂缝的自愈合过程，分析了沥青自愈合过程中其内部分子的运动规律，并计算出不同温度条件下，基质沥青、改性沥青及各自组分在自愈合过程中的扩散速度，对比了基质沥青与改性沥青的自愈合性能。

1 沥青分子结构模型的构建与验证

基于与实际沥青组成最为接近的SHRP计划中的AAA-1沥青模型[5]，参考实际沥青的组分构成[6]，利用沥青质、极性芳香分、环烷芳香分及饱和分等四组分构建基质沥青分子结构模型，该模型的分子组成[7-9]及相关参数如表1所示。

将基质沥青中12种沥青分子按照表1所列分子数目组合到1个非晶体单元中，采用蒙特卡洛(MC)方法构建基质沥青的初始分子结构模型，同时，为了分析苯乙烯-丁二烯-苯乙烯嵌段共聚物(SBS)改性剂[10]对沥青自愈合性能的影响，另外向基质沥青初始分子结构模型中加入1个线性SBS分子链构建改性沥青的初始分子结构模型。1个线性SBS分子链由中间段3个丁二烯及两端各6个苯乙烯组成(分子结构模型见图1)，其质量约占改性沥青分子结构模型总质量的4.31%。在298 K条件下，基质沥青与SBS改性沥青的初始分子结构模型均经能量最小化后采用正则系综(NVT)弛豫80 ps，然后在等温等压系综(NPT)中弛豫1000 ps，待体系能量、密度、温度等指标收敛后得到稳定的沥青分子模型。计算中采用COMPASS力场、周期边界条件、作用力截断半径为1.25 nm、时间步长为1 fs，NPT系综中压强为0.1013 MPa。

图1 SBS分子结构模型

为了验证所构建基质沥青及改性沥青分子结构模型的准确性，在不同温度下，将相应模型分别在NPT系综中继续运行1000 ps，所得基质沥青与改性沥青密度随温度的变化曲线如图2所示。由图2可见，在相同温度条件下，加入SBS分子链改性后的沥青相比基质沥青密度略有增大，尤其低温时的增量更加明显。经对比分析可知，基质沥青和改性沥青的密度与SHRP计划中 AAA-1沥青密度测定值[11]十分接近，前两者与后者在不同温度下的密度差值均小于0.07 g/cm3，表明本研究所构建的分子结构模型具有较高的精度。此外，利用图2所示实验数据可求得基质沥青与SBS改性沥青的玻璃转化温度(Tg)分别为277.85、268.28 K，这都与AAA-1沥青的相应值(约为273 K)[11]非常接近，同时注意到，SBS的掺入降低了沥青的玻璃转化温度，这有利于提高其低温性能。

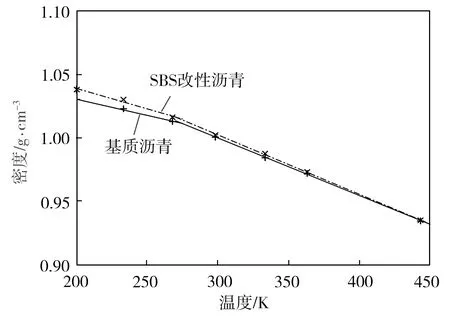
图2 沥青密度随温度的变化曲线

Fig.2 Variation of asphalt binder densities with temperatures

2 沥青的自愈合过程分析

沥青自愈合本质上是沥青分子穿过损伤界面互相靠近、互相渗透以及无序化运动的过程，了解自愈合过程中沥青分子的运动规律对认清沥青的自愈合行为非常重要。为了模拟沥青的损伤自愈合过程，在2个沥青非晶体单元之间加入宽度为1 nm的真空层，代表沥青的裂缝模型，真空层的宽度代表模型的损伤程度。沥青非晶体单元的边长约为3.8 nm，明显大于真空层宽度以保证模拟精度。图3所示为333.15 K条件下沥青裂缝初始的稳定化模型以及该模型经NVT弛豫1000 ps时的愈合模型。由图3可见，通过分子的扩散运动，初始模型中的裂缝最终愈合。

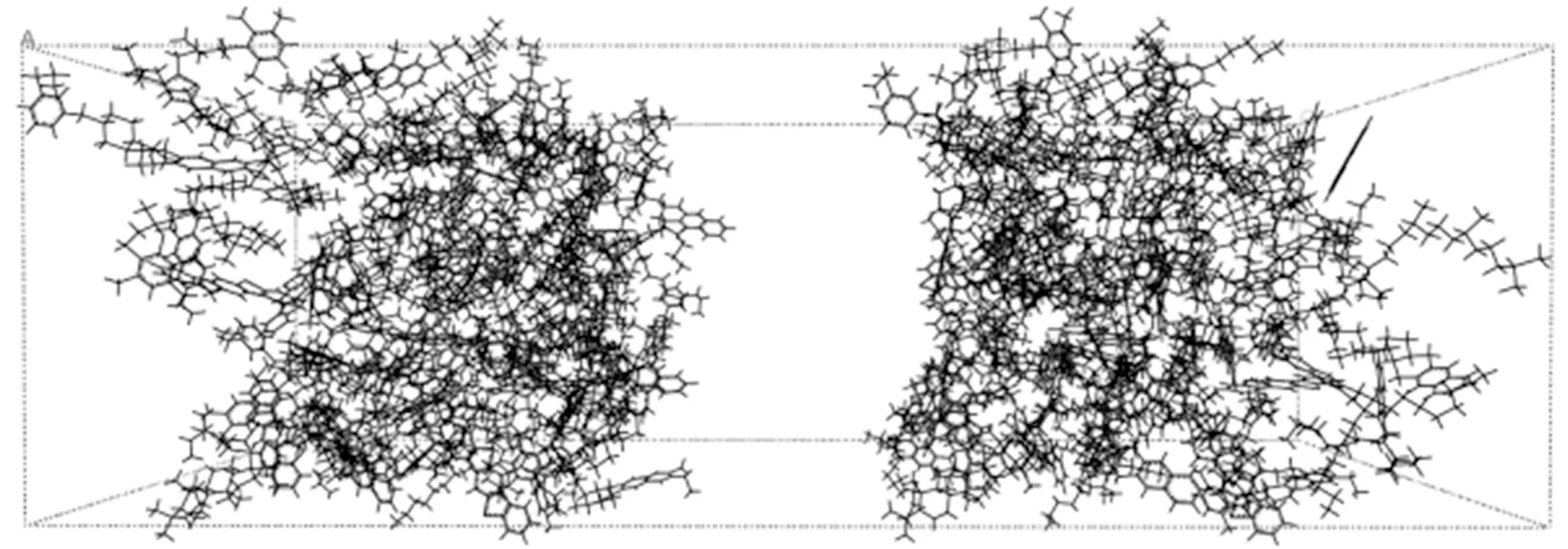
(a)初始模型

(b)愈合模型

自愈合过程中沥青分子的运动较为复杂，本研究采用粒子平均位移随时间的变化曲线描述自愈合过程中的粒子运动，相应表达式为

(1)

式中，S(t)为粒子在t时刻相对于初始时刻平均位移；N为模型中粒子总数；s(t) 和s(0)分别为粒子在t时刻及初始时刻的位置向量。

当温度为333.15 K时，沥青分子在沥青自愈合过程中的平均位移S以及S分别在裂缝深度方向(z方向)和垂直于裂缝深度方向(x方向)上的分量SZ、SX随时间的变化曲线如图4所示。由图4可见，S、SZ、SX开始均随时间的延长而逐渐增大，当达到一稳定值后基本保持不变，并且SZ较SX增幅更大，这表明裂缝两侧的沥青分子具有向对侧靠近从而填充裂缝的趋势，从而使体系的密度逐渐达到平衡密度。裂缝愈合造成的沥青模型体积收缩以z方向的收缩为主，x方向收缩量较小。此外，基于曲线的特征可将沥青自愈合过程分为三个阶段：(1)自由运动阶段。S-t曲线近似为直线，且斜率较大，在此阶段，沥青分子穿过损伤界面并互相靠近，分子碰撞较少，分子运动速度大，密度增长快；(2)互相渗透阶段。S-t曲线斜率逐渐减小，此时裂缝界面两侧的沥青分子已经靠近且互相渗透，由于体系密度增大，分子碰撞增多导致分子运动速度逐渐降低，密度增长速度也随之减小；(3)无序化运动阶段。S-t曲线近似为直线且斜率较小，沥青分子定向移动已经完成并进入无序化运动状态，密度增长缓慢。

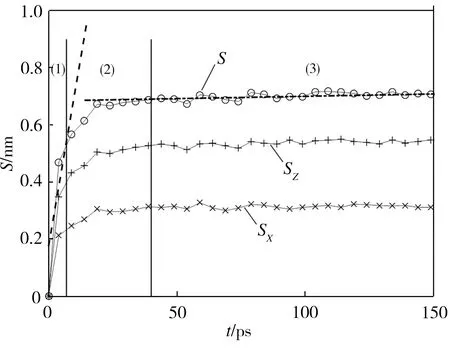
图4 沥青分子的位移曲线

3 沥青分子的扩散行为分析

沥青自愈合过程中沥青分子的移动本质上是沥青分子的扩散运动，分子扩散速度越快，自愈合效果越显著。采用分子扩散理论进一步研究沥青分子的扩散行为，任一个时间间隔Δt内沥青分子的均方位移(MSD)[12]为

(2)

式中：M为沥青分子的均方位移，Γ为总模拟时间。

为考察沥青分子的均方位移随Δt的变化规律，在不同温度条件下，将基质沥青与改性沥青的分子结构模型稳定化后继续在NVT系综中运行500 ps，图5所示为相应沥青模型在363.15 K时的模拟结果。由图5可见，2种沥青及各自组分的均方位移与其流变特性相关，且随Δt增大逐渐呈现出线性变化规律。

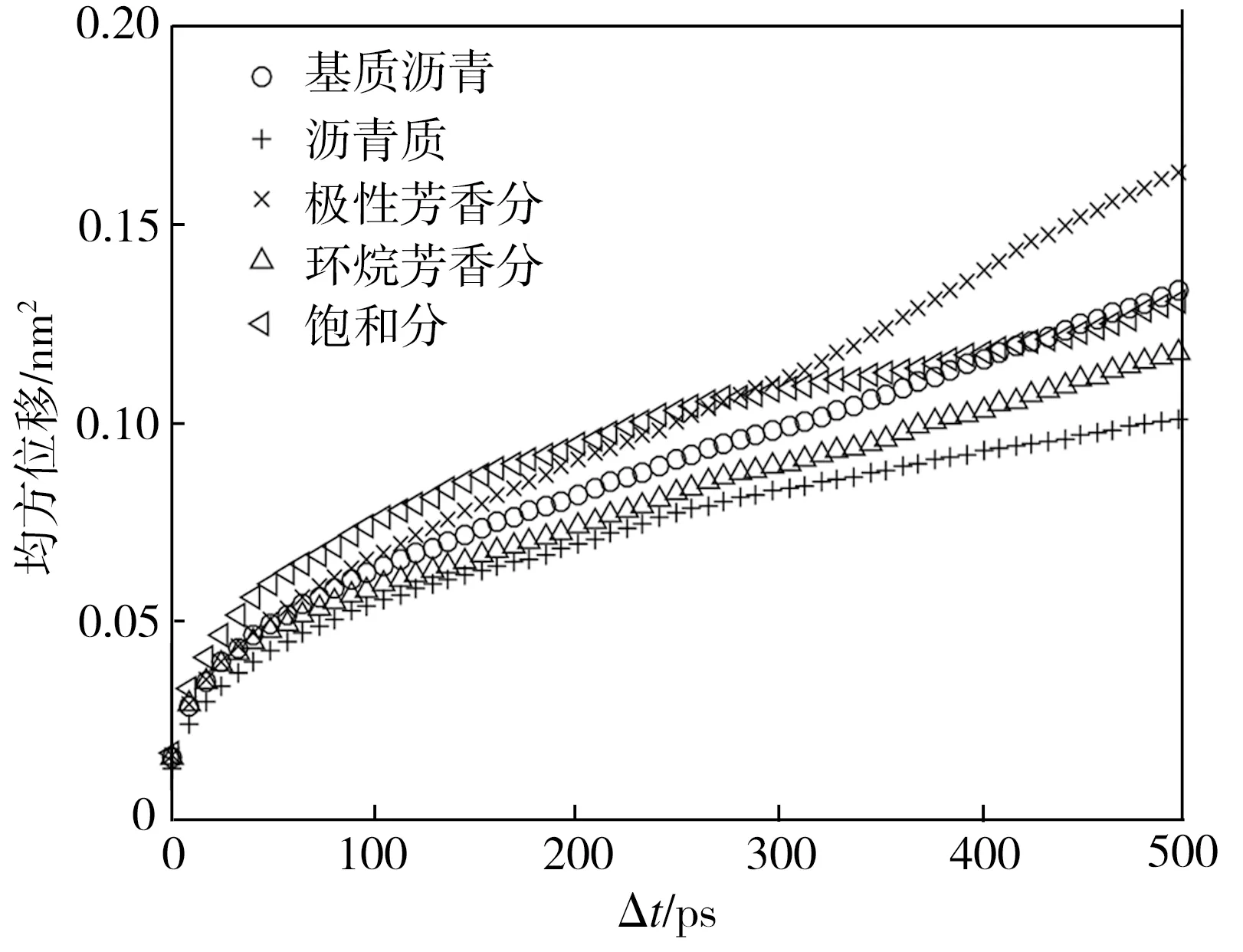
(a)基质沥青

(b)SBS改性沥青

基于不同温度条件下的模拟数据，可求得2种沥青及组分的扩散系数D[13]，计算公式为

(3)

计算结果见表2。由表2可见，沥青分子扩散系数均随温度升高而增大，且温度越高增大幅度越大；当温度不高于363.15 K时，改性沥青分子整体的扩散系数均大于基质沥青分子相应值，而在443.15 K时后者反超前者； SBS的添加能显著增大沥青质的扩散系数，但对沥青其它组分扩散行为的影响较复杂；在不同温度条件下，SBS改性沥青各组分扩散系数均以SBS为最小，沥青质相应值稍高于前者，其余组分如极性芳香分在298.15 K时扩散能力居中，但随着温度升高其扩散能力排序显著上升，而环烷芳香分的分子扩散能力始终处于中等水平，饱和分在298.15 K时较其它组分扩散系数最大，随着温度上升其扩散能力排序逐渐降低，当温度为443.15 K时仅高于沥青质与SBS。

因扩散系数D与体系温度T密切相关，本研究采用Arrhenius模型表示二者之间的关系，该模型最初是描述化学反应速率与温度关系的经验公式，现在广泛应用于各领域的分子扩散行为分析中，其表达式为

表2 沥青及其组分的扩散系数

(4)

式中，A为前因子，反映了高温条件或较长时间时沥青的自愈合能力；Ea为活化能，反映了发生自愈合所需要的初始能量[14]；R为普适气体常数(8.314 J/(mol·K))。利用2种沥青在不同温度下的扩散系数进行回归，得到其模型参数如表3所示。由表3可知，2个回归模型的判定系数r2均高于0.9，表明回归模型具有较高的精度。基质沥青的活化能Ea与前因子A均高于SBS改性沥青，这表明与基质沥青相比，改性沥青自愈合所需的初始能量较低，因中低温下条件下分子运动较慢，沥青自愈合性能主要取决于Ea，所以此时后者自愈合性能更佳；而高温条件下沥青的自愈合性能取决于前因子A，故基质沥青在高温条件下自愈合性能优于改性沥青。

表3 Arrhenius模型参数

4 结论

(1)沥青自愈合过程按沥青分子的运动特征可分为自由运动、互相渗透及无序化运动等3个阶段；

(2)根据计算模拟结果，沥青分子扩散系数均随温度升高而增大，且温度越高增大幅度越大；当温度不高于363.15 K时，SBS改性沥青分子整体的扩散系数均大于基质沥青分子相应值，而在443.15 K时后者反超前者。SBS的添加能显著增大沥青质的扩散系数，并且不同温度条件下，在SBS改性沥青各组分中， SBS的扩散系数最小。

(3)在中低温条件下，改性沥青的自愈合性能较基质沥青更佳，但高温时后者自愈合性能反超前者。