冲床下部凸轮顶料机构运动特性分析
2020-05-12郑建忠靳俊芳
郑建忠,靳俊芳
(宁波欧泰瑞克精密机械工业有限公司,浙江 宁波 315221)
凸轮顶料机构是压机常用的一种顶料形式,凸轮在顶料机构的作用是使顶杆在冲压过程中完成预期的运动规律,并将工件准确顶至预定位置。随着生产效率的提高,凸轮机构的运动速度越来越快,系统中运动元件的惯性力剧增,而且元件弹性变形的影响也会导致运动规律偏离预定的要求,产生不可忽视的动态运动偏差,尤其当凸轮的激振频率接近系统的固有频率时,执行元件的运动状态将远远偏离凸轮轮廓所限定的运动规律,并产生强烈的振动和噪声。
由于此问题的存在,必须将凸轮顶料机构当作弹性系统来分析。此类问题涉及弹性动力学,因此本文通过弹性动力学方法推导凸轮顶料机构系统自振频率和顶针的动态响应公式。
1 等效质量和等效刚度
1.1 等效质量
如图1所示为冲床下部顶料机构示意图,摆杆AOB绕O点转动,A为力输入端,B为力输出端,现在在输入端和输出端分别建立主动臂和从动臂的等效模型。
设主动臂AO绕O点的转动惯量为mA,其折算到A点的等效质量为,根据动能不变的原则可得公式:
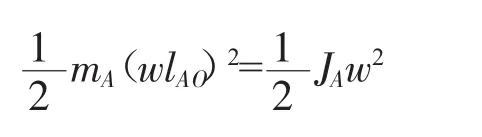
式中:w——角速度;
lA0——主动臂长。

图1 凸轮顶料机构示意图
同理可得等效质量:
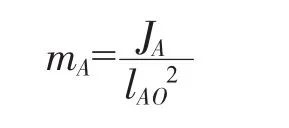
同理可得从动臂OB折算到B点的等效质量:

1.2 等效刚度
在凸轮顶料机构的动态分析中,各元件都视为弹性体,建立动力学模型时,需要将元件的刚度折算工作端,以一个具有等效刚性的弹簧来表达。
图2为主动臂AO的受力简图,由等截面悬臂梁挠度公式求得A点的变形量:
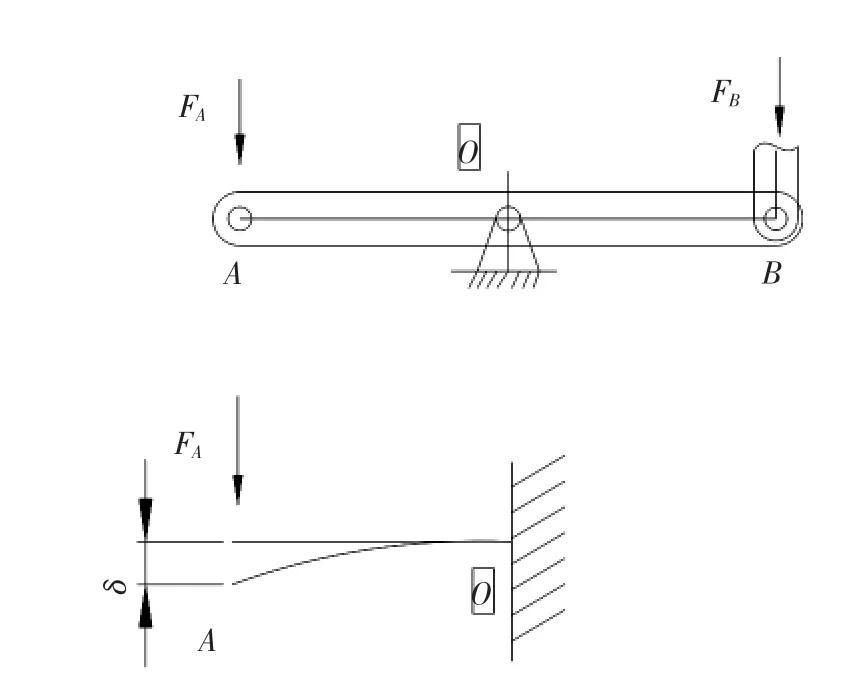
图2 主动臂AO的受力简图
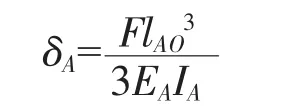
式中:EA——主动臂材料的弹性模量;
IA——惯性矩。
弯曲后的势能:

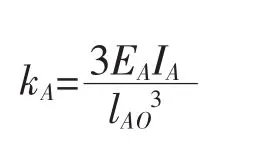
同理可得从动臂OB折算到B点的等效质量:

如果摆杆并非等截面,可以使用测试法测得刚度,刚度测试并非本文重点,这里不展开叙述。
接下来计算凸轮与轴的等效刚性,如图3所示,凸轮的弹性变形由两个原因引起,一是凸轮的角挠度,二是由于轴弹性变形引起的平行和垂直于从动件运动方向的偏移,平行从动件运动方向的偏移直接影响运动规律,其他影响较小,可以忽略。

图3 凸轮轴受力简图
凸轮轴在力F力的作用下平行于运行方向的凸轮中心截面处的挠度:

其变形势能


式中:Ec——凸轮轴材料的弹性模量;
Ic——凸轮轴的惯性矩。
由于只记平行于运行方向的变形,因而凸轮的等效质量等于凸轮本身的质量mc。
2 凸轮顶料机构的等效动力学模型
2.1 等效质量转移
将多自由度系统中离散的质量全部折算到顶针端,根据动能不变原则,摆杆A端上的等效质量(mA+mC),折算到 B 端:

因此顶针端等效质量

式中:mD——顶杆质量;
mE——弹簧质量,等效质量取弹簧质量的;
mF——顶针质量。
2.2 等效刚度转移
根据势能不变原则,摆杆A端上的刚度,折算到B端的等效刚度:

因此工作端等效刚性:

3 动态分析
为了更清楚说明激振对工作端运动的影响,忽略系统阻尼的影响,顶出阶段的振动方程可写为:

式中:y(t)——工作端的动态响应函数;
y0(t)——凸轮给定的激振函数。

函数y0(t)与凸轮轮廓有关,以本公司PT1-400机型为例,折算至顶针的运动规律为简谐运动规律,其运动方程为:

式中:h——顶针顶出高度;
th——顶出时间。
这两个参数是已知量,与凸轮轮廓和凸轮转速有关。因此,振动方程可改为
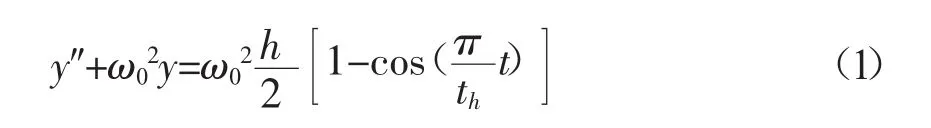
在振动问题研究中,常引入周期比,其值为激振周期与自振周期的比值其代入式(1)得:这是二阶微分方程,其初始条件为t=0时y=0,

解出方程可得顶出阶段的动态响应方程:
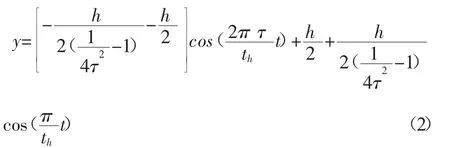
顶针速度为:
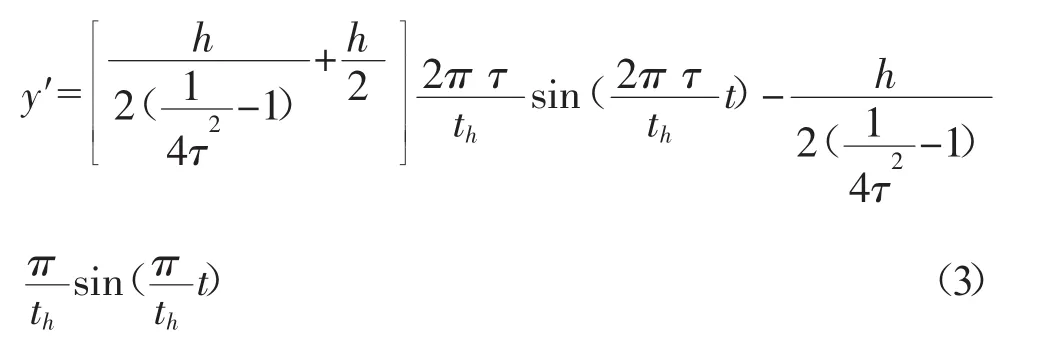
对于顶料机构料来说,顶出过程中的位移精度并不重要,重要的是顶出终端的定位精度。顶针顶至终端后将进行自由振动,这就是余振,余振的存在直接影响凸轮顶料机构的顶出定位精度,所以非常重要,余振时间区间为th~t,激振函数为 y0=h,因此
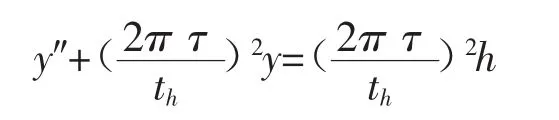
余振是在顶针顶至终端时开始,当t=th时y与y″和公式(2)(3)值分别相等,因此可以解出此二阶微分方程


这样,顶针顶出阶段和终端休止阶段的动态响应函数都已获得,作出动态响应曲线,如图4所示。从图中可以看出顶针的理论运动轨迹和动态响应轨迹存在差异。

图4 顶针运动轨迹图
由公式(4)不难算出,当 τ=1.5、2.5、3.5、4.5、......时,余振的位移误差 y-h=0,系统无余振,当 τ=1、2、3、4、......时,余振振幅达到最大值,随着 τ的增大,位移误差逐渐减小,绘出曲线如图(5)所示。
4 总结
顶针的动态响应误差随周期比τ的减小而增大,当τ减小到一定值后,余振振幅大幅增加,使行程终端无法正确定位,影响机械手夹取工件。顶料周期越快,系统中动力学的影响约明显。在设计高速凸轮顶料机构时,必须尽量减小元件的质量,提高系统的刚性,从而提高系统的自振频率。
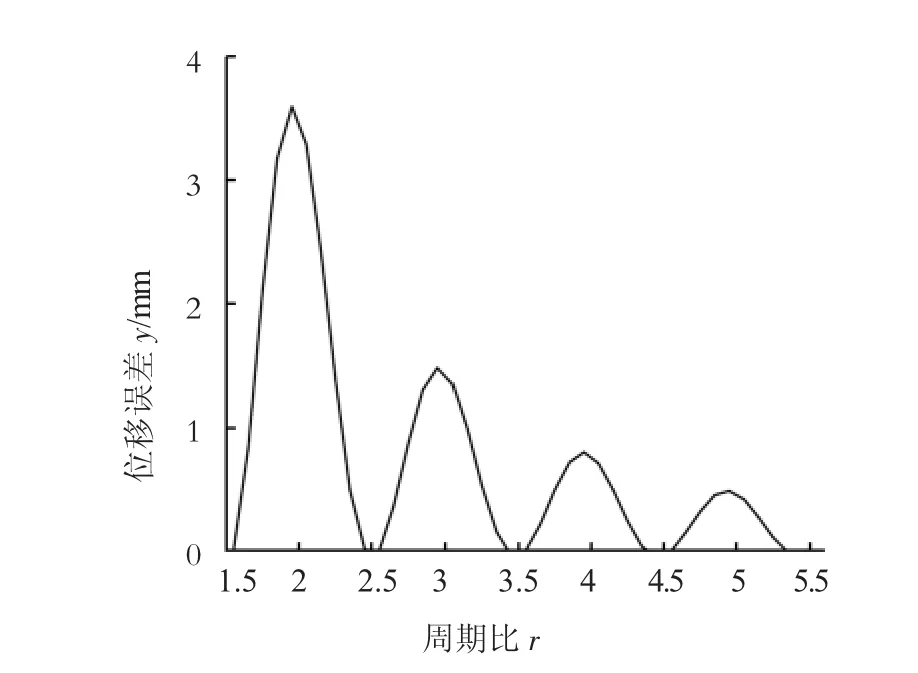
图5 位移误差-周期比曲线图
