基于预测和滑动窗口的轨迹差分隐私保护机制
2020-05-11叶阿勇孟玲玉赵子文刁一晴张娇美
叶阿勇,孟玲玉,赵子文,刁一晴,张娇美
(1.福建师范大学数学与信息学院,福建 福州 350007;2.福建省网络安全与密码技术重点实验室,福建 福州 350007)
1 引言
近几年来,随着具有定位功能的智能终端和移动通信技术的迅猛发展,各种基于位置的服务(LBS,location based service)日益普及,现已覆盖国民经济和社会生活的方方面面,如导航、兴趣点查询与推荐、外卖、签到、社交网络等[1]。然而,LBS 为人们的日常生活带来极大便利的同时,也产生了位置隐私泄露问题。其中尤其突出的是,位置服务提供商可能会利用数据挖掘等技术,从用户提交的位置信息中非法获取用户的敏感信息,如家庭/工作地址、消费水平、健康状况、生活习惯等[2]。
地理不可区分性[3]隐私保护模型是目前LBS 位置隐私保护中常见的方法,它将差分隐私[4]引入几何空间中,克服了传统k-匿名等模型普遍存在“依赖于攻击者背景知识而导致其安全性无法严格证明”的缺点。地理不可区分性模型是通过极坐标系下的Laplace 扰动机制向用户位置添加受控噪声,使攻击者几乎无法区分近似位置与真实位置的差异,从而将用户真实位置保护在一个半径为r的圆形区域内。位置差分隐私的定义是建立在严格数学统计模型上,并可通过调整隐私参数来控制隐私保护水平,因此备受关注。然而,现有的位置差分隐私保护研究仍然存在以下两方面的问题。
1)现有的位置差分保护机制仅适用于单次或零星查询,多次查询仍有可能暴露用户的真实位置。因为连续查询的位置间存在时空相关性,服务查询不仅会消耗当前位置的隐私成本,而且也会增加其他位置的隐私消耗,即差分隐私具有序列组合特性。因此,单个位置满足ε-差分隐私,并不能确保轨迹满足ε-差分隐私。
2)现有的差分隐私保护技术并没有很好地解决隐私风险与服务质量间的矛盾问题;位置差分隐私中,每个扰动的位置输出具有一定的随机性,隐私预算越小,隐私保护程度越高,但是该位置的服务质量会越差。隐私风险与服务质量顾此失彼,难以得到平衡。
位置预测是指通过观察已公开的信息(如历史发布的轨迹)来预测用户当前的位置。由于预测机制与用户当前的真实位置无关,不会给攻击者提供更多有用信息,因此隐私损失非常小,甚至可视为0。因此本文尝试利用预测机制替代差分扰动,以节省隐私开销,即降低隐私风险。基于上述分析,本文提出一种基于预测和滑动窗口的轨迹差分隐私保护机制,主要贡献如下。
1)提出一种融合预测扰动的差分查询机制,以降低连续查询的隐私开销。首先,利用马尔可夫链和指数扰动机制预测满足差分安全和时空相关性约束的查询位置。然后,引入服务相似地图机制检测预测位置的可用性,如果满足可用性要求,则采用预测位置查询,否则使用差分扰动的位置查询。
2)设计基于w滑动窗口的轨迹隐私预算分配机制,确保轨迹中任意连续的w次查询隐私消耗累计不超过ε,即确保轨迹满足ε-差分隐私,从而解决连续查询的位置隐私安全问题。
3)设计基于敏感度地图的位置隐私差异化保护机制。通过允许用户自定义位置的敏感度,实现隐私预算的量身定制,进一步提高隐私预算的利用率。
4)利用真实数据集对本文方案进行实验分析,验证方案的有效性。
2 相关工作
在过去的几年中,研究者已提出许多的位置隐私保护方案和技术。根据保护机理的不同,本文将其分为匿名和扰动两大类。
k-匿名[5]是目前最被广泛应用的位置隐私保护机制。其思想是采用一个包含至少k-1 个用户的区域来替代用户的实际位置,用于向LBS 请求服务。在该定义中,用户的身份至少与k-1 个人不可区分,从而有效地解决不可信服务器带来的身份隐私泄露问题。例如,Niu 等[6]提出了一种虚拟位置选择算法来实现LBS 中用户的k-匿名性。Hwang 等[7]提出了一种基于历史轨迹的时间模糊算法。在该算法中,TTP 在选定k-1 条历史轨迹后,扰动每个查询轨迹的时间序列,产生空间和时间的双重混淆。Wang等[8]对位置k-匿名的有效解决方案进行了研究,并定义了一种用于初始化位置k-匿名的概率模型PkA(probabilistick-anonymity framework),也证明了DLS(dummy-location selection)算法属于PkA。
位置扰动是指用户请求LBS 时,以假位置替代或者混合自身的真实位置,从而保护位置隐私。例如,文献[9]提出一种基于假查询的连续位置服务隐私保护机制,该机制根据邻居节点的运动速率和方向预测将来的轨迹;在此基础上,选出轨迹与查询用户相近的k-1 个邻居节点;在匿名处理时,通过发动这些邻居节点插入假查询,来构造虚假的连续查询。Andres 等[3]基于差分隐私的思想提出了地理不可区分性的位置隐私模型,并设计了一种极坐标下的Laplace 机制产生假位置,以实现位置隐私保护。文献[10]在文献[3]的基础上将差分隐私机制看成是最优化问题,提出了一种基于δ-spanner 的近似解决方案。Xiao 等[11]用马尔可夫链表示位置上的时序关系,并重新定义相邻数据集的概念,提出了一种基于凸包的差分隐私位置发布机制。Hua 等[12]提出了在短时间连续查询时,基于差分隐私的位置隐私保护方法,解决了连续查询时隐私风险与查询次数成线性增长的问题。吴云乘等[13]基于马尔可夫概率转移矩阵,分析了发布位置对当前真实位置和之前真实位置的影响,提出了一种差分隐私位置发布机制(DPLRM,privacy location release mechanism),以保护用户的位置和轨迹隐私。Chatzikokolakis 等[14]提出一种预测扰动机制(PM,predictive mechanism for mobility trace),利用预测位置替代真实位置,解决连续查询的隐私与可用性的两难问题。
3 背景知识
3.1 位置差分隐私
定义1ε-差分隐私。∀x,x'∈X,在查询机制M下输出的位置o,若满足式(1),则称算法M满足ε-差分隐私

其中,M(x)(o)为原始输入x在扰动机制M下输出结果为o的概率,该定义表明2 个原始输入越接近,则输出同一位置的概率越高,即2 个源位置不可区分,从而达到保护用户位置隐私的目的;ε为一个距离单位的隐私预算,代表隐私保护的程度,ε越小,隐私保护程度越高,当ε=0 时,隐私保护程度最高,表示没有泄露用户的任何隐私。
dx(x,x')是测量矩阵,不同的dx(x,x')模型可以解决不同应用场景的差分隐私问题。如数据库查询隐私保护模型中[4],dx(x,x')=1 表示2 个统计数据库x和x'仅相差一条纪录。该模型保证数据集中增加和删除任意一条记录都不会影响输出的结果,即无法得知数据集中是否存在某条记录,从而达到保护数据隐私的目的。该定义只是理论上的一个模型,而要实现具体的保护则需要噪声机制的介入。对于数值型数据和非数值型数据,主要的噪声机制分别为Laplace扰动机制和指数扰动机制,具体说明如下。
定义2Laplace 扰动。对于数据集D上的任意一个函数f:D→Rd,若函数f的输出结果满足式(2),则f满足ε-差分隐私。

其中,Δf为查询函数的敏感度。Laplace 分布的位置参数为0,尺度参数为。
定义3指数扰动。给定一个可用函数f:(Dn×R)→Ω,r是可用函数输出域range 中的一个实体对象,若函数f的输出结果满足式(3),则f满足ε-差分隐私。其中,S(f)为可用函数的全局敏感度,对象被选中的概率正比于可用函数f的打分。指数机制以正比于的概率返回实体对象。

若dx(x,x')=d2(x,x'),则代表2 个地理位置间的欧氏距离,此时该模型可用于保护LBS 位置查询时的隐私泄露问题,本文称其为ε-地理不可区分性,该定义等价于欧氏距离空间中的ε-差分隐私。
定义4ε-地理不可区分性[3]。对于任意满足d2(x,x')≤r的2 个位置x和x',若在查询机制M下输出的位置集o满足式(4),则称M满足ε-地理不可区分性。
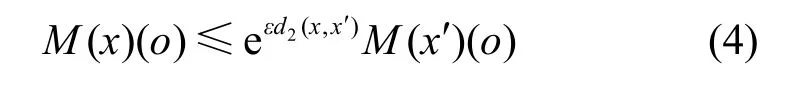
其中,M(x)(o)是在查询机制M中,位置x输出位置o的概率。ε为一个距离单位的隐私预算,则任意半径r的隐私预算为ε=εr,此时用户的真实位置被保护在半径为r的圆中。可以看出,2 个位置的地理距离越近,生成相同查询位置o的概率越相似,地理位置越不可区分,隐私保护程度越高。进一步,利用其极坐标下的Laplace 机制产生满足ε-地理不可区分性的噪声位置(假的查询位置),实现该模型的隐私保护。
此外,ε-差分隐私具有序列组合特性,即如果每个发布机制Mi满足εi-差分隐私,则Mi的一个序列应用则满足∑εi-差分隐私。此性质指出,当查询机制应用n次LBS 查询服务时,每个噪声位置的隐私预算为ε,则轨迹的隐私预算为nε。
定义5w连续序列ε-差分隐私。假设用户的轨迹为Z={z1,z2,z3,...,zn},其中zi为在查询机制Mi下输出的假查询位置,并且Mi满足εi-差分隐私。对于其中任意一个w个时间戳的连续位置序列子集{zi-w+1,…,zi},若其隐私预算之和满足式(5),则用户的轨迹隐私满足w连续序列ε-差分隐私。

定义6δ-位置集[11]。假设用户在t时刻有n个可能的位置,令表示用户在各个位置的概率值,则δ-位置集为累积概率值不少于1-δ的最小位置集,即

直观而言,δ-位置集是用于删除可能位置集中概率比较低的位置点。
3.2 相似地图
LBS 中,用户通过向服务提供商提供自身位置获取相关服务。但是由于地理位置的空间特征,不同位置的查询结果可能是相同或相似的。因此定义服务相似度,具体如下。
定义7位置的服务相似度[15]。假设有2 个位置g和h,则它们的服务相似度定义为

其中,(xi,yi)是位置i的坐标,Rm(x,y)是在坐标(x,y)处查询的top-m个兴趣点的排序结果集,是集合元素的数量。
通过服务相似度对地图进行服务相似性分区[15],将查询结果相同的位置集(服务相似度为1)合并成一个区域,即同一个分区内的任一位置的查询结果是相同的。因此相似地图定义如下。
定义8相似地图。给定一个服务区域S,若S=Si∪S,Si∩Sj=∅,以及对其中任意的p1,p2∈Si,sim(p1,p2)=1,则称S为相似地图。显而易见,在同一相似区域Si的任意位置的查询结果是相同的。
选取某一地区的870 km2区域内分布的麦当劳餐厅位置,并将该区域划分为一个300×290 的网格,每网格的面积为100 m×100 m,并取top-3结果集,生成相似区域(用同一灰度值进行标识),如图1 所示。

定义9位置正确率。查询机制M的位置正确率为其中,R(p)表示在真实位置p处查询的兴趣点的结果集,M(p)表示真实位置p在查询机制M下输出的假位置查询点,S[.]表示集合数量。

图1 相似区域
4 系统方案
根据观察发现,预测位置往往随机分布在真实位置的周边,攻击者无法根据预测位置推测出用户的真实位置,因此可以将预测机制视为一种随机扰动。由于预测机制的隐私开销非常小,甚至趋近于0,因此利用预测机制替代差分扰动能够有效降低连续查询的隐私开销。其次,隐私具有差异化,为不同的语义位置分配不同的隐私预算,能够有效提高隐私预算利用率。例如,可以为医院/家庭等敏感位置分配较小的预算,而公园/商场等公共区域分配较大预算,从而实现隐私预算的合理分配,节省隐私开销。再者,由于查询位置具有时空关联性,单个位置满足ε-差分隐私,并不能确保轨迹隐私安全。因此基于上述观察,本文提出一种基于预测和滑动窗口的轨迹差分隐私保护机制,主要包含以下策略。
1)隐私预算量身定制
该机制允许用户自定义位置敏感度,并依此量身定制隐私预算,进一步提高轨迹隐私预算的利用率。
2)预测扰动
利用马尔可夫链和指数扰动机制获得满足高可用性、差分安全和时空相关性约束的预测位置,并引入服务相似地图校验预测位置的可用性。该策略利用预测的假位置替代差分扰动,从而有效降低预算开销,并进一步提高服务质量。
3)基于w滑动窗口的隐私预算分配机制
采用w滑动窗口机制分配连续查询中各位置点的隐私预算,确保轨迹中的任意w个时间戳(位置点)的隐私消耗累计不超过ε,即确保轨迹满足ε-差分隐私。
具体查询过程如算法1 所示。
算法1基于预测和滑动窗口的轨迹差分隐私保护机制
输入Q(t-1),L(t-1),p,mapsen,U,θ,w,α,δ,mapsim,ε,C,E,N
输出z

算法1 中,θ为用户设置的敏感度阈值;p为用户的真实位置;p.pl 为真实位置的敏感度;lookup为查询函数,即通过查找敏感度地图mapsen,获取p.pl;L(t-1)为用户在前一时刻的可能位置集;Q(t-1)为用户在前一时刻的可能位置概率;w为滑动窗口;δ为δ-位置集的参数;α为用户设置的服务相似度阈值;mapsim为相似地图;ε为用户设置的轨迹隐私预算之和;C、E和N分别为隐私预算分配机制中用户设置的参数;U为状态转移概率矩阵;prediction(U,εe,δ,Q(t-1),L(t-1))为基于马尔可夫链和指数扰动机制的预测机制,详见算法2;test(l,α,mapsim,p,εθ)为基于服务相似度的检测函数,详见算法3;N(εN,p)为当隐私预算为εN时,位置p在地理不可区分性的扰动机制中输出噪声位置,即z。在算法1 中,首先根据用户的真实位置获取位置的敏感度。如果位置的敏感度小于用户设置的阈值θ,则检测成功,直接利用用户的真实位置获取服务(算法1 的①~③);否则通过隐私预算分配机制,分别获取预测机制和检测函数的隐私预算εe和εθ(算法1 的⑤~⑥)。算法1 的⑦~⑨是利用该预测机制获取预测位置点l,并检测预测位置的可用性。如果检测成功,直接采用预测的位置作为查询点;否则,通过隐私预算分配机制,获取地理不可区分性的隐私预算εN,并进行随机扰动,即N(εN,p),将噪声位置作为当前的查询位置(算法1 的⑩~⑫)。
4.1 敏感度处理
文献[13]认为只有与敏感位置直接相连的语义位置才具有敏感度。然而,从随机扰动的分布角度看,那些靠近敏感位置的语义位置,即使与敏感位置不直接相连,仍然存在暴露敏感位置的风险,因此也应分配一定的敏感度。因此,本文考虑了位置点间的整体连通性,根据距离和出入度将敏感位置的隐私级别分别辐射给附近节点。首先,获取敏感位置附近具有隐私级别的位置节点集,即连接集neighborSet。然后,将地图转化为无向图,根据距离和出入度,则任意位置g与敏感位置a的等价距离为g.eDis=ED(c-1),其中,ED为g与a的欧氏距离,c为两位置节点间最短路径所经过的节点数-1。进一步地,neighborSet={g|g.eDis<b},其中b为用户设置的阈值。最后,为敏感位置a的连接集neighborSet 中的任意位置g分配隐私敏感度,如式(9)所示。

其中,g.pl 表示节点g分配的隐私敏感度。
为了计算方便,本文将地图网格化。然后,利用上述过程计算地图中各区域的敏感度,生成敏感度地图mapsen。mapsen存储于手机端,用户可以在离线阶段获取位置的敏感度。
4.2 预测机制
预测机制主要由基于马尔可夫链和指数扰动机制的预测机制和基于服务相似性的检测机制两部分构成。
针对预测机制的部分,本文利用马尔可夫链刻画用户真实位置间的时序相关性,其中,状态转移概率矩阵U表示真实位置在区域间的转移可能性,如状态转移概率矩阵U中元素uij表示用户从第i个区域移动到第j个区域的概率。这里假设状态转移概率矩阵U可事先在历史记录上计算得到。假设用户在t-1 时刻产生的可能位置集为,其概率值为,通过状态转移概率矩阵计算出t时刻的可能位置为,其概率值为,其中Q(t)=Q(t-1)U。由于通过转移矩阵计算t时刻位置集中的一些元素的概率较低,因此本文用δ-位置集(见定义6)过滤概率较低的元素,得到候选集ΔXt。然而对于选择ΔXt中的元素作为预测位置点,需要选择概率较高的元素。为了隐私性,本文选取指数机制对其选择,即E(εe):ΔXt→l,其中,εe为指数选择机制的隐私预算;打分函数为,m为δ-位置集中的元素个数。具体算法如算法2 所示。该机制对输出结果添加了噪音,但是概率高的元素仍以较大的概率输出,从而使输出结果更加隐私并更合理。
算法2预测机制
输入L(t-1),Q(t-1),U,δ,mapsim,p,ε,E,w
输出l

通过隐私预算分配机制,本文分别获取指数机制的隐私预算εe(算法2 的③)。E(εe,ΔXt)为隐私预算为εe时,通过指数扰动机制在ΔXt中输出预测位置l。在算法2 中,本文首先利用马尔可夫链计算当前时刻的可能位置集,再利用δ-位置集ΔXt过滤其中概率较低的位置点,最后采用指数机制选出当前预测位置。
针对检测的部分,为了评估预测位置的服务质量,本文提出一种基于服务相似性的检测函数。其中基于服务相似性的检测函数θ(εθ,α,l)为
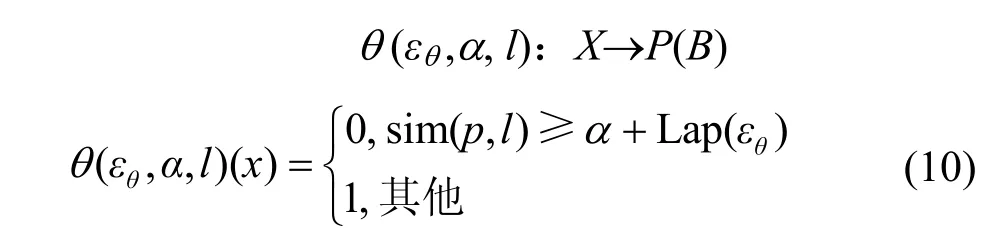
其中,l是预测位置;sim(p,l)是位置p与l的服务相似度;B={0,1}是布尔函数,输出“0”表示预测成功,“1”表示预测失败;Lap(εθ)表示隐私预算为εθ时Laplace 扰动值。由于检测函数必然会泄露用户部分的位置隐私,为了保证安全,本文在检测函数中也引入Laplace 的扰动机制。虽然检测函数用掉一部分隐私预算,但是其相对满足ε-地理不可区分性的扰动隐私预算值较小,因此节省了隐私预算,同时提高了服务质量。服务器预先生成相似地图mapsim,供客户端下载,从而在离线阶段通过相似地图检测2 个位置的服务相似度。对于该检测机制,其具体过程如算法3 所示。
算法3检测机制
输入α,l,mapsim,p,C,ε,w
输出O

算法3 中,l为预测的位置。算法3 利用算法2预测输出的预测位置l,与真实位置进行服务相似度的检测。如果满足可用性需求记为0,否则记为1,并相应输出。
4.3w序列满足ε-差分隐私的隐私预算分配机制
从查询机制可知,每个位置在指数扰动阶段、检测函数检测阶段和地理不可区分性的扰动阶段分别需要分配的隐私预算为εe、εθ和εN。如果一个时间戳的假位置预测成功,利用预测位置作为查询位置。生成查询位置的过程共经历了指数扰动机制和检测函数2 个阶段,因此花费的隐私预算为εe+εθ。如果检测失败,则利用地理不可区分性的扰动产生查询点,其经历了3 个阶段,因此花费的隐私预算为εe、εθ和εN之和,则有
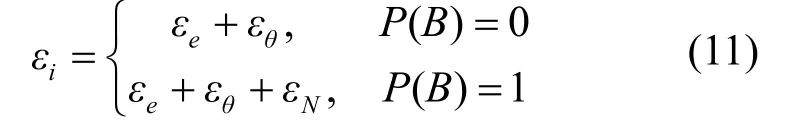
其中,εi为连续的LBS 查询中,第i个查询位置分配的总隐私预算。若P(B)=0,预测成功,反之预测失败。从式(11)也可以看出,如果预测失败,反而花费更多的隐私预算,因此要提高预测成功率,节省隐私预算。
从差分隐私的序列组合特性可以看出,在连续的LBS 查询中,无法保证轨迹的隐私。因此本文考虑将轨迹片段化,引入w滑动窗口机制,使其轨迹满足w连续序列ε-差分隐私。首先,w滑动窗口是指用户连续查询的时间戳长度为w的位置序列,其形式如图2 所示。轨迹中任意一个时间戳为一个窗口,每个窗口对应的隐私预算为εi。其次,设计隐私预算分配机制为εe、εθ和εN分配相应的隐私预算。
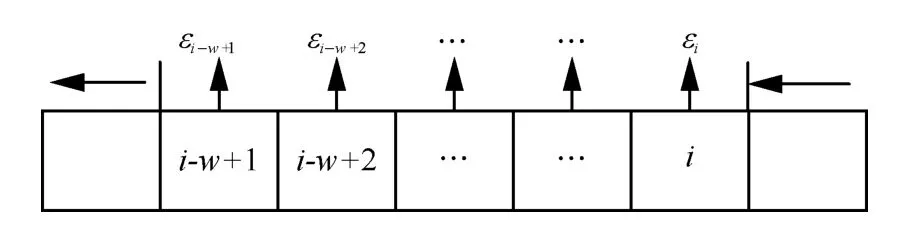
图2 w滑动窗口示意
为了使轨迹满足ε-差分隐私,引入参数E、C和N调节隐私预算,且E+N+C=1,具体预算分配机制如下。
对于指数扰动机制,每个位置分配到的隐私预算εe为

指数机制中的打分函数为f=Q(t)={q1(t),...,qm(t)},由于序列组合特性,因此δ-位置集中的每个位置分配的隐私预算为。
对于检测函数检测阶段,每个位置分配到的隐私预算εθ为

由于隐私具有主观性,在每一点上进行同等扰动并不合理。不仅用户对不同语义位置的敏感度不同,而且不同用户对同一个语义的敏感性也是存在差异。因此,本文引入敏感度量身定制策略,提高隐私预算的利用率。对于敏感度越高的位置,分配较小的隐私预算,即加入越大的扰动噪音,从而获得更高的隐私保护程度。首先,对于初始值(r,θ)分配相应的隐私预算。其中(r,θ)指半径为r,敏感度为θ。其次,考虑位置敏感度,敏感度越高,对于噪音扰动阶段分配的隐私预算越低,保护半径越小。因此,对于任意敏感度g.pl,其半径的选择为,从而对于满足地理不可区分性的扰动,每个位置分配到的隐私预算εN为
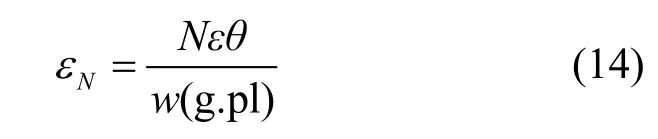
其中,E+C≤N且g.pl∈[θ,1]。为了节省隐私预算,在预测阶段的预算值要小于扰动阶段的预算值,因此E+C≤N。
5 隐私分析
本节证明本文查询机制的发布轨迹能够满足w连续序列ε-差分隐私。
根据定义5,本文首先可以证明E(εe)、θ(εθ,α,l)和N(εN)分别满足εe-差分隐私、εθ-差分隐私和εN-差分隐私。从而,可以进一步证明本文查询机制Mi满足εi-差分隐私,其中εi=εβ+εθ+εN。证明过程见附录。
基于上述分析,本文可以证明轨迹满足w连续序列ε-差分隐私,即本文机制的轨迹中任意连续w个位置的隐私预算之和为ε。形式化表达如定理1所示。
定理1任意一个w个时间戳的连续发布位置序列子集{zi-w+1,…,zi},轨迹隐私保护满足w连续序列ε-差分隐私。即

证明首先E(εe)、θ(εθ,α,l)和N(εN)分别满足εe-差分隐私,εθ-差分隐私和εN-差分隐私,由于本文机制由这3 种机制组合而成,因此查询机制Mi满足εi-差分隐私,其中εi=εβ+εθ+εN。因此对于任意w个时间戳的隐私预算之和为

证毕。
6 实验分析与评估
本文分析了模型参数在2 种真实数据集中对于可用性的影响。同时,将本文方案与DPLRM[13]机制和PM[14]机制进行对比分析,从而验证本文方案的有效性。
6.1 实验数据集与设置
实验采用Geolife[16]和Gowalla[17]这2 个数据集,其中,Geolife 采集了182 个用户2007 年4 月至2012 年8 月在北京活动的真实数据,共包含17 621 条轨迹。数据集包含用户编号、时间戳、经度、纬度、海拔等信息。本文从该数据集中抽取50 条北京某一地区的轨迹进行采样,采样方法如下。每隔1 min 采取一个样本点作为用户的查询点,如果2 个连续位置的间隔大于1 min,则该位置被随机取样。50 条轨迹采样后大约有500 个位置。为方便计算,本文将地图划分为300 m×300 m 的网格,并将用户真实位置规格化到网格中心。Gowalla 采集了15 116 个用户2009 年2 月至2010 年10 月在移动社交网站上(美国加州范围内)的签到数据。同Geolife 一样,本文抽取加州范围内的用户编号、时间戳、经度、纬度作为新的数据集,并将其地图划分为0.89 m ×0.89 m 的网格。
6.2 可用性评估
本文发现预测成功率会直接影响LBS 的可用性与隐私风险,因此提高预测成功率对基于预测机制的隐私保护方案至关重要。可用性阈值α与预测成功率的函数关系如图3 所示,并引入PM 方案进行对比。从图3 可看出,两者的成功率都随着α的升高而逐渐下降,但本文的预测成功率始终明显高于PM 方案。这是由于在基于服务相似性的检测函数中,α越大,满足可用性要求的位置越少,因此预测成功率必然下降。此外,本文方案采用了马尔可夫链的预测机制,能够有效提高预测成功率。
本文利用定义9 的轨迹中位置正确率的平均值和真实位置与其发布位置之间的均方根误差(RMSE,root mean square error)这2 种测量矩阵去测量的轨迹的可用性。其中,用户真实轨迹位置和查询位置轨迹分别为P={p1,p2,…,pn}和Z={z1,z2,…,zn},则
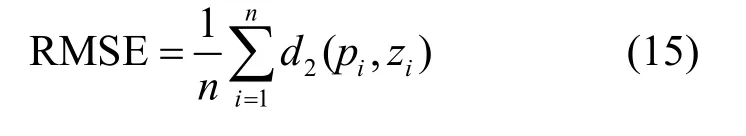
首先,本文分别分析敏感度阈值θ在Geolife和Gowalla 数据集中对RMSE 和位置正确率的影响,结果如图4 和图5 所示。在该实验中,w=3,α=0.5,ε=1.8,b=500,。从图4中可以看出,本文方案的可用性随着θ的升高而提高。θ越高,一方面,在扰动阶段每个位置分配到的隐私预算提高,可用性也提高;另一方面,更多位置的敏感度小于θ,从而不需要扰动,因此可用性更好。但是当θ取值为0.16 时,RMSE 为0。这是因为在本文的敏感度划分方法中,当b设置为500时,地图内区域的敏感最高为0.15。因此当θ取值为0.16 时,地图中所有位置都是不敏感位置,直接发布,因此轨迹的平均RMSE 为0。此外,Geolife数据集中的可用性好于Gowalla 数据集,因为Gowalla 数据集划分区域的网格较大,2 个位置间的距离较远,所以可用性较差。最后,本文的可用性高于PM 方案和DPLRM 方案。首先,本文的预测成功率高于PM 方案。其次,因为PM 方案不考虑隐私的个性化设置,隐私预算的利用率低,扰动不确定性高,可用性差。DPLRM 方案虽然考虑隐私与可用性的平衡,但是在隐私中既考虑发布位置对当前位置影响,又考虑了对之前位置影响,限制因素较多,并且本文方案中引入了可用性检测,故可用性高。

图3 可用性阈值α与预测成功率的函数关系
从图5 中可以看出,位置正确率随着θ的增大而提高。因为从图4 中得到,θ越大,RMSE 越小,因此位置正确率越高。当RMSE=0 时,正确率最高,接近于1。此外,Geolife 数据集中的可用性也高于Gowalla 数据集,同时本文的位置正确率也高于DPLRM 方案和PM 方案。

图4 敏感性阈值θ对RMSE 的影响

图5 敏感性阈值θ对位置正确率的影响
本文还应该探究在给定轨迹隐私预算,滑动窗口长度与可用性的关系和给定滑动窗口轨迹的隐私预算与可用性的关系。但是二者之间的本质问题是相同的,都是探求隐私预算与可用性的关系,因此,本文分析滑动窗口长度对可用性的影响,结果如图6 和图7 所示。在这一系列实验中,本文假设ε=1.8,b=500,θ=0.01,α=0.5。从图6 中可以看出,RMSE 随着滑动窗口w的数量增大而提高。w越大,每个位置分配的隐私预算越少,则预测成功率越低,并且满足地理不可区分性的扰动越大,从而降低了隐私可用性。Geolife 数据集中的可用性好于Gowalla 数据集,与图4 的原因相同。本文的可用性高于DPLRM 方案和PM 方案。DPLRM 方案对于发布位置的约束条件较多,从而导致较远的位置满足约束条件,并且本文方案中引入了可用性检测,可用性高。PM 方案利用前一次的查询点作为检测位置点,然而本文中进一步改进利用基于服务相似性检测以及马尔可夫模型的预测机制,预测成功率更高,因此可用性最好。
图6 w滑动窗口对RMSE 的影响
从图7 中可以看出,位置正确率随着滑动窗口w数量的上升而降低,同时Geolife 数据集中的可用性也高于Gowalla 数据集,此外,本文方案的位置正确率也高于DPLRM 方案和PM 方案。
6.3 系统运行时间评估
图7 w滑动窗口对位置正确率的影响

图8 θ对方案运行时间t的影响
本节评估了本文算法的时间开销,并与DPLRM 方案比较,如图8 所示。为了更加方便比较,本文的实验设置与DPLRM 算法相同,选取数据集为Geolife 数据集,将北京地图划分为大小为0.34 km×0.34 km 的网格,初始敏感位置个数设为10,并且敏感度计算方法也与DPLRM 相同。从图8可以看出,本文方案的运行时间远远小于DPLRM方案。DPLRM 方案中最耗时的部分在于计算其后验概率,其复杂度为O(wN3),其中N为用户t时刻可能的真实位置区域个数和满足限制条件的发布区域个数。可能的真实位置区域个数也是由马尔可夫链计算的,如果查询时间较长,则可能的真实位置区域个数非常大,在实际应用中需要多个服务器并行计算。而在本文方案中,指数选择与地理不可区分性的计算时间与可能区域的个数呈线性增长。此外,利用转移矩阵计算可能位置的概率,这部分计算DPLRM算法也已经包括,并且开销也很低。
7 结束语
为解决轨迹差分隐私保护中存在的隐私预算与服务质量等问题,本文提出一种基于预测和滑动窗口的轨迹差分隐私保护机制。首先,允许用户自定义位置敏感度,并依据敏感度量身定制隐私预算,提高预算的利用率。其次,利用马尔可夫链和指数扰动机制获得满足高可用性、差分安全和时空相关性约束等3 个目标的预测位置,并引入服务相似地图校验预测位置的可用性。该策略可以有效降低预算开销,并进一步提高服务质量。最后,采用滑动窗口w机制分配连续查询中各位置点的隐私预算,确保轨迹中的任意w个时间戳(位置点)的隐私消耗累计不超过ε,从而实现连续查询的轨迹满足ε-差分隐私。今后将考虑研究如何对本文算法进行继续优化,以提高查询的可用性。
附录 查询机制Mi 满足ε i-差分隐私证明
对于指数扰动机制、检测函数检测与噪音扰动机制分别满足ε-差分隐私,即
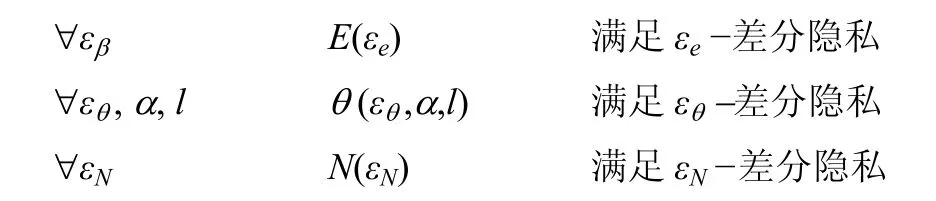
则查询机制Mi满足εi-差分隐私,其中εi=εβ+εθ+εN。
证明
在预测阶段选取的机制为指数机制,因此E(εe)满足εe-差分隐私,其中dx(p,p')=1。
在检测函数检测阶段,有
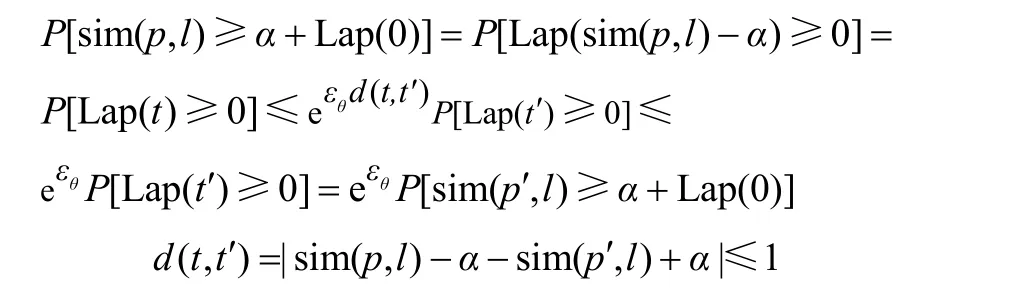
因此,∀εθ,α,l,检测函数检测θ(εθ,α,l)满足εθ-差分隐私,其中dx(p,p')=1。
在位置扰动阶段选取的机制为基于地理不可区分性的扰动,因此N(εN)满足εN-差分隐私。
根据序列组合特性,εi=εe+εθ+εN。因此,查询机制Mi满足εi-差分隐私。
证毕。
