移动性感知的边缘服务迁移策略

吴大鹏，吕吉，李职杜，王汝言

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.重庆高校市级光通信与网络重点实验室，重庆 400065；3.泛在感知与互联重庆市重点实验室，重庆 400065）

1 引言

随着移动互联网的不断发展，虚拟现实、智能家居等资源密集型应用在人们的生产和生活中发挥着越来越重要的作用[1-2]。这些应用通常具有超低时延和海量数据处理等需求，给储能、计算及缓存能力有限的移动设备带来了极大的挑战。移动边缘计算网络把移动边缘计算（MEC,mobile edge computing）与移动云计算（MCC,mobile cloud computing）的各自优势相结合，为这些应用需求提供了新的解决思路[3-4]。然而，如何为移动中的设备（如车辆、轨道交通等）提供连续不间断的服务是制约移动边缘计算网络进一步提高用户服务质量的瓶颈之一。

在移动边缘计算网络中，由于用户的移动性、服务请求的多样性及区域请求量的差异性，容易造成边缘服务器负载不平衡、热点地区网络拥塞等问题，从而严重降低用户的服务质量。虽然边缘服务迁移技术能够保证为用户提供连续化服务，而且还能平衡边缘服务器之间的工作负担，但受限于移动边缘计算网络的通信能力、计算资源及存储容量，如何根据用户的实时位置信息快速、高效地进行边缘服务迁移，成为移动边缘计算网络动态服务迁移中待解决的关键问题之一。

本文从实际情况出发，提出了一种移动性感知的边缘服务迁移策略，考虑到用户的运动轨迹具有部分可预测性及服务请求类别的多样性，对用户的服务迁移决策与移动边缘计算网络的通信-计算-存储资源进行了联合优化。本文主要贡献如下。

1)通过Lyapunov 优化理论有效地将长期迁移成本预算转换为实时优化，在不需要任何用户位置先验信息的条件下，根据用户的实时位置信息进行快速、高效的在线服务迁移，克服了由于用户运动轨迹的随机性而导致的无法建立马尔可夫状态转移模型的问题。

2)从服务提供商的角度出发，考虑到用户服务的频繁迁移会造成系统长期迁移成本超出迁移阈值，运用Lyapunov 优化方法在保证系统长期迁移成本稳定的基础上，最小化用户服务请求的平均感知时延。

3)为降低混合整数非线性规划问题的求解复杂度，设计了一种以用户为中心的异步最佳响应方案来寻找近似最优的边缘服务迁移策略，在显著降低算法运行时间的同时，进一步降低了用户服务请求的平均感知时延。

2 相关工作

针对移动边缘计算网络中动态服务迁移问题，国内外学者均开展了相关的研究。文献[5]根据用户的地理位置及其服务请求类型，考虑服务运行过程中表现出非对称带宽的需求，提出了一种满足多维（存储、计算与通信）约束的联合优化算法，有效解决了多维约束条件下MEC 增强的多蜂窝网络中的服务放置和请求路由问题。文献[6]考虑到边缘服务器的异构性问题，以最大化服务放置奖励为优化目标，提出了一种灵活的服务放置算法。该算法将每个边缘节点看作某一类应用服务器，在每个时隙进行服务放置决策。上述2 种算法无法为正在移动的用户提供无间断服务，严重降低了用户服务质量。文献[7]通过构造多参数马尔可夫决策过程（MDP,Markov decision process）收益函数解决了由于边缘服务器服务范围有限而造成对移动车辆服务中断的问题，改进了单纯基于距离进行服务迁移方案的不足，但在迁移决策中没有对服务提供方的成本开销进行合理地建模与评估。在用户接入节点固定的非重叠覆盖场景下，Ouyang 等[8]考虑到用户的移动性与服务请求到达的不确定性问题，提出了具有概率分布模型的马尔可夫近似算法，通过构建不可约马尔可夫链得到了不同时间段的最优服务迁移策略。但对于多节点覆盖场景，该算法无法做出用户服务请求的节点选择决策。文献[9]提出了云-边-端三层架构模型，在该模型中，每个基站覆盖下的用户首先向本地MEC 服务器请求服务，当本地MEC 服务器没有响应用户的服务需求时，该请求可通过基站路由到远端云服务器。然而，该方法将导致边缘服务器负载不均衡，部分用户服务质量严重下降等问题，此外，该方案忽略了用户的移动性。文献[10]提出了一种基于边缘认知计算（ECC,edge cognitive computing）的动态服务迁移机制，该机制可以根据用户的行为认知快速地进行服务迁移，解决了用户在不同行为下服务质量大幅度波动的问题。但该机制以满足用户个性化服务为目标，忽视了多用户场景中边缘服务器资源有限的情况。文献[11]结合远程加载与重定向技术提出了基于虚拟机的快速服务迁移方法（FSMM,fast service migration method），该方法基于最短距离为用户实现用户服务迁移，具体地，在边缘服务器覆盖范围内的用户均就近接受服务，不在任何边缘服务器覆盖范围内的用户均由远端云服务器提供服务。文献[12]从理论的角度来量化间歇性连接对移动边缘计算的影响，所提间歇性服务迁移方法（ISMM,intermittent service migration method）根据当前网络环境自适应调整用户服务迁移响应间隔，有效降低了用户的平均感知时延。文献[13]将服务迁移问题描述为马尔可夫决策过程，通过用户与服务位置之间的相对距离来获取近似的底层状态空间，然而，该决策模型仅适用于一维服务迁移场景。

综上所述，已有的相关研究主要从3 个方面实现用户的服务迁移。1)假设用户移动路径已知的情况下，对系统资源与服务迁移策略进行联合优化，使系统某一性能（如用户感知时延、系统吞吐量等）达到最优。2)在服务迁移决策过程中，忽略服务迁移所产生的成本开销与用户被多个微基站重叠覆盖的情况，以提高用户服务质量为优化目标。3)假设边缘服务器拥有充足的计算与存储资源，把用户的移动性建模为一维或二维马尔可夫状态转移模型，根据用户在每个时刻所处的环境状态进行边缘服务迁移决策。然而，在实际应用场景中，用户的地理位置具有部分可预测性，对于运动轨迹无法预测的用户，其移动性无法通过马尔可夫状态转移模型进行刻画。其次，已有研究没有从服务提供商的角度考虑如何在保证用户服务质量的前提下，使边缘服务迁移成本开销保持长期稳定。最后，由于移动边缘计算网络的通信资源、计算能力以及存储容量是有限的，忽略对这类资源的合理调度将导致网络无法应对数量呈爆发式增长且服务质量需求日益增高的各类应用请求。

3 系统模型

本文的系统模型如图1 所示，在宏基站（MBS,macro base station）覆盖范围内存在多个小基站（SBS,small base station），其中MEC 增强的SBS 又称为边缘节点（EP,edge point）。考虑到每个小基站覆盖范围内服务请求量的差异性，为节约部署成本，服务请求量相对较小的地区不需要部署边缘服务器，但对于热点区域情况则相反。实际上，非热点区域的服务请求可以通过小基站转发至宏基站，并由宏基站转发到远端云服务器或者周边的边缘服务器。例如：小基站SBS1没有部署边缘服务器，所以用户user1只能通过宏基站向云服务器或者邻近的边缘服务器请求服务。对于没有被小基站覆盖的用户，其服务请求只能通过宏基站转发到云服务器或者边缘服务器。由于用户的移动性或新用户的加入使网络的拓扑结构发生变化，导致用户的服务进程从原来的服务器迁移到另一个服务器。开始时刻，小基站SBS2为用户user2提供服务。一段时间后，用户user2移动到小基站SBS3所覆盖的区域。由于边缘服务器存储资源、计算资源以及通信资源有限，在每个边缘服务器上仅能运行有限的应用服务，小基站SBS3没有可供用户user2服务需求使用的资源，因此用户user2在小基站SBS2的服务配置文件只能通过宏基站迁移到邻近的边缘服务器SBS4，从而实现边缘服务迁移。

在宏基站覆盖范围内部署M个SBS 与I个边缘服务器，用户数量为N+1。令T={0,1,2,…,T}表示时间离散化序列集合，表示用户k在时隙t内关于BSj（j=0 时为MBS，j≠0 时为SBS）的接入参数，用户k接入BSj，则，否则。通常情况下，用户k只能接入到一个BS。因此，对任意的用户k来说，其接入约束条件如式(1)所示。

由于边缘服务器处理任务的输出结果远小于任务大小[14-17]，本文只考虑上行信道资源分配。假设系统的通信资源块（RB,resource block）总数为F，每个通信资源块的带宽为WMHz，宏基站的资源块总数为C0，剩余的F-C0通信资源块由SBS复用。由于不同SBS 所管理的无线资源存在差异性，所以对于任意的SBSj，其占用的无线资源块数应满足Cj≤F-C0，1≤j≤M。因此，对任意的BSj，为保证用户所占用的通信资源在其承受范围内，其通信资源约束条件需满足

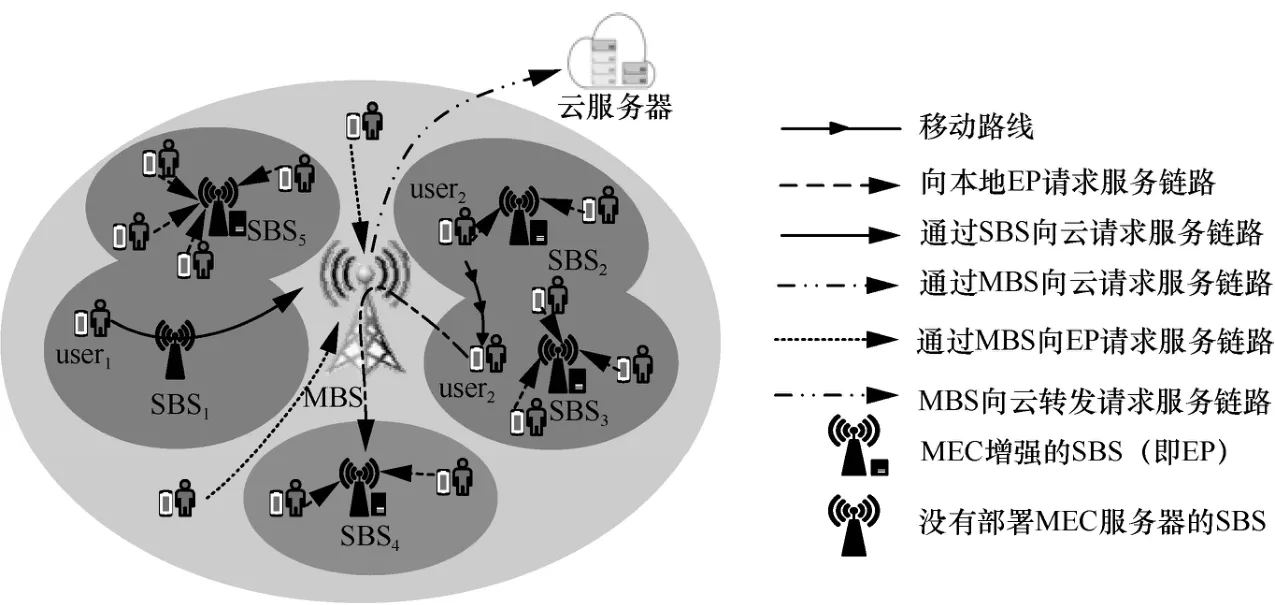
图1 系统模型

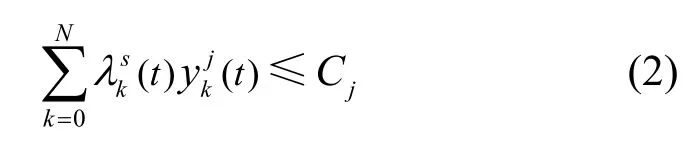
由于服务器计算与存储能力有限，对于任意的时隙t，服务器i服务用户所需的计算与存储不能超过其总的计算与存储资源，因此服务器i的计算资源约束条件如式(3)所示，存储资源约束条件如式(4)所示。

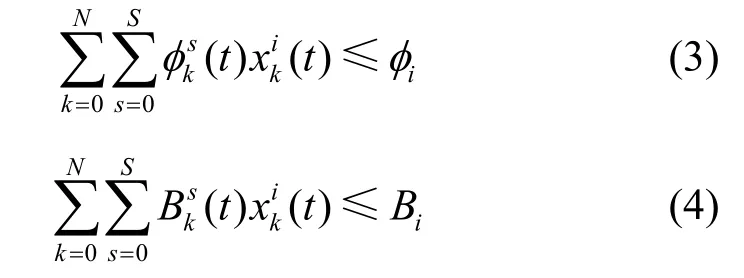
其中，φi和Bi分别表示服务器i的总计算资源与总存储资源；分别表示用户k请求服务s所需要的计算资源与存储资源；S+1 表示所有用户服务请求服务类别的总和；表示用户k被服务器i所托管，i=0 时表示云服务器，否则表示边缘服务器。

3.1 服务体验模型

由于用户发起的服务请求被边缘服务器或者云服务器响应，因此用户的数据传输存在一定的传输时延。在本文模型中，传输时延可分为以下三类：1)用户的服务请求被本地边缘服务器响应；2)用户的服务请求通过MBS 转发到邻近的边缘服务器；3)没有边缘服务器响应用户的服务请求时，该请求只能被远端云服务器响应。因此，系统中所有用户发送服务请求到BS 的传输时延Dc(t)为

MBS 转发服务请求到SBS 或者云服务器的传输时延Df(t)为

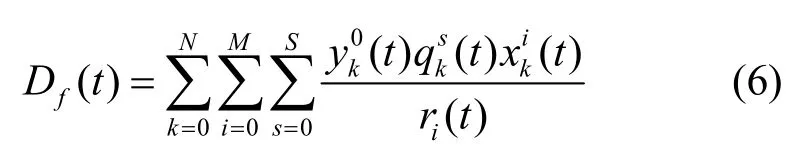
所有用户的服务请求被服务器响应的总时延Dtotal(t)为

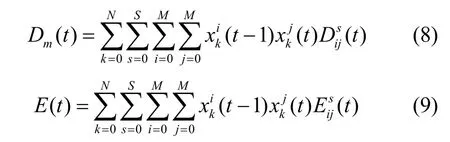
3.2 系统性能与成本

首先，为缓解数据上传到远端云服务器对核心网造成的流量拥塞问题，部署在边缘服务器上的服务应最大化满足用户的需求。其次，为降低网络拓扑结构变化所带来的服务迁移成本，系统中所有用户在时隙t内的服务迁移成本E(t)应保持在预期的范围之内，令Eavg表示长期预算迁移成本，可得成本约束条件如式(10)所示。

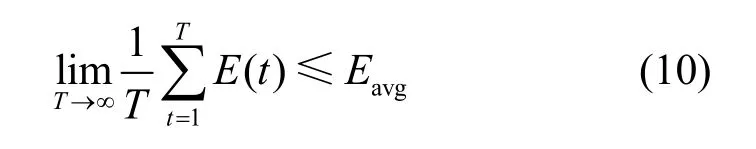
在保证系统长期平均迁移成本小于预算成本的约束条件下，根据用户服务请求制定最优的服务迁移策略，使所有用户的平均感知时延与服务迁移时延之和最小，可得如下优化问题。

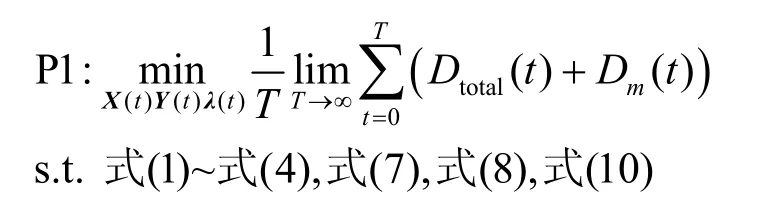
4 基于Lyapunov 优化的在线服务迁移

用户的移动容易造成用户服务在服务器之间频繁迁移，为服务提供商带来高昂的迁移费用。从服务提供商角度考虑，如何在保证服务迁移成本不超出其所能承受阈值的基础上，最大化降低用户所需服务的感知时延是动态服务迁移策略必须满足的关键目标之一。为实现该目标，本文运用Lyapunov 优化方法保证系统的长期迁移成本小于迁移阈值的同时，满足用户对感知时延的要求。Lyapunov 优化的关键思想是在当前用户的感知时延和迁移成本之间取得相对的平衡，通过为长期成本预算引入虚拟队列来保持迁移成本的长期稳定。首先将虚拟队列定义为超出预算成本的历史度量，假设初始队列长度为0 bit（即Q(0)=0 bit），队列更新方式如式(11)所示。

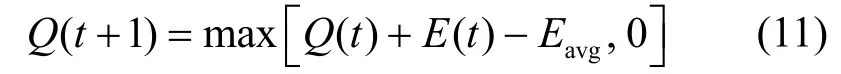
直观上，Q(t)可以作为当前服务迁移成本状况的评价标准。Q(t)越大，表示自实施在线服务迁移策略开始，迁移成本超过长期预算迁移成本Eavg越多。为了保证长期迁移成本低于Eavg，Q(t)必须满足，其中 E[⋅]表示数学期望。

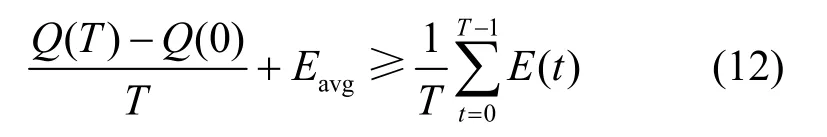
由于Q(0)=0，可进一步得到

式(13)表明了长期迁移成本不能超过预算成本。为了保持虚拟队列稳定，首先分别定义二次Lyapunov 函数与Lyapunov 漂移函数[18-20]如式(14)与式(15)所示。

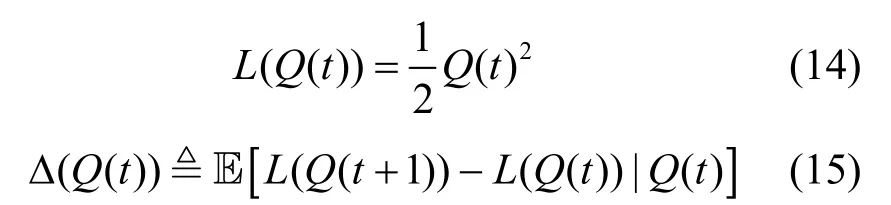
其中，Δ(Q(t))表示在二次Lyapunov 函数中，相邻时隙间迁移成本的变化量，该变化量有助于调整服务迁移策略以适应系统的动态变化。

为了得到当前时隙下最优的服务迁移策略，可通过Lyapunov 优化方法把原始问题分解为实时性优化问题。为保持系虚拟队列稳定，通过定义Lyapunov漂移加惩罚函数构建实时服务迁移问题，其中Lyapunov 漂移加惩罚函数如式(16)所示。

进一步可以得到

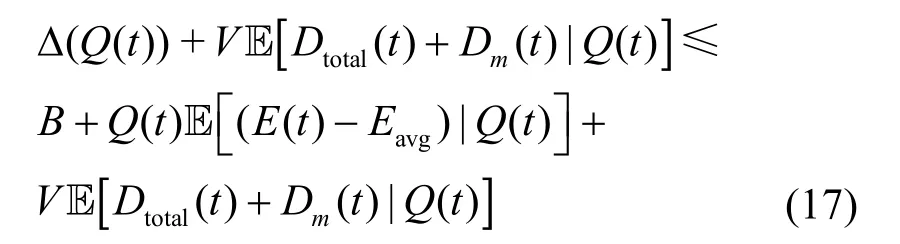
其证明如下。

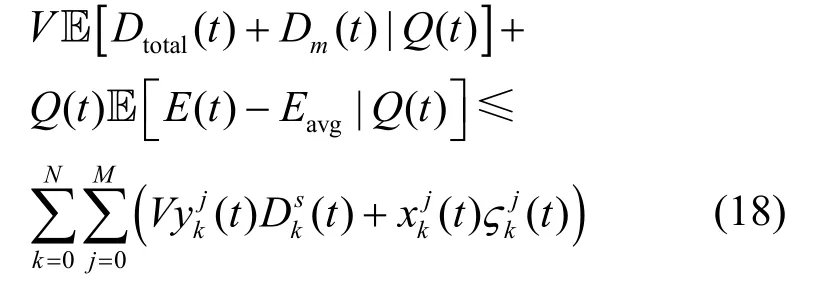
运用Lyapunov 优化将问题P1转化为用户接入节点选择与服务迁移决策的问题P2。对于问题P2 的求解，可使用穷举法列举所有可能的服务迁移策略，然后基于拉格朗日乘子法或者内点法求出当前服务迁移策略下的最优通信资源分配λ(t)。然而，穷举法算法复杂度为O(FNM)，复杂度过高，无法应用于大型移动边缘计算网络。观察问题P2 可知，其优化目标的第一项与用户无线接入节点选择Y(t)和通信资源分配λ(t)相关，第二项表示MBS 转发所有用户的服务请求到边缘服务器或云服务器所需的总时延。

5 自适应最佳响应策略

5.1 快速边缘决策算法

本文求解问题P2 的总体思路如下。首先，假设在t时隙内，用户最优的无线接入节点选择参数为Y*(t)。其次，将问题P2 分解为2 个子问题：通信资源分配问题与边缘节点选择问题。分别求解在已知无线接入策略Y*(t)的情况下最优的λ*(t)和X*(t)。最后，将λ*(t)与X*(t)代入问题P2，求解出最优的Y*(t)。具体地，通信资源分配问题P2_1表述如下。

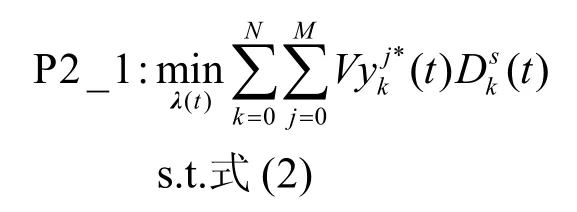
运用拉格朗日乘子法消去约束条件(2)，得到如下优化算子。

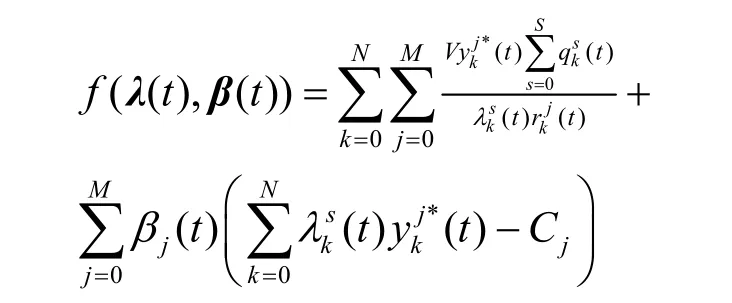
进一步联立式(19)和式(20)，可得

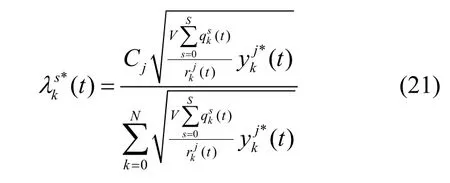
通过式(21)可以求得所有用户的最佳通信资源分配策略λ*(t)。

同理可得，在已知全局最优的无线接入节点选择策略Y*(t)后，服务迁移问题P2_2 表述如下。

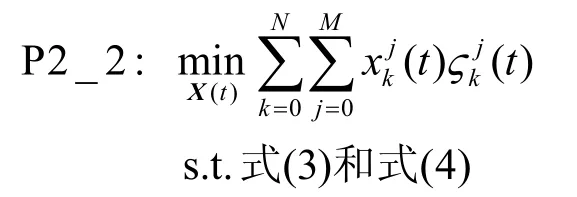
化简问题P2_2，可得

其中，符号.*表示矩阵点乘，符号sum(⋅)表示对矩阵所有元素求和。为减少计算复杂度，本文提出快速边缘决策算法求解最优服务迁移决策参数X(t)，如算法1 所示。

算法1快速边缘决策算法

输入初始化矩阵X(t)=0

输出最优服务迁移策略X*(t)

通过式(21)及算法1 求解X*(t)并化简问题P2，使优化目标只包含决策参数Y*(t)。由于化简后的问题仍是整数非线性规划问题。为在计算复杂度与用户的服务质量之间取得折中，本文进一步提出异步最佳响应算法，以用户为中心，可以为用户快速地选择无线接入节点。

5.2 异步最佳响应更新策略

令U(Y(t))表示问题P2 的效用函数，用y-k={y0,…,yk-1,…,yN}表示除用户k之外，所有用户的边缘节点选择向量。在已知其他用户的边缘节点选择策略情况下，用户k通过选取某一个覆盖该用户的SBS 或者MBS 作为无线接入节点，使U(Y(t))最小化，如式(22)所示。

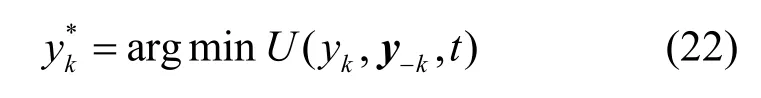
由于上述问题为非合作性的无线接入节点选择问题，存在一个基于博弈论的无线接入策略，使所有用户的接入节点选择达到纳什均衡。因此，当任何用户都无法通过单方面更新其无线接入策略来进一步降低其成本时，所选择的无线接入策略为最优Y*，即对于任意的用户m来说，都有式(23)所示的不等式成立。

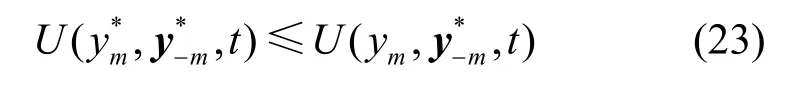
本文根据式(22)与式(23)提出了异步最佳响应算法，其主要流程如下。用户将服务请求发送到初始连接的BS 后，MBS 为其服务请求分配一个唯一编号ID；然后根据分配的ID 顺序更新所有用户的边缘节点选择策略，具体地，对当前还没有更新的最小ID 的用户的服务请求分配一个更好的边缘服务器或云服务器。因此，任意用户k的无线接入节点选择更新流程如式(24)所示。

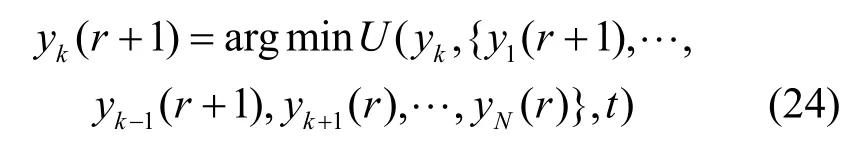
其中，r表示策略更新轮数。在已知当前所有用户的接入策略情况下，比用户k的ID 小的用户根据不等式(24)进行更新，比用户k的ID 大的用户接入策略保持不变。异步最佳响应算法如算法2所示。

算法2异步最佳响应算法

输入初始化,随机为每一个用户服务请求分配一个接入节点，并设置初始迭代轮数r=0

输出Y*

由于用户的随机移动，使用户在每一个时隙之间的地理位置可能不同。通过快速边缘决策算法及异步最佳响应算法求解出每个时隙t的最优的边缘节点与无线接入选择策略，然后不断更新每个时隙的虚拟队列长度，最后得到系统长期服务迁移决策。其流程如算法3 所示。

算法3自适应最佳响应算法（AORAM,adaptive optimal response algorithm）

输入初始化虚拟系统成本队列Q(0)=0

6 数值分析

本文采用Python IDE PyCharm 作为实验的仿真软件，版本为 PyCharm Community Edition 2019.2.5。为缩短仿真时间，使用戴尔易安信PowerEdge R730 机架式服务器（Xeon E5-2603 V3/8 GB/1.2 TB）搭建仿真平台。仿真场景设置如下：在900 m ×900 m区域内部署4 个SBS 和一个MBS，初始用户数M=50。本文采用3 种对比算法，分别为当前最优服务器迁移（COSM,current optimal server migration）、ISMM[12]与FSMM[11]。COSM为一个基准算法，为防止用户频繁进行边缘节点选择，在每个时隙开始阶段，只对位置发生变化的用户进行边缘节点选择，其他用户接入参数保持不变。ISMM 中，每隔一段时间τ0（实验设置为4 s），BS 根据当前时刻T1的用户位置信息进行服务迁移，并在下一个时间段T1-(T1+τ0)内不进行任何服务迁移[12]。FSMM 基本思想为每个边缘服务器只服务其覆盖范围内的用户，无边缘服务器覆盖的用户均由远端云服务器提供服务[11]。

考虑到现实情况中，用户的运动轨迹可以分为确定性运动轨迹与非确定性运动轨迹，例如，用户每天的上下班路径及其所处地理位置可以根据大量的历史数据预测出来，而用户出差或者旅游的运动路径由于数据稀疏性难于预测。本文把用户的运动分为沿着确定轨迹运动与每个时隙的地理位置随机2 种情况。具体仿真参数设置如表1 所示。

6.1 确定性用户轨迹仿真模型

确定性用户轨迹模型如图2 所示，其中，用户user1与user2分别沿着2 个确定的路径轨道运动，其他用户的地理位置保持不变。用户user1与user2完成固定轨迹运动的时间均为T=800 s，在每一个时隙τ=1 s 内运动长度在x轴上的分量为1.125 m，其他用户的坐标位置在t=0 时刻随机分布。

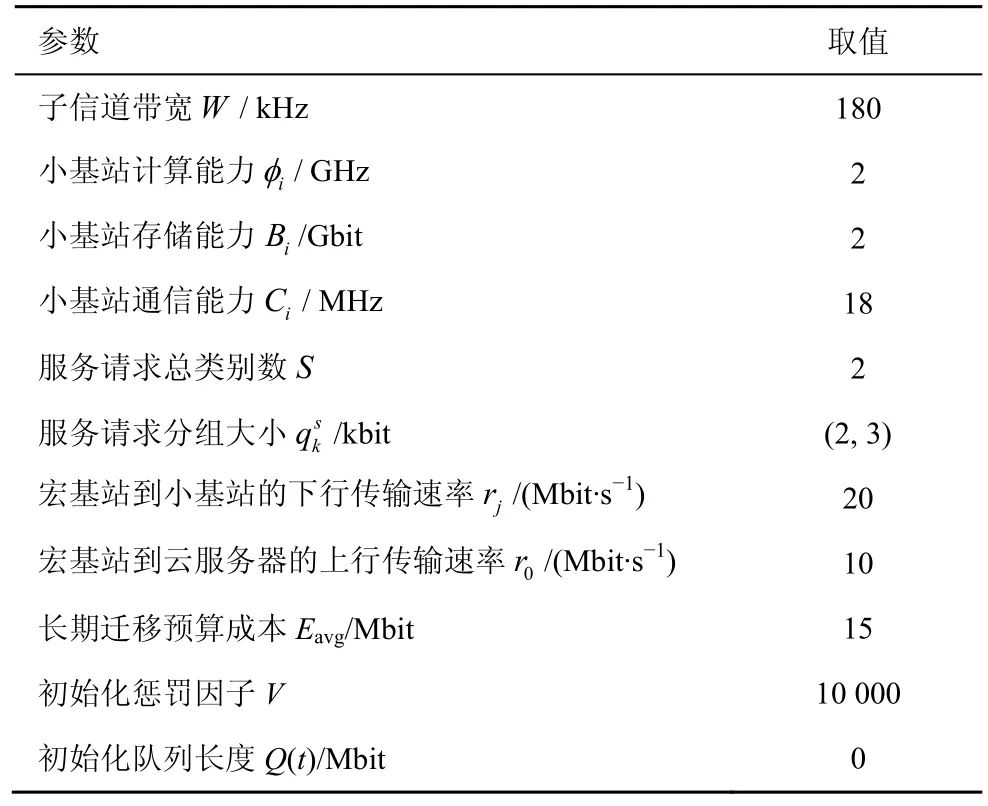
表1 仿真参数

图2 确定性用户轨迹模型

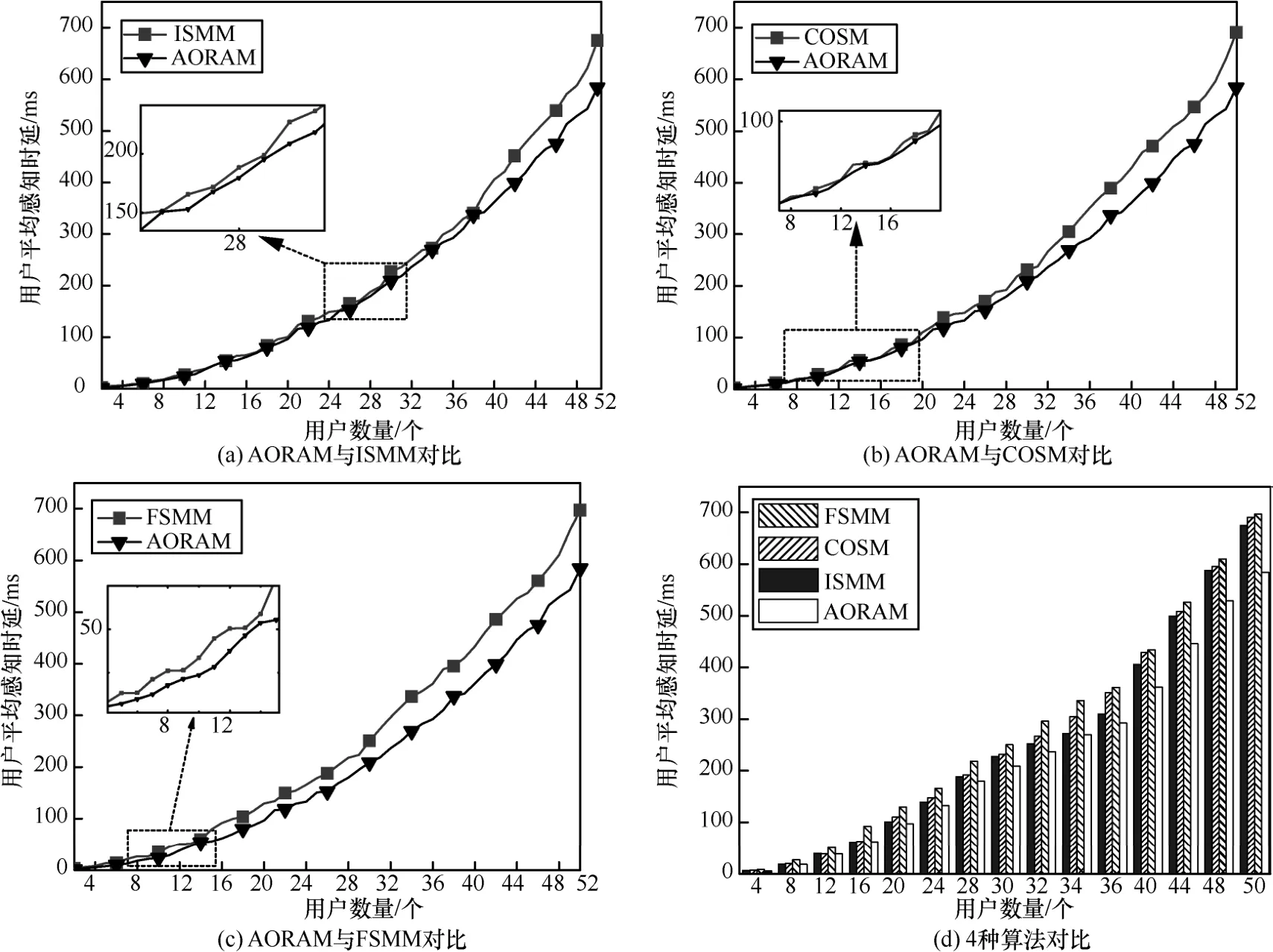
图3 用户的平均感知时延

图3 表示系统用户的平均感知时延。可以看出，本文所提AORAM（即算法3）得到的用户感知时延低于其他3 种对比算法。与AORAM 相比，其他算法均存在用户数量阈值M0，当用户数量M＜M0时，对比算法与所提算法在降低用户感知时延性能方面表现大致相同；但当M≥M0时，随着用户数的增加，AORAM 与对比算法的时延性能差异也随之增大，即所提算法明显优于对比算法。造成上述现象的主要原因在于：当用户数量相对较小时，本地边缘服务器的计算、存储与通信资源充足，能够最快地响应本地用户的服务请求，而当用户数大于某一个阈值时，容易造成某些边缘服务器负载过高，而某些边缘服务器则相反。AORAM 通过转发负载过重的边缘服务器的用户服务到空闲且离用户相对较近的边缘服务器，实现边缘服务器之间的负载均衡，从而降低用户的平均感知时延。此外，分别统计不同用户数量情况下，所提AORAM相对于其他算法的性能增益，并计算平均值。从图3(a)中可以看出，与ISMM 相比，AORAM 能够使用户的平均感知时延降低8.746%，当用户数M≤38时，2 种算法最大差值为36.59 ms，即2 种算法在用户服务质量性能方面表现大致相同，但用户数M＞ 38时，时延差值随着用户数的增加而不断增大。同理可知，在图3(b)中，与COSM 相比，AORAM 能够使用户的平均感知时延降低11.57%，当用户数M≤20时，2 种算法时延差值百分比为10.53%，最大差值为24.68 ms。在图3(c)中，与FSMM 相比，AORAM 能够使用户的平均感知时延降低21.59%，当用户数M≤12时，2 种算法最大差值为40.70 ms。从图3(d)中可以看出，与其他算法相比，所提AORAM 的用户平均感知时延分别降低了8.74%、11.57%、21.59%。显然，AORAM 能有效地降低感知时延，提高用户服务质量。

图4 为4 种算法在不同惩罚因子V情况下虚拟队列长度Q(t)随时间的变化曲线。图 4(a)为AORAM 在不同惩罚因子V下，虚拟队列长度Q(t)的变化情况，可以看出，随着时间推移，虚拟队列长度Q(t)趋于某一个固定值（如当V=500时，虚拟队列长度Q(t)的稳定值为127）。此外，当增大惩罚因子V时，虚拟队列长度Q(t)也随之增大，同时系统达到迁移成本稳定的收敛时间也变长。其原因在于，当增大惩罚因子V时，意味着系统优化目标更偏重于用户的感知时延，导致系统为获取更低的用户感知时延，需要进行更加频繁的服务迁移，从而增加了系统虚拟队列长度Q(t)与达到稳定的时间。也就是说，为提高用户的服务质量，系统需要投入更多的服务迁移成本来换取更高的虚拟队列的积压容忍度。图4(b)为FSMM 在不同惩罚因子V下虚拟队列长度Q(t)的变化情况。当用户user1与user2在如图2 所示的单个SBS 内移动时，其服务迁移决策保持不变，因此虚拟队列长度保持不变；当user1和user2跨SBS 移动时，触发服务迁移策略，其虚拟队长随时间的增长而下降。图4(c)表示COSM 在不同惩罚因子V下虚拟队列长度Q(t)的变化情况。可以看出，随着时间的推移，Q(t)逐渐下降到某一稳定值。图4(d)为ISMM 在不同惩罚因子V下虚拟队列长度Q(t)的变化情况。当V值较小时，每个时刻迁移成本均小于长期迁移阈值Eavg，因此Q(t)值不断变小并最后达到稳定；当V较大时，频繁的服务迁移造成迁移成本大于迁移阈值，使其Q(t)不断增大直到稳定。

图5 为不同惩罚因子V下用户的平均感知时延。可以看出，在平稳状态时，AORAM 得到的用户平均感知时延相对于其他3 种对比算法分别减少了90.84 ms、106.45 ms、112.55 ms。由于FSMM中服务迁移决策取决于用户与SBS 的相对位置，所以V值不影响服务迁移决策，但容易造成边缘服务器负载失衡，导致服务质量降低。当V＜100时，随着V的增加，ISMM、COSM 与AORAM 的感知时延快速下降。但当200≤V＜2000时，AORAM 感知时延能够达到更低值，表明所提的AORAM 在保障更高服务质量的同时增大了长期服务迁移阈值的可调范围。图6 表示不同惩罚因子V下系统的平均迁移成本。虽然AORAM 相比于其他算法具有较高的迁移成本，但其迁移成本随着V值增大逐渐收敛，收敛值仍低于预期阈值Eavg，结合图5 可知，AORAM 在保持系统迁移成本相对稳定的情况下能够显著降低用户平均感知时延。

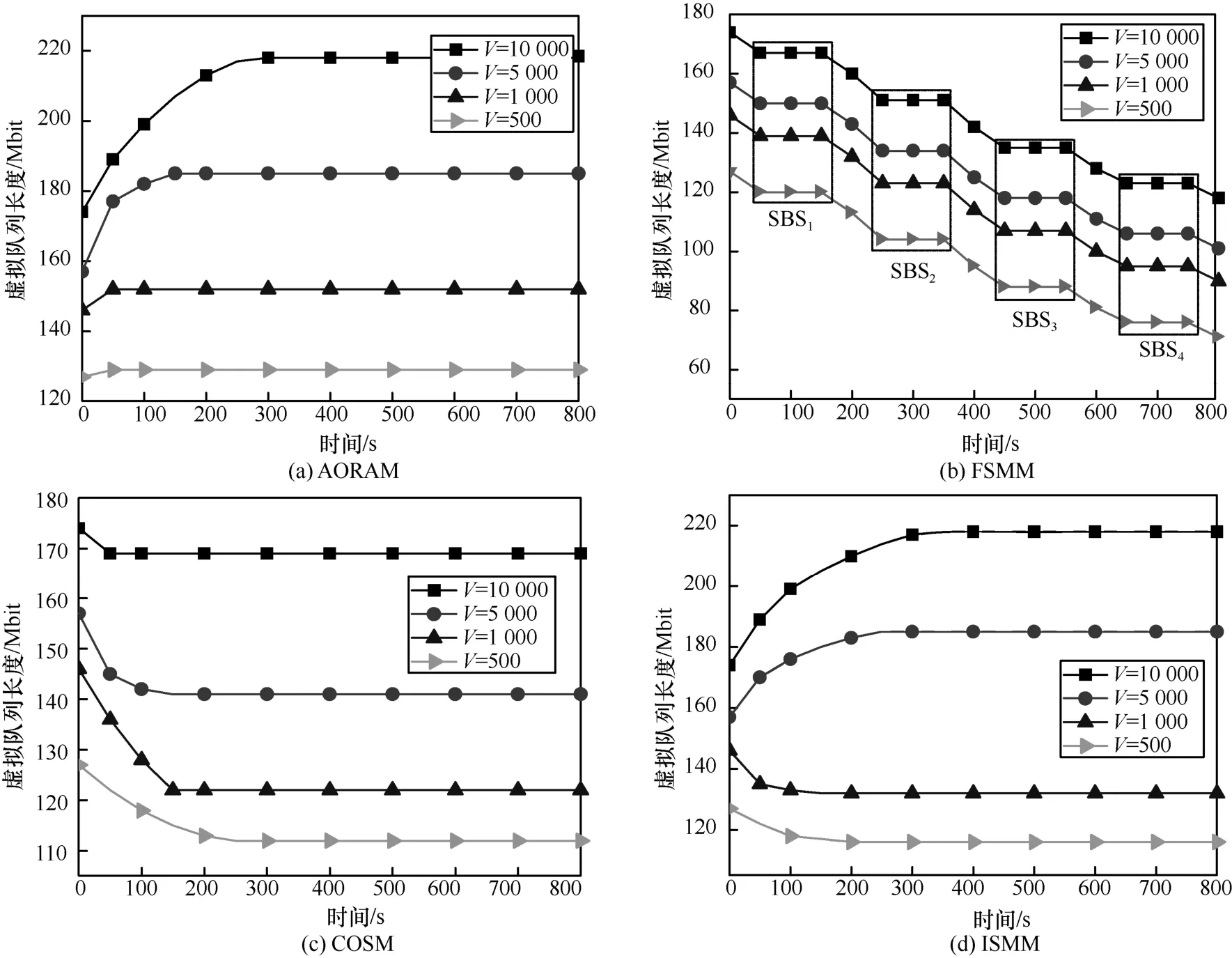
图4 不同惩罚因子V下的虚拟队列长度

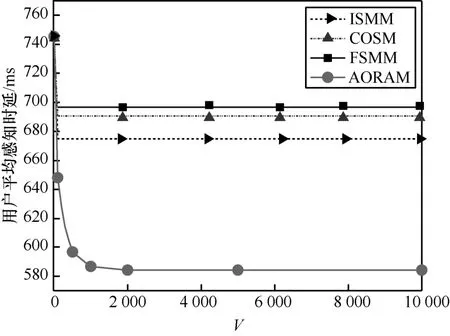
图5 用户感知时延

图6 平均迁移成本

图7 展示了不同长期迁移预算成本Eavg下虚拟队列的长度变化情况，其中M=20 。当Eavg＜15 时，虚拟队列长度随着时间的推移不断增大，无法收敛。根据式(11)可知，过小的Eavg将导致每个时隙迁移成本超出预期，使虚拟队列长度不断增大，出现虚拟队列长度随时间推移而无法收敛的情况。同理，当Eavg为15～25 时，虚拟队列长度最终都随着时间的推移而收敛，且Eavg越大，收敛速度越快，收敛值越小。但是，过大的Eavg导致每个时隙的服务迁移成本都小于长期预算成本，如Eavg=50，根据式(11)可知，虚拟队列长度急剧下降为0。

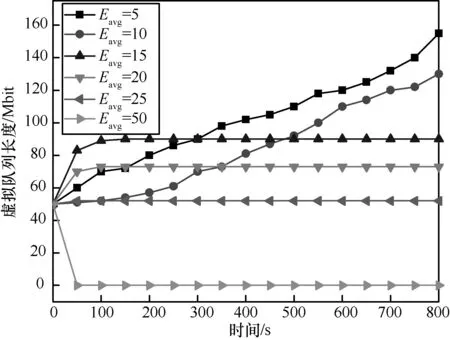
图7 不同长期预算成本下的虚拟队列长度

6.2 非确定性用户轨迹的仿真模型

由于用户的运动路径具有不可预测性，因此在每个时隙t的开始时刻，用户的地理位置表现出随机性。为仿真该情形，在每一个时隙对系统中15 个用户的地理位置进行随机化处理来代表用户的位置变化。对3 000 个时隙进行了仿真，其中在每个时隙的开始时刻对用户的地理位置进行随机初始化处理，惩罚因子设置为V=10 000，迁移预算成本设置为Eavg=35。图8 展示了该场景下虚拟队列长度随时间的变化情况。当所有用户进行随机运动时，前一时刻所得到的边缘节点参数需全部更新为此时刻初始边缘节点参数，即COSM 与AORAM 算法相同。

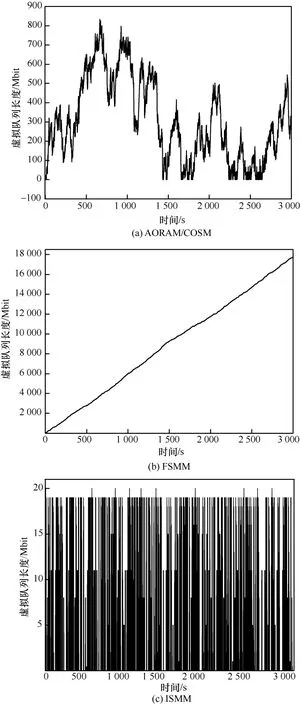
图8 虚拟队列长度随时间的变化

从图8(a)可以看出，当系统中所有用户进行无规则运动时，AORAM 和COSM 得到的虚拟队列长度在0～850 Mbit 之间波动。由于用户位置的随机性可能导致一段时间内大部分用户的位置没有大的变化，出现服务迁移成本低于迁移阈值的情况，根据式(11)可知，虚拟队列长度将会一直处于下降状态直到为0。同理可得，造成虚拟队列长度接近850 Mbit的原因在于，在一段时间内用户在每个时隙内的服务迁移成本一直大于迁移阈值，导致虚拟队列长度一直处于上升阶段。由图8(b)可以看出，当用户进行随机移动时，FSMM 的虚拟队列长度随着时间的推移不断增大，这表明长期迁移成本大于迁移阈值。从图8(c)可以看出，由于ISMM 要求系统每隔一段时间后进行服务迁移，导致虚拟队列长度出现为0 的时间段占总时间的比例达83.97%。通过分析可知，当用户进行无规则随机运动时，系统存在最小的迁移成本阈值，如果迁移预算成本Eavg大于该阈值，随着时间不断推移，虚拟队列长度将在某一范围内不断波动，相反，虚拟队列将不断增大，无法收敛。在这种情况下，用户的服务质量将严重失衡，例如，距离SBS 更近的用户的服务质量更好，但距离SBS远的用户服务质量较差。过大的Eavg虽然能大幅度降低虚拟队列长度，提高用户的服务质量，但增加了服务提供商的服务迁移费用。

用户平均感知时延如表2 所示。从表2 可以看出，相比于FSMM 与ISMM，所提算法能够分别降低用户感知时延18.45%、5.28%。

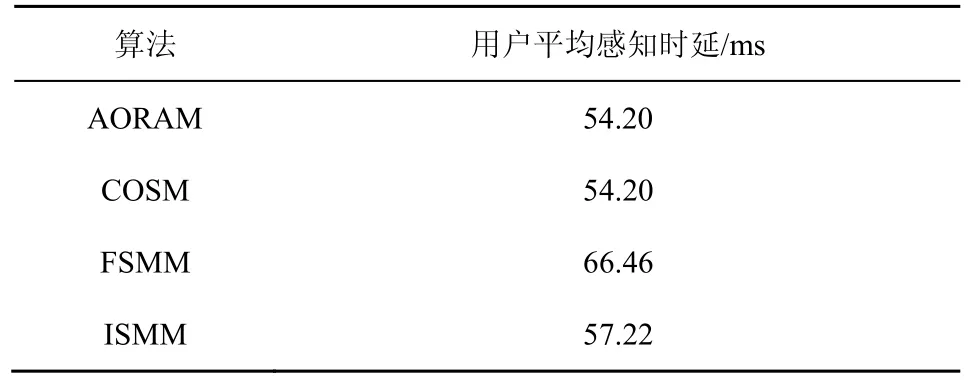
表2 用户平均感知时延

图9 表示所提快速边缘决策算法（算法1）与穷举法在不同惩罚因子V下的虚拟队列长度值。可以观察到，当惩罚因子V＜3 000时，基于2 种算法的虚拟队列长度曲线重合，表明了所提算法与穷举法所做出的服务迁移策略X(t)一致。当惩罚因子V＞3 000时，不同的服务迁移算法所得到的系统性能出现差异，其主要原因在于，随着V值不断增大，系统通过放宽虚拟队列长度的容忍度，进行更好的服务迁移来进一步提高用户服务质量。另一方面，增大V值意味着P2 优化目标更加偏重于用户的感知时延。通过计算得到所提算法与穷举法的平均虚拟队列误差值σ≈3.75%。为进一步验证所提出的算法与穷举法在用户服务质量上的增益差异，仿真了不同用户数下2 种算法的运行时间，如图10 所示。可以看出，随着用户数的增加，2 种算法所需的平均运行时间也随之变大，所提算法在运行时间上远低于穷举法。

图9 平均虚拟队列长度

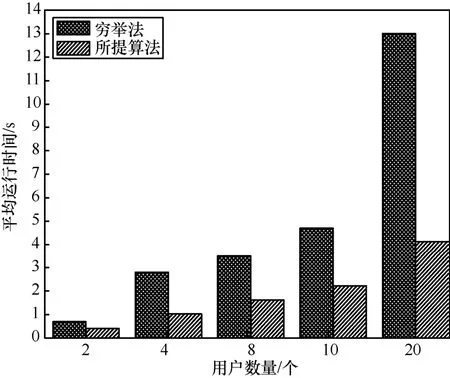
图10 平均运行时间

7 结束语

本文研究了移动边缘计算网络中用户的移动性及其位置的动态性对用户服务请求的平均感知时延的影响，提出了一种移动性感知的在线边缘服务迁移算法。由于优化问题属于高度耦合时间与空间相关性的混合整数非线性规划问题，首先基于Lyapunov 方法将优化问题解耦为边缘服务迁移与节点选择问题，其次提出快速边缘决策算法求解给定边缘节点选择策略下最优的资源分配与服务迁移策略，最后利用所提的异步最佳响应算法求解最优边缘节点选择策略。仿真结果表明，所提边缘服务迁移策略能够有效地降低用户服务请求的平均感知时延。本文方案为移动场景下在线服务迁移的研究提供了新的思路，然而在实际场景中，还需要考虑诸如服务类型、服务请求的最大容忍时延等因素，未来工作将探索上述因素对在线服务迁移性能的影响，为实际网络提供更加准确的决策。