云科学工作流中任务可完成性预测方法

吴修国 苏 玮

(山东财经大学网络与信息安全系 济南 250014) (xiuguosd@163.com)

科学工作流是自动或半自动地求解复杂科研问题的过程，是工作流技术在科学研究上的应用.随着问题求解规模的不断扩大，当今大型科学工作流通常需要在复杂的分布式计算机系统上执行，例如超级计算机、分布式集群系统以及网格系统等[1].然而，构造这样的系统往往需要付出异常昂贵的代价，申请访问这些系统也需要复杂耗时的过程.云计算技术的灵活、弹性、可定制的特点为解决科学工作流运行过程中遇到的问题提供了新思路[2].云科学工作流(cloud scientific workflow)通过云计算平台提供的各种资源与服务部署和执行科学工作流，以低廉的成本为不同地域的研究学者实现资源共享与合作研究提供了一个良好的协作契机[3-4].参照国际工作流联盟(WfMC)的工作流模型定义，云科学工作流系统结构模型由云工作流引擎、服务云、云服务管理机以及用户接口4部分组成，其中，云工作流引擎负责创建协同服务流程、搭建协同服务执行网络以及管理流程执行过程，是实现云科学工作流系统的核心[5-6].

作为一种数据密集型应用，云科学工作流任务往往需要处理大量数据，为使科学工作流的多个子任务可以并行执行，数据被放置在不同的数据中心，任务执行时需要频繁跨数据中心进行数据传输和访问；而在动态分布式环境下，数据中心以及网络等失效事件的发生具有不确定性[7].因此，如何确保云科学工作流任务的高效执行一直是科学计算领域和分布计算领域共同面临的热点和难点问题之一[8-9].通常情况下，云科学工作流任务在启动之前，并不能确定任务所需数据是否可用，从而对工作流任务的完成情况未知.由此，一旦启动云科学工作流任务，可能会由于部分数据不能访问导致任务执行中断.理想的情况是，任务启动前事先对输入数据的可用性情况进行分析，如果发现所有的输入数据都是可用的，那么可以推测：任务启动后，预先设定的任务完成的可能性较高；相反地，如果启动前就发现某些数据是不可用的，或者不能由其他数据生成，这时如果启动了云科学工作流任务，其执行过程很可能会中断，从而导致整个任务被挂起.云计算作为一种按需付费的计算模式，用户使用云计算资源需要支付一定的费用.一旦任务被挂起，不仅造成经济损失，还会使科学工作流运行过程滞后，甚至会影响到科学研究的进度[10].因此，云科学工作流对任务可完成性预测提出了很高的要求.

应该认识到，对一个科学工作流任务可完成性的判定是一项非常复杂的工作，这是因为工作流任务执行处于一个动态变化的云计算环境，任务所需的数据除了系统中已有的原始数据，还包括其他任务执行时计算产生的中间数据；而中间数据的生成又有可能来自于一个或者多个其他的原始数据或者中间数据.任务所需数据的可用性是预测任务可完成性的重要基础；但是直接对输入数据进行可用性判断是不够的，还需要对产生该数据的原始数据进行分析.除此之外，云科学工作流任务执行过程中生成的中间数据，又在某种程度上反映了原始数据的可用性.所以，某一数据可用性可能与其他数据的可用性存在相互影响与相互制约的关系.云科学工作流任务的成功执行对提高云科学工作流系统效率具有重要意义；而数据的可用性是工作流任务成功执行的关键要素[11].基于上述分析，本文提出一种云计算环境下科学工作流任务可完成性预测方法，主要贡献包括3个方面：

1) 从定性和定量2个方面对数据可用性以及数据间可用性相互支持/抑制关系建模，并提出数据可用性更新算法；

2) 基于任务的输入数据可用性分析，提出任务可完成性预测方法，在云科学工作流任务启动前即可对其可完成性进行评估；

3) 应用不同数据集的实验结果表明：基于数据可用性/不可用性的任务可完成性预测方法可以有效提高对云科学工作流任务可完成性情况的认知，从而验证了算法的有效性.

1 相关工作

在云计算环境中，受到网络、设备以及大量产生的劣质数据的影响，云科学工作流的任务可完成性预测是一个非常重要且富有挑战性的问题.目前相关的研究主要是通过不同的任务调度策略，提升云科学工作流系统的效率.比如文献[12]提出了一种云平台下基于相关度的2阶段高效数据放置策略，将任务调度到数据依赖最大的数据中心执行，以减少跨数据中心科学工作流执行时的数据传输量.然而，该策略仅考虑了有关原始数据的可用性；同时，对每个工作流都要进行数据布局与任务调度，势必增加系统负担，导致科学工作流的执行效率反而下降.文献[13]针对跨数据中心数据传输、数据依赖关系和全局负载均衡3个目标，提出了3阶段数据布局策略，对数据布局方案进行求解和优化.但是，云计算环境中的数据往往位于不同的数据中心，无论在构建阶段还是执行阶段，在任务所需数据的可用性未知的情况下，对云计算环境下的数据进行密集型应用是不现实的.文献[14]引入局部关键路径算法思想，提出基于代价驱动的科学工作流调度策略.然而，该方法并没有解决任务可完成性预测问题，也没有考虑调度对任务完成率提升的影响.文献[15]针对传统自适应惯性权重的粒子群任务调度算法容易陷入局部最优，导致调度方案的执行时间与费用较高的问题，提出了一种新的自适应惯性权重计算方法NAIWPSO，以获得执行费用更优的调度方案.该算法着重在提高调度的效率，对调度前后任务的完成情况涉及较少.副本也是云计算环境下提高数据可用性重要手段之一，通过在不同的数据中心复制副本，在降低网络传输时间的同时，提高了数据可靠性与可用性[16].然而，过多的数据副本不仅会带来系统存储、更新等开销，而且多副本带来的不一致性对数据的可用性提出了更高的要求.

一般来说，数据可用性是指数据满足一致性、精确性、完整性、时效性和实体同一性这5个特征的程度[17]；许多学者从上述可用性特征出发进行研究，比如文献[18]针对并行任务调度，通过感知任务“可用性需求”和计算资源“可用性保障”，提出了2种可用性感知的调度算法Afsa和Agsa，提高了任务调度的成功率；文献[19]通过引入资源可用性模型，提出了一种用于维护可用性信息的方法；文献[20]从已有的一致性维护方法出发，对一致性维护过程中所涉及的更新发布、更新传播方式、更新传播内容、更新冲突解决等几个方面进行了分析，提出了相应的解决办法；文献[21]研究了包含冗余记录的集合在给定时效约束下的时效性判定问题，并首次提出了时效性判定问题的求解算法；为提升云平台的数据可用性；文献[22]设计并实现一种虚拟化故障检测恢复系统.在本文中，数据可用性是指数据是有效地、可访问地.上述文献从不同侧面提出了提高任务可完成性的策略，但是大都以孤立的单一数据作为研究对象，既没有考虑数据之间的生成关系，也没有考虑数据之间可用性影响.如何保证具有关联关系的数据在云计算环境中的可用性研究并不多，尤其是针对云科学工作流中中间数据可用性感知方面的研究较少，缺少具体的分析方法.文献[23]从目标之间相互支持/抑制的角度提出了一种目标可满足性推理方法，对本文的研究具有借鉴意义.

综上，从云科学工作流任务执行所需数据出发，基于数据间生成关系，提出数据可用性支持/抑制关系模型；之后，基于数据可用性/不可用性关系传递规则，给出数据可用性/不可用性更新算法，并提出基于数据可用性的任务可完成性预测方法，以此在云科学工作流任务启动之前预判任务的完成性情况，从而提高对云科学工作流任务执行情况的认知.

2 相关模型及问题定义

本节给出云科学工作流中任务、数据、数据生成关系及数据间可用性关系模型，并引入带可用性支持度的数据生成关系图.

2.1 任务以及数据生成关系模型

在云科学工作流中，任务是指为实现某一业务目标而组合起来的数据、流程等.

定义1. 任务.任务t可以描述为一个五元组形式(ti d，Gt，TL，Din，Dout)，其中：

1)ti d是工作流任务标识，具有唯一性；

2)Gt是云科学工作流业务目标描述；

3)TL=({st1，din1，R1，dout1，st2，din2，R2，dout2，…，}，Schedule)是工作流任务说明书，包括2部分：任务列表{st1，din1，R1，dout1，st2，din2，R2，dout2，…，}和任务调度Schedule；Ri是子任务sti的资源需求，i∈{1，2，…，n}；

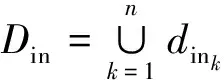
云计算环境下，数据存储在相对独立的云数据中心；数据中心通过网络建立连接.不失一般性，这里的数据是一个抽象概念，指具有完整意义的信息实体，既可以是文件系统中一个有一定独立信息的文件，也可以是存储系统中的一个对象.设数据集合为D={d1,d2,…,dn}.

云科学工作流环境中，依据数据的来源，可以将数据分为原始数据和生成数据2种形式，即dtype∈{T_ori，T_gen}，其中，T_ori为原始数据集，主要指作为流程应用的初始数据，是科学工作流进行数据分析和处理的基础，其存储位置相对固定，一旦被删除将不能被恢复.T_gen为生成数据集或者中间数据集，指由原始数据集经过一次或多次计算产生的中间或者最终数据，其存储位置可以灵活存放，如果已知数据的生成过程也可重新生成.

定义2. 生成关系.设有生成数据di和dj，如果dj(也可能联合其他的数据dk)可经过计算得到数据di，则称数据di和dj之间具有生成关系，记为dj→di.

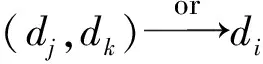
定义3. 数据生成关系图.数据生成关系图G可以描述为三元组(VD，ED，φ)，其中：

1)VD是数据节点的集合，它对应于一个数据(原始数据或者生成数据)；

2)ED是连接边的集合，边e=(di，dj)∈ED当且仅当数据di可由dj是生成；

3)φ是VD上2个或多个节点到{and，or}上的关系映射，其中，and表示“与”关系，在关系图中用连接弧表示；or表示“或”关系，在关系图中用箭头表示.

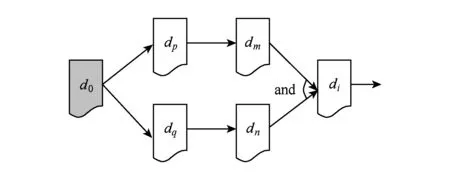
Fig. 1 Data generation relation graph图1 数据生成关系图

利用数据之间的生成关系，可以构造出数据生成关系图G，具体构造方法如下：

1) 将任意的数据di映射为图G中的点vi；

2) 如果数据di，dj之间存在生成关系，则在图中添加由vi到vj的有向边；

3) 依据数据生成的{and，or}关系，添加连接弧.

2.2 带可用性支持度的数据生成关系图

数据之间的生成关系描述了数据的来源.在实际应用中，数据之间往往还存在着相互影响与相互制约的关系.举例来说，假设数据di表示通过计算得到的某一数据集的均值；数据dj表示的是对同一数据集求其得的方差，如果当前数据di可经过计算获得，说明其原始数据集是可用的.同时，从另一方面来说，数据di的正确获取，在很大程度上能够支持数据dj正确获取的可能性，即数据di的可用性对数据dj的可用性起正向支持作用.再比如说，数据dk和数据dm被放置在同一个数据中心上存储，硬件可靠性、网络可靠性、传输效率等相同，如果目前有证据表明数据dk是不可用的，显然，dm的不可用的可能性相当高.像这种广泛存在于数据间的数据可用性相互影响、相互制约的关系，称之为可用性支持度.

一般来说，可以将数据间的可用性支持度分为4种类型：可用性支持、可用性抑制、不可用性支持和不可用性抑制，分别用+s，-s，+d和-d表示.

在数据生成关系图的基础上，增加数据之间的可用度支持关系即可得到带数据可用性支持度的数据生成关系图.

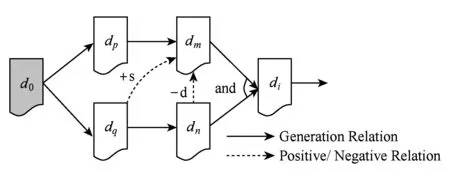
Fig. 2 Data generation graph with support degree图2 带数据可用性支持度的数据生成图

定义4. 带数据可用性支持度的数据生成关系图.带数据可用性支持度的数据生成关系图G*是一个四元组(VD，ED，φ，ω)，其中，VD，ED，φ与定义3中的含义相同；ω是定义在VD上2个数据组成的数据对到{+s，-s，+d，-d}的可用性支持/抑制映射关系.

图2给出了带数据可用性支持度的数据生成关系图.

3 数据可用性的定性描述与推理

为描述数据可用性及其推理关系，本节引入数据可用性定性描述模型，并描述数据间可用性/不可用性传递关系.

3.1 数据可用性模型

在生成关系基础上，进一步地，可以用4个谓词描述对数据di的可用性认知，即FS(di)，FD(di)，PS(di)，PD(di).

1)FS(di)：数据di一定是可用的(存在足够的证据表明数据di的可用性)；

2)PS(di)：数据di可能是可用的(存在部分证据表明数据di的可用性)；

3)FD(di)：数据di一定是不可用的(存在足够的证据表明数据di的不可用性)；

4)PD(di)：数据di可能是不可用的(存在部分证据表明di不可用).

为了能更加直观地说明数据间的可用性关系，引入蕴含算子“⟹”.P⟹Q当且仅当由条件谓词定义的谓词公式“P→Q”是一个永真式(重言式).

显然，对同一个数据di满足2个公理：

公理1.FS(di)⟹PS(di).

公理2.FD(di)⟹PD(di).

结合前面数据间的生成关系、数据间可用性描述以及公理1,2，数据之间的可用性关系存在以下性质.

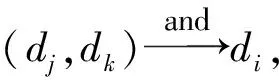
1)FS(dj)∧FS(dk)⟹FS(di).

2)PS(dj)∧PS(dk)⟹PS(di).

3)FD(dj)⟹FD(di);

FD(dk)⟹FD(di).

4)PD(dj)⟹PD(di)；

PD(dk)⟹PD(di).

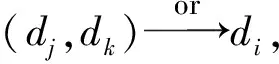
1)FS(dj)⟹FS(di)；

FS(dk)⟹FS(di).

2)PS(dj)⟹PS(di)；

PS(dk)⟹PS(di).

3)FD(dj)∧FD(dk)⟹FD(di).

4)PD(dj)∧PD(dk)⟹PD(di).

性质3. 数据di和dj的可用性关系：

3.2 数据间可用性不可用性定性推理规则

为进一步描述数据间可用性/不可用性传递关系，引入模糊谓词Ava(di)和模糊谓词Una(di)以度量数据的可用性情况.谓词Ava(di)和谓词Una(di)分别表示对数据di的可用性和不可用性的定性评价，并将数据di的可用性/不可用性程度划分为3个等级{F，P，N}，其中F表示“完全”，P表示“部分”，N表示“未知”，并约定F>P>N.由此，模糊谓词Ava(di)和模糊谓词Una(di)可视作一个可比较大小值的三值逻辑.

基于模糊谓词Ava(di)和模糊谓词Una(di)的数据可用性/不可用性解释如下：

1)Ava(di)=F表示有充足的证据表明数据di是可用的.

2)Ava(di)=P表示有部分证据表明数据di是可用的.

3)Ava(di)=N表示数据di可用性未知.

4)Una(di)=F表示有充足的证据表明数据di是不可用的.

5)Una(di)=P表示有部分证据表明数据di是不可用的.

6)Una(di)=N表示数据di不可用性未知.

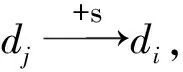
1) 如果Ava(dj)=N，那么Ava(di)=N；

2) 如果Ava(dj)=P，那么Ava(di)=P；

3) 如果Ava(dj)=F，那么Ava(di)≥P.

基于上述约定和分析，可以得到表1所示的数据可用性/不可用性传递规则.

Table 1 Data Availability and Unavailability Propagation Rules in the Qualitative Reasoning 表1 数据可用性不可用性定性传递规则

Table 1 Data Availability and Unavailability Propagation Rules in the Qualitative Reasoning 表1 数据可用性不可用性定性传递规则

IndexDataRelationAvailabilityAva(di)UnavailabilityUna(di)1(dj，dk)and→dimin(Ava(dj)，Ava(dk))max(Una(dj)，Una(dk))2(dj，dk)or→dimax(Ava(dj)，Ava(dk))min(Una(dj)，Una(dk))3dj+s→dimin(Ava(dj)，P)N4dj-s→diNmin(Ava(dj)，P)5dj+d→diNmin(Una(dj)，P)6dj-d→dimin(Una(dj)，P)N

3.3 数据生成关系图中可用性不可用性更新算法

在云科学工作流管理中，工作流任务往往运行在一个服务动态、多变的环境中，数据可用性也会随着外界环境的变化而不断变化.一旦一个数据的可用性发生变化，可能会对其他数据的可用性认知产生影响，而这会直接关系到对工作流任务的完成情况的预测.比如某些中间数据被删除，或者网络拥塞等，会使得某些数据的不可用性提高，或者可以断定某个数据是不可用的.因此，当某些数据的可用性发生变化时，要及时更新带支持度的数据生成关系图中各数据的可用性.算法1给出了带支持度的数据生成关系图中数据可用性情况更新算法.

算法1. 数据可用性更新算法.

输入：带支持度的数据生成关系图G*=(VD，ED，φ，ω)，数据可用性初始评价值Initial[]；

输出：更新后的数据可用性评价值Current[].

① Begin

②Current[]=Initial[]；/*初始化*/

③ While(Current[]≠Old[]) Do

④Old[]=Current[]；

⑤ 对每一个di∈VDDo

⑥Current[i]=Update_Ava_Una(i，G*，Old)；

⑦ End while

⑧ ReturnCurrent[]；

⑨ End

其中，Update_Ava_Una()是数据可用性/不可用性更新函数.

函数1.Update_Ava_Una(i，G*，Old)

① Begin

③ {Avai j=Apply_Rules_Ava(di，r，

Old)；

④Unai j=Apply_Rules_Una(di，r，

Old)；}

⑤ Return(max(maxj(Avai j)，

Old[i].ava)，max(maxj(Unai j)，

Old[i].una))；

⑥ End

算法1定义了数据结构Initial[]，Current[]和Old[]，它们的值域均为{F，P，N}，分别用来存储数据的初始可用性评价值、当前可用性评价值和前一次可用性评价值，其中Old[]的初始值全为N.Apply_Rules_Ava()指的是应用表1中的可用性传递规则；Apply_Rules_Una()指的是应用表1中的不可用性传递规则.算法开始时，将数组Current[]置为Initial[]，在后面的每一步操作中，数据di的可用性/不可用性属性Ava(di)/Una(di)都会通过函数Update_Ava_Una()得到更新，直到Current[]和Old[]中的值相等，循环结束.

定理1. 给定带支持度的数据生成依赖图G*及其可用性初始值Initial[]，算法1中的循环最多会执行6|VD|+1次，|VD|表示图G*中节点的个数.

证明. 从算法1中的语句⑥以及函数1中语句⑤可以看出，对每一个数据di都有：

Current[i].ava=max(…，Old[i].ava)；
Current[i].una=max(…，Old[i].una).

所以，数据di的可用性/不可用性值是单调非递减的.如果算法没有结束，那么从循环条件(Current[]≠Old[])可知每一次循环至少有一个值会发生变化.关系图G*共有|VD|个数据，每一个数据di有2个属性：ava和una，而他们的可能取值只有3个，即{F，P，N}，所以每一次循环至少有一个值会增加，最多增加3次.因此，算法1最多会执行6|VD|+1次.

证毕.

利用上述数据可用性推理及更新算法，基于数据可用性的任务可完成性以及不可完成性的定性描述如下.

定义5. 设有任务t，则基于数据可用性的任务可完成性定义为Pos_t=min(din1.ava，din2.ava，…，dinn.ava),不可完成性定义为Impos_t=max(din1.una，din2.una，…，dinn.una)，dini∈t.Din，i∈{1，2，…，n}.

4 数据可用性的定量描述与推理

从第3节的分析可以看出，数据之间在可用性方面存在一定程度上的支持/抑制影响，而这种可用性关系究竟会起多大的作用，则需要对它们进行定量分析.

4.1 数据可用性定量描述

类似于3.1节的讨论，为了能够定量地描述数据的可用性，引入模糊谓词Ava(di)和模糊谓词Una(di)，分别用于对数据di的可用性和不可用性程度进行定量度量，其中，0≤Ava(di)≤1，0≤Una(di)≤1.由于Ava(di)和Una(di)的值域是一个实值域，所以它们具有模糊函数的意义.

与数据可用性定性分析一样，数据之间的可用性关系定量分析也具有相似的性质.为此，引入关系运算符⊗和⊕，它们都是[0，1]×[0，1]→[0，1]上的二元函数.对于任意x，y∈[0，1]，运算符定义如下：

1)x⊗y=x×y；

2)x⊕y=x+y-x×y.

显然，运算符定义满足关系：x⊗y≤x，y≤x⊕y.

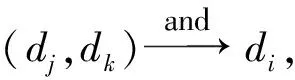
1) (Ava(dj)≥x)∧(Ava(dk)≥y)⟹Ava(di)≥(x⊗y).

2) (Una(dj)≥x)∧(Una(dk)≥y)⟹Una(di)≥(x⊕y).

1) (Ava(dj)≥x)∧(Ava(dk)≥y)⟹Ava(di)≥(x⊕y).

2) (Una(dj)≥x)∧(Una(dk)≥y)⟹Una(di)≥(x⊗y).

性质6. 数据di和dj的可用性关系：

其中，w是权值，可以将其解释为条件概率，即p[di可用/dj可用]，也就是当数据dj可用时di可用的概率.基于上述分析，数据之间的可用性/不可用性定量传递规则如表2所示:

Table 2 Data Availability and Unavailability Propagation Rules in the Quantitative Reasoning

表2 数据可用性不可用性定量传递规则

Table 2 Data Availability and Unavailability Propagation Rules in the Quantitative Reasoning

IndexDataRelationAvailabilityAva(di)UnavailabilityUna(di)1(dj，dk)and→diAva(dj)⊗Ava(dk)Una(dj) Una(dk)2(dj，dk)or→diAva(dj) Ava(dk)Una(dj)⊗Una(dk)3djw+s→diAva(dj)⊗wN4djw-s→diNAva(dj)⊗w5djw+d→diNUna(dj)⊗w6djw-d→diUna(dj)⊗wN

4.2 数据间可用性不可用性定量推理

给定带支持度的数据生成关系图G*及其可用性初始值Initial[]，可以利用算法1对生成关系图中各数据的可用性进行更新.尽管数据可用性状态的度量值(Ava()和Una()的值)均为介于0～1之间的实数，算法1仍然是可终止的.

定理2. 给定带支持度的数据生成关系图G*及其可用性/不可用性初始值(Initial[])，可以利用算法1求得数据di(di∈VD)更新后的可用性/不可用性值，并且算法是可终止的.

① 一个无限序列an是柯西收敛的，当且仅当对于任意选定的正数ε，必存在一个整数N，使得对于任意正整数n(n≥N)都有|an+1-an|<ε；序列an是收敛的当且仅当它是柯西收敛的.

证明. 和定理1一样，数据di的可用性/不可用性值是单调非递减的.算法1中的循环终止条件Current[]=Old[]，可以变换为形式：

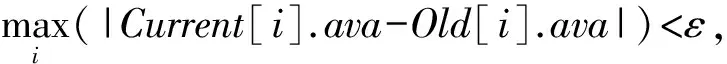
其中,ε是一个无限趋向于0的实数.由于di.ava和di.una的上界是恒定的常数1.所以，序列Current[i]k.ava和Current[i]k.una都是收敛的(柯西收敛准则)①.因此，算法1经过有限次循环之后会终止.

证毕.

由此，与定义5相似，可得基于数据可用性的任务可完成性以及不可完成性的定量描述，用数据可用性的定量值替换其中的定性值即可.

5 实验分析

本节首先给出实验环境,然后进行仿真实验并分析实验结果.

5.1 实验环境

为测试基于数据可用性的云科学工作流任务可完成性预测方法的有效性，在本单位云计算实验室的仿真环境中进行实验.该实验环境参照了澳大利亚斯文本科技大学信息与通讯学院的SwinDeW-C[5-7]体系结构开发而成，其上安装了VMWare②用于数据存储服务；在数据中心部署了Hadoop③用于MapReduce系统开发与数据管理；其硬件配置为：Inter®CoreTMi5-3210M 2.5 GHz；RAM 4 GB；硬盘8 TB；100 MB网络带宽.仿真软件在CloudSim[24]的基础上进行了扩展开发，每个数据中心存放的原始数据个数为50～200个不等，数据大小规模为10～20 GB.每个任务所包含的输入数据个数为10～100个.本文采用模拟的、可定制的科学工作流来测试基于数据可用性的任务可完成性预测方法的有效性，通过分别改变科学工作流的输入数据和任务的数量来控制科学工作流的复杂度.实验过程中，为了保证结果的可靠性，每一个科学工作流在保持配置和云平台环境不变的情况下，运行100次后取平均值作为测试结果.最后，以成功执行的工作流任务比率与本文提出的数据可用性模型预测的比率作为评价指标进行比较，并分析实验结果.

5.2 实验结果及分析

仿真实验1主要是比较工作流任务可完成性与数据可用性之间的关系，即基于数据可用性的任务可完成性判定的可行性问题.图3给出了不同工作流数目下，工作流任务实际完成率与数据可用率关系图.从图3中可以看出，在不同的工作流数目下，任务的完成率与数据可用率变化趋势相似，反映了任务可完成性与数据可用性的密切关系；同时，任务的完成率略低于数据可用率的原因在于除了数据可用性之外，任务完成还受到数据中心、网络等因素的影响.

Fig. 3 Relationship between cloud scientific task completion and data availability图3 任务可完成性与数据可用性之间的关系

仿真实验2主要是从定性角度对工作流任务启动的预测结果与实际执行结果进行比较.实验时，工作流任务包含不同数据个数(Cnt)分别是20，50，80，预测任务可完成是指数据可用性为F或P的比率.图4给出了云科学工作流任务成功执行比率与定性预测比率比较.

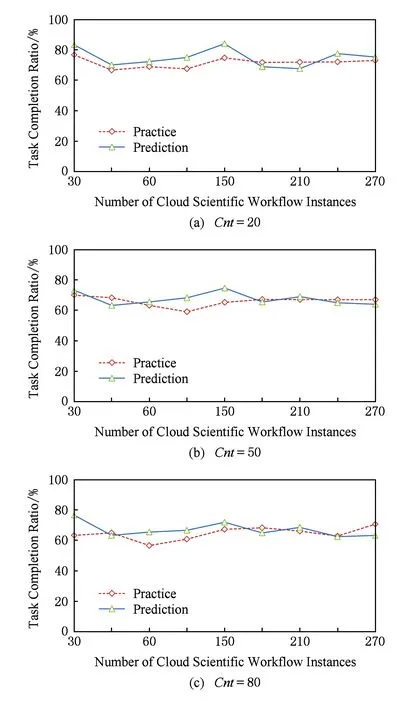
Fig. 4 Comparisons of cloud scientific workflow tasks completion ratio and qualitative prediction ratio图4 任务成功执行比率与定性预测比率比较

整体上看，在不同的工作流数目时，工作流任务成功执行比率与基于数据可用性的预测结果相差不大，并且实际成功执行比率略低于预测值，主要原因是在于图4中考虑的是数据可用性为F或P这2种情况的和，而对于数据可用性情况为P的数据来说，不一定是可用的.而整体执行的效率逐渐降低的原因还在于受到科学工作流规模的影响，随着工作流任务的增加，数据调用频繁，导致整体上数据可用性降低.

仿真实验3主要是从定量角度对工作流任务启动的预测结果与实际执行结果进行比较.类似于实验2，工作流任务包含数据个数分别是20，50，80，预测任务可完成是指数据可用性大于等于60%的任务比率.

图5给出了不同工作流任务数目时成功执行的比率与数据可用性定量预测比率的比较.预测结果以数据可用性大于等于0.6作为任务可完成的标准。从图5(b)中可以看出，当包含数据为50且工作流任务数为210时，预测成功的概率与实际执行的概率相差不大；在任务数为180时，二者相差稍大，原因在于有些生成数据没有被长期保存，或者在调用时被其他任务占用等，总体上对任务成功执行的认知影响不大.

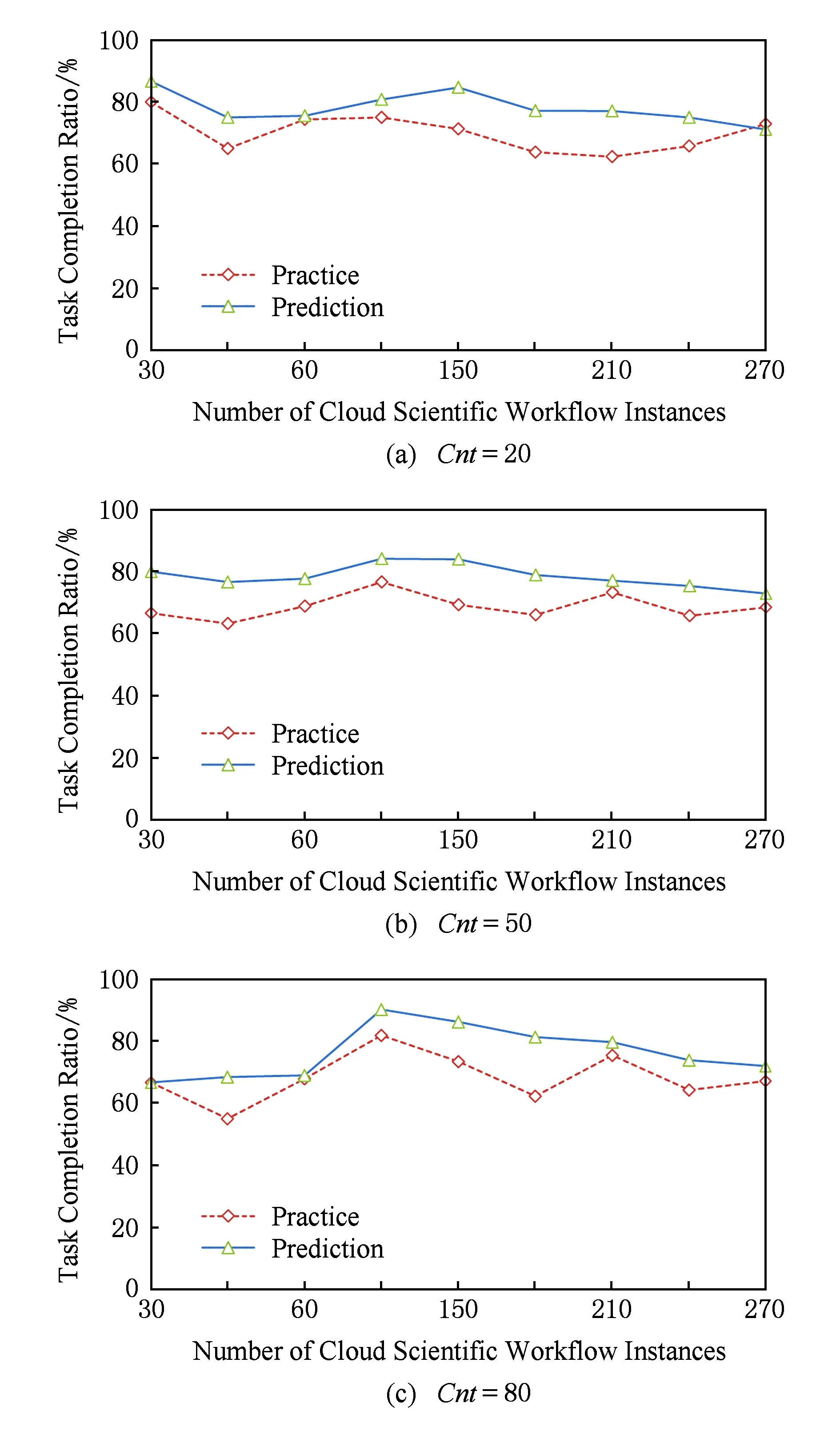
Fig. 5 Comparisons of cloud scientific workflow tasks completion ratio and quantitative prediction ratio图5 任务成功执行比率与定量预测比率比较

Fig. 6 Influence of data storage time with cloud scientific workflow tasks图6 数据驻留时间对云科学工作流任务预测值影响

生成数据在数据中心上的存储时间对任务可完成性预测具有一定影响，仿真实验4测试在不同工作流任务情况下，存储时间分别在1，5，10个单位时间(1h)时，基于数据可用性的任务可完成性预测结果与实际执行结果的比较.结果如图6所示.从图6中可以看出，不同的生成数据驻留时间情况下，任务完成率的预测值之间存在一定差异，随着驻留时间延长，实际值与预测值之间愈来愈接近；而在驻留时间较短时，预测值与实际值差异较大，主要原因是尽管预测的生成数据可用，而实际执行时，生成数据可能会被删除.

实验表明：云科学工作流任务在启动工作流之前，通过对当前环境中各数据可用性分析，在不同的工作流数目与输入数据个数情况下，能够基本预测工作流任务的完成情况，提高了系统的效率.利用该方法，如果数据可用性较高，则可以启动该工作流任务运行；反之，当数据可用性较低时，则需要调整任务，或者等待数据可用性较高时再启动.

6 总 结

云计算环境的动态与开放性、云服务的分布自治性和科学工作流业务逻辑的松散耦合性，使得云科学工作流系统可以充分发挥两者的综合优势；同时，也给云科学工作流任务的可完成性预测提出了更高要求.然而，据我们了解，目前有关云计算环境下科学工作流任务的可完成性预测的研究还非常少.

本文针对云科学工作流环境动态变化、生成数据的可用性更新频繁等特点，提出一种基于数据可用性的工作流任务可完成性预测方法：通过对数据间的可用性支持/抑制关系，分析预测任务的可完成性，尽可能地避免了任务早期的失败对后续任务的影响，从而在工作流任务执行前即可对任务的完成情况有所认知，在有效提升云科学工作流系统执行效率的同时，减少了云计算系统资源的浪费.实验结果表明了该方法的有效性和可靠性，对提高云科学工作流系统性能具有重要意义.未来的研究工作包括：

1) 本文给出的数据可用性/不可用性为静态值，应采用人工神经网络学习等机器学习算法动态修改它们的值，从而提高数据的可用性以及推理的实用性；

2) 本文针对的是单一云科学工作流任务的可完成性预测，还需要对多个工作流任务并行执行时的任务可完成性预测进行研究.

[1] Deldari A, Naghibzadeh M, Abrishami S. CCA: A deadline-constrained workflow scheduling algorithm for multicore resources on the cloud[J]. Journal of Supercomputing, 2016, 73(2): 756-781

[3] Zhang Weimin, Liu Cancan, Luo Zhigang. A review on scientific workflows[J]. Journal of National University of Defense Technology, 2011, 33(3): 56-65 (in Chinese)

(张卫民, 刘灿灿, 骆志刚. 科学工作流技术研究综述[J]. 国防科技大学学报, 2011, 33(3): 56-65)

[4] Wu Zhangjun, Liu Xiao, Ni Zhiwei, et al. A market-oriented hierarchical scheduling strategy in cloud workflow systems[J]. The Journal of Supercomputing, 2013, 63(1): 256-293

[5] Yuan Dong, Yang Yun, Liu Xiao, et al. On-demand minimum cost benchmarking for intermediate dataset storage in scientific cloud workflow systems[J]. Journal of Parallel & Distributed Computing, 2011, 71(2): 316-332

[6] Wu Xiuguo. Migrating Workflow and Cloud Workflow[M]. Shanghai: Shanghai Jiaotong University Press, 2014 (in Chinese)

(吴修国. 迁移工作流与云工作流[M]. 上海: 上海交通大学出版社, 2014)

[7] Yuan Dong, Yang Yun, Liu Xiao, et al. A highly practical approach toward achieving minimum data sets storage cost in the cloud[J]. IEEE Trans on Parallel & Distributed Systems, 2013, 24(6): 1234-1244

[8] Li Xiu, Song Jingdong, Huang Biqing. A scientific workflow management system architecture and its scheduling based on cloud service platform for manufacturing big data analytics[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(1): 119-131

[9] Wu Zhangjun, Ni Zhiwei, Gu Lichuan, et al. A revised discrete particle swarm optimization for cloud workflow scheduling[C] //Proc of IEEE CIS 2010. Piscataway, NJ: IEEE, 2010: 184-188

[10] Yang Yuli, Peng Xinguang. Trust-based scheduling strategy for cloud workflow applications[C] //Proc of IEEE 3PGCIC 2013. Piscataway, NJ: IEEE, 2013: 316-320

[11] Wang Mingjun, Zhang Jinghui, Dong Fang, et al. Data placement and task scheduling optimization for data intensive scientific workflow in multiple data centers environment[C] //Proc of the 2nd Int Conf on Advanced Cloud and Big Data. Piscataway, NJ: IEEE, 2014: 77-84

[12] Liu Shaowei, Kong Lingmei, Ren Kaijun, et al. A two-step data placement and task scheduling strategy for optimizing scientific workflow performance on cloud computing platform[J]. Chinese Journal of Computers, 2011, 34(11): 2121-21305 (in Chinese)

(刘少伟, 孔令梅, 任开军, 等. 云环境下优化科学工作流执行性能的两阶段数据放置与任务调度策略[J]. 计算机学报, 2011, 34(11): 2121-2130)

[13] Simmhan Y, Barga R, Ingen C V, et al. Building the trident scientific workflow workbench for data management in the cloud[C] //Proc of IEEE ADVCOMP’09. Piscataway, NJ: IEEE, 2009: 41-50

[14] Lin Bing, Guo Wenzhong, Chen Guolong, et al. Cost-driven scheduling strategy for scientific workflow under multi-cloud environment[J], Pattern Recognition and Artificial Intelligence, 2015, 28(10): 865-875 (in Chinese)

(林兵, 郭文忠, 陈国龙, 等. 多云环境下基于代价驱动的科学工作流调度策略[J]. 模式识别与人工智能, 2015,28(10): 865-875)

[15] Li Xuejun, Xu Jia, Zhu Erzhou, et al. A novel computation method for adaptive inertia weight of task scheduling algorithm[J]. Journal of Computer Research and Development, 2016, 53(9): 1990-1999 (in Chinese)

(李学俊, 徐佳, 朱二周, 等. 任务调度算法中新的自适应惯性权重计算方法[J]. 计算机研究与发展, 2016, 53(9): 1990-1999)

[16] Sun Xin, Li Qingzhou, Zhao Pu, et al. An optimized replica distribution method for peer-to-peer network[J]. Chinese Journal of Computers, 2014, 37(6): 1424-1434 (in Chinese)

(孙新, 李庆洲, 赵璞, 等. 对等网络中一种优化的副本分布方法[J]. 计算机学报, 2014, 37(6): 1424-1434)

[17] Li Jianzhong, Liu Xianmin, An important aspect of big data: Data usability[J]. Journal of Computer Research and Development, 2013, 50(6): 1147-1162 (in Chinese)

(李建中, 刘显敏. 大数据的一个重要方面: 数据可用性[J]. 计算机研究与发展, 2013, 50(6): 1147-1162)

[18] Cao Jie, Zeng Guosun, Niu Jun, et al. Availability-aware scheduling method for parallel task in cloud environment[J], Journal of Computer Research and Development, 2013, 50(7): 1563-1572 (in Chinese)

(曹洁, 曾国荪, 钮俊, 等. 云环境下可用性感知的并行任务调度方法[J]. 计算机研究与发展, 2013, 50(7): 1563-1572)

[19] Ocana K A C S, De Oliveira D, Dias J, et al. Optimizing phylogenetic analysis using SciHmm cloud-based scientific workflow[C] //Proc of the 7th IEEE Int Conf on eScience. Piscataway, NJ: IEEE, 2011: 62-69

[20] Zhou Jing, Wang Yijie, Ruan Wei, et al. Research on massive data oriented data consistency[J]. Computer Science, 2006, 33(4): 137-140 (in Chinese)

(周婧, 王意洁, 阮炜, 等. 面向海量数据的数据一致性研究[J]. 计算机科学, 2006, 33(4): 137-140)

[21] Li Mohan, Li Jianzhong, Gao Hong, Evaluation of data currency[J]. Chinese Journal of Computers, 2012, 35(11): 2348-2360 (in Chinese)

(李默涵, 李建中, 高宏. 数据时效性判定问题的求解算法[J]. 计算机学报, 2012, 35(11): 2348-2360)

[22] Zhu Xiaomin, Wang Ji, Guo Hui, et al. Fault-tolerant scheduling for real-time scientific workflows with elastic resource provisioning in virtualized clouds[J]. IEEE Trans on Parallel & Distributed Systems, 2016, 27(12): 3501-3517

[23] Giorgini P, Mylopoulos J, Nicchiarelli E, et al. Reasoning with goal models[C] //Proc of Int Conf on Conceptual Modeling. Berlin: Springer, 2002: 167-181

[24] Calheiros R N, Ranjan R, Beloglazov A, et al. CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms[J]. Software Practice & Experience, 2011, 41(1): 23-50