风致弱振下高层建筑舒适性评价研究
2020-05-10李文煌
李文煌
(武汉理工大学土木工程与建筑学院 武汉 430070)
0 引言
随着轻质高强材料的发展,高层建筑变得轻且柔。风荷载作用下结构的振动响应较为显著,结构中的人常会感觉不舒适,振动舒适度问题十分突出。
弱振与强振不同,主要研究振动舒适度问题。何卫、谢伟平等[1-4]基于国内多座特大型高铁枢纽站、人行桥、大跨体育场馆、宽幅钢箱梁桥的实测资料,提出了基于舒适度评价的结构精细化模型的构建方法。并对强振与弱振的区别进行了界定,分析了二者在模型简化方法上的差异,阐述了舒适度研究时模型精细化的必要性。这些研究成果对高层建筑精细化模型的建立有很好的借鉴作用。
国内外很多学者都对高层建筑进行了现场实测研究,都得出一个相同的结论,即根据现场实测数据识别得到的模态频率值都大于计算模型修正前的模态频率值。CAMPBELL S等[5]对中国香港两栋高层住宅楼进行了现场实测,并且通过模态分析结果,他发现,现场实测数据识别得到的各方向的模态频率值都高于有限元模型模态分析得到的频率值;国内学者LI Q S等[6]现场实测了广东国际大厦,通过分析得到实测数据识别的两个平动方向的前三阶频率均高于有限元模型模态分析得到的自振频率;还有徐安等[7]对广州中信广场进行了现场实测,李秋胜等[8]对台湾台北101大楼进行了现场实测,林巍等[9]对中国香港K11大楼进行了台风下的实测研究,以上学者通过实测研究,都发现了相同的问题。
针对此问题,LI B等[10]对非结构构件进行了研究,探讨其对抗侧刚度的影响,他发现在这些非结构构件中填充墙对抗侧刚度的影响最大,达到了60%;SOYOZ S等[11]对一栋建筑物的隔墙拆除前后进行动力测试,发现模态频率变化幅度非常大,并且表明如果在有限元分析中不考虑隔墙,这种建模误差会很大;ASTERIS P G等[12]提出填充墙增加了结构的刚度和质量,导致结构基本周期显著的变化。这些研究中大多以地震等强振为前提条件,考虑填充墙对结构刚度的贡献,但这种前提假设并不具备合理性,因为地震时,填充墙会破坏。以上国内外研究虽然得到了一些有价值的结论,但也存在一些问题,如对计算模型的研究大多基于强振的前提、不合理地提高材料的弹性模量等。
我国规范当中也有将填充墙作为一种重要的非结构构件并且建议将其加入到结构的计算模型中。例如《高层建筑混凝土技术规程》(GB 50011—2010)[13]中建议地震时不能忽视填充墙对结构抗侧刚度的影响,在进行数值模拟时应该对结构的自振周期进行削弱,有这种观点的主要原因是为实际中更大的地震考虑。但是对于除了地震作用以外的其他激励,没有相关规定,还是利用基于结构安全的模型进行动力分析。
本文基于高层建筑风振舒适度评价的目的,建立了某沿海高层建筑的初始有限元模型。考虑填充墙、楼板装饰面层、楼梯、活荷载取值四种精细化模型修正因素分别建立有限元模型,分析每种修正因素对结构动力特性的影响程度。最后综合以上四种因素建立该结构的精细化模型,并与实测值进行对比,验证了精细化计算模型的正确性。基于线性滤波法模拟风荷载,对结构进行动力分析,综合国内外舒适度评价标准,评价了该建筑的风振舒适度。
1 工程概况及结构动力测试
某沿海高层建筑,其主体结构总层数为46层,总高度为168 m,结构形式为框架-核心筒。结构标准层平面图及传感器测点布置如图1所示。
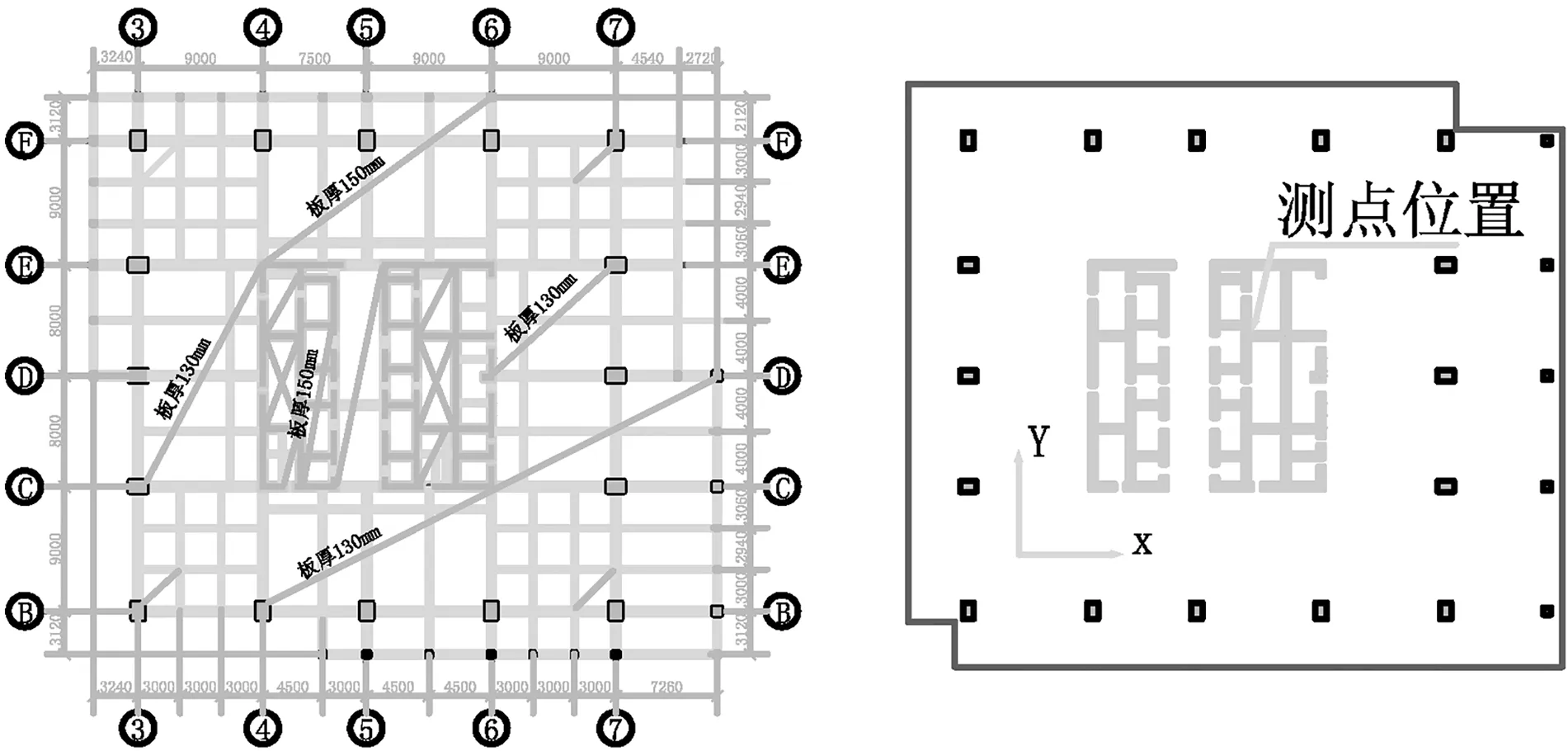
(a)标准层平面 (b)测点布置
图1 结构标准层平面图及测点布置
为了获得更全面的模态信息,测点数自然越多越好,但是实践中传感器数量有限,且结构体型较大,仪器较难布设,因此本文在竖向测点选取时采用了移动测点法进行测试。选取的实测测点层为10,13,18,25,28,32,35,42层,分别测试X,Y方向的振动信息。
采用环境激励下的测试数据进行模态参数识别。根据峰值拾取法,利用MATLAB进行编程并识别得到结构X和Y向前三阶模态频率,见图2。

(a)25层楼板X向自功率谱

(b)25层楼板Y向自功率谱
模态频率的识别结果如表1所示。

表1 实测数据模态识别结果
2 初始模型模态分析结果及评价
采用ANSYS建模,其中梁、柱采用Beam188单元进行模拟,楼板和墙体采用Shell63单元进行模拟,模型底部采用固接约束的边界条件。建立该高层建筑的初始有限元模型,即不考虑非结构构件影响的结构承载力模型,如图3所示。对初始有限元模型进行模态分析,将计算频率与实测频率进行对比,结果如表2所示。
从表2可以看出,初始模型计算频率与实测频率值相差很大,除了X、Y向第三阶频率和Y向二阶频率相对误差低于20%以外,其他各阶频率相对误差都在20%以上,最大相对误差出现在X向一阶,高达33.25%。
3 精细化模型建立的方法
3.1 精细化模型需考虑的修正因素
(1)填充墙。填充墙作为一种非结构构件,一般只起到分隔的作用,因此当结构受到剧烈振动时,填充墙会迅速破坏,与主体结构分离,最终失去效力,对结构刚度的贡献非常小,因此强振分析时通常不会考虑填充墙的影响,从而使结构更安全。而当结构处于弱振环境下时,比如风荷载的作用下,结构各部件都处于线弹性、小变形的状态,此时填充墙不会发生破坏,其与主体结构一起振动,对结构的侧向刚度提供贡献,因此弱振时不能忽略其影响。

图3 初始有限元模型
表2 计算频率与实测频率对比

阶次实测频率/Hz初始模型频率/Hz相对误差/%X向一阶0.400.26733.25Y向一阶0.380.27527.63X向二阶1.250.95723.44Y向二阶1.371.17214.45X向三阶2.472.11214.49Y向三阶2.902.51913.14
(2)楼板装饰面层。同样,楼板装饰面层也属于非结构构件,其与混凝土楼板在弱振情况下不会产生分离,因此同样参与结构的微幅振动,影响结构的质量分布以及刚度特性,因此也必须考虑其对结构动力特性的影响。实际工程中,楼板装饰面层的厚度有时甚至超过混凝土板的厚度,并且楼板装饰面层所用常见的材料类型中,有一部分材料的弹性模量大于混凝土,而另一部分则小于混凝土的弹性模量,如果在弱振情况下不考虑楼板装饰面层产生的刚度和质量效应,必定对结构动力特性产生一定的影响。何卫等[1]在进行大跨度车站结构楼板振动舒适度评价时,对其影响进行了分析,发现其对楼板动力特性的影响不容忽视。
由于楼板装饰面层所用材料弹性模量取值大小不一,为了建模的方便,本例中采用刚度和质量等效的原则,通过增加混凝土楼板的厚度等效考虑装饰面层的刚度,通过调整材料密度等效考虑装饰面层的质量。楼板装饰面层示意图如图4所示,楼板增加的厚度即装饰面层的厚度,约为50 mm。
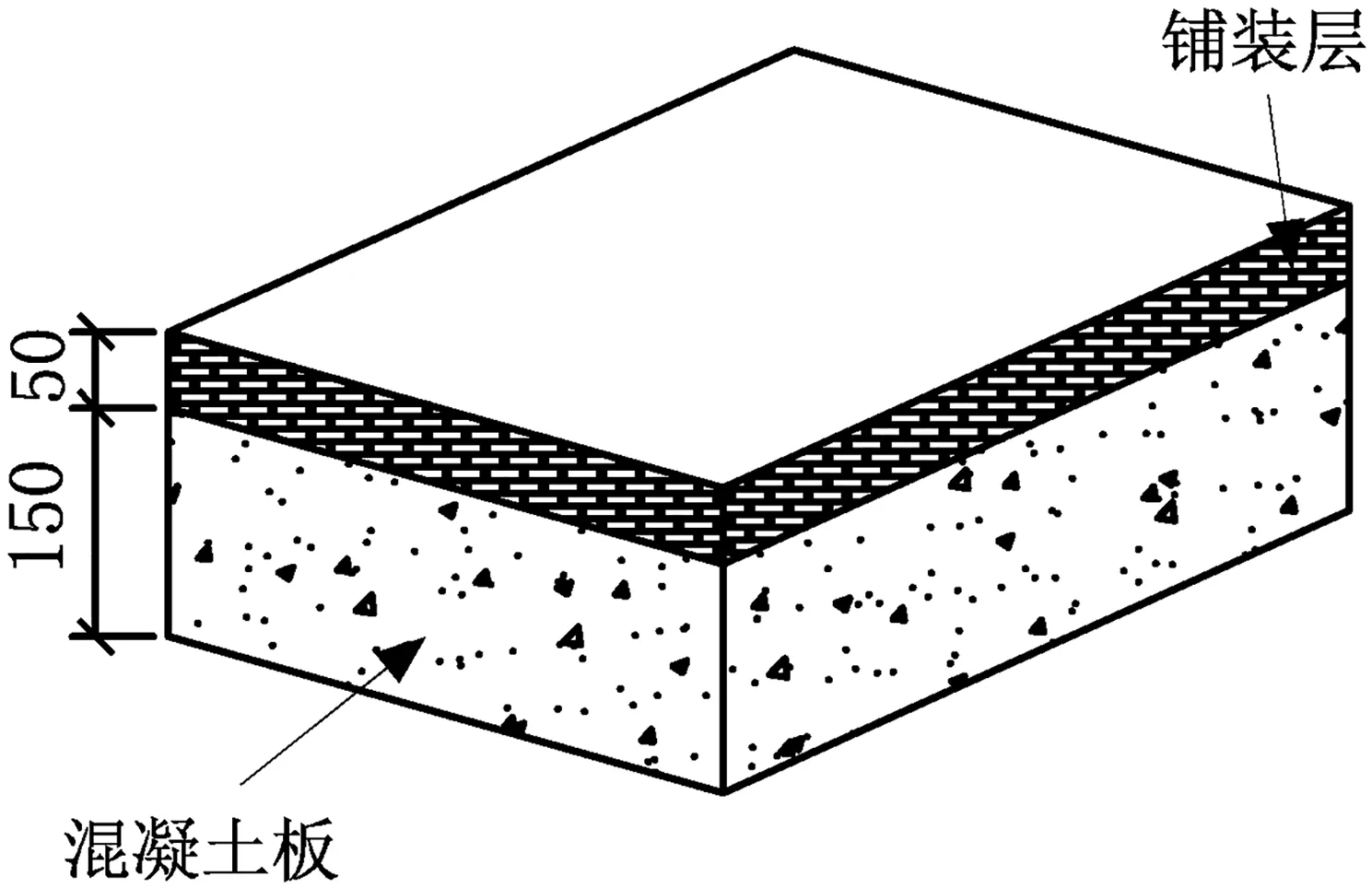
图4 楼板装饰面层示意(单位:mm)
(3)楼梯。强振计算时可视为自由边界或较弱连接的温度缝、楼(电)梯井、门窗洞口、螺栓连接节点等,在弱振下应适当考虑其约束或使原有约束增强。由于楼梯是现浇钢筋混凝土制成,其对整栋建筑的刚度影响较大,因此将其建立在有限元模型中是有必要的。本文利用壳单元来模拟楼梯,既考虑了其刚度效应,又考虑了其质量效应。
(4)活荷载取值。弱振下,结构中的活荷载随着结构的振动而同步振动,因此其会影响结构的质量分布,虽然有多少活荷载参与结构的振动并不能完全确定,但是参与振动的活荷载使结构的动力特性发生改变。我国抗震规范中规定一般民用建筑的活荷载组合值系数取0.5,但是结构抗震设计考虑的是强振,目的是使结构更加安全,因此活荷载组合值系数取值偏大,但是在弱振下,活荷载取值应适当减小,这样才更合理。但同时地震较风荷载而言,其发生的概率较小,而且由于振动幅度较大,活荷载与之同步振动的可能性较低,而风荷载作用下,结构振动幅度较小,活荷载与之同步振动,因此在弱振下,此时活荷载取值应该增大。本例中按建筑抗震设计规范中的规定取值,以0.5倍的活荷载设计值参与结构的振动。
活荷载的质量在ANSYS里可以通过单元附加质量的形式进行模拟,但以这种形式进行模拟时,体系自由度增多,因此求解速度较慢,效率较低。本文采用质量等效的原则,通过改变混凝土楼板的密度参数来实现。
3.2 精细化模型的建立及模态相关性分析
为了方便探究精细化建模过程中各个修正因素影响的大小,分别建立以下几种模型。
模型1:初始计算模型;
模型2:在初始计算模型的基础上单独考虑填充墙的修正;
模型3:在初始计算模型的基础上单独考虑楼板装饰面层的修正;
模型4:在初始计算模型的基础上单独考虑楼梯的修正;
模型5:在初始计算模型的基础上单独考虑0.5倍活荷载取值的修正;
模型6:在初始计算模型的基础上综合考虑4种因素的修正,建立精细化计算模型。
各模型计算频率与实测频率的比较结果如表3所示。
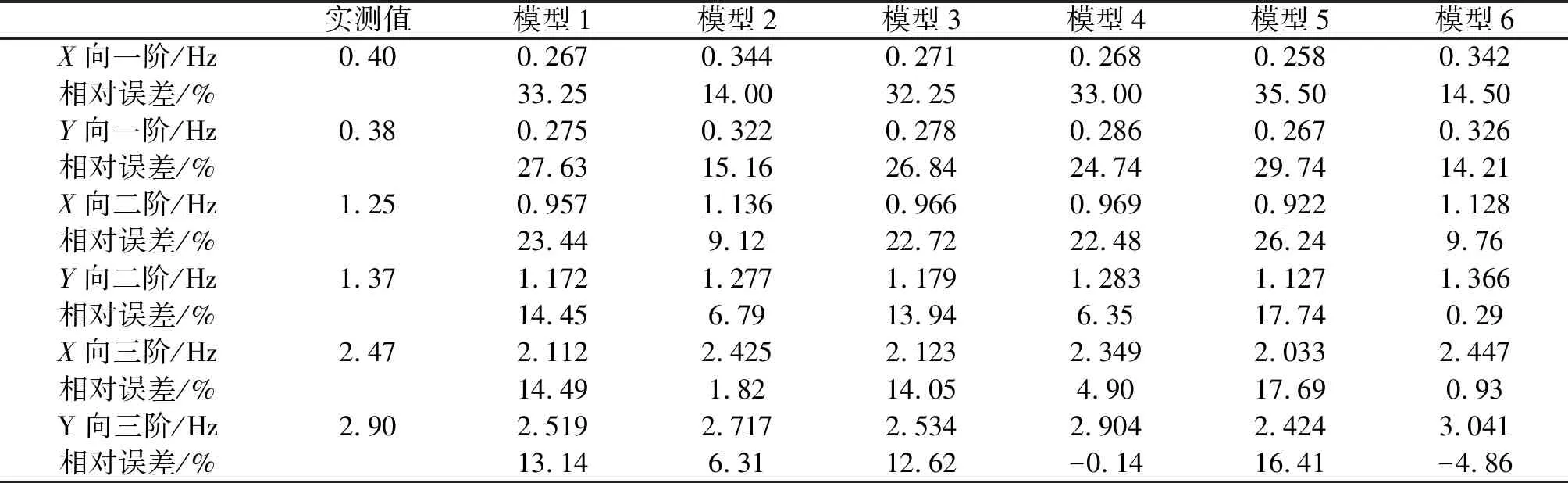
表3 计算频率与实测频率对比及相对误差
通过以上数据的对比,可以发现:
(1)填充墙、楼板装饰面层和楼梯三种修正因素均提高了结构各方向的自振频率,填充墙的影响最大,在初始模型X向一阶频率的基础上提高了19.25%;其次是楼梯,可以看出初始模型加入楼梯后,Y向频率提高的幅度明显大于X向,主要是因为Y向与楼梯的走向相同,刚度较X向大;影响最小的是装饰面层,约1%;由于加入0.5倍的活荷载,模型的质量效应大于刚度效应,因此出现计算频率下降的现象,但下降的幅度很小,约2%。
(2)精细化计算模型的自振频率与实测的自振频率较为接近,X、Y向一阶频率相对误差在14.5%以内,并且二阶、三阶频率相对误差都低于10%,说明修正后的模型能满足工程上对精度的要求,证明了本文所研究的4种因素的确对结构的动力特性有着不同的影响;但是精细化计算模型与实测数据之间还是存在一些差距,可能的原因是现场实测数据并不是很准确,或是结构外表的幕墙以及其他少量非结构构件并未考虑在内的缘故。
4 风振舒适度评价
4.1 风荷载模拟及动力响应计算
线性滤波法中的自回归(AR)模型具有计算量小,计算速度快的优点,从而被广泛的应用在风速时程模拟中。陈俊儒等[14]采用AR模型方法模拟了高层建筑的脉动风速时程,验证了基于AR模型模拟高层建筑脉动风速时程的可行性。
本文采用Davenport谱,对该建筑各层楼板处顺风向脉动风速时程进行模拟,并且将模拟风速谱和目标谱进行对比,验证了模拟的有效性。图5所示为28层一点处的脉动风速时程,模拟功率谱与目标功率谱的对比如图6所示。
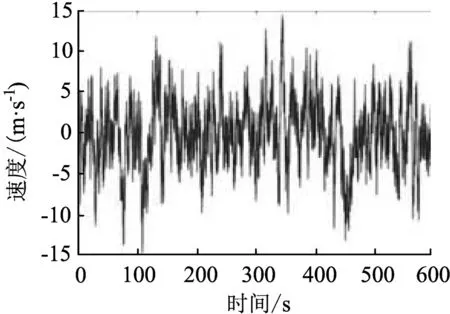
图5 28层一点处脉动风速时程

图6 模拟谱与目标谱比较
通过风速风压关系,将脉动风速时程转换为脉动风荷载时程,通过ANSYS软件分别加载到初始有限元模型和精细化有限元模型上,阻尼比取0.02,计算得到两个模型X和Y向的顶层风振加速度响应结果,如图7和图8所示。
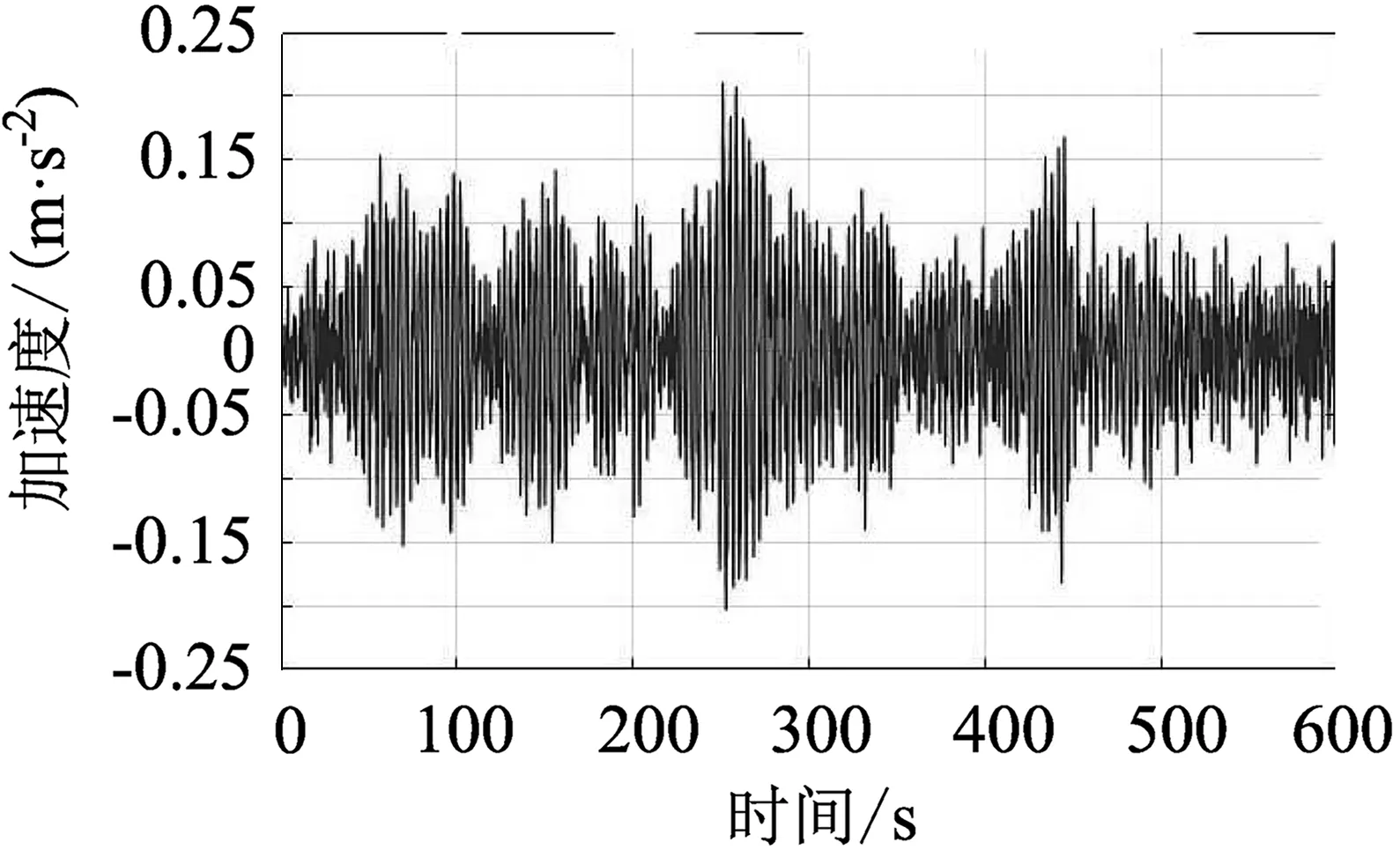
(a)初始模型X向加速度响应
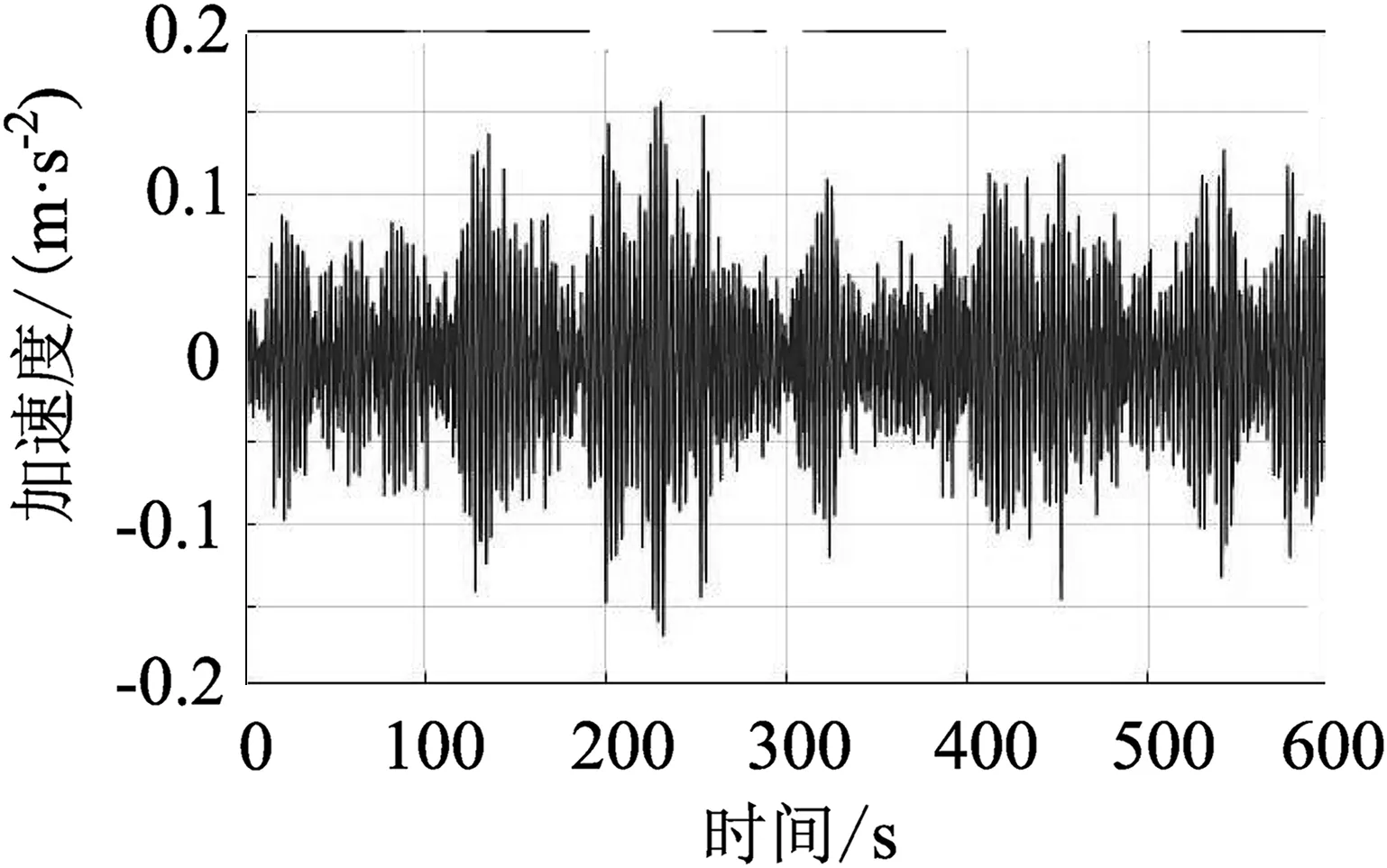
(b)精细化模型X向加速度响应
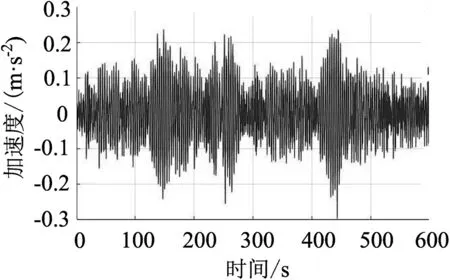
(a)初始模型Y向加速度响应

(b)精细化模型Y向加速度响应
从图7和图8中可以看出,精细化模型加速度响应峰值较初始模型有所降低,这和国内外学者的研究结论是相符的。
4.2 风振舒适度评价
本文采用以下4种舒适度标准进行评价:
(1)ISO 6897-1984[15]标准是以结构在10 min内的加速度均方根值为标准来进行评价,风荷载重现期取为5 a,限值与结构响应频率有关。
(2)ISO 10137-2007[16]标准的风荷载重现期取为1 a,并以所评价结构一阶振动频率对应的峰值加速度为评价指标,限值与频率大小有关,办公建筑和公寓建筑不同。
(3)加拿大NBC-2005[17]规范以结构在60 min内的峰值加速度为指标进行舒适度评价的,风荷载重现期取为10 a。加速度限值为住宅,15 cm/s2;办公,25 cm/s2,限值与频率无关。
(4)中国规范《高层建筑混凝土技术规程》[13]采用的也是10 a重现期风荷载下与频率无关的峰值加速度指标。横风向和顺风向结构顶点最大加速度限值为住宅和公寓,0.15 m/s2;办公旅馆,0.25 m/s2。
由于各标准对应的风荷载重现期不同,因此取同一指标进行对比时,需要对各标准做相应的转换,本文取风荷载重现期为10 a。ISO规定5 a标准转化成1 a时乘0.72,1 a到10 a可简单按照1.66的比例转换[18]。初始模型和精细化模型的计算结果及评价结果见表4及表5。
从表4和5看出,在X向顺风向上,无论加速度均方根值还是峰值,精细化模型的舒适度评价结果都满足要求,而初始模型舒适度评价结果不满足ISO 6897标准。在Y向顺风向上,精细化模型的舒适度评价结果除了不满足ISO 6897标准的均方根限值以外,其他标准都满足,而初始模型舒适度评价结果对所有标准都不满足。并且还可以看出精细化模型的两种加速度指标均小于初始计算模型,计算值的最大相对误差为28.37%。这种理论与实际的误差进一步验证了精细化模型的必要性,因此采用能反映结构真实动力特性的精细化模型能更合理地评价建筑的风振舒适度。

表4 X向风振舒适度评价结果

表5 Y向风振舒适度评价结果
5 结论
本文分析了高层建筑基于风振舒适度评价的计算模型与基于结构安全的计算模型的不同之处,提出了基于风振舒适度评价的精细化计算模型。论述了精细化模型应该考虑的四个因素。通过一个实际工程为例,研究得出以下结论:
(1)在弱振条件下,填充墙、楼板装饰面层、楼梯和活荷载取值对高层建筑的动力特性具有一定的影响,填充墙对结构刚度的影响最大。通过对比发现,在计算模型中考虑填充墙、楼板装饰面层、楼梯三种因素使结构的自振频率提高。
(2)相比基于安全的计算模型,精细化计算模型的动力特性与实测值吻合较好,更能反映结构的实际振动状况。此结论可以适用于存在本文论述的精细化因素的高层建筑中。
(3)对于实际工程中实测加速度值往往小于理论计算值的现象,精细化模型提供了一种很好的解释,评价高层建筑的风振舒适度时,应采用精细化模型进行计算。
