基于三维约束NewWave理论的自升式钻井平台动力响应分析

王维刚，陶 京，周国强，宁印斌，赵开龙

(1. 东北石油大学 机械科学与工程学院，黑龙江 大庆 163318; 2. 中海石油(中国)有限公司深圳分公司，广东 深圳 518000; 3. 中国石油集团工程技术研究院有限公司，天津 300451)

自升式钻井平台是在相对较浅水下作业的可移动钻井平台。当60多年前首次引进这种装置时，仅适用于水深70 m以下作业。由于它们具有移动性和固定性的优点，加上在较深水域开采石油和天然气的便利性，对这些装置的需求与日俱增。由于处于较深水域作业和日益严峻的环境限制，平台的安全构成较大的威胁，尤其当平台的固有振动频率接近波动频率时，会引起平台的共振。因此有必要对自升式钻井平台的动力响应进行研究[1-2]。

在自升式平台的动力响应分析中，应考虑与平台结构性能相关的所有不确定性，其中一个主要的不确定因素是由波浪的随机性导致的[3]。由于海浪具有不规则、非线性和方向性的特点，波浪建模的合理性直接影响评价结果的准确性。波浪建模方法包括设计波法、随机分析等方法[4]。在设计波方法中选择适当的规则波来描述波特征。该方法的缺点是波能仅由一个波频率表示，忽略了海浪的宽谱特征和随机性。随机分析方法利用由许多简单波叠加的不规则波来描述波特征，其中简单波相位呈随机性分布。基于此方法得到的结构最大应力、位移等响应在某一置信度内认为是非常可靠的。该方法的不足是模拟时间较长、计算成本较大，并且在可能出现极值的时间序列中仅模拟少量有效波。

针对此问题，Tromans等[5]在1991年提出了NewWave理论，该理论是基于统计学原理严格推导出来的，表述为极端波面可由不同频率成份的波浪零相位线性叠加而成，虽然是确定性的，但在一定程度上可以反映波浪的随机性。Taylor等[6]提出了约束NewWave理论，它在综合考虑波浪的谱性、随机性和非线性的基础上，对随机过程中的波高值进行预先设定，能够很好地体现大波效应，且计算效率得到了极大的改善。然而，约束NewWave仅作为二维水波面高程作用在结构之上，本质上是二维波，且没有考虑波浪传播效应。Cassidy等[7]利用定向NewWave波解决了波浪传播效应，但没有明确考虑波浪的随机特性。Mirazdeh等[8]对二维约束NewWave波进行了延伸，生成了三维约束NewWave波，该方法综合考虑了海洋波浪传播和随机背景的影响，且计算耗时较短。

基于三维约束NewWave理论，建立某122 m自升式钻井平台的有限元分析模型，针对风暴自存工况，对该平台进行模态及动力学分析，研究波浪方向性和随机性对平台动力响应的影响。

1 三维约束NewWave理论

二维约束NewWave理论通过在随机时间序列中约束NewWave波来生成。通过对二维约束NewWave进行扩展，可生成三维约束NewWave。不同波长、幅值和周期的波浪以不同速度和方向传播，这些波叠加可产生随机波浪高程。对于有向波浪，在某个点(如(X,Y)=(0,0))的瞬时随机波面高程定义如下：

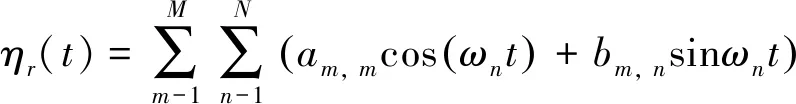
(1)

式中：am, m和bm, m为傅里叶分量，它们均是独立高斯随机变量，其均值为零，方差的表达式如下：

(2)

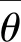
(3)

工程上通常用的定向传播函数可表示为：

(4)

式中：S是正整数，文中取4；CS是满足方程(4)的系数。

三维约束NewWave理论波面高程时间历程函数为：

(5)

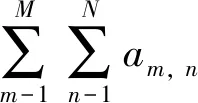
预先设定风暴自存工况下的最大波峰高度为17.46 m，跨零周期为17.22 s，波浪谱选用P-M谱。图1为分别利用随机波、NewWave波和约束NewWave波生成的波面高程。可以看出，在随机背景下，由约束NewWave生成的波面不但反映了波浪的随机特性，而且波面的幅值谱也能很好地体现大波效应。

图1 不同波浪理论的波面高程随时间历程对比Fig. 1 Comparison of wave surface elevation with time history in different wave theories

2 自升式钻井平台建模

2.1 结构建模

某122 m自升式钻井平台结构如图2所示，主要由平台结构、钻井装置、桩腿、桩基和升降装置等组成。其中桩腿为空间桁架式结构，侧视图和横截面如图2(b)、2(c)所示。平台主体结构为高强钢，屈服应力为355 MPa；桩腿弦杆的屈服应力为690 MPa，水平横撑的屈服应力为520 MPa，斜撑的屈服应力为240 MPa。自升式钻井平台的主要尺寸为：长度70.358 m，宽度76 m，型深9.45 m，桩腿总长166.98 m。

图2 自升式钻井平台结构简图Fig. 2 Schematic diagram of jack-up drilling

2.2 桩基建模

图3 自升式钻井平台有限元等效模型Fig. 3 Finite element equivalent model of jack-up platform

对于自升式钻井平台这种复杂结构，合理地简化结构和建立模型是非常重要的。文中对起主要支撑的桩腿结构进行了详细模拟，对船体进行了简化处理，关于桩腿弦杆的简化可参考SNAME[9]，基于ANSYS建立的有限元模型，如图3所示。在该模型中，采用梁单元BEAM188对平台主船体结构进行仿真；采用管单元PIPE288对泥线以上的桩腿进行仿真；对桩腿与船体以及桩腿与土壤的连接采用弹簧单元combin14；桩腿与船体间的y向扭转刚度系数Kry、z向扭转刚度系数Krz、垂向位移刚度系数Kv的计算可参考文献[10]。经计算可知Kry=Krz=9.25×1011N/m，Krz=9.14×1011N/m；对于桩腿的P-Δ效应，通过在桩腿与船体之间添加水平方向的负刚度弹簧来实现，负刚度Kpd的计算可参考文献[11]，经计算Kpd=1.130×106N/m。由于模型中忽略了平台钻井、起重等上部结构，因此采用质量单元mass21来弥补，并通过重心进行调整，使模型重心与实际重心重合。

为了克服等效线性弹簧模型的局限性，可在桩-土界面上分布非线性弹簧来考虑桩-土的相互作用，该结论在文献[12]中已得到验证。分布弹簧可用载荷-位移曲线来表征，美国石油学会(API)[13]提供了三种载荷-位移曲线，这些曲线随侧向位移(y)和深度(z)呈非线性变化，包括侧向抗力对应的p-y曲线、竖向抗力对应的t-z曲线和桩尖承载抗力对应的Q-z曲线，其中，p、t和Q是弹簧力，且弹簧力随土壤性质和结构的y或z位移大小而变化。这些曲线可以通过现场测试或API提供的经验公式获得。

表1给出了自升式钻井平台桩土主要特性参数。据此通过API经验公式可获得p-y、t-z和Q-z三条曲线，然后可转化为非线性弹簧单元Combin39的载荷-位移数据，从而可达到模拟桩-土相互作用的目的。

表1 桩土主要特性参数Tab. 1 Main characteristic parameters of pile and soil

3 动力响应分析

图3为某122 m自升式钻井平台的有限元分析模型。对该平台进行模态分析及风暴自存工况下的动力响应分析，风暴自存工况的主要参数如表2所示。本文只考虑波浪和海流在0°方向上的作用，波流载荷可按Morison公式计算。风荷载按CCS规范计算并作用于船的重心。

表2 风暴自存工况的计算参数Tab. 2 Calculation parameters of storm self-existence condition

3.1 模态分析

图4 基于非线性弹簧桩基的平台前三阶振型Fig. 4 First three order vibration pattern diagram of jack-up platform based on nonlinear spring pile

利用ANSYS程序的模态分析功能可确定结构的阻尼、频率及振型。分别采用非线性弹簧、线性弹簧、铰支及固支四种桩基模型对平台进行模态分析，基于非线性弹簧桩基模型的自升式钻井平台振型如图4所示，基于四种桩基模型的平台自振频率如表3所示。

由图4可知，自升式钻井平台的前三阶模态振型分别为横荡、纵荡和艏摇，这些结果为平台监测提供了理论支持。由表3可知，由固支桩基模型得到的平台固有频率最高，其次是线性弹簧、非线性弹簧，最低的是铰支桩基模型，说明由固支模型得到校核结果会存在安全隐患，铰支模型又过于保守，而线性弹簧和非线性弹簧模型可确保结果处于合理的范围。由于线性弹簧模型不能考虑土体的非线性刚度等非线性行为以及土体与地基之间可能产生的间隙等非线性行为，所以本文采用基于非线性弹簧桩基建模的方法，以进一步提升模拟准确度。

表3 自升式钻井平台不同桩基模型的自振频率Tab. 3 The natural vibration frequency of different pile foundation models of jack-up drilling platform

3.2 基于三维约束NewWave的动力响应分析

利用ANSYS程序的瞬态动力学分析功能可确定结构在静载荷及风、浪、流载荷作用下随时间变化的位移、弯矩等。对平台施加三维约束NewWave波进行动态和准静态分析，并分别基于甲板位移和基底剪力作为响应变量计算平台的动力放大系数(DAF)。图5和图6分别给出了甲板位移、倾覆弯矩的动响应和静响应。基于甲板位移求得的DAF为1.328，而用倾覆弯矩计算得到的DAF降至1.309 9。通过上述结果可知，基于甲板位移作为响应变量得到动力放大系数才能确保结构强度校核的有效性和合理性，因此后续分析均以甲板位移作为响应变量进行分析。

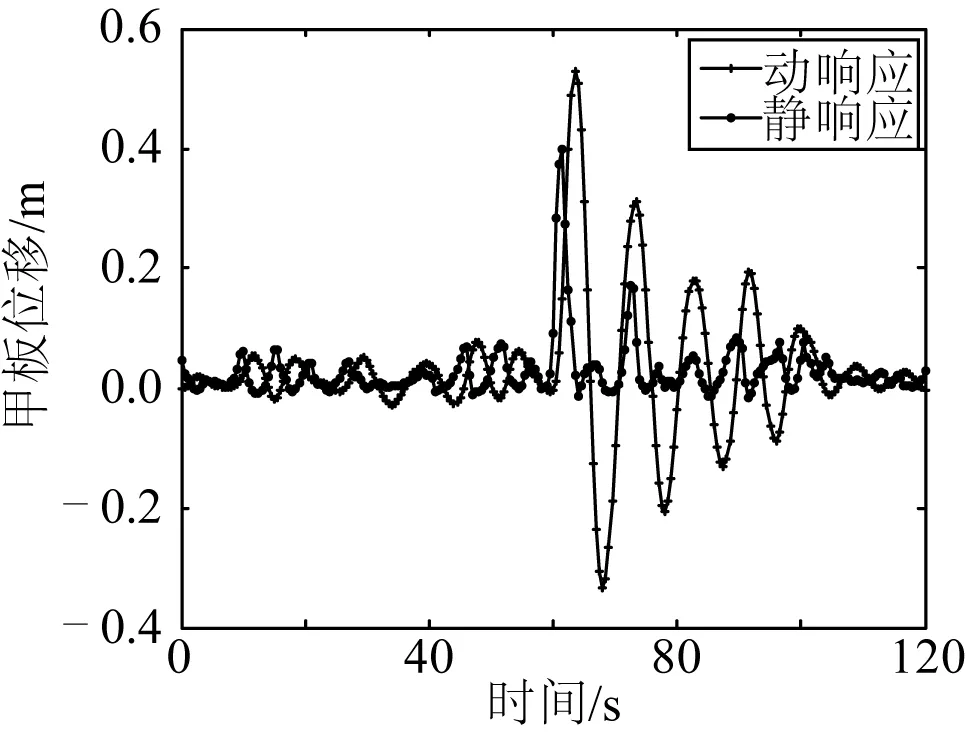
图5 甲板位移动静响应对比Fig. 5 Comparison of dynamic and static responses of deck displacement

图6 倾覆弯矩动静响应对比Fig. 6 Comparison of dynamic and static responses of overturning moment

图7给出了二维约束NewWave最大波峰集中在船体中心的甲板位移响应，该波的入射角为0°、最大波峰发生的时刻为60 s。由图可知，甲板最大位移为0.386 3 m，出现的时刻为61 s，即发生在最大波峰刚刚经过时。为了进行对比，基于相同二维约束NewWave波，对于最大波峰位置集中在迎风侧桩腿和背风侧桩腿两种情况进行了模拟，相应结果显示在图7中。结果表明，对所研究的自升式钻井平台和波浪条件，最大波峰集中在迎风侧桩腿处的响应最大，甲板最大位移为0.408 8 m，出现的时刻为62 s。因此在后续的分析中，将迎风侧桩腿处作为约束NewWave波峰出现的位置。

图7 约束NewWave最大波峰在不同位置时甲板最大位移对比Fig. 7 Comparison of maximum deck displacement when the maximum peak of constrained NewWave is at different positions

图8 二维和三维约束NewWave作用下甲板位移时程对比Fig. 8 Time history comparison of deck displacement under two-dimensional and three-dimensional constrained NewWave

为研究包含三维效应波浪传播对平台结构响应的影响，将二维和三维约束NewWave分别应用于自升式钻井平台结构中，其甲板位移的时程响应曲线如图8所示。从图8可知，基于三维约束NewWave得到最大甲板位移(0.283 8 m)小于基于二维约束NewWave得到的最大甲板位移(0.408 8 m)，表明当波浪波峰经过自升式钻井平台时，包含三维效应的波浪传播会降低甲板最大位移。

为了进一步评价三维约束NewWave的性能，提取了垂直于平均波浪方向的甲板位移时程数据，将其显示在图9中。对于二维约束NewWave，考虑对称结构和对称水波面，波浪力垂直分量的和为零，因此垂直波浪方向的甲板位移也为零。然而，对于三维约束NewWave，相对于沿水平波浪方向甲板位移而言，在垂直方向甲板以较小的幅值波动，其原因是平台垂直方向刚度远大于水平方向刚度。这表明在垂直方向的波浪力不为零，其原因是三维约束NewWave的水波面是不对称的。

为了评价三维约束NewWave中不同随机背景对结构响应统计的影响，用不同种子数分别产生100个二维约束NewWave波和100个三维约束NewWave波，最大波峰出现位置在迎风侧桩腿处，并将其作用于自升式钻井平台，进行动力响应分析。提取每个种子数对应的甲板位移，并用Weibull分布函数来表示，最大甲板位移的频率分布及Weibull拟合曲线如图10所示。从图10可以看出，由两种波所计算的甲板位移均符合Weibull分布；相对于三维约束NewWave，基于二维约束NewWave波拟合的Weibull曲线向右平移；甲板位移在三维波浪中的比二维小，其原因是三维波浪包含波浪传播。图11给出了不同波浪入射角度下，基于二维和三维约束NewWave两种理论最大甲板位移Weibull分布的平均值，从中也能证明包含波浪传播会极大地改变响应统计。

图9 基于三维约束NewWave甲板位移时程(甲板位移垂直于平均波浪方向)Fig. 9 Time-history of deck displacement in 3D constrained NewWave (deck displacement perpendicular to average wave direction)

图10 100个二维和三维约束NewWave作用下最大甲板位移Weibull分布对比Fig. 10 Weibull distribution comparison of maximum deck displacement under 100 2D and 3D constrained NewWaves

3.3 波浪传播对动力放大系数的影响

为了评价波浪传播对动力放大系数的影响，将基于二维和三维NewWave的结果与100个基于二维和三维约束NewWave的平均结果进行比较，如图12所示。

图11 二维和三维约束NewWave作用下最大甲板位移平均值随入射角变化情况对比Fig. 11 Comparison of the maximum deck displacement with wave incidence angle under 100 2D and 3D constrained NewWaves

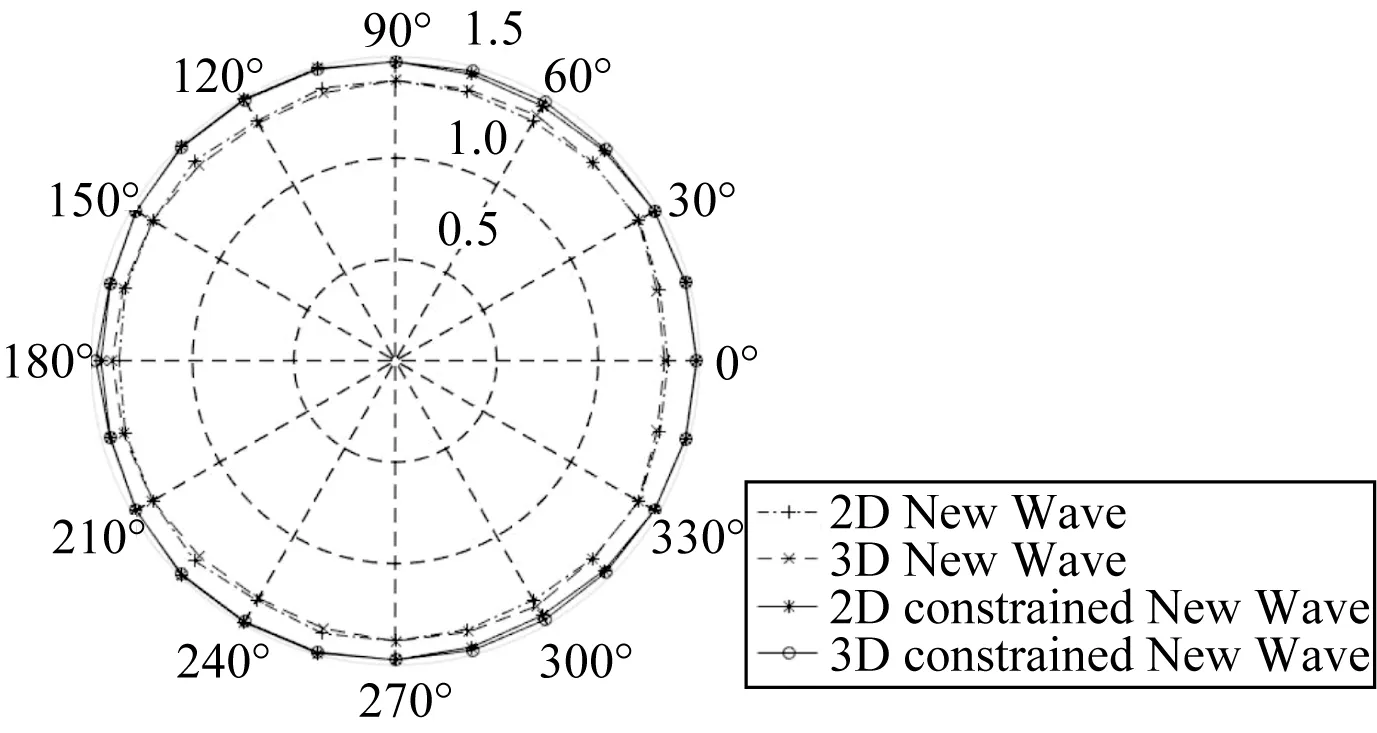
图12 基于四种不同方法动力放大系数对比Fig. 12 Comparison of dynamic amplification coefficients based on four different methods

从图12中可以看出，随着波浪入射角的增加，二维和三维波得到动力放大系数不同，但是这种变化没有明显的规律，即二维波不总是能产生较高的动力放大系数。但是相对于NewWave，包含随机背景的约束NewWave增加了动力放大系数。

4 结 语

以某122 m自升式钻井平台为研究对象，对其进行模态分析、动力响应分析，讨论波浪传播对动力放大系数的影响，研究结果表明：

1) 相比固支、铰支及线性弹簧模型，非线性弹簧桩基模型考虑了土壤和桩靴的相关参数，能够确保结果的合理性。

2) 通过对约束NewWave作用下平台响应分析可知，由倾覆弯矩确定的动力放大系数低于由甲板最大位移确定的动力放大系数，因此将甲板最大位移作为响应参数能确保平台结构性能安全。

3) 通过对比最大波峰在船体中心、迎风侧桩腿和背风侧桩腿时甲板的最大位移，可知峰值集中在迎风侧桩腿时平台的响应最大，因此应将迎风侧桩腿处作为约束NewWave波峰出现的位置，以确保结果的合理性。

4) 通过不同波浪模型下平台瞬态动力响应分析，结果发现，对波浪不同入射角度，相比二维波浪模型，包含波浪传播的三维波浪模型均会降低甲板最大位移，且动力放大系数也会降低。相比NewWave模型，考虑波浪随机性、谱性和非线性的约束NewWave波浪模型增加了动力放大系数。由此可知，三维约束NewWave波浪模型不仅能较准确地反映波浪的真实特性，而且能确保结构性能评估的安全性和合理性。