小数数学练习模式转变研究

叶少奉

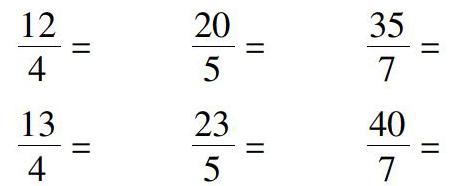
一直以来，练习是数学教学中必不可少的部分，是形成和巩固学生认知结构的过程，是培养学生数学能力的基本手段，也是发展学生智力的重要手段。因此，设计数学练习绝不是灵机一动、信手拈来的，而是一项充满创造性、启发性的行为。我尝试在练习方式上推陈出新，设计出具有趣味性、实践性和开放性的练习，同时，读懂编者意图，练好课本中的相关练习，很好地达到教学目标。让练习成为放飞学生潜能的天地。

一、思考探究，豁然开朗

概念教学是小学数学教学中至关重要的一个环节，是基础知识和基本技能教学的核心。学好概念是学好数学最重要的一环。一些学生之所以觉得学习数学很困难，概念不清往往是最直接的原因，这样就不能熟练地对数学概念进行理解、应用和转化等。因此，抓好概念教学对提高普通中学数学教学质量具有根本性的意义。但是，在现今的数学概念教学过程中，许多教师重解题、轻概念，忽视了学生对数学概念的理解，造成学生解题与概念脱节。

二、实践探究，有思有悟

例如，在学习“组合图形面积的计算”以后，我曾给学生布置这样的练习：有一块长9分数、宽4分米的红布，现在要把它剪成成边长2分米的正方形手帕。一共可以做多少块？ 学生的计算结果为（9×4）÷（2×2）=9（块），学生的操作结果为8块，为什么会出现不同结果？是计算有问题，还是操作不对？这些思考能帮助学生认清计算与实际操作之间的区别。《数学课程标准》在教学目的中将“能够运用所学的知识解决简单的实际问题”改为“能探索和解决简单的实际问题”，那么在练习中也应该有所体现。这一类练习可以更好地把数学知识与实际相联系，注重培养学生的应用意识和实践能力，鼓励学生自己去动手制作、实验、观察、思考。学生通过自己动手，训练了多种感官的协调作用，特别是把数学理论变为一种初步的成果，这对于小学生来说也是一种有意义的创新体验。

三、螺旋上升，领悟深刻

在课堂上，我引导学生对同一类问题进行螺旋上升練习，利于学生发现它们之间的联系和区别，认识到其本质特征。如在教学圆柱的体积这一内容后，我设计了这样的题组练习1.一个圆柱形石柱模型，底面积是28.26厘米2，高是10厘米，求这个圆柱模型的体积。 2.一个圆柱形石柱模型，底面半径是3厘米，高是10厘米，求这个圆柱模型的体积。3.一个圆柱形石柱模型，底面直径是6厘米，高是10厘米，求这个圆柱模型的体积。

在思考解答过程中，学生对圆柱的体积计算有了比较深刻的认识。这三道题的设计非常巧妙，第1题：求圆柱的体积直接用底面积乘高。第2题：先利用底面半径求出底面积，最后才用底面积乘高求出它的体积。第3题：先利用底面直径求出半径，接着求出底面面积，最后求圆柱的体积。把同一类问题的不同方面整合到一起，突出了三种形式的求圆柱的体积的题型。

四、对比探究，恍然大悟

这类练习的目的是为了使学生通过练习，在知识的内在本质和区别上形成对比，从而有所领悟。它可以是课堂教学的延伸和补充，把数学知识与学习方法渗透到教学活动中去。看上去是简单的组合，但影响却是深远长久的;它不同于平时的练习，必须有目的、有方向的。这样既能巩固了学生所学知识，又能让学生在综合性练习的过程中，通过对比探究，大彻大悟。 例如，在五级下册学生学习了真分数和假分数这一内容后，我设计了下面的一道题：

1.把下面的假分数化成整数或带分数。看你有何启发。

在学生独立完成后追问：观察它们的分子和分母，怎样的假分数能化成整数，怎样的假分数不能化成整数，只能化成带分数？从而让学生恍然大悟，当分子是分母的倍数时，这样的假分数就能转化成整数，反之，如果分子不是分母的倍数，这样的假分数只能转化成带分数。

总之，有效的练习设计不仅可以减轻学生负担，提高教学效率的有效举措，也是实施素质教育、培养学生创新精神和实践能力的重要途径。因此，我根据课堂教学的需要，围绕教学目标，遵循学生的认知规律设计有针对性的有效练习。我们教育所要培养的不是做练习的“机器”，而应是有思想有创新能力的人。教师只有正确地理解课堂练习的价值，更新教育观念，落实新课程理念，以学生的发展为本，加强练习的改革，实现“减负增效”，才能实现真正的“人本回归”。

责任编辑 徐国坚