基于最小一乘的虚拟阵元波束形成仿真研究

张伟民，郭海涛，金其余，田原嫄，焦圣喜

基于最小一乘的虚拟阵元波束形成仿真研究

张伟民1，郭海涛2，金其余3，田原嫄4，焦圣喜5

(1. 内蒙古大学电子信息工程学院，内蒙古呼和浩特 010021；2. 海南热带海洋学院海洋信息工程学院，海南三亚 572022；3. 内蒙古大学数学科学学院，内蒙古呼和浩特 010021；4. 东北电力大学机械工程学院，吉林吉林 132012；5. 东北电力大学自动化工程学院，吉林吉林 132012)

水下多波束成像系统成像质量的关键主要在于波束形成的质量。在信号频率一定时，常规相移波束形成只有通过增加基阵的孔径来得到更窄的波束，但是在有限的应用条件下，这种方法又受到实际工程的限制。因此，提出一种基于最小一乘估计的虚拟阵元波束形成方法。在低信噪比的情况下，利用最小一乘估计的稳健性可以得到更加准确的估计信号，从而在不增加基阵尺寸的情况下获得更窄和抗干扰性更强的波束，提高阵增益和声呐图像的角度分辨率。通过Matlab仿真并与其他方法比较验证，证明了上述方法的优越性。

多波束成像系统；最小一乘估计；稳健性；虚拟阵元；波束形成

0 引言

多波束成像声呐通常在辐射角度区域形成大量的窄波束，其特点是高分辨率[1]、高数据率、宽覆盖[2-4]且能够实时成像[5]。而这些波束的性能直接影响着成像声呐的方位分辨率[6-7]。常规波束形成只有通过提高信号的发射频率和接收阵列的孔径得到较窄的波束来提高图像的分辨率。由于实际情况中，高频信号衰减严重，阵列孔径不能做得很大。因此，在保证阵列增益、波束宽度等指标优良的条件下，减少阵元使用数成为阵列发展的趋势之一[8]，虚拟阵元波束形成就是在这种情况下产生的。此类算法能够使用较少的阵元数目得到较好的波束性能。人们在数理统计中用“稳健性”这个概念来描述异常值对某种方法的影响程度。虚拟阵元接收信号估计算法的准确性和稳健性决定了虚拟阵元波束形成的性能和应用的可靠性。

虚拟阵元波束形成是虚拟阵列波束形成方法中的一类，主要有线性预测法[9]、最小二乘法[9]和基于遗传算法的声矢量阵虚拟阵元波束形成法[10]等。线性预测法是将虚拟阵元的前个(或后个)阵元数据作为参考信号来实现虚拟阵元的构建。随着虚拟阵元数目的增加，估计结果会产生明显的累积误差。最小二乘法通过处理真实阵元接收信号来估计虚拟阵元接收信号。最小二乘法相比线性预测法估计结果更加准确且不产生累积误差。但实际海洋环境中的噪声较为复杂，接收信号中必然会存在异常值，而最小二乘法的稳健性较差，使估计误差增大。基于遗传算法的声矢量阵虚拟阵元波束形成是通过遗传算法优化得到估计系数，从而构建出虚拟阵元接收信号。但在回波信号信噪比较低时，实阵元接收到的信号复杂且奇异值较多，通过遗传算法优化得到的解容易陷入局部极值，使估计误差增大。

本文利用最小一乘(Least Absolute Deviation, LAD)在估计回归系数时稳健的优点[11-12]，给出一种基于最小一乘稳健估计的虚拟阵元波束形成方法。由于最小一乘计算困难，所以利用文献[13]线性规划方法快速准确地估计出最小一乘线性回归系数，从而解决了最小一乘求解难的问题。

1 最小一乘估计

1.1 线性预测模型

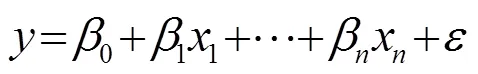
用向量及矩阵形式表示为

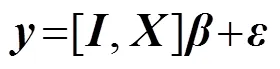
其中：为元素全为1的维列向量；

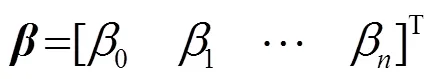
1.2 最小一乘线性回归系数估计算法

最小一乘的线性回归系数需要通过求解一个无约束不可微最优化问题来获得，即

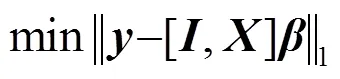
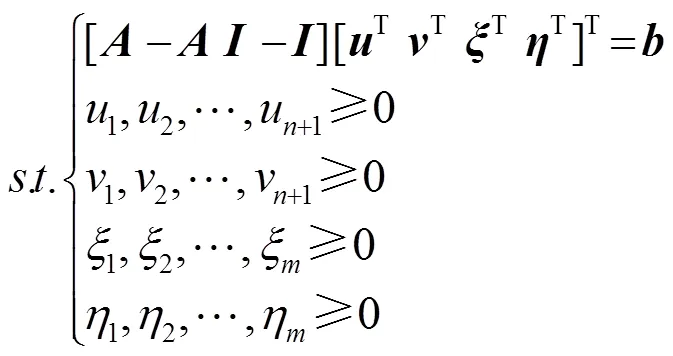
2 虚拟阵元波束形成的构建

2.1 信号模型与噪声模型

对于单频信号，基阵的指向性函数与阵元间隔有关，反映了信号在阵元之间存在一定的空间相关性[15]。这是虚拟阵元可以实现的理论依据。通过处理实阵元接收信号，估计构建出虚拟阵元接收信号，从而在理论上扩展了阵列的孔径。因为在应用最小一乘进行最优系数的估计时，需要在回波角度附近进行观测来获得多组观测方程，并根据这些方程求出最优解系数，所以当接收基阵形成单个波束时，构建虚拟阵元首先要对回波进行方位估计，这在很大程度上决定了信号估计的准确度。而多波束声呐具有很多的波束形成器，使各个波束顺序排列充满整个搜索空间，并进行空间分割，相当于许多部单波束声呐同时工作，每个波束形成器只负责指向一个角度，所以在进行虚拟阵元波束形成时无需进行方位估计。

现假设阵列为元均匀直线阵，处于目标回波声场的远场区，目标回波(,)可近似为平面波，回波信号频率为0，背景噪声为加性高斯限带噪声。不考虑各个阵元的指向性，将接收阵的第一个阵元作为基准阵元，回波与基阵垂直方向的夹角为0。如图1所示，斜线表示回波信号，图中黑色圆点为真实阵元，白色圆点为虚拟阵元。

在确定了信号频率与阵元数时，由线阵的指向性函数可知，波束受到入射角度的影响，所以忽略时间因素。回波信号可表示为

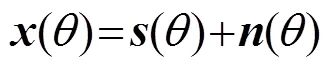
式中：s(θ)是无噪声的回波信号，即 ； ，为阵列相邻阵元接收信号之间的时延差；为加性高斯限带噪声。

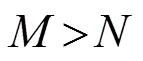
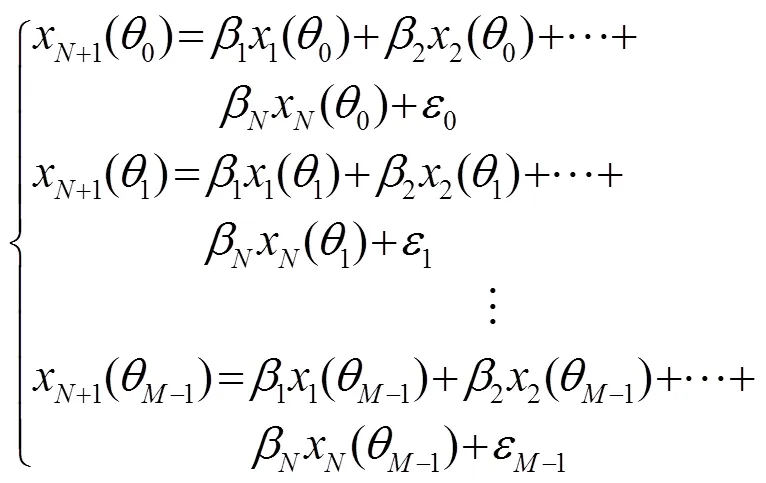
用矩阵形式可表示为

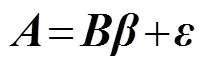
其中：

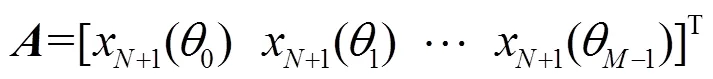
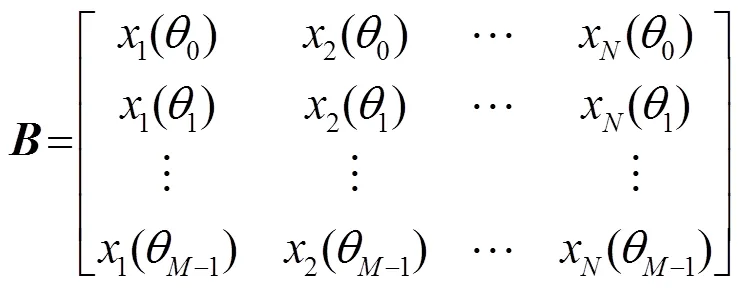
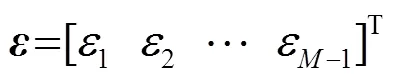
同理，可构建多个虚拟阵元的接收信号，即：

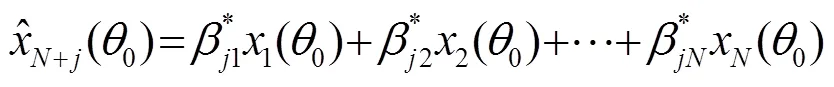
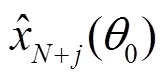
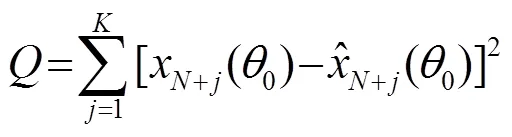
其中，值越小，说明估计的虚拟阵元信号越准确可靠。

2.2 阵增益

如图1所示，0表示回波信号入射方向与基阵法线的夹角，各阵元灵敏度一致，信号与噪声互不相关，且不同阵元接收的噪声也是不相关的。两个阵元信号之间的互相关系数为

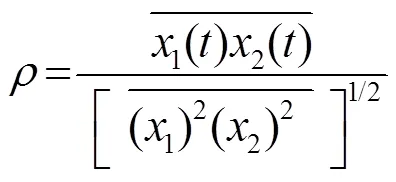
分子为两个阵元信号的时间平均，分母为归一化因子。利用虚拟阵元接收信号估计算法，使阵元数为的实阵列阵元数虚拟扩展至+个。由于信号环境复杂，观测数据不可避免地存在噪声，在构建虚拟阵元信号时必然会产生估计误差，误差大小可用值反映。各个实阵元信号中的噪声是非相关的，所以各虚拟阵元信号中的噪声是由各实阵元噪声的线性组合构成的，虚拟扩展后的阵列噪声包括实阵列中的非相关噪声和个虚拟阵元中的相关噪声。根据波束形成原理，实阵元和虚拟阵元的接收信号线性叠加形成指向性，虚拟阵元信号中的相关噪声和实阵元的非相关噪声叠加，最终阵列噪声仍为个不相关的噪声。回波信号为式(12)中所示，信号的幅值为1，若噪声为平稳信号，则基阵输出端的平均功率为

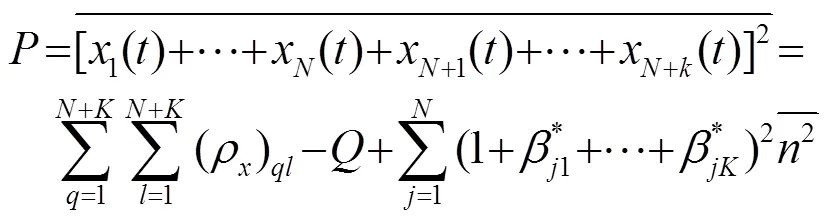
式中前两项为基阵输出信号平均功率，最后一项为基阵输出噪声平均功率。则基阵的输出信噪比为

单个无方向阵元的输入信噪比为

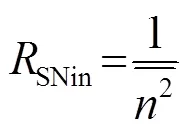
阵增益定义为

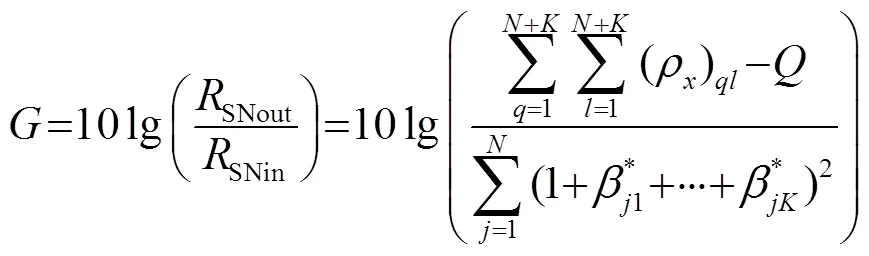
由阵增益可知，当虚拟阵元接收信号估计准确时，式(25)得到最大值。当信号完全相关时，阵增益为

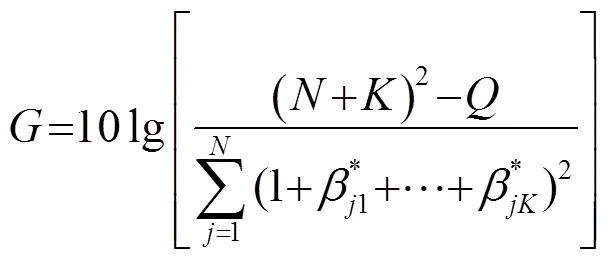
从式(26)可以看出，虚拟阵列输出信噪比的大小主要由的值决定。值表示估计误差，这说明估计算法的准确性与虚拟阵元波束形成的性能紧密相关。从式(25)阵增益表达式上看出，阵增益的大小不仅与估计算法的准确度有关，还与实阵元和虚拟阵元接收信号之间的相关性有关。相关性越强，分子前一部分的值越大，估计信号也越准确，的值也会随之减小，阵增益得到提高。反之，则阵增益逐渐下降。这表明虚拟阵元接收信号的数目存在约束，不能无限制地扩展。

3 计算机仿真

下面通过计算机仿真来验证算法的性能，并与其他相关算法，如常规相移法和文献[10]中的线性预测法、最小二乘法进行比较。仿真中，阵列采用元等间隔均匀线阵，所有阵元各向同性，置于目标回波声场的远场区，阵元间隔=0.01 m，虚拟阵元波束形成方法皆前向构建个虚拟阵元接收信号。回波信号中心频率为100 kHz，入射角度为0，背景为加性高斯限带噪声。

3.1 波束性能及阵增益分析

通过比较最小一乘(LAD)虚拟阵元波束形成与常规相移波束形成的波束图和阵列增益随着虚拟阵元信号数目变化曲线，来验证算法的性能和有效性。图2是在无噪声和有噪声时，16个实阵元采用最小一乘法构建8个虚拟阵元和常规相移法的波束比较图。图2(a)中显示，最小一乘法在理想情况下得到的波束宽度相比相移法明显变窄4o，两种方法形成的旁瓣高度相差不大，第一旁瓣均在-13 dB左右，其他旁瓣高度基本保持在-18 dB附近。图2(b)和图2(c)是将两种方法在回波信号信噪比为-4 dB和4 dB时的比较结果。从比较的波束图中可以看出，在低信噪比的情况下，最小一乘法得到的波束主瓣更窄。由于最小一乘估计的稳健性，所以在信号环境较差的时候依然能估计出较为可靠的值，构建的虚拟阵元接收信号与实际阵元接收信号的误差更小。从图2(b)和图2(c)中可以看出，最小一乘法相比常规相移法在不同信噪比时都能获得较窄的波束，而旁瓣高度两者相差不大。通过上述实验可以看出最小一乘法在低信噪比的环境下仍可得到较窄的波束。

图2 无噪声和有噪声时常规相移和LAD虚拟阵的波束形成图

为了能直观地体现出阵增益的变化规律，在阵增益的实验中将阵元间距增大至0.1 m，信号频率更改为1.5 kHz，实阵列增益曲线的阵元间距设为0.1 m，并与不同阵元间距的虚拟阵列增益的变化曲线进行对比。图3是实阵列增益和虚拟阵列的阵增益随着虚拟阵元信号数目变化的曲线图。虚拟阵列分别设置了3种不同阵元间距：=0.1 m,=0.2 m，=0.3 m。仿真中回波信噪比为0 dB，回波角度0为30o，实阵阵元数为8个，信号脉冲宽度为10 ms。从图3的曲线图中可以看出。选定恰当的虚拟阵元数时，最小一乘法能够得到比较高的阵增益。由式(25)和仿真曲线可以验证，实阵列增益值在上述参数确定后为一固定值。由图3中的阵增益曲线图可以看出，通过构建虚拟阵元可以有效地增加阵增益，但随着构建的虚拟阵元信号数目增加到某一临界值时，阵增益曲线逐渐下降。如阵元间距为0.1 m的阵增益曲线，当虚拟阵元信号数目为45时阵增益达到最高值，随后阵增益开始减少。观察阵元间距和虚拟阵元数目临界值的变化可以看出，增大阵元间距后，虚拟阵元数的临界数减小，这反映了实阵元接收信号与虚拟阵元接收信号之间的相关性与阵元的间距有关，且呈反比关系。

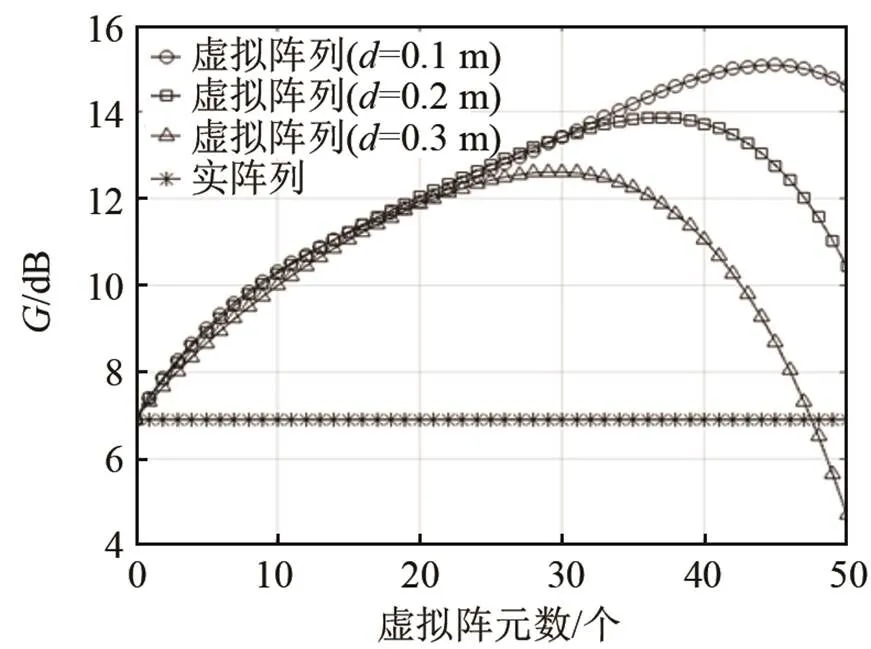
图3 阵增益随着虚拟阵元信号数的变化曲线

3.2 不同方法对比分析

在信噪比为-4 dB、0 dB和4 dB的回波环境下，对比最小一乘(LAD)、最小二乘法和线性预测法3种虚拟阵元波束形成方法的波束图，结果如图4所示。图4(a)～4(c)是三种方法随着信噪比的增加的波束图，随着信噪比的增加，最小一乘法(LAD)和最小二乘法的波束主瓣宽度和旁瓣高度逐渐接近。这是因为最小一乘与最小二乘算法在理论上的估计准则导致的，当回波信噪比较高时，估计结果基本相似。在不同信噪比的环境下，线性预测法的旁瓣高度相比其他两种算法总能保持最低。在低信噪比时，相比其他算法，最小一乘法总能得到较窄的波束，波束指向性和抗干扰能力更好，但旁瓣的高度不如其他两种虚拟阵元波束形成方法的旁瓣低，结果如图4(a)所示。

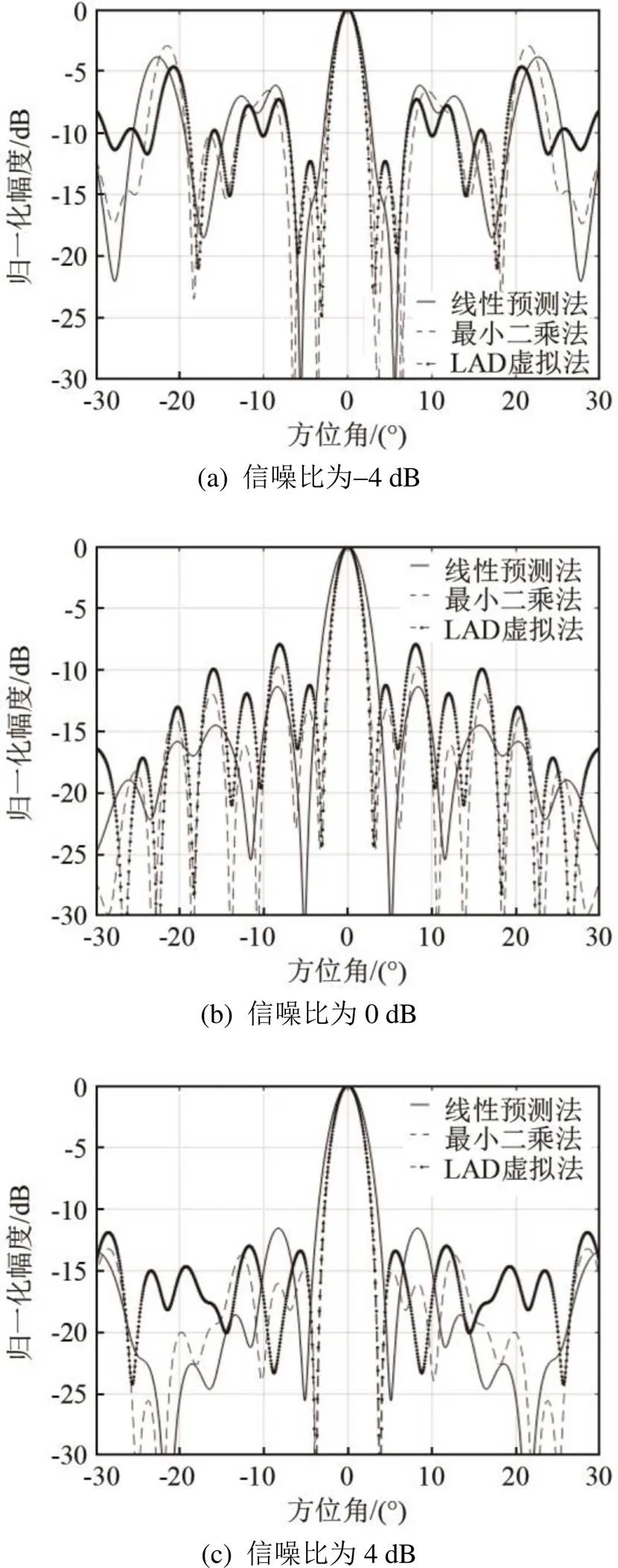
图4 信噪比为4 dB、0 dB和4 dB时LAD法、线性预测法和最小二乘法三3种虚拟阵的波束形成图

通过上述仿真可知，虚拟阵元接收信号估计算法的准确度和实现方式直接影响波束性能。若算法估计误差较大或者在低信噪比的环境中下算法的稳健性较差，则阵列输出波束的形状也会产生明显畸变，波束的性能将受到极大影响。

3.3 多波束性能分析

3.1和3.2节中的波束仿真是在单个波束的情况下，研究了最小一乘虚拟阵元波束形成算法的优缺点。图5是常规相移法与最小一乘法进行多波束仿真的结果。为了研究最小一乘法角度分辨的性能，以波束主瓣在坐标轴上交点之间的夹角为间隔形成三个顺序排列的波束，并与常规相移法进行比较，仿真中采用16个实阵元的线阵并构建8个虚拟阵元接收信号。从图5(a)中可以看出，常规相移法的三个波束主瓣的极大值分别在5o、15o和25o方向上，角度分辨率为10o。图5(b)最小一乘虚拟阵元波束形成方法画出三个波束图，三个波束主瓣的极大值分别出现在5o、12o和19o方向上，角度分辨率为7o。相比常规相移波束形成，最小一乘法的角度分辨率提高了3o。角度分辨率的提升将有利于对目标的识别和成像。如图5(b)所示最小一乘虚拟阵元多波束形成的旁瓣相比常规相移多波束有所升高，主瓣角度附近的旁瓣高度相比常规相移波束形成提高了约3 dB。

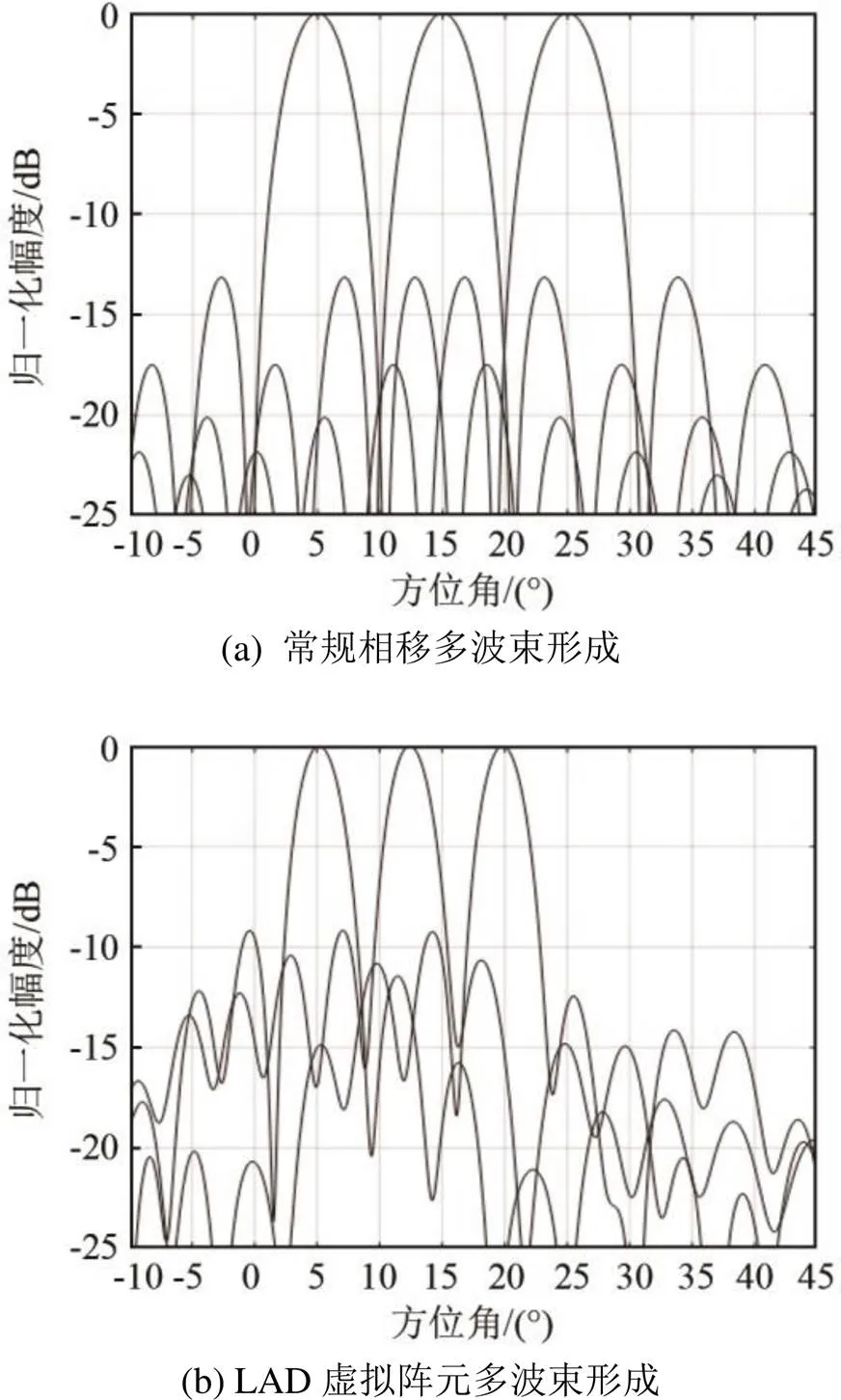
图5 常规相移多波束形成和LAD虚拟阵元多波束形成的波束图

3.4 虚拟阵元数目对波束性能的影响

下面在信噪比为-4 dB、实阵元和观测方程个数确定后，分析波束性能受虚拟阵元数目的影响情况。为了使现象明显，本次仿真实际阵元数为8个，观测方程以1o为间隔在0=0o两侧得到31组方程，其他仿真条件同上，仿真结果如图6所示。

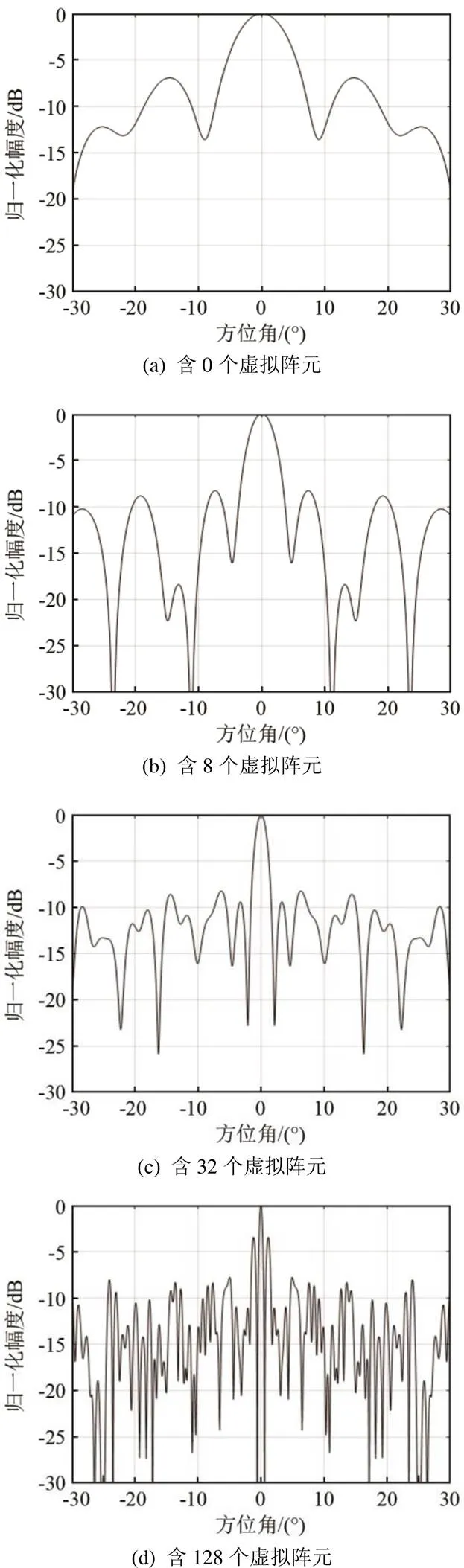
图6 实阵元为8个时含0、8、32和128个虚拟阵元的线阵波束图

从图6中可以看出，增加虚拟阵元接收信号的数目可以明显地提升波束的指向性。仿真中虚拟阵元接收信号个数由0增加到32时，形成的波束主瓣形状逐渐尖锐且宽度逐渐变窄，旁瓣高度逐步降低。但是当虚拟阵元接收信号个数增加至128个时，主瓣两侧的旁瓣高度明显增高，在进行目标方位的判断时会造成模糊。旁瓣高度增加是因为利用最小一乘构建的虚拟阵元接收信号是完全根据真实阵元接收信号构建的，虚拟阵元数目的不断增加，虚拟阵元接收信号与实际接收信号之间的相关性开始减弱，估计的误差逐渐增大，导致波束的形状发生畸变。以上结果也与图3中曲线的变化相统一，当构建的虚拟阵元接收信号数目达到临界值时，阵增益开始下降，波束的性能也开始变差。若虚拟信号数目大于临界值时，波束性能将不能有效提升，因此虚拟阵元接收信号数目不能无限制地增加。

4 结论

对虚拟阵元接收信号的估计构建是虚拟阵元波束形成算法的关键，估计算法直接影响波束形成的性能。本文研究了现有虚拟阵元波束形成方法构建虚拟阵元接收信号的区别，提出了一种基于最小一乘稳健估计的波束形成方法，该方法在低信噪比的环境下构建的虚拟阵元接收信号更加准确、稳健。

相比其他虚拟阵元波束形成方法，本文方法形成的波束抗干扰能力更强且波束宽度更窄。该方法形成多波束时，可在不增加基阵孔径的同时得到的较高的角度分辨率，这将有利于成像声呐的目标识别。从理论分析和实验仿真都可看出，虚拟阵列比实际阵列可以获得更高的阵增益。在实际中，噪声并非理想加性高斯限带噪声且信噪比往往较低，波束形成方法抗干扰的能力尤为重要，因此本文提出的最小一乘虚拟阵元波束形成在-4 dB 这样较低信噪比的情况下更具优势。

[1] XIA W J, JIN X, DOU F W. Thinned array design with minimum number of transducers for multi-beam imaging sonar[J]. IEEE Transactions on Oceanic Engineering, 2017, 42(4): 892-900.

[2] BROWN C J, BLONDEL P. Developments in the application of multibeam sonar backscatter for seafloor habitat mapping[J]. Applied Acoustics, 2009, 70(10): 1242-1247.

[3] FONSECA L, MAYER L. Remote estimation of surficial seafloor properties through the application angular range analysis to multibeam sonar data[J]. Marine Geophysical Researches, 2007, 28(2): 119-126.

[4] de MOUSTIER C, LONSDALE P F, SHOR A N. Simultaneous operation of the sea beam multibeam echo-sounder and the seaMARC II bathymetric sidescan sonar system[J]. IEEE Transactions on Oceanic Engineering, 1990, 15(2): 84-94.

[5] CHO H, KIM B, YU S C. AUV-based underwater 3-D point cloud generation using acoustic lens-based multibeam sonar[J]. IEEE Transactions on Oceanic Engineering, 2017, 43(4): 856-872.

[6] XU C, LI H, CHEN B, WANG X. Angular response classification of multibeam sonar based on multi-angle interval division[C]//IEEE/OES China Ocean Acoustics (COA), Harbin, China: IEEE, 2016: 1-4.

[7] XU W, SHI H，ZHANG H. Sparse-reconstruction-basedhigh resolution beamforming and its application to multi-beam systems[C]//2012 Oceans–Yeosu, Yeosu, Korea (south): IEEE, 2012: 1-4.

[8] 倪淑燕, 程乃平, 倪正中. 共轭虚拟阵列波束形成方法[J]. 电子学报, 2011, 39(9): 2120-2124.

NI Shuyan, CHENG Naiping, NI Zhengzhong. Conjugate virtual array beamforing methed[J]. Acta Electronica Sinica, 2011, 39(9): 2120-2124.

[9] 胡鹏. 虚拟阵元波束形成方法研究[D]. 西安: 西北工业大学, 2006.

HU Peng. Study on beamforing algorithm of array with virtual elements[D]. Xi’an: Northwestern Polytechnical University, 2006.

[10] 陈欢, 杨德森, 张揽月, 等. 基于遗传算法的声矢量阵虚拟阵元波束形成[J]. 信号处理, 2009, 25(10): 1498-1501.

CHEN Huan, YANG Desen, ZHANG Lanyue, et al. Virtual array beam forming algorithm based on genetic algorithm of vector hydrophones[J]. Signal Processing, 2009, 25(10): 1498-1501.

[11] 陈希孺. 最小一乘线性回归(上)[J]. 数理统计与管理, 1989(5): 48-55.

CHEN Xiru. Least absolute deviation regression(vol. 1 of 2)[J] Journal of applied statistics and management, 1989(5): 48-55.

[12] LI Y B, ARCE G R. A maximum likelihood approach to least absolute deviation regression[J]. EURASIP Journal on Advances in Signal Processing, 2004(12): 1762-1769.

[13] 王福昌, 胡顺田, 张艳芳. 最小一乘回归系数估计及其MATLAB实现[J]. 防灾科技学院学报, 2007(4): 85-89.

WANG Fuchang, HU Shuntian, ZHANG Yanfang. The coefficient estimation of least absolute deviation regression and implementation in MATLAB[J]. Journal of Institute of Disaster-Prevention Science and Technology, 2007(4): 85-89.

[14] 陈希孺. 最小一乘线性回归(下)[J]. 数理统计与管理, 1989(6): 48-56.

CHEN Xiru. Least absolute deviation regression(2 of 2)[J]. Journal of Applied Statistics and Management, 1989(6): 48-56.

[15] 李贵斌. 声呐基阵设计原理[M]. 北京: 海洋出版社, 1993.

LI Guibin. The principle of sonar array design[M]. Beijing: China Ocean Press, 1993.

Simulation of virtual array beamforming based on least absolute deviation

ZHANG Weimin1, GUO Haitao2, JIN Qiyu3, TIAN Yuanyuan4, JIAO Shengxi5

(1. College of Electronic Information Engineering, Inner Mongolia University, Hohhot 010021, Inner Mongolia, China; 2. School of Marine Information Engineering, Hainan Tropical Ocean University, Sanya 572022, Hainan, China; 3. School of Mathematical Sciences, Inner Mongolia University, Hohhot 010021, Inner Mongolia, China; 4. School of Mechanical Engineering, Northeast Dianli University, Jilin 132012, Jilin, China; 5. College of Automation Engineering, Northeast Dianli University, Jilin 132012, Jilin, China)

The quality of beamforming is the key to the imaging quality of underwater multi-beam imaging system. When the signal frequency is constant, the conventional phase-shifting beamforming algorithm can only get a narrower beam by increasing the aperture of the array, but this method is restricted by practical conditions in engineering. Therefore, a virtual array beamforming algorithm based on least absolute deviation (LAD) estimation is presented, by which a narrower and more robust beam can be obtained without increasing the array size, moreover the array gain and the angle resolution of sonar image can be increased under low signal to noise ratio (SNR). The superiority of the above method is verified by using Matlab simulation and comparing with other methods.

multi-beam imaging system; least absolute deviation estimation; robustness; virtual array; beamforming

TN911.7

A

1000-3630(2020)-02-0134-07

10.16300/j.cnki.1000-3630.2020.02.002

2018-10-04;

2018-12-17

国家自然科学基金(61661038，41076060)、内蒙古自然科学基金(2014MS0601)资助项目

张伟民(1993－), 男, 内蒙古包头人, 硕士研究生, 研究方向为信号处理。

郭海涛,E-mail: ghtpaper@126.com