VMD-Hilbert变换在扬声器异常声检测中的应用

周静雷，颜婷，房乔楚

VMD-Hilbert变换在扬声器异常声检测中的应用

周静雷，颜婷，房乔楚

(西安工程大学电子信息学院，陕西西安 710600)

针对基于时频分析的扬声器异常声检测方法中短时傅里叶变换、小波包变换存在的不足，提出了一种基于变分模态分解-希尔伯特(Variational Mode Decomposition and Hilbert, VMD-Hilbert)变换的扬声器异常声检测方法。首先通过仿真信号分析，研究了VMD-Hilbert变换的时频特性，并与其他三种时频分析进行了对比，结果表明VMD-Hilbert变换具有更好的自适应性、能量聚焦性与时频分辨率。然后，对实测扬声器声响应信号进行VMD-Hilbert变换，求得被测扬声器单元的时频矩阵与标准时频矩阵之间的特征距离，并与其它三种时频分析下的特征距离进行对比。实验结果表明，VMD-Hilbert变换下的类间特征距离的离散度较大，便于更好地设定阈值，从而验证了VMD-Hilbert变换能更好地表征异常声的时频特征，以及其在处理非线性、非平稳的扬声器声响应信号时的优越性。

扬声器异常声检测；时频分析；变分模态分解；Hilbert变换；特征距离

0 引言

无论是在扬声器的设计、生产阶段，还是维护阶段，异常声检测都是一个至关重要的环节，尤其是现今人们对听音品质的要求越来越高。人工听音虽对扬声器潜在故障较为敏感，但受听音员的主观因素影响较大，难以做到检测结果的重现性和可比性[1]。扬声器异常声检测的自动化、快速化、高灵敏度以及检测结果的高准确性，一直是国内外广大扬声器异常声检测研究者所追求的。

扬声器检测时的声响应信号是非线性、非平稳的声频信号[2]，其时域特征较为微弱[3-4]，难以被检测，若只进行频域特征检测，又会损失振动特征，因此利用时频分析的方法来检测扬声器异常声是一种更为有效的方法。Davy等[5]利用科思(Cohen)类时频分析的方法，得到声响应信号的时频矩阵，然后计算科尔莫洛夫(Kolmogorov)距离来实现扬声器的异常声检测。Brune等[6]利用短时傅立叶变换对扬声器声响应信号进行时频分析，发现合格扬声器的时频图中只有基波和少量的低阶谐波出现，而故障扬声器具有较宽的频谱。Ruiz等[7]对所测得的扬声器工作时两端的电流信号进行赵-阿特拉斯-马克斯分布(Zhao-Atlas-Marks Distribution, ZAMD)变换，再对获得的时频图进行分割，求取与正常扬声器时频图之间的马氏距离，实验表明，随着扬声器故障程度的加深，对应的马氏距离也在增加。

在国内，于德敏等[8]从图像的角度，研究了不同故障扬声器在短时傅里叶变换、小波包变换下的3种特征距离，实现了扬声器异常声的检测。李宏斌等[9]将经短时傅里叶变换后获得的时频图进行分割，并计算与黄金样品对应矩阵的Kolmogorov距离，从而判断扬声器是否存在异常声。李云红等[10]利用希尔伯特黄变换(Hilbert Huang Transform, HHT)对建立的几种扬声器异常声模型进行了分析，得出不同的异常声种类，其Hilbert谱呈现出不同的特征规律。周晓东等[11]研究了短时傅里叶变换下，不同窗函数对扬声器异常声检测的影响，确定所研究的8种窗函数中，最佳窗函数为平顶窗。

在基于时频分析的扬声器异常声检测中，相关学者主要采用了短时傅里叶变换(Short-Time Fourier Transform, STFT)与小波包变换(Wavelet Packet Transformation, WPT)，其中WPT所选择的小波函数主要为dmey小波，分解层数为6层，但并没有对不同的时频分析方法进行对比分析。STFT与WPT在分析非线性、非平稳信号时，都具有一定的局限性。STFT虽在一定程度上克服了傅里叶变换不具备局部分析能力的缺陷，但它实际上是一种单一分辨率的变换，即窗函数一旦确定，时频分辨率也随之确定。WPT虽具有多分辨率的特点，但它实质上是一种窗口可调的傅里叶变换，仍受测不准原理的限制，且存在能量泄露、小波函数以及分解层数难以选择的问题，不具有良好的自适应性。而经验模态分解(Empirical Mode Decomposition, EMD)在处理非线性、非平稳信号时虽具有自适应性，但其本质上属于递归式模态分解，包络估计误差经多次递归分解而被放大，易出现模态混叠，且其频率分辨率受限，分解结果受采样率的影响较大[12]。

针对EMD存在的问题，Dragomiretskiy等[13]提出了一种非递归式的、自适应的、具有多分辨率的信号分解方法——变分模态分解(Variational Mode Decomposition, VMD)。VMD在很大程度上克服了EMD的模态混叠、误差累积等问题[14-15]，其本质上是一系列自适应的维纳滤波器，具有很好的噪声鲁棒性。贾亚飞等[16]利用VMD-WVD联合分析高压电器设备局部放电信号，有效地解决了Wigner-Ville分布的交叉项干扰问题，并保证了较高的能量聚集性和很好的时频分辨率。向玲等[17]利用VMD-Hilbert变换与HHT处理转子故障信号，实验结果表明，VMD-Hilbert变换更能准确地提取出转子故障特征。VMD已经在处理非线性、非平稳故障信号中得到了广泛的应用，并能很好地提取故障特征。

针对STFT、WPT方法在处理非线性、非平稳信号时的局限性，以及EMD存在的模态混叠等问题，本文首次将VMD-Hilbert变换应用于扬声器的异常声检测中。首先，基于仿真信号，对STFT、WPT、HHT、VMD-Hilbert变换的时频特性展开了对比研究。然后，在实测信号的基础上，对实测信号进行时频变换，求得几种不同时频变换下的特征距离，对比分析了特征距离之间的离散度，以期为扬声器异常声检测引入一种新的、有效的时频分析方法，提高检测的准确率。

1 理论分析

1.1 变分模态分解

VMD以各模态带宽和最小为原则，采用乘法算子交替方向法(Alternate Direction Method Multiplires, ADMM)，将复杂信号分解成具有有限带宽的一系列调幅调频信号，即变分模态函数(Variational Mode Function, VMF)，且所有分量满足固有模态函数(Intrinsic Mode Function, IMF)的定义。

1.1.1 变分问题的构建

最后，通过L2范数梯度的平方估计出各个模态的带宽，构建出如下变分约束问题：

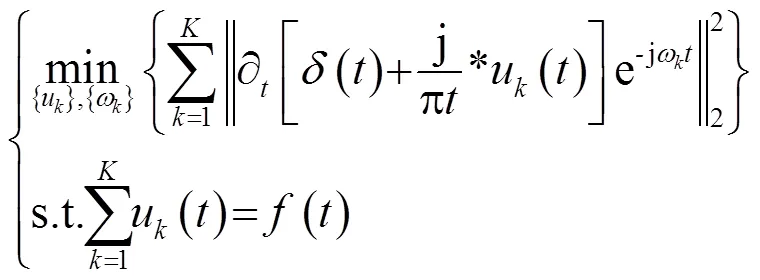
1.1.2 变分问题的求解

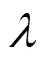
式(3)的增广拉格朗日函数为

从而式(3)的最小值优化问题转变成了式(4)中求一系列迭代子优化中的增广拉格朗日函数的鞍点问题，即ADMM。

VMD中的ADMM优化算法步骤：

(2) 迭代循环=+1；

(5) 直到满足收敛条件：

1.2 特征距离计算

由于Kolmogorov距离具有良好的归一化特性以及计算速度快的特点[9]，本文采用Kolmogorov特征距离，其计算过程如下：

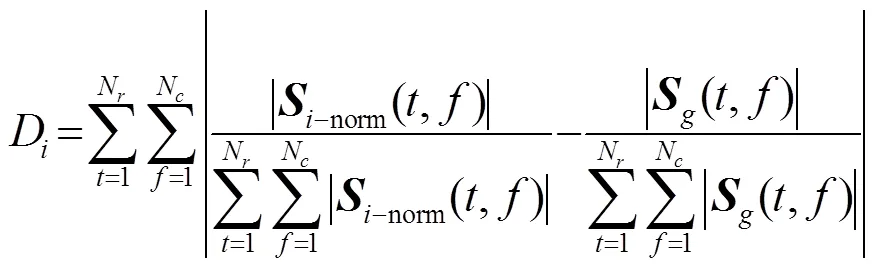
2 仿真信号分析

为研究VMD-Hilbert变换、HHT、WPT、STFT的时频特性，构造如式(11)所示的仿真信号：

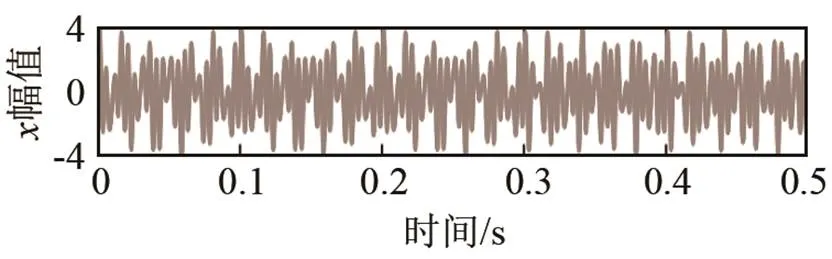
图1 仿真信号及其各分量时域图

表1 仿真信号不同值对应的中心频率 (Hz)

图2 VMD分解后各模态时域图

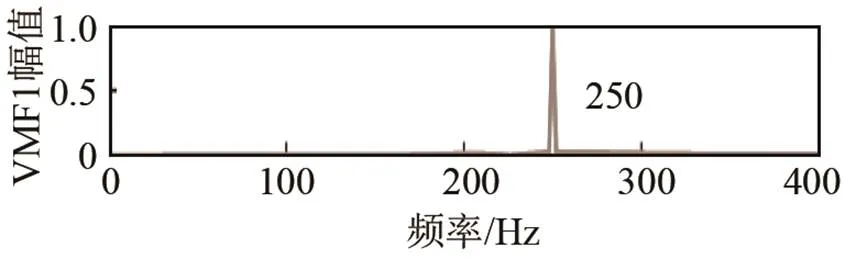
图3 VMD分解后各模态频谱图

图4 仿真信号的VMD-Hilbert时频谱

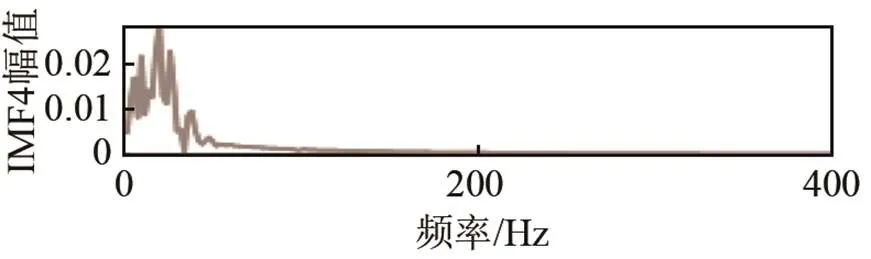
图7 仿真信号的HHT时频谱

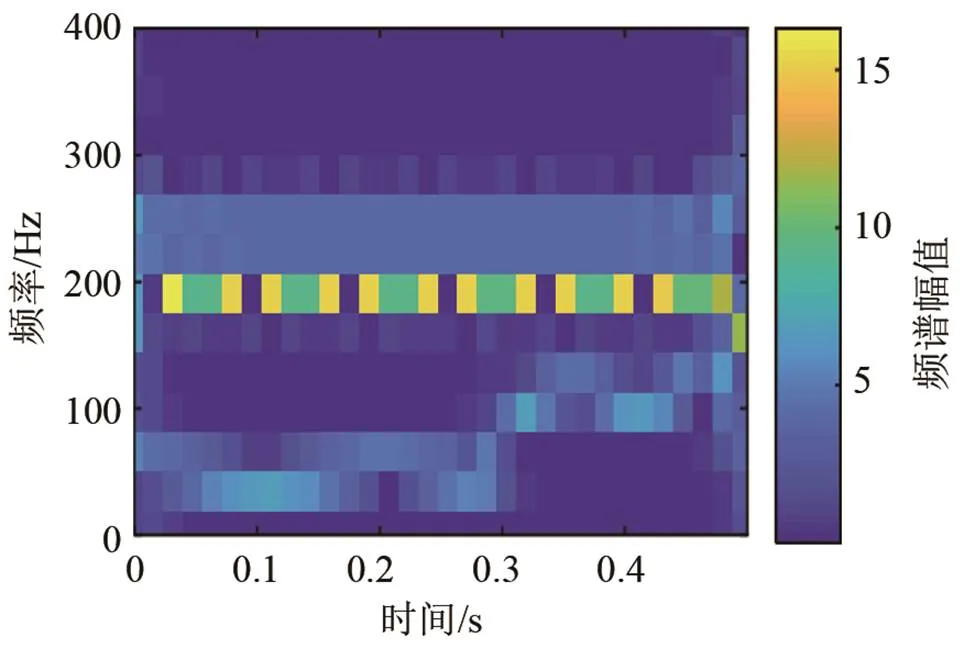
图8 仿真信号的6层WPT时频谱

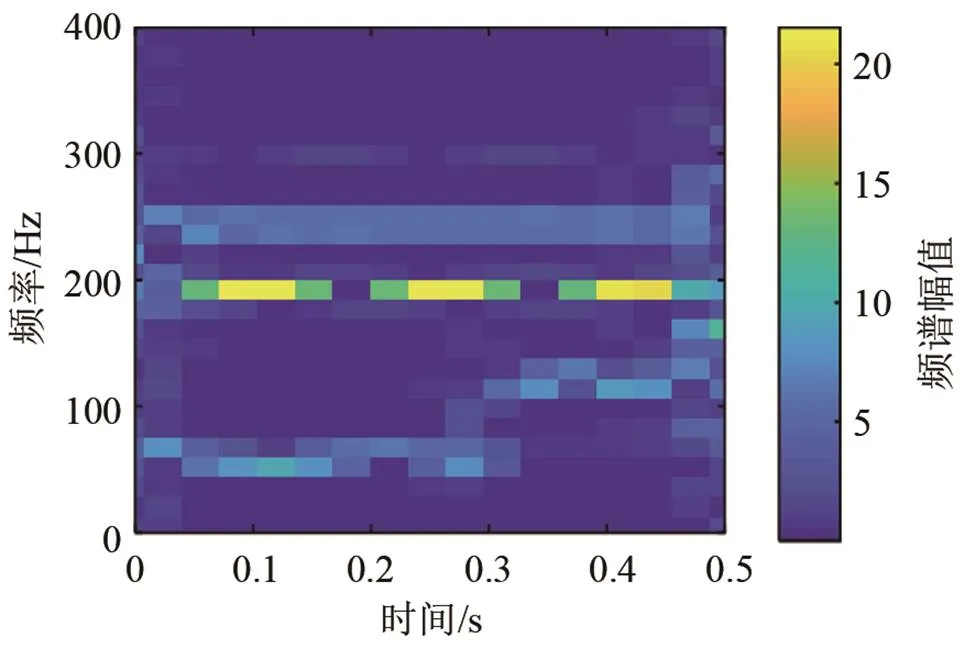
图9 仿真信号的7层WPT时频谱

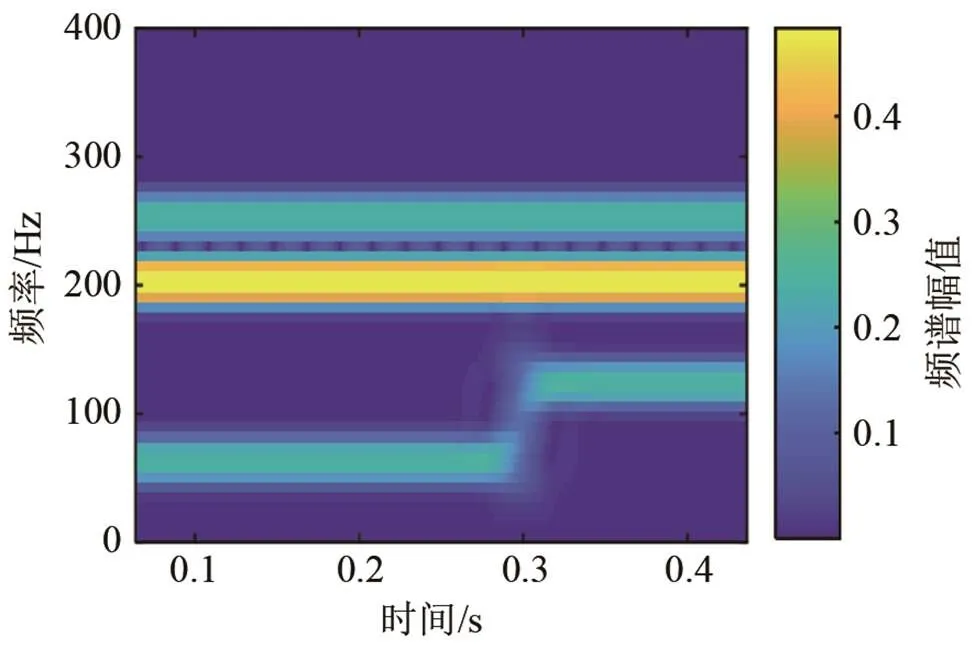
图10 仿真信号的STFT时频谱(平顶窗、窗长512)

综上所述，VMD-Hilbert变换具有更好的自适应性、能量聚焦性与时频分辨率，而EMD存在模态混叠现象，WPT、STFT都受测不准原理的限制，难以兼顾时频分辨率。

图11 仿真信号的STFT时频谱(平顶窗、窗长1 024)

3 实测信号分析

3.1 实验测量

为分析VMD-Hilbert变换、HHT、WPT、STFT4种不同的时频分析方法对异常声检测的影响，设计了如下测量实验：测量对象为32个1511型微型扬声器单元，编号为1～32号，其中1～13号为良品，14～32号为不良品。该款扬声器单元的谐振频率为1 000 Hz。相对于从低频到高频扫描的方式，从高频到低频扫描的方式，可减小扬声器单元测量时的稳定时间[18]，而异常声主要出现在谐振频率附近，因此，本实验采用频率为10 000～100 Hz的连续对数扫频信号激励被测扬声器单元。测量原理如图12所示。

图12 实验测量原理图

3.2 数据处理与分析

下面通过对比不同时频分析方法下的特征距离的离散度，来验证VMD-Hilbert变换时频分析方法在处理非线性、非平稳的扬声器响应信号时的有效性。

依据前人的研究，本实验选取dmey小波对扬声器声响应信号进行6层小波包分解[7]；STFT的窗函数选择窗长为1 024的平顶窗[11]。依据上述方法求取4种不同时频分析下的Kolmogorov距离，其分布图如图13所示。纵坐标的1、2、3、4分别代表VMD-Hilbert变换、HHT、WPT、STFT。

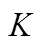
表2 实测信号不同值对应的中心频率 (Hz)

图13 4种时频分析下的Kolmogorov距离分布图

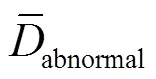
由图13和表3可知，良品与不良品在HHT下的Kolmogorov距离出现了混淆，无法完全区分良品与不良品；VMD-Hilbert变换下的类间Kolmogorov距离离散度最大，便于更好地设定阈值，以区分良品与不良品，而WPT、STFT下的类间Kolmogorov距离离散度相对较小，这也验证了VMD-Hilbert变换在处理非线性非平稳扬声器响应信号时的有效性，而WPT、STFT受测不准原理的限制，在处理非线性、非平稳信号时具有一定的局限性。

表3 4种时频分析下的

4 结论

本文首次将一种新的时频分析方法VMD-Hilbert变换应用于扬声器的异常声检测中，结论如下：

(1) 通过仿真信号分析得出：VMD能自适应地将多频率分量分解到多个模态中，克服了EMD中的模态混叠现象，相较于STFT、WPT、HHT，VMD-Hilbert变换具有更好的时频分辨率、能量聚集性与自适应性。

(2) 通过实测扬声器声响应信号分析得出：与STFT、WPT、HHT相比，VMD-Hilbert变换下的类间特征距离离散度较大，能更好地设定阈值，更有利于实现扬声器异常声检测。实验结果表明，VMD-Hilbert变换能更好地表征扬声器异常声在时频域上的特征。

[1] STEFAN I, KLIPPEL W. Fast and sensitive end-of-line testing[C]//Audio Engineering Society Convention 144. Audio Engineering Society, 2018: 9927-9937.

[2] NOVAK A, SIMON L, KADLEC F, et al. Nonlinear system identification using exponential swept-sine signal[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(8): 2220-2229.

[3] STEVE T, PASCAL B. Enhancements for loose particle detection in loudspeakers[C]//Audio Engineering Society Convention 116, 2004: 6164-6175.

[4] IRRGANG S, KLIPPEL W, SEIDEL U. Loudspeaker testing at the production line[C]//Audio Engineering Society Convention 120, 2006: 6845-6858.

[5] DAVY M, DONCARLI C. A new nonstationary test procedure for Improved Loudspeaker Fault Detection[J]. Journal of the Audio Engineering Society, 2002, 6: 458-469.

[6] BRUNET P, CHAKROFF E, TEMME S. Loose particle detection in loudspeakers[C]//Audio Engineering Society Convention 115, 2003: 5883-5893.

[7] RUIZ I G, SALA C V, DELGADO P M, et al. Loudspeaker Rub fault detection by means of a new nonstationary procedure test[C]//Audio Engineering Society Convention 129, 2010: 8283-8290

[8] 于德敏, 李小明, 许增朴. 基于时频分析的扬声器异音故障诊断方法[J]. 电声技术, 2007, 31(11): 24-27.

YU Demin, LI Xiaoming, XU Zengpu. Loudspeaker fault diagnosis method based on time-frequency transform of acoustic signal[J]. Audio Engineering, 2007, 31(11): 24-27.

[9] 李宏斌, 徐楚林, 温周斌. 基于短时傅里叶变换的异常音检测方法[J]. 声学技术, 2014, 33(2): 145-149.

LI Hongbin, XU Chulin, WEN Zhoubin. A STFT based method for detecting Rub & Buzz defects of loudspeaker and its application research[J]. Technical Acoustics, 2014, 33(2): 145-149.

[10] 李云红, 李小英, 周静雷, 潘杨. 基于HHT算法的扬声器异常音检测技术[J]. 计算机工程与应用, 2015, 51(11): 212-217.

LI Yunhong, LI Xiaoying, ZHOU Jinglei, et al. Loudspeaker detection technology based on HHT algorithm[J]. Computer Engineering and Applications, 2015, 51(11): 212-217.

[11] 周晓东, 沈勇, 薛政, 等. 窗函数在扬声器异常声客观检测中的影响[J].应用声学, 2018, 37(3): 373-377.

ZHOU Xiaodong, SHEN Yong, XUE Zheng, et al. The selection of window functions in loudspeaker Rub & Buzz detection[J]. Journal of Applied Acoustics, 2018, 37(3): 373-377.

[12] LIU T, LUO Z J, HUANG J H, et al. A comparative study of four kinds of adaptive decomposition algorithms and their applications[J]. Sensors, 2018, 18(7): 2120-2171.

[13] DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544.

[14] ZAROUR D, MEZIANI S, KEDADOUCHE M, et al. Faulty bearing features by variational mode decomposition[J]. Vibroengineering PROCEDIA, 2017, 16: 29-34.

[15] GUO Y F, ZHANG Z S, GONG T, et al. Generalized variational mode decomposition for interlayer slipping detection of viscoelastic sandwich cylindrical structures[J]. Measurement Science and Technology, 2018, 29(9): 1-24.

[16] 贾亚飞, 朱永利, 王刘旺. 基于VMD和Wigner-Ville分布的局放信号时频分析[J]. 系统仿真学报, 2018, 30(2): 569-578.

JIA Yafei, ZHU Yongli, WANG Liuwang, Time-frequency analysis of partial discharge signal based on VMD and Wigner-Ville distribution[J]. Journal of System Simulation, 2018, 30(2): 569-578.

[17] 向玲, 张力佳. 变分模态分解在转子故障诊断中的应用[J]. 振动、测试与诊断, 2017, 37(4): 793-799, 847.

XIANG Ling, ZHANG Lijia. Application of variational modal decomposition in rotor fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosi, 2017, 37(4): 793-799, 847.

[18] TEMME S, DOBOS V. Evaluation of audio test methods and measurements for end-of-line automotive loudspeaker quality control[C]//Audio Engineering Society Convention 142, 2017: 1-10.

The application of VMD-Hilbert transform in loudspeaker Rub & Buzz detection

ZHOU Jinglei, YAN Ting, FANG Qiaochu

(School of Electronics and Information, Xi’an Polytechnic University, Xi’an 710048, Shaanxi, China)

In view of the shortcomings of loudspeaker Rub & Buzz detection based on time-frequency analysis, such as short-time Fourier transform and wavelet packet transform, a method of loudspeaker Rub & Buzz detection based on variational mode decomposition and Hilbert (VMD-Hilbert) transform is proposed. Firstly, the time-frequency characteristics of the VMD-Hilbert transform are studied by simulation signal analysis, and compared with the other three time-frequency analysis methods. The results show that the VMD-Hilbert transform has better adaptability, energy focus and time-frequency resolution. Then, the sound response signals of measured loudspeakers are processed with VMD-Hilbert transform to obtain the feature distances between the measured loudspeakers. The comparative analysis of feature distances obtained by different time-frequency analysis methods is made. The experimental results show that the dispersion of the feature distances between classes under VMD-Hilbert transform is larger, which is beneficial for setting the appropriate threshold. It is verified that the VMD-Hilbert transform can better represent the time-frequency characteristics of Rub & Buzz, and its superiority in dealing with nonlinear and nonstationary loudspeaker sound responses is also verified.

loudspeaker Rub & Buzz detection; time-frequency analysis; variational mode decomposition; Hilbert transform; feature distance

TN912

A

1000-3630(2020)-02-0200-08

10.16300/j.cnki.1000-3630.2020.02.013

2019-04-15;

2019-06-15

周静雷(1978－), 男, 陕西西安人, 博士, 研究方向为嵌入式，电声学。

颜婷,E-mail: yantingannie@163.com