应用非线性Lamb波识别三维铝板中的微裂纹方向的研究

祝伟光，关立强，李义丰

应用非线性Lamb波识别三维铝板中的微裂纹方向的研究

祝伟光，关立强，李义丰

(南京工业大学计算机科学与技术学院，江苏南京 211800)

针对结构中不同裂纹方向的检测问题，采用数值模拟的方法，通过有限元软件ABAQUS建立了一种包含人工粘弹性吸收边界的三维铝板模型，对Lamb波S0模态信号与微裂纹的非线性关系进行研究。在该模型中，将三维埋藏微裂纹嵌入到模型内部的固定位置，在相同激励条件下改变裂纹方向并对仿真获得的时域信号进行频谱分析，然后对不同裂纹方向的二次谐波与基波信号的幅值比指向性图的变化规律进行了比较和讨论。仿真结果表明，不同方向的裂纹对Lamb波在裂纹区的散射场分布有明显的影响，波的传播路径满足反射定律，且前向散射信号的幅值比普遍大于后向散射的幅值比。加上人工吸收边界后，前向散射与后向散射的幅值比差值随着裂纹方向角度的增大而增大。检测结果表明，该方法可以在误差允许范围内对任意裂纹方向的角度进行识别。

非线性Lamb波；三维埋藏裂纹；微裂纹方向；吸收边界；幅值比

0 引言

板状结构在船舶工业、汽车工业、桥梁建筑等工程领域中应用十分普遍。在长期的使用过程中，板状构件受到外力冲击、高压振动、化学腐蚀、热疲劳等各种因素的影响，极容易产生缺陷、裂纹、通孔等损伤，对结构的危害性很大，甚至会诱导灾难性的后果。因此板状构件的结构健康监测(Structural Health Monitoring, SHM)对预防和避免事故的发生有很重要的意义[1-2]。

无损检测(Non-destructive Testing, NDT)凭借高效性和实时性成为SHM系统中不可替代的检测手段[3]。NDT包括多种常规检测方法，由于超声波具有穿透能力强、灵敏度高、无污染的优点，使得超声检测的使用最为广泛[4]。在厚度较薄的薄板结构中传播的波称为Lamb波，与传统的超声导波相比，Lamb波凭借在薄板结构中传播时衰减小和传播距离长的优点被广泛应用在板状结构和壳体结构的损伤检测中[1-2]。

线性Lamb波对尺寸远小于检测声波波长的早期疲劳微裂纹的敏感度较低[2]，而非线性Lamb波信号对由结构内微裂纹引起的反射、散射等物理现象更为敏感[5]，因此非线性Lamb波的NDT研究得到了越来越多的关注[6]。非线性超声检测可以分为高次谐波技术[6]、次谐波技术[7]、非线性共振超声波谱技术[8]、混频技术[9]等。其中，谐波检测在非线性超声检测中应用最为广泛。

近年来，国内外研究人员利用非线性Lamb波谐波法对结构微裂纹进行了大量效果显著的研究[10-12]。Zhou等[10]通过对超声非线性的实验研究，证明了高次谐波可以用来评估疲劳裂纹。Wang等[11]使用非线性Lamb波检测钢板和碳纤维增强塑料(Carbon Fiber Reinforced Plastic, CFRP)加固钢板的疲劳裂纹，通过数值仿真和实验研究，发现二次谐波可以有效识别疲劳裂纹。Yelve等[12]利用非线性Lamb波实现对复合材料层合板的分层缺陷的检测。这些研究都说明了通过对仿真实验过程中携带裂纹信息的谐波进行分析，非线性Lamb波可以实现对微裂纹的损伤检测。但是，目前只有少数研究人员对裂纹的方向角度进行检测，也鲜有学者对不同角度的裂纹对结构的稳定性带来的影响进行深入的探究。其中，Lu等[13]通过对反射系数和透射系数进行分析，发现小尺寸裂纹对入射波角度更敏感，并且评估了裂纹方向对Lamb波在铝板中传播的影响。焦敬品等[14]通过数值仿真分析了超声波与不同方向微裂纹的非线性相互作用。这些研究都是基于二维模型展开的裂纹方向检测，而对于三维(Three-dimensional, 3D)埋藏微裂纹方向的识别研究还没有涉及到。

本文通过3D有限元数值仿真，对非线性Lamb波S0模态信号与结构内部的不同方向微裂纹的相互作用进行了相关研究。对初始模型仿真后，通过快速傅里叶变换(Fast Fourier Transform, FFT)分析接收信号的二次谐波幅值比分布规律。之后在初始模型周围加上吸收边界使反射波的影响降到最低，再分析和比较两种模型的幅值比指向性图的变化趋势，以完成对埋藏微裂纹的方向识别。

1 非线性Lamb波基本理论

Lamb波是超声波在固体板中经上下边界来回反射形成的一种应力波[15-16]。应用在NDT领域时，Lamb波与缺陷损伤相互作用引起的非线性效应来源于两个方面：一是两者接触界面的弹性不对称，表现为应力-应变关系的非线性；二是由于Lamb波传播的影响，裂纹面受到拉伸-挤压而不断振动使响应信号产生滞回效应。

Lamb波在板内传播到非线性区域时，会产生高次谐波，其产生机理与材料的非线性弹性行为有关。根据经典非线性理论，在有限振幅激励条件下，材料中的应力与应变的关系是非线性的，对于一维情况，可以用非线性Hooke定律[17]表示：

超声波遇到闭合微裂纹、分层等接触类损伤时，会出现无法用传统线性理论解释的高次谐波等非线性现象，于是接触非线性的超声理论就逐渐发展起来了。这种接触非线性反映了材料局部的非线性特征，相关的物理模型通常涉及裂纹面的接触、摩擦、裂纹尖端的塑性等，这些非线性源的存在使超声波在传播时与其相互作用后发生强非线性失真，从而产生高次谐波。国内外学者将这种由微裂纹产生的高次谐波响应称为接触声非线性(Contact Acoustic Nonlinearity, CAN)[11, 17-18]现象。

CAN现象产生的物理机制是当超声波到达一个有裂纹的接触面时，裂纹被纵波不停地拉伸和挤压造成裂纹面的反复振动，裂纹在波的压缩阶段闭合，未受干扰的波可以通过裂纹继续传播，而裂纹在波的拉伸阶段张开，部分波的反射影响了波的传播[18]。这种因为超声波的传播而使裂纹面不断接触的现象也称为CAN效应，其示意图如图1所示，波在通过裂纹区后表现为半波整流，呈现出明显的非线性特征，导致了高次谐波的产生[11]。

本文研究的固体介质为薄铝板，其结构内部的微裂纹非线性超声检测问题属于接触非线性的范畴。因此，可以根据检测到的响应信号中是否存在二次谐波或高次谐波来评估结构内部的微裂纹等非线性源。

图1 声接触非线性效应示意图

2 3D有限元仿真

2.1 有限元模型

使用有限元软件ABAQUS建立三维有限元模型，通过显式动力学分析法对非线性Lamb波在铝板中的传播进行仿真。

2.1.1 初始模型

模型尺寸与铝板材料参数如表1所示。在板面的正中心上下两点沿离面方向施加对称应力载荷，产生沿轴方向对称传播的纵波，形成单S0模态信号。仿真时所用信号源激励为450 kHz的汉宁(Hanning)窗调制5个周期的正弦波信号，波形和频谱如图2所示。裂纹中心位置在激励点轴负方向80 mm处，裂纹类型为分层缺陷，用长为2 mm、高为1.2 mm的Cohesive界面单元来嵌入到模型内部创建埋藏微裂纹模型，裂纹长度方向即为模型轴方向。接收点是以裂纹中心为圆心、半径为40 mm的等角度接收阵列，每个相隔30°，分别为1,2,3, ...,12共12个接收点，如图3所示。

Cohesive界面单元可以理解为一种准二维单元，将它看作被一个厚度隔开的两个面，这两个面分别和其他实体单元连接。在预定的裂纹区创建Cohesive单元时，在相同的位置就会有重复的节点编号，当施加的力达到单元强度的临界值时，Cohesive单元从产生损伤到最后失效可以表征结构分层破坏模式，达到模拟分层缺陷的效果。包含cohesive单元的模型单独创建后嵌入到主板模型，并与之建立绑定约束，接触类型为硬接触、无摩擦。

表1 模型尺寸与铝板材料参数

图2 铝板模型激励信号

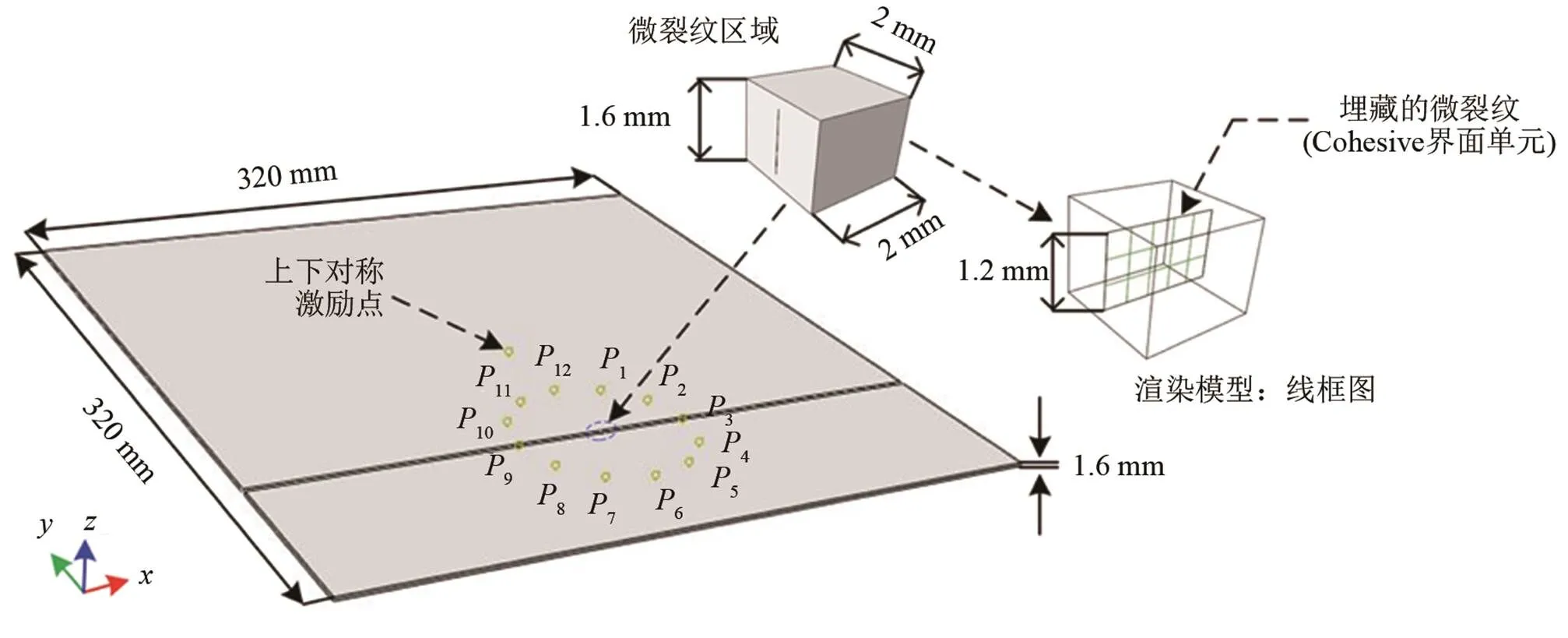
图3 铝板3D模型尺寸及损伤模式示意图

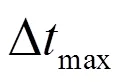
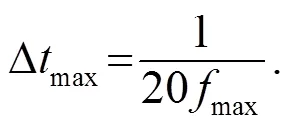
2.1.2 吸收边界模型

为了降低端面反射波对接收信号的影响，在模型的四周添加吸收边界[19]和等效三维一致粘弹性人工边界组合的混合边界单元模型[20]，以达到分析的目的。

吸收边界就是在原模型的边界处向外延伸15 mm的区域施加瑞利阻尼。等效三维粘弹性边界属于在有限元模型边界沿法线方向延伸5 mm的一层界面单元，即添加粘性阻尼，其处于模型最外围。两者共同组成混合人工吸收边界单元，其平面示意图如图4所示。

图4 混合人工吸收边界的铝板模型

图4给出了含吸收边界模型的示意图，与初始模型相比，除了添加了混合人工吸收边界单元，其他仿真参数，包括模型尺寸、激励信号与激励点、微裂纹模式、接收点等都与初始模型一致，这样可以保证仿真效果的对比度足够清晰。

2.2 仿真结果与分析

2.2.1 初始模型仿真结果

接下来通过将有微裂纹板和无损板的有限元仿真结果进行对比，验证Lamb波与微裂纹相互作用产生二次谐波的非线性效应。

图5(a)和5(b)分别给出了无损板和有损板在9点的的时域接收信号。经过计算，图5(a)中的第一个波包为S0模态直达波，第二个波包为直达S0模态下端面反射波与直达S0模态左端面反射波的混合波。图5(b)有损板的波分布情况与无损板相比，直达S0波后面多了一个新的波包，根据频散曲线数据以及模型的尺寸和波包所出现的时间，可知此新波包为微裂纹反射A0模态波。从图5可以明显看出无损板和有损板的时域接收信号的不同，仿真过程出现的非线性效应主要体现在包含微裂纹信息的新波包内。

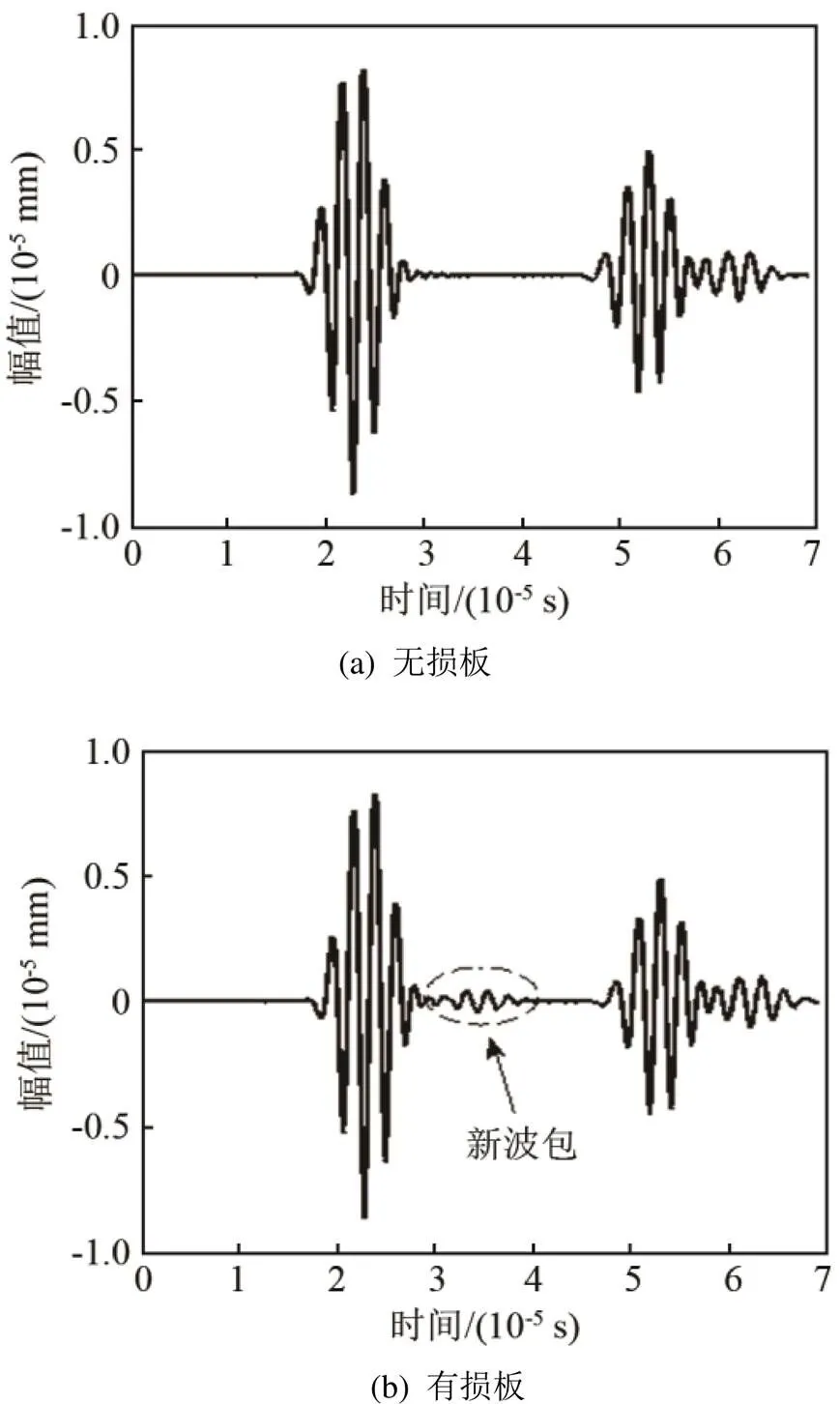
图5 在3D铝板P9点接收的时域信号

2.2.2 吸收边界模型仿真结果

为了确认添加人工混合吸收边界模型的仿真效果，将这两种包含微裂纹模型的时域响应信号进行对比，结果如图6所示。由图6可以明显看出波包的幅值变化，基波和新波包的幅值几乎不变，而吸收边界模型的反射波包幅值出现大幅度下降。这说明Lamb波在板中传播到达边界处后，人工混合吸收边界的存在使反射波的大部分能量被吸收，从而降低了反射波对谐波检测的影响，提高了检测效率。

图6 初始模型和吸收边界模型叠加的时域信号

尽管从时域波形上看，只有反射波的幅值大幅度减小，但是基频信号特别是新波包的频散程度在一定程度上有所降低。图7给出了两种模型的时域接收信号经过短时傅里叶变换后的时频图，除了反射波的能量变化异常明显外，还可以清晰地看出基频信号的能量变得更加集中，而且新波包也明显地从基波中分离了出来，和初始模型相比更容易被观察到，提高了检测精度。

《会稽志》嵊县条下又记：“丹池山在县东七十二里。旧桐柏山，唐天宝六载改为丹池。……南岳真人云：‘越有桐柏、金庭，与四明、天台相连，神仙之宫也。’《真诰》曰：‘桐柏山，高一万五千丈，周回八百里，四面视之如一。其一头在会稽东海际，其一头入海中，是金庭不死之乡……树则苏纡珠碧，泉则石髓金精。其山台尽五色金也。经丹水而行，有洞天从中过，在剡、临海二县之境。”[2]1828

2.2.3 幅值比分析

为了进一步研究Lamb波与裂纹的非线性相互作用关系，先要对Lamb波与微裂纹相互作用产生的新波包进行分析。通过FFT对有损板中的新波包进行频谱分析，结果如图8所示。已知激励源信号的频率为450 kHz，图中第一个波包的峰值对应的频率分量为450 kHz，而第二个波的峰值对应的频率分量为900 kHz。所以，在新波包的频谱中除了出现了基频分量，还出现了二倍频分量，这证实了Lamb波信号与埋藏微裂纹相互作用引发了CAN效应，从而在裂纹反射模态中出现了高次谐波分量。

为了验证微裂纹方向与二次谐波的关系，针对不同方向埋藏微裂纹的Lamb波进行了非线性仿真。保持裂纹的尺寸(长为2 mm，高为1.2 mm)和位置(激励点轴负方向80 mm处)不变，以之前仿真的裂纹方向0°(高度方向垂直模型平面，长度方向为轴方向)为基准，逆时针改变裂纹长度方向的角度，分别取30°、60°、90°、120°、150°进行仿真分析。定义散射系数为时域信号包络中包含裂纹信息的新波包峰值与基波峰值之比[13]。图9给出了不同裂纹角度的接收信号散射系数分布情况。

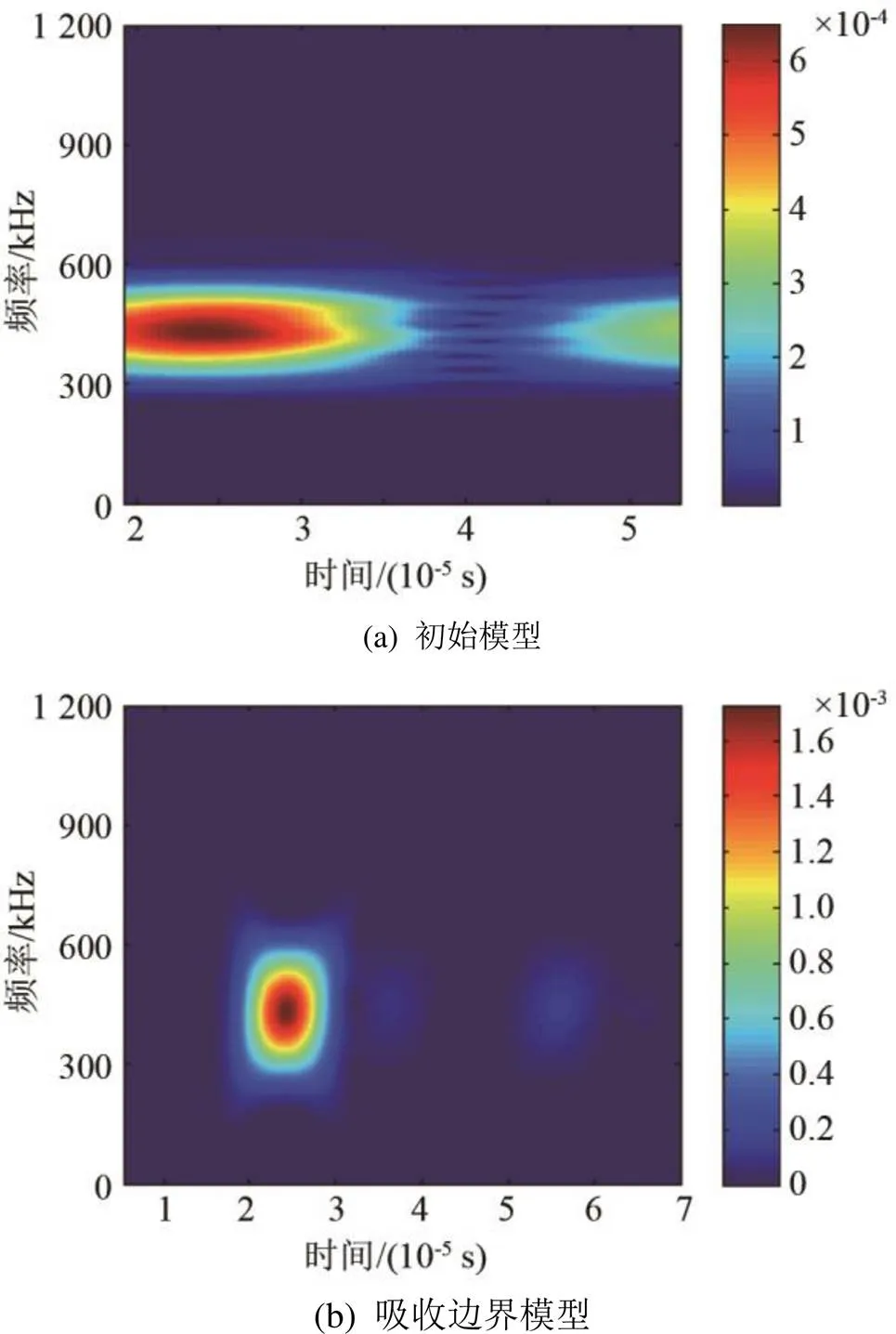
图7 两种模型接收信号的时频分布

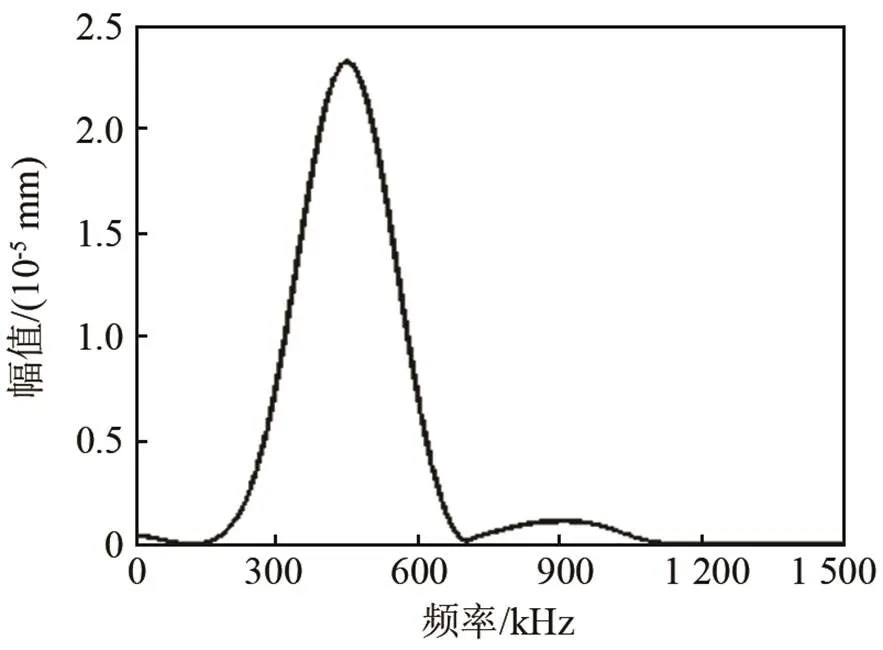
图8 Lamb波与微裂纹相互作用产生的新波包频谱图

图9中不同标记的曲线代表不同的微裂纹方向角度，由图9可知，各个接收点的散射系数一直在变化。由于裂纹的阻挡，6无法直接接收直达波信号，越靠近6接收点，接收到的信号能量越低，其散射系数就越小，同时接收点3和9附近的散射系数相对较大，因为此处不仅接收直达波，还接收了经裂纹尖端折射后的波。整个散射系数分布波动较大，变化规律不够明显，下面将进一步进行幅值比指向性的分析。

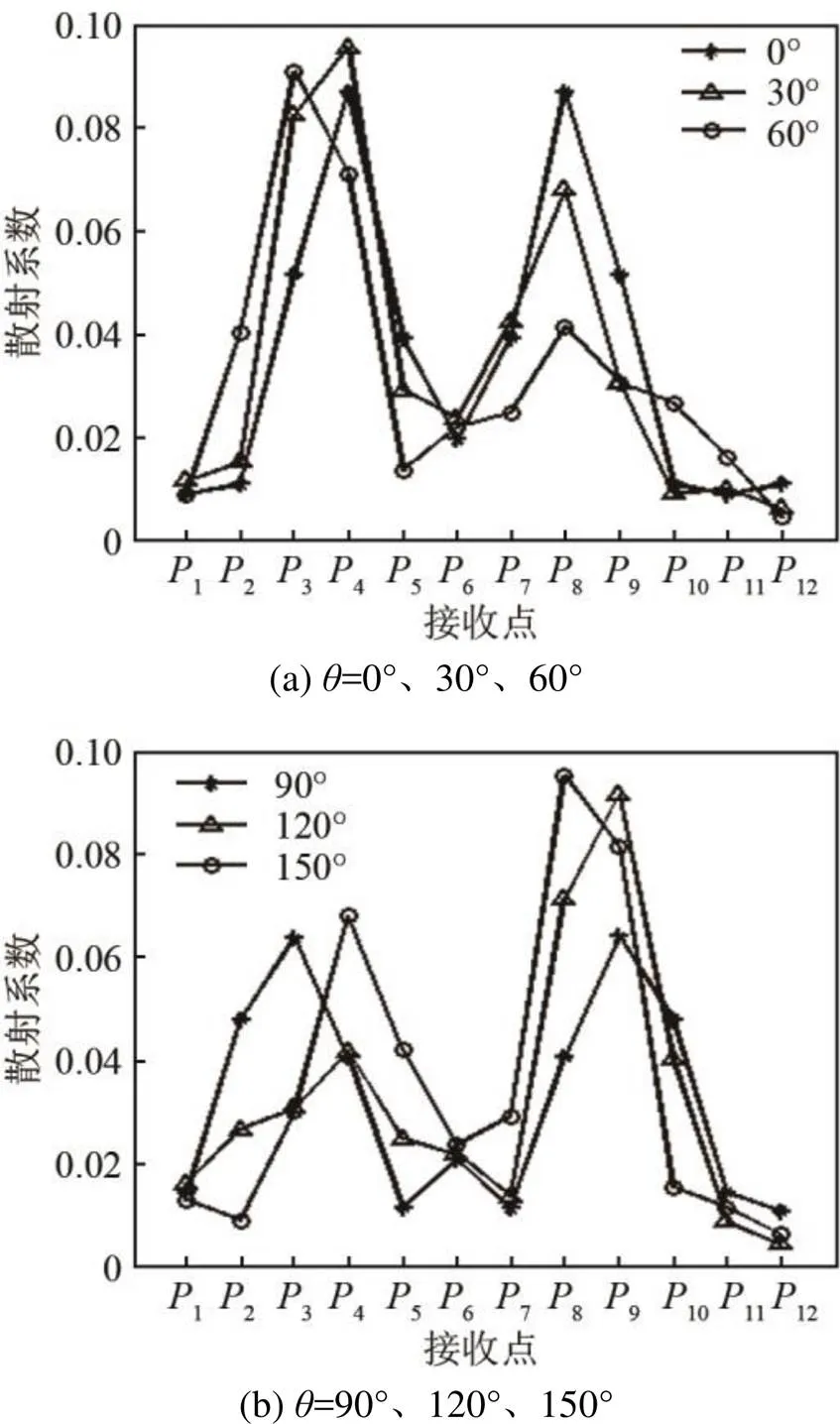
图9 不同裂纹方向角度的接收信号散射系数分布

通过FFT对改变值后仿真得到的裂纹反射A0模态进行频谱分析，可以进一步发现非线性谐波信号与裂纹方向的关系。定义非线性参数幅值比为[2]：

根据式(4)计算初始模型改变裂纹角度后的幅值比，图10给出了所有仿真全部接收点的幅值比指向性图。其中由于1,2,3, ...,12这12个接收点在一个半径为40 mm的圆上，且等间距为30°，正好是时钟的12个整点位，所以图10中的0°到330°既可以表示裂纹的方向角度，也可以与各位置的接收点相对应，即1对应60°，2对应30°，以此类推。

由图10可知，幅值比指向性图在=30°与=150°，=60°与=120°时几乎是关于垂直方向的直线对称的，因此只需要对0°，30°，60°，90°的指向图进行分析。当=0°和90°时，12的幅值比最大，其他接收点的幅值比较小，且本身分布情况几乎关于12和6两点所在直线对称。当=30°和60°时，前向散射的幅值比大于后向散射的幅值比，同时波的传播基本满足广义反射定律，即波经过不同方向裂纹反射后，在反射路径上的对应的接收点幅值比最大。

所以，这种方法对裂纹方向有一定的识别度，但是由于其无法有效地区分=0°或90°的情况而存在一定的局限性。同时其他角度的指向性图幅值比分布波动较大，指向性不够均匀。而含吸收边界的模型仿真在一定程度上弥补了这些不足。

图11给出了增加吸收边界单元后，对不同方向裂纹进行仿真得到的幅值比分布图。由图11可知，=30°、=150°和=60°、=120°时的对称性依然有效，同样只需分析0°～90°的指向图。观察=0°和90°时的幅值比发现了与之前不一样的特征，=0°时，12处幅值比最大，其他接收点的幅值比较小且分布相对均匀，而=90°时，除了12处幅值比大，还有两个幅值比与它相近的接收点，这两个接收点在4和8处，与图9 表现的规律相吻合，这样，就可以有效区分裂纹0°和90°的情况。继续分析=30°和60°时的指向图，发现其规律与未加吸收边界时一样，而且幅值比分布更加均匀，说明吸收边界使二次谐波的能量更加集中了。同时，对两个角度的幅值比分布对比分析后，发现前向散射幅值比虽然大于后向散射幅值比，但是其差值是随着裂纹角度的增加而增加的。由于存在对称性，=120°和150°时的规律与=60°和30°时相同，所以此方法能够较准确地对裂纹方向进行识别。

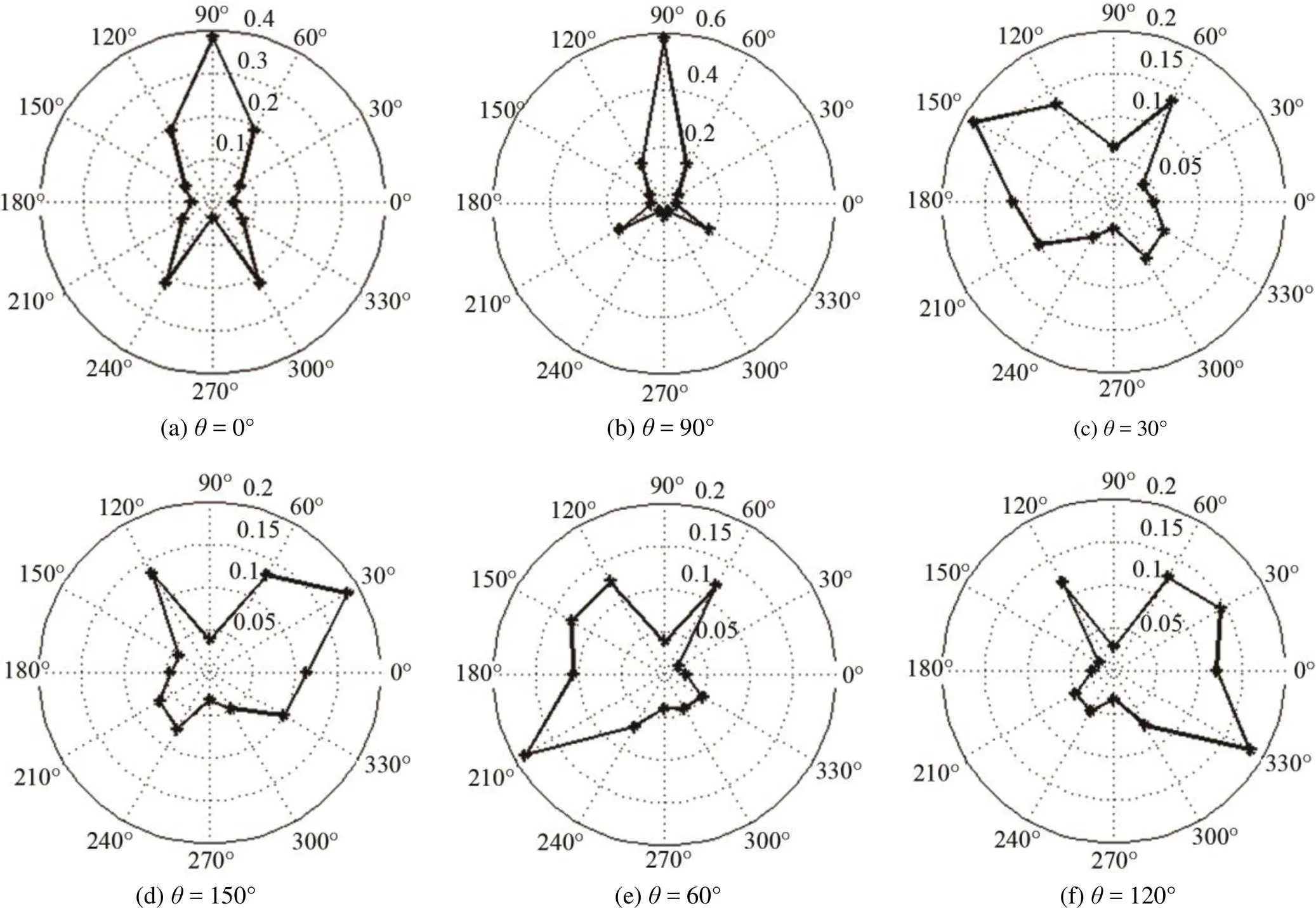
图10 初始模型不同裂纹方向角度(θ)的幅值比(β)的指向性图

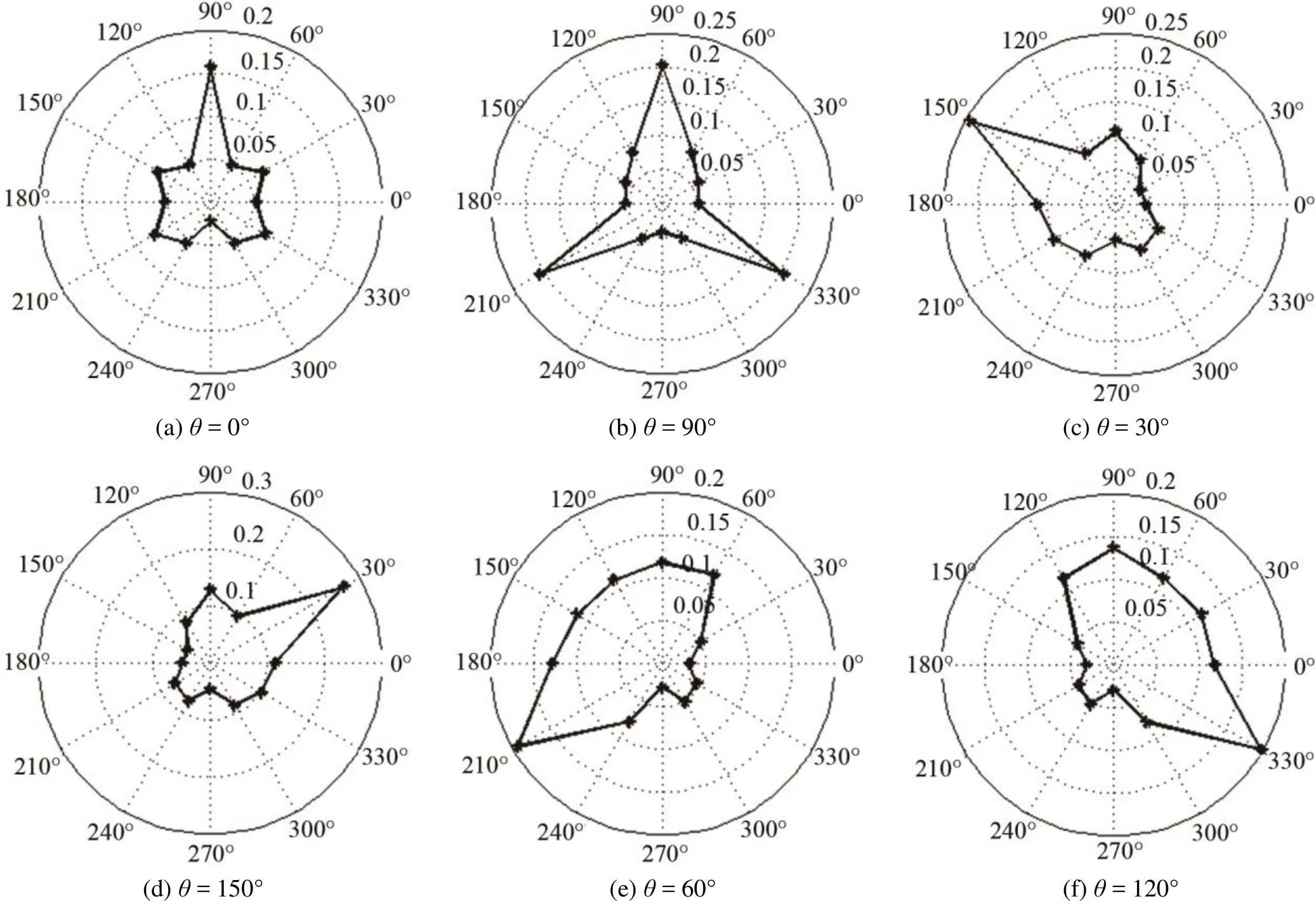
图11 吸收边界模型不同裂纹方向角度(θ)的幅值比(β)的指向性图

3 结论

针对结构中不同裂纹方向的问题，本文建立了一种包含吸收边界的3D有限元铝板模型，分别将不同方向角度的埋藏微裂纹嵌入其中并进行仿真分析。结果表明，随着裂纹方向的变化，Lamb波在板中传播的路径受到非线性效应影响。对产生的二次谐波进行频谱分析后，发现散射区的波分布规律可以一定程度上评估裂纹的方向，而且加入人工吸收边界后，仿真效果得到明显改善。通过确认幅值比最大的接收点和比较信号前向与后向散射区幅值比的分布情况，根据反射定律，可以推测出裂纹的角度指向。因此，此方法可以有效地对裂纹方向进行识别。

[1] KUDELA P, RADZIENSKI M, OSTACHOWICZ W, et al. Structural health monitoring system based on a concept of Lamb wave focusing by the piezoelectric array[J]. Mech. Syst. & Signal Pr, 2018, 108: 21-32.

[2] ZHAO Y, LI F, CAO P, et al. Generation mechanism of nonlinear ultrasonic Lamb waves in thin plates with randomly distributed micro-cracks[J]. Ultrasonics, 2017, 79: 60-67.

[3] YANG R, HE Y, ZHANG H. Progress and trends in nondestructive testing and evaluation for wind turbine composite blade[J]. Renew. & Sust. Energ. Rev, 2016, 60: 1225-1250.

[4] CASAVOLA C, PALANO F, DE F C, et al. Analysis of CFRP joints by means of t-pull mechanical test and ultrasonic defects detection[J]. Materials, 2018, 11(4): 620-636.

[5] LIU X, BO L, YANG K, et al. Locating and imaging contact delamination based on chaotic detection of nonlinear Lamb waves[J]. Mech. Syst. & Signal Pr, 2018, 109: 58-73.

[6] METYA A K, TARAFDER S, BALASUBRAMANIAM K. Nonlinear lamb wave mixing for assessing localized deformation during creep[J]. Ndt & E Int, 2018, 98: 89-94.

[7] LI W, CHO Y, ACHENBACH J D. Detection of thermal fatigue in composites by second harmonic Lamb waves[J]. Smart Mater. & Struct, 2012, 21(8): 085019.

[8] JIAO J, SUN J, LI N, et al. Micro-crack detection using a collinear wave mixing technique[J]. Ndt & E Int, 2014, 62(2): 122-129.

[9] JIAO J, MENG X, HE C, et al. Nonlinear Lamb wave-mixing technique for micro-crack detection in plates[J]. Ndt & E Int, 2017, 85: 63-71.

[10] ZHOU C, HONG M, SU Z, et al. Evaluation of fatigue cracks using nonlinearities of acousto-ultrasonic waves acquired by an active sensor network[J]. Smart Mater. & Struct, 2013, 22(1): 015018.

[11] WANG Y, GUAN R, LU Y. Nonlinear Lamb waves for fatigue damage identification in FRP-reinforced steel plates[J]. Ultrasonics, 2017, 80: 87-95.

[12] YELVE N P, MITRA M, MUJUMDAR P M. Detection of delamination in composite laminates using Lamb wave based nonlinear method[J]. Compos. Struct, 2017, 159: 257-266.

[13] LU Y, YE L, SU Z, et al. Quantitative evaluation of crack orientation in aluminium plates based on Lamb waves[J]. Smart Mater. & Struct, 2007, 16(5): 1907-1914.

[14] 焦敬品, 李海平, 吕洪涛, 等. 超声波与不同方向微裂纹的非线性相互作用数值仿真[J]. 北京工业大学学报, 2018, 44(5): 708-715.

JIAO Jingpin, LI Haiping, LYU Hongtao, et al. Numerical simulation of nonlinear interaction between ultrasonic and micro-cracks in different directions[J]. Journal of Beijing University of Technology, 2018, 44(5): 708-715.

[15] WANG W, BAO Y, ZHOU W, et al. Sparse representation for Lamb-wave-based damage detection using a dictionary algorithm[J]. Ultrasonics, 2018, 87: 48-58.

[16] 杨晓华, 刘学君, 马广婷. 基于多频率数据融合的Lamb波损伤定位研究[J]. 声学技术, 2017, 36(2): 133-139.

YANG Xiaohua, LIU Xuejun, MA Guangting. Research on multi-frequency data fusion based Lamb wave damage localization[J]. Technical Acoustics, 2017, 36(2): 133-139.

[17] YELVE N P, MITRA M, MUJUMDAR P M. Spectral damage index for estimation of breathing crack depth in an aluminum plate using nonlinear Lamb wave[J]. Struct. Control & Hlth, 2014, 21(5): 833-846.

[18] RADECKI R, SU Z, CHENG L, et al. Modelling nonlinearity of guided ultrasonic waves in fatigued materials using a nonlinear local interaction simulation approach and a spring model[J]. Ultrasonics, 2018, 84: 272-289.

[19] DIXON S, EDWARDS R S, JIAN X. Inspection of rail track head surfaces using electromagnetic acoustic transducers (EMATs)[J]. Insight, 2004, 46(6): 326-330.

[20] 谷音, 刘晶波, 杜义欣. 三维一致粘弹性人工边界及等效粘弹性边界单元[J]. 工程力学, 2007, 24(12): 31-37.

GU Yin, LIU Jingbo, Du Yixin. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element[J]. Engineering Mechanics, 2007, 24(12): 31-37.

Research on the application of nonlinear Lamb wave to identifying the directions of micro-cracks in three-dimensional aluminum plate

ZHU Weiguang, GUAN Liqiang, LI Yifeng

(College of Computer Science and Technology, Nanjing Tech University, Nanjing 211800, Jiangsu, China)

Crack direction recognition is an important part of structural quality monitoring. To solve the problem of detecting different directions of the micro-cracks buried in three-dimensional thin plate structures, a method of numerical simulation is adopted. An improved three-dimensional aluminum plate model including artificial viscoelastic absorbing boundary is established by finite element software ABAQUS. The nonlinear interaction between the S0 mode Lamb wave and the buried micro-crack is investigated. The buried micro-crack is embedded at a fixed position in the plate model. Different micro-crack directions under the same excitation condition are simulated. Fourier frequency spectral analysis is applied to the received signals. Then, the directivity diagrams of the amplitude-ratio of second harmonic to fundamental wave in different crack directions are compared and discussed. Simulation results indicate that cracks in different directions have a distinct effect on the distribution of Lamb wave scattering field in the crack zone; The wave propagation path satisfies the reflection law, and the amplitude ratio of forward-scattering signal is generally larger than that of the back-scattering signal; The artificial absorption boundary can minimize the influence of the reflected wave, and the energies of the fundamental frequency and second harmonic signals become more concentrated and stable; Meanwhile, the amplitude ratio difference between forward-scattering and back-scattering increases with the increase of crack direction angle. The detection results show that the method can identify any crack direction angle within the allowable error range.

nonlinear Lamb wave; three-dimensional buried crack; micro-crack direction; absorbing boundary; amplitude ratio

TB559

A

1000-3630(2020)-02-0161-08

10.16300/j.cnki.1000-3630.2020.02.007

2019-03-10;

2019-04-22

国家自然科学基金(615741222)资助项目、江苏省六大人才高峰高层次人才项目

祝伟光(1992－), 男, 江苏东台人, 硕士研究生, 研究方向为Lamb波无损检测。

李义丰,E-mail: lyffz4637@163.com