基于模糊PI的管道清淤机器人控制系统研究

罗继曼，戴璐璐，印 辉，刘泽明，刘士恒

(沈阳建筑大学机械工程学院，辽宁 沈阳 110168)

0 引言

目前，很多高校和公司正致力于管道机器人的研发并取得了可观的成就，而可以进行自主清除淤泥工作的机器人还很少，清淤机器人控制系统设计还不完善。江苏工业学院研究并开发了一种缆控清淤机器人，该清淤机器人的控制系统核心为51单片机。上海交通大学对管道检测机器人控制和导航系统进行了详细的研究，实现了管道机器人自主路径规划、导航和动作的智能控制[1-3]。上述文献中所涉及的清淤机器人均只具备检查管道内部破损情况以及代替工作人员进行穿缆作业的功能，自主清淤能力较差，所以对清淤机器人控制系统的研发工作仍然需要进一步深入，提高清淤机器人的自动化水平。

本文根据该机器人的结构特点和功能要求进行了整机控制系统的设计，以增强该机器人的可控性，实现自主清淤。为了确保该机器人能够平稳、可靠地运动，需要对轮式机构协调运动控制策略进行深入研究，其中包括提高单组行走单元控制性能的控制算法和增强多电机系统同步性能的协调控制策略。

1 机器人的结构和硬件配置

1.1 管道清淤机器人机械系统结构

清淤机器人的结构如图1所示，其机械本体主要由3个部分组成，分别为轮式行走机构、步进机构和清淤机构。

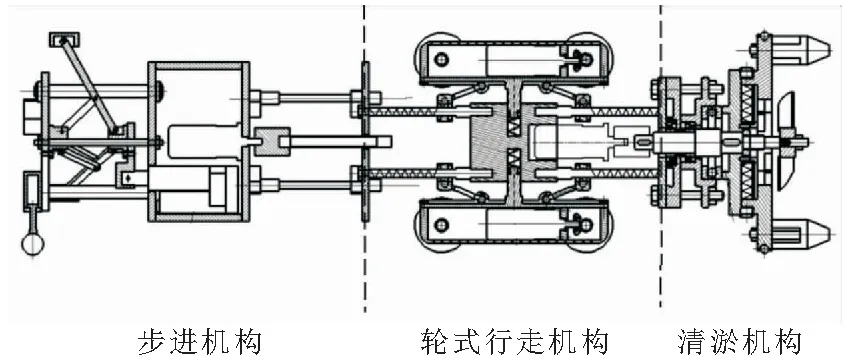
图1 新型管道清淤机器人总体结构

由图1可知，轮式行走机构处于整机的中间位置，是机器人前进的主要驱动机构。轮式行走机构结构如图2所示，该机构主要由均布在圆周内3组行走单元组成，各由1个电机驱动。该机器人采用全驱动的方式，在理想状态下，3个独立的驱动电机速度应保持一致，所以该控制系统需要有较好的调速能力，使机器人能够平稳、可靠地运动。

图2 轮式行走机构

步进推动机构是管道清淤机器人前进的辅助机构，结构如图3所示。当轮式行走机构中的行走单元的3组轮都处于打滑状态时，步进推动机构启动辅助清淤机器人前进。

清淤机构通过内置电机1带动主轴旋转实现清淤头的转动，从而刮削下管道内壁的淤泥，是机器人完成清淤作业的主要执行机构，其结构如图4所示。

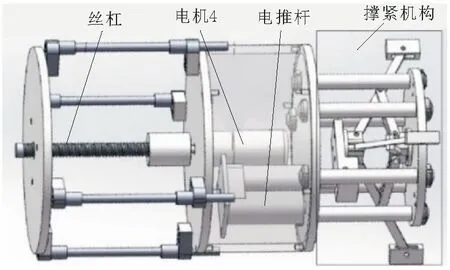
图3 步进机构

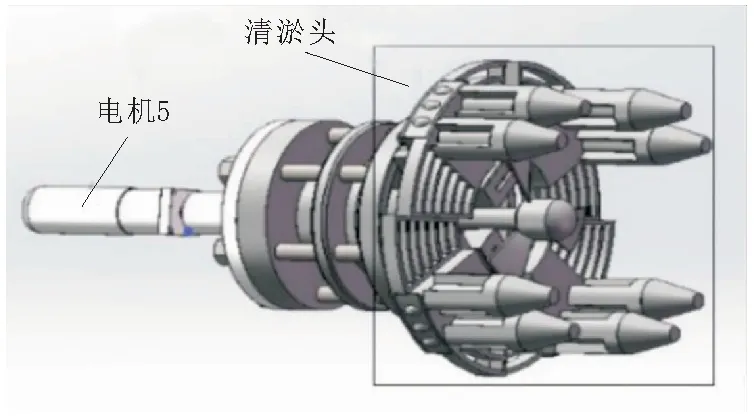
图4 清淤机构

1.2 控制系统硬件配置

根据设计的目的和要求，给出了如图5所示的系统框图。本机器人控制系统可按功能划分为上位机和微控制器STM32。输入模块由压力检测模块、测速模块、光电模块组成；输出模块由电机驱动模块、驱动电机、电推杆组成；通讯模块是Wi-Fi模块。STM32单片机作为系统的核心控制器件负责对各电机的精确控制、上位机的命令识别及数据的传输[4-5]。电机驱动模块将控制器产生的小信号放大[6]，并根据微处理器输出的PWM信号控制直流电机的速度和方向。编码器负责实时测量直流电机的速度和方向，便于对驱动电机进行闭环控制。

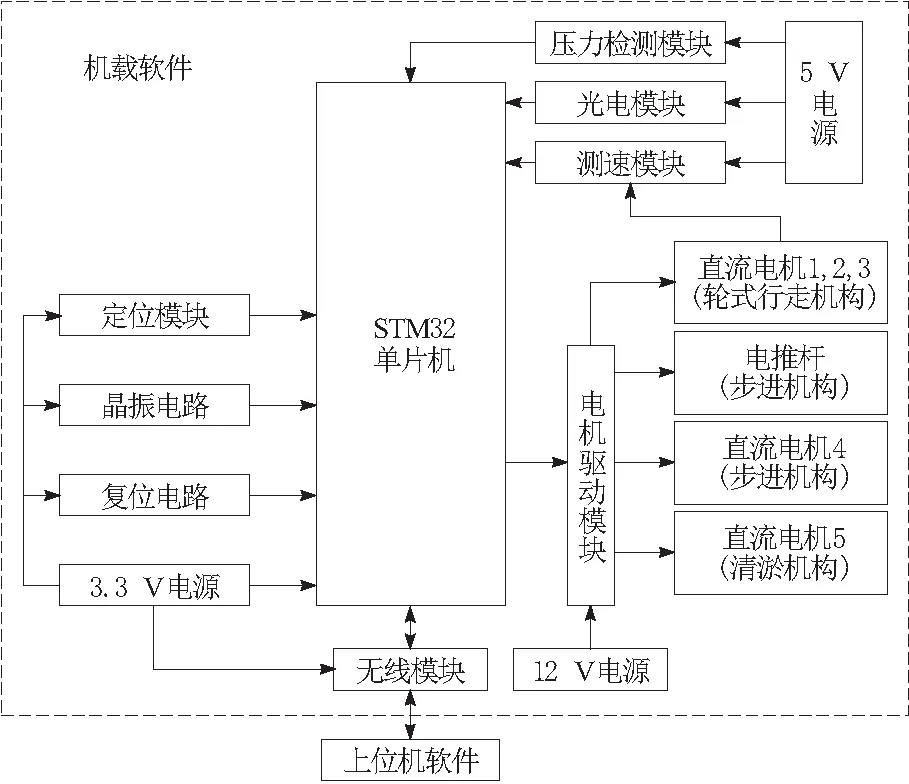
图5 系统框图

2 行走单元控制系统的研究与仿真

清淤机器人驱动系统是机器人顺利完成作业的核心，是清淤机器人具有良好的通过性和越障能力的保障。在理想状态下，3个独立的行走单元的运动应具有同步性。但如果每组行走单元对于转速的跟随能力不强，使转速跟踪误差较大时，单组行走单元的控制性能不能达到要求，那么轮式驱动系统的同步协调性能也不能够得到保证。因此必须采用适当的控制算法来提高行走单元的控制精度及抗干扰性。

为了满足运行中电机控制需要达到一个较高精度的要求，本文的行走单元驱动系统采用广泛使用的双闭环调速方法[7]，如图6所示。从行走单元控制系统的反馈结构上看，以电流为内环反馈，转速为外环反馈。考虑到转速环调节是能确保该调速系统具有良好的跟随性和抗干扰性的根本因素。故电流环的调节器采用传统的PID控制算法，而转速环调节器采用模糊PID控制算法，以提高系统的自适应性与鲁棒性,实现电机无静差稳态调节[8]。

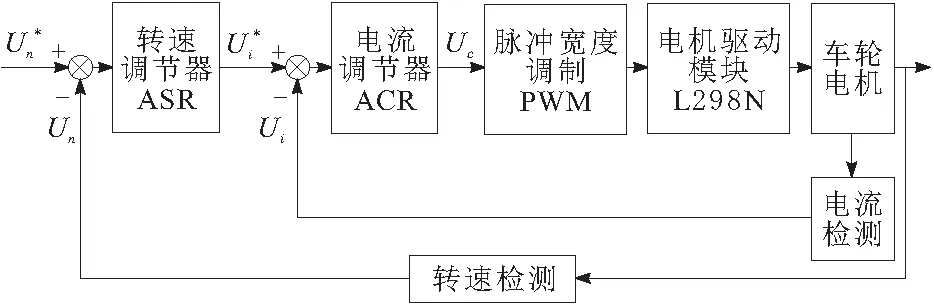
图6 双闭环控制系统

2.1 传统PID控制算法

在行走单元控制系统中，电流环控制器采用了传统的PID控制算法，该算法以其高稳定性，原理简单等特点广泛应用在直流电机的控制系统中，PID控制原理如图7所示。

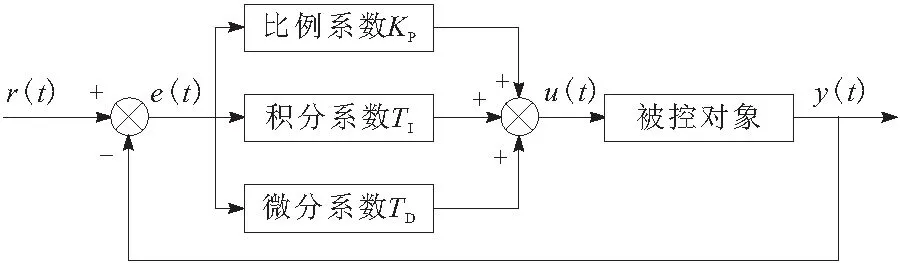
图7 PID控制原理

在实际应用中，可根据系统需要灵活地进行比例、积分、微分环节的组合。微分调节器对输入信号的噪声很敏感，令控制系统容易受到高频电磁的干扰，降低系统的抗干扰性能。由于管道环境较复杂，行走单元驱动电机工作时所需转速及承受的负载随时可能变化。例如，为了提升清淤效率，机器人需要根据淤积量匹配不同的转速。同时机器人承受的阻力产生变化，反映到电机上即为电机负载变化[9]。因此为了避免降低电机控制系统的抗干扰性，本次设计控制系统调节器采用的是PI控制。

2.2 自适应模糊PI控制算法

PID控制一直用不变的参数控制系统的整个过程,当电机所受负载或速度波动较大时，可能导致原来的参数不再适应变化后的电机控制系统。因此，想要从根本上提高控制系统的动态性能以及控制精度，就要求PID控制器具有很好的时变性，能根据控制系统的变化而变化。模糊PID控制直接采用语言控制规则，可完全不依赖于被控对象的精确数学模型，通过用模糊控制理论规则针对PID控制器实时在线自动对其参数进行整定。它在电机控制系统应用中具有控制精度强和鲁棒性好等优点[10]，对外界的干扰也具有很强的抑制能力[11]。

转速环模糊PI控制器原理如图8所示，直流电机模糊PI参数的整定为[12]：

KP=KP0+ΔKP

(1)

KI=KI0+ΔKI

(2)

ΔKP和ΔKI为模糊控制器输出的修正值；KP0和KI0为PI控制器参数的原始值。

图8 模糊PI控制器

2.3 行走单元控制系统的仿真

本文利用Simulink软件对行走单元的驱动系统进行建模和仿真。

转速环采用模糊PI控制器，其中模糊化系数Ke=10，Kec=3.42；解模糊化系数K1=0.8，K2=48；PI控制器初始系数KP0=25，KI0=8。

电流环采用的是传统PI控制器，为了防止电流过大，设置了限幅环节。经过反复调节，确定PI控制器参数KP1=14.8且KI1=5。轮式机构驱动电机的额定电流为13 A,因此电流环限幅[-18,18]。

2.4 仿真结果对比及分析

本文所设计的双闭环控制系统中，转速环是增强系统对负载变化能力抗干扰能力的主要控制环节，因此对转速环控制器分别采用传统PI和模糊PI算法进行仿真实验对比。

2.4.1 行走单元调速仿真

设定行走单元的起始速度为180 r/min；在2.5 s时，调整行走单元设定转速为150 r/min，行走单元的转速仿真结果对比如图9所示。

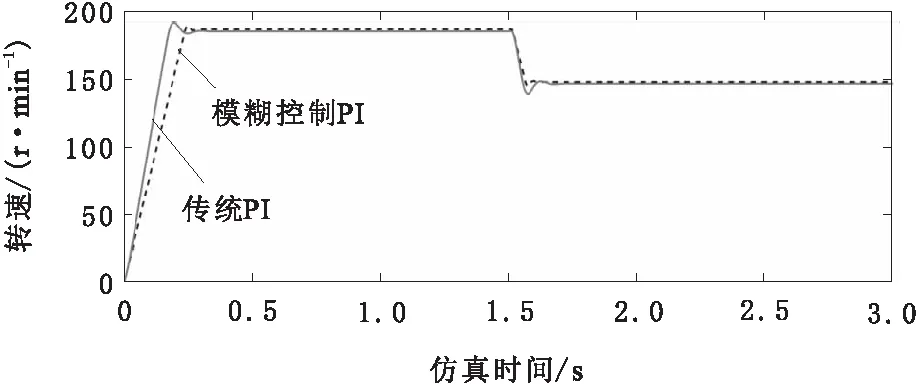
图9 转速仿真结果

由图9可知，2种控制方法都能令转速很快地达到指定值。但基于模糊PI控制的系统，在电机启动时，转速超调量更小，稳定性较好；进行减速控制时，响应速度较快，经过少量跌落后稳定在给定速度。

2.4.2 负载扰动仿真

行走单元给定转速设为180 r/min，把负载改为扰动负载。行走单元的初始负载转矩4 N·m；在1.5 s后负载变为6 N·m，电机转速仿真结果对比如图10所示。

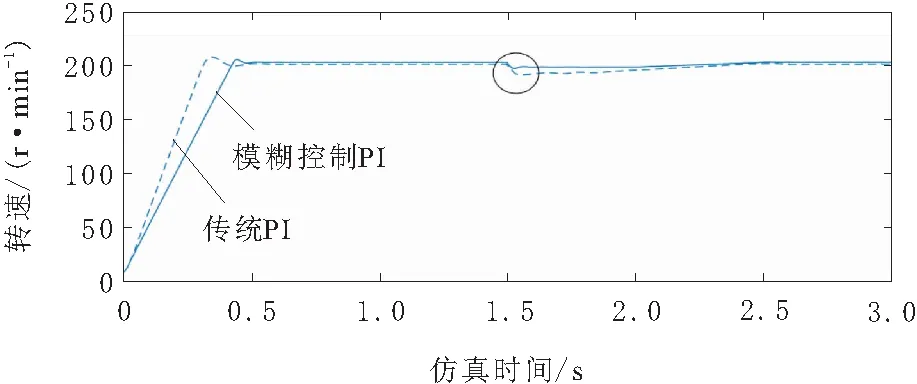
图10 转速仿真结果

由图10可知，在加上负载扰动的情况下，转速有所下降，经过系统自动调节，使得转速重新恢复为指定值。但模糊控制PI拥有更小的转速下降量，并且恢复至指定转速值的速度更快。

这说明模糊PI控制系统具有更好的稳定性、抗干扰力更强，有效提高了清淤机器人的控制灵敏性。

3 轮式行走机构的3组行走单元的同步控制研究与仿真

为了进一步提高该机器人运动的平稳性，增强3组行走单元的同步协调性，本文在该机器人行走单元各自控制系统的基础上，通过速度补偿器，建立3组行走单元运行时速度的关联性，以保证行走单元运动特性的同步控制。

3.1 偏差耦合器设计

本文采用基于偏差耦合的控制策略实现3组行走单元的同步控制，对每一组行走单元而言，都要考虑自身的转速跟踪误差和与其余行走单元的转速同步误差[13]。要使各行走单元同步运行，应使它们的跟踪误差和同步误差稳定收敛，即满足：

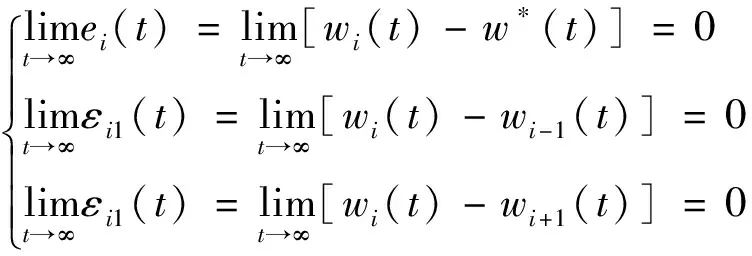
(3)

行走单元偏差耦合控制系统的结构如图11所示，它主要由3个部分组成：系统的混合模块(MUX)、每组行走单元对应的分离模块(DEMUX)和速度补偿器模块。其中最重要的组成部分是速度补偿器模块，由它提供每组行走单元的补偿信号[14]。由于该结构将系统的各行走单元耦合起来，形成一个闭环结构，因此当任意一组行走单元受到干扰时，其他行走单元都能实时、准确地调整速度，从而达到较高的同步性能。

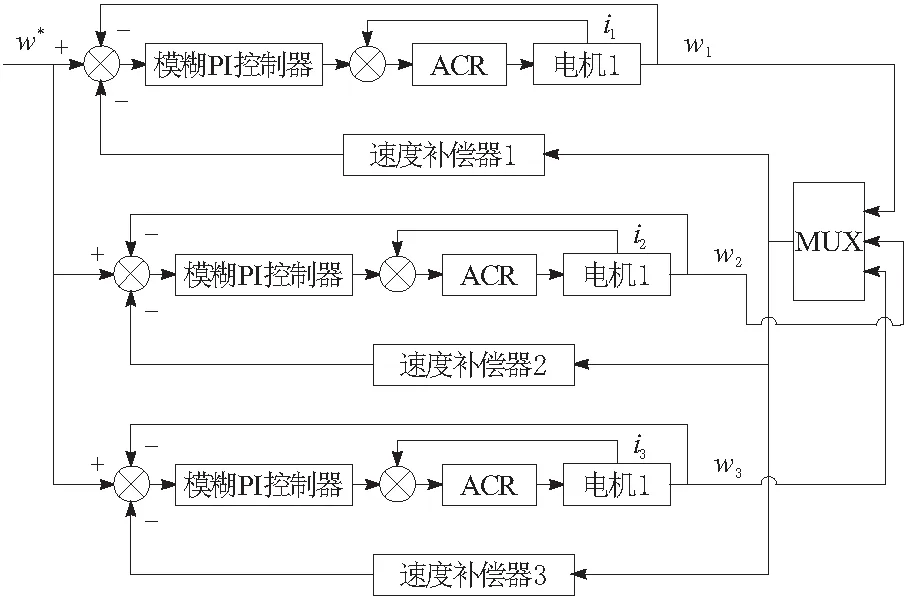
图11 偏差耦合控制系统

速度补偿器1的内部结构如图12所示，在该模块中将行走单元1的反馈速度值与其他行走单元的反馈值做差，并分别乘以各自的耦合系数Kir，再将所有的结果相加后作为速度信号。

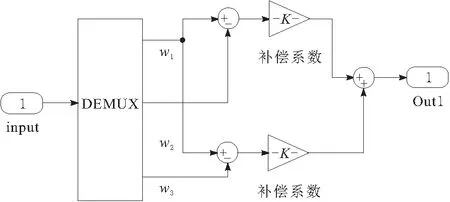
图12 速度补偿器1

速度耦合系数Kir所起到的作用是当任意行走单元驱动电机受到外界环境的扰动，例如负载突然增加或者减少，受到冲击载荷等，减小电机间的同步偏差，并且不会增加系统的超调，从而避免了输出转矩的抖动。Kir的取值与电机的转动惯量有关，计算公式为

Kir=Ji/Jrr=1，2

(4)

Ji为系统中第i台电机的转动惯量；Jr为电机i相邻的第r台电机的转动惯量。则电机1的速度补偿值e1=K11(w1-w2)+K12(w1-w3)。同理可得其他电机的速度补偿值。

3.2 仿真结果分析

利用 MATLAB 中的 Simulink平台对3组行走单元的同步控制进行仿真，其中各行走单元转速均采用基于模糊PI控制的双闭环控制系统，通过速度补偿器，建立3组行走单元之间的耦合关系，以保证它们的同步协调运转。

3.2.1 调速仿真

设定3组行走单元的起始速度均为180 r/min；在2 s时，调整电机设定转速为150 r/min；在4 s时，调整电机设定转速为100 r/min，电机转速仿真结果如图13所示。

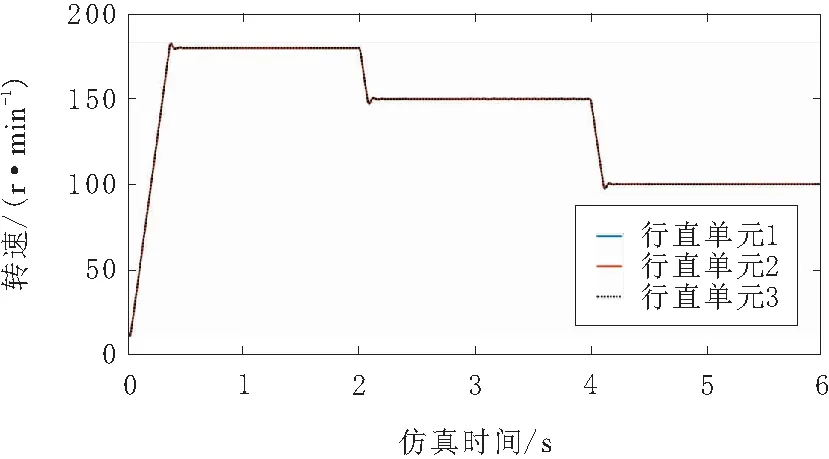
图13 转速仿真结果

由图13可知，3组行走单元的同步性较好，电机起动时出现了轻微超调，但很快稳定在给定转速180 r/min上。当给定转速变化时，3台电机的转速同步变化，速度产生轻微波动最终稳定在变化后的给定转速量。

3.2.2 负载扰动仿真

设定行走单元给定速度为180 r/min，给定负载转矩为4 N·m；在1.5 s时，给行走单元1加负载扰动；在4 s时，给3组行走单元同时添加负载扰动。电机转速仿真结果如图14所示。

电机系统稳态运行时，系统可以按照给定速度完成3组行走单元同步运行。在1.5 s时，仅行走单元1收到负载扰动，行走单元1转速首先产生微量下降，由于行走单元转速之间有耦合关系，行走单元2和行走单元3转速很快跟随变化。在4 s时，当3组行走单元同时受到负载扰动时，其转速同时产生少量速度波动，并快速恢复至指令速度。

图14 转速仿真结果

因此当系统中一旦有电机出现扰动，由于耦合控制器的作用，就会使其他电机产生同步控制反应，相互传递扰动信号，使得整个系统都对扰动做出相应的反馈，进而消除扰动，可有效增强3组行走单元的协调控制性能，保证机器人在管道内平稳灵活地行驶。

4 实验

在本次实验中，主要按照以下3个步骤进行：整机功能测试、行走单元测试和轮式行走机构的同步测试。

4.1 整机功能测试

为了检验控制系统的稳定性和机器人各个功能模块是否正常工作，先进行整机功能测试，查看机器人在水平管道内和15°坡度的管道内运行情况,如图15和图16所示。

图15 水平管道内机器人运行情况

图16 有坡度的管道内机器人运行情况

经测试，该机器人在水平管道内运动时各功能均按设计实现，且运动平稳；在管道内可沿直线行驶，无偏移现象，满足设计要求；在启动和停止时，没有明显抖动，说明该控制系统有效可靠。

4.2 轮式驱动机构的行走单元测试

对轮式驱动机构的1组行走单元进行实验，检测转速反馈情况和速度的跟随性。行走单元的行驶速度设为200 r/min，速度采样周期为30 ms，系统在3 s内的电机的速度响应曲线如图17所示。

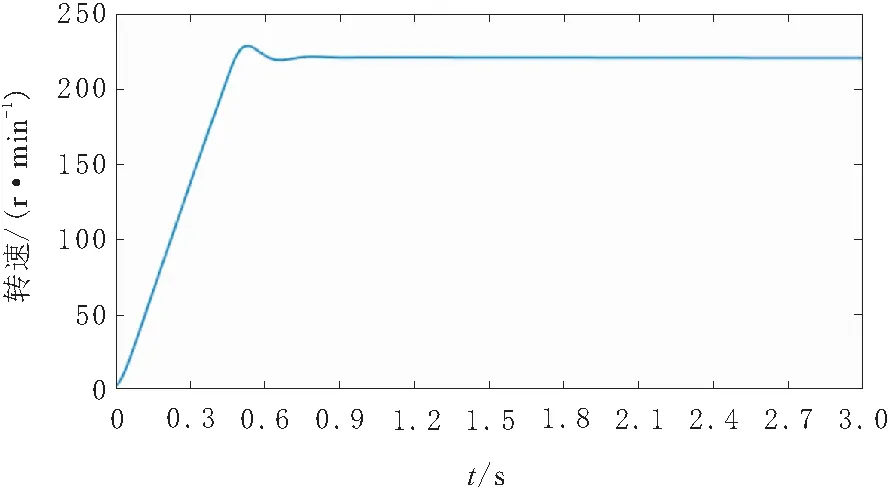
图17 速度响应曲线

由图17可知，系统出现一次震荡后便处于稳定，系统上升时间tr=0.5 s,调节时间ts=0.15 s，稳态误差ess=5%，超调性很小；测量结果表明该系统控制精度高、具有良好稳定性。

4.3 轮式驱动机构3组行走单元同步测试

为了检验轮式行走机构的协调控制效果，仅对轮式驱动机构进行实验，在管道内2个不同位置放置障碍，以检测轮式行走机构3个行走单元的同步性。得到轮式驱动电机速度偏差曲线如图18～图20所示。

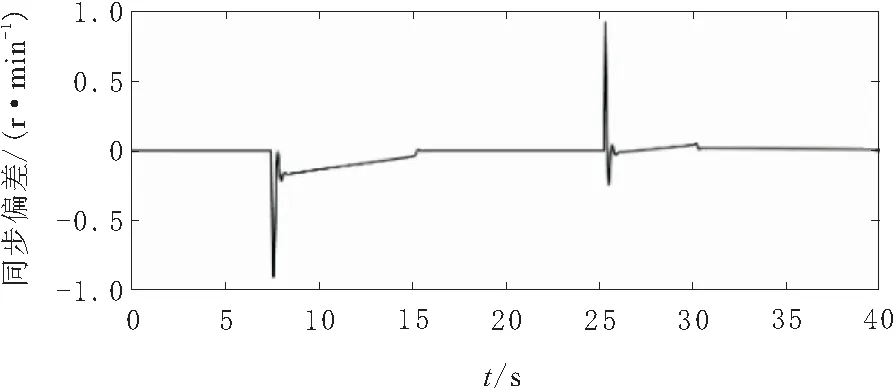
图18 行走单元1与行走单元2速度偏差曲线

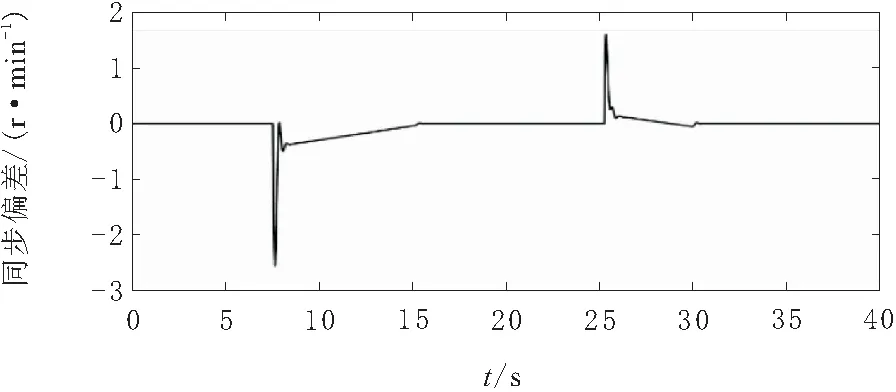
图19 行走单元1与行走单元3速度偏差曲线

从电机的同步速度偏差曲线计算得出，稳态时系统的同步误差几乎为0，当机器人碰到障碍时，最大同步误差为1.5 r/min。说明轮式驱动机构3个行走单元同步性良好，抗干扰性能力强，能够满足系统要求。

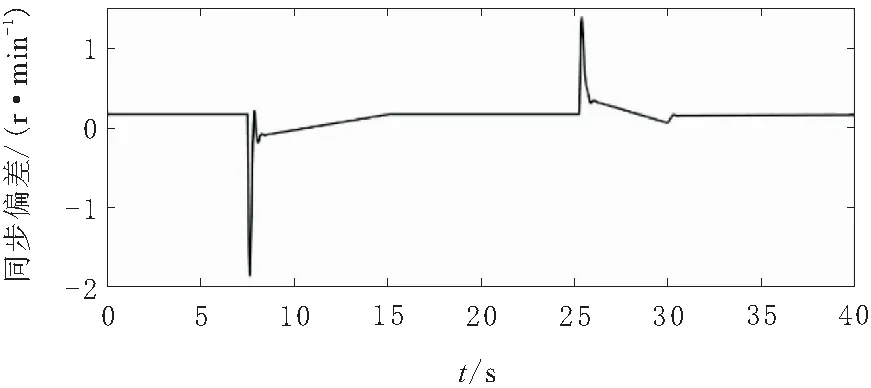
图20 行走单元2与行走单元3速度偏差曲线

5 结束语

根据清淤机器人的行走方式，进行该机器人的整体控制系统设计，并完成了机器人控制系统各模块硬件配置，经实验验证该控制系统可控性强，可实现对机器人在管道内运行的各个动作控制。

对清淤机器人的电机控制算法进行了研究，设计完成了基于模糊PI控制的电机控制系统，并利用Simulink对基于模糊PI控制和传统PI控制的行走单元的转速控制效果进行了比较。仿真结果表明基于模糊PI算法的控制系统速度跟随性更好、系统具有更好的可控性和抗干扰性。可实现对该机器人轮式驱动系统的速度精确控制。

针对清淤机器人的轮式驱动系统，设计了速度补偿器，使3组行走单元的控制系统之间具有耦合关系，以保证3个电机的同步控制。仿真结果表明，在3组行走单元负载有所差异的情况下仍然能够实现同步控制，能够满足清淤机器人运动控制的设计要求。