一度故障模式下推力矢量控制系统定位精度研究

刘春庆，史晨虹，李永宏，李东东，武佳乐

(1.北京精密机电控制设备研究所,北京100076; 2.中冶京诚瑞信长材有限公司,北京100076)

0 引言

推力矢量控制系统是火箭姿态控制系统的执行机构，它通过改变火箭发动机的燃气流排出方向来控制火箭的飞行方向和姿态角[1-2]，是一种典型的位置控制伺服系统。新一代火箭发动机多采用潜入式柔性喷管结构，按照喷管摆动回转中心与喉部的相对位置，潜入式柔性喷管结构可分为前支点柔性喷管和后支点柔性喷管[3]。喷管全轴摆动的驱动装置是2路垂直安装的作动器，与后支点柔性喷管相比，前支点柔性喷管的驱动作动器之间存在明显的运动牵连效应[4]，对喷管俯仰和偏航2个通道的姿态控制和喷管结构可靠性产生不良影响。

针对推力矢量控制精度问题，学者进行了大量卓有成效的研究工作，文献[4]利用三维旋转矩阵理论，计算喷管摆动时驱动作动器的伸长量，并对喷管的牵连效应和控制指令精度进行了研究。文献[5]建立了全轴摆动飞机喷管推力矢量控制系统的动力学模型，并对喷管位置控制系统的定位精度和鲁棒性进行了研究。文献[6]应用空间机构位置分析法、解析几何法、坐标转换法，对某轴对称推力矢量喷管进行运动学分析，建立了完整的喷管驱动机构逆运动学模型。文献[7]针对喷管摆动时作动器牵连运动、正负摆角不对称、力臂变化等因素对摆角控制的影响进行了分析，并研究了负载力矩和伺服机构相关参数对摆动喷管位置控制精度的影响。文献[8]建立了柔性喷管电液伺服机构的动力学模型，并在系统控制中引入模型参考自适应控制器，仿真结果表明系统对自身参数摄动具有良好鲁棒性。

在此，结合工程经验，介绍了前支点柔性喷管位置反解、正解算法求解方案，着重对伺服电机极性反向的一度故障模式下系统的控制算法优化进行分析，获得良好的喷管摆角位置跟踪性能。

1 火箭推力矢量控制系统

本研究前支点柔性喷管的初始输入条件为：作动器上支点坐标A1(418 mm,0 mm,315.6 mm)，B1(0 mm,418 mm,315.6 mm)；作动器下支点坐标A2(457 mm,0 mm,760.5 mm)，B2(0 mm,457 mm,760.5 mm)；作动器零位长度为447 mm。

图1 推力矢量控制系统安装示意

2 推力矢量控制系统位置反解、正解算法分析

推力矢量控制系统的工作原理如图2所示。伺服系统接收控制系统的俯仰和偏航通道姿态角动作指令，通过位置反解控制算法解算为2个通道对应作动器的伸缩量，伺服控制驱动器运行闭环控制算法，通过空间矢量脉宽调制技术，产生伺服电机定子绕组三相全桥功率管开关信号，利用初级电源电能，驱动伺服电机旋转，进而通过减速机构拖动喷管至理想位置。同时，伺服控制驱动器实时采集作动器的位移，通过正解控制算法解算喷管的姿态角，与控制系统指令对比分析，验证喷管位置伺服系统的位置跟踪性能。

图2 推力矢量控制系统工作原理

2.1 位置反解算法分析

所谓喷管位置反解算法，是指已知飞行控制系统输入的俯仰通道姿态角Φ和偏航通道姿态角Ψ，通过位置反解算法，求解驱动喷管运动的双通道作动器的对应位移LA和LB。反解算法通常用作计算作动器线位移闭环控制的指令输入值。

(1)

喷管位置反解算法可通过空间欧拉角旋转[4]进行计算。通过已知的作动器下支点坐标，结合空间旋转矩阵，计算转动俯仰角Φ和偏航角Ψ后的下支点坐标，进而求得作动器实时长度，与作动器初始长度做差即为作动器伸缩量。

俯仰角Φ和偏航角Ψ对应的空间旋转矩阵[4]为

(2)

姿态角空间旋转后的下铰点坐标为

(3)

作动器位移伸缩量为

(4)

|A1A2|和|B1B2|为作动器的初始长度。

2.2 位置正解算法分析

所谓喷管位置正解算法，是指已知作动器的位移MA和MB，通过位置正解算法，求解喷管俯仰角和偏航角。正解算法多用于喷管摆动角度的测量。在本研究推力矢量控制系统中，用于通过作动器的线位移实时采集数据计算喷管的俯仰、偏航通道姿态角。

(5)

正解算法相对复杂，其困难之处在于需要求解式(6)所示的非线性方程组，目前为止，还没有直接的正解方程式，只能采用数值迭代的方法来逼近求解喷管姿态。本研究选择牛顿法进行位置正解算法解算。

(6)

3 推力矢量控制系统位置反解、正解算法的工程实现

推力矢量控制系统位置反解、正解算法牵扯三角函数、矩阵运算及非线性方程运算，不利于飞行控制程序在线执行。因此，飞行控制中通常采用在喷管边界约束条件下，遍寻对应的作动器位移映射值，之后通过多元高阶拟合，得到位置正反解算法的映射多项式，进行位置闭环控制。

位置反解算法对应的拟合算式为

(7)

同理，位置正解算法对应的拟合算式为

(8)

图1所示的前支点柔性喷管，对应式(7)、式(8)的位置反解、正解算法系数如表1所示。

表1 推力矢量控制系统正解、反解算法拟合系数

4 一度故障模式下推力矢量控制系统的控制研究

推力矢量控制系统产品地面齐套测试过程中，发现作动器线位移输出如图3所示。在俯仰通道单向输入指令摆角3.5°正弦信号条件下，作动器运动极性与设计极性相反。通过排查分析，该故障是由伺服电机零位出厂调试过程中，旋转变压器零位电气角度与设计电气零位相差180°造成的，推力矢量控制系统出现所谓的一度故障。

图3 一度故障模式下系统响应曲线

作动器极性故障，若返修伺服电机重新进行旋转变压器调零操作，生产配套周期较长，项目进度节点无法保证。因此，探讨一度故障模式条件下，推力矢量控制系统的位置控制问题具有现实意义。

通过分析推力矢量控制系统的位置正解、反解算法求解方案可知，针对设计极性，存在一组正、反解算法拟合多项式，使作动器按照指令驱动喷管动作，同理，针对极性一度故障情况，仍然可以通过分析求解和曲面拟合等手段，获得满足新极性条件的喷管位置控制算法。

优化完善后，伺服系统的位置反解、位置正解算法拟合多项式系数如表2所示。

表2 优化后系统正解、反解算法拟合系数

5 试验验证

试验测试系统如图4所示，喷管与2个作动器连接，地面测试仪发送系统动作指令，伺服控制驱动器根据指令拖动柔性喷管负载模拟装置动作，地面动力电源作为初级能源为伺服系统提供动力，伺服控制驱动器实时采集作动器相关状态信息，同时利用角位移测量装置采集喷管摆角。

图4 推力矢量控制系统负载测试原理

升级完善伺服控制驱动器软件算法，将优化完善后位置正解、反解算法程序写入数字处理器，开展伺服系统验收测试，俯仰通道单向摆角3.5°条件下系统测试曲线如图5所示，图5中推力矢量控制系统的期望摆角与实际摆角近似重合。将两者的偏差情况整理如图6所示，作动器输出位移与期望值相比最大偏差0.015 mm，较作动器额定行程16 mm占比0.09%；伺服系统输出摆角与期望值相比最大偏差0.007°，较喷管额定摆角3.5°占比0.20%，表明优化完善后伺服系统位置控制精度较高，满足飞行控制系统使用要求。

图5 单向摆角3.5°下系统测试曲线

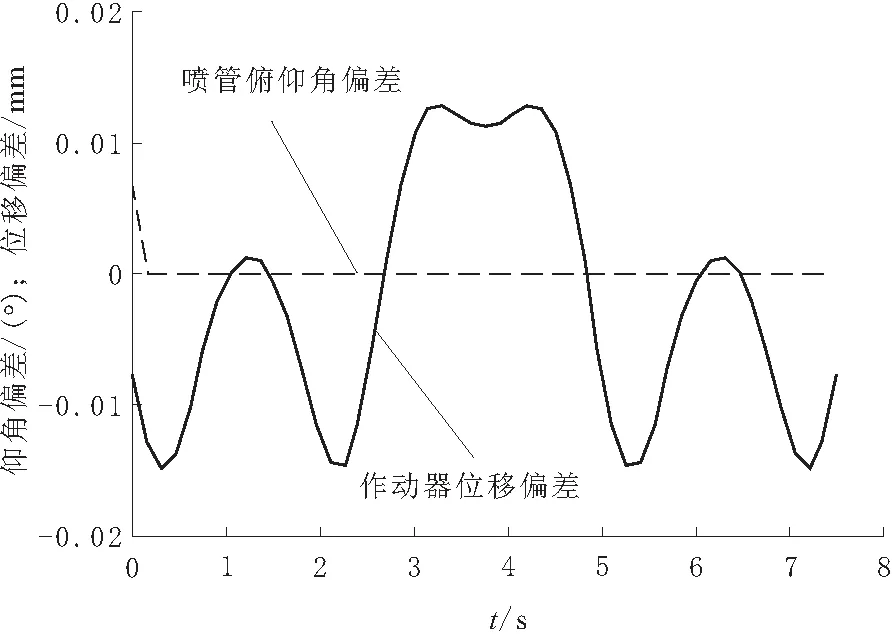
图6 测试结果偏差曲线

6 结束语

通过研究推力矢量控制系统的运动解耦控制问题，介绍了前支点柔性喷管伺服系统的位置反解和位置正解求解方案，并分析推导位置反解、正解算法的工程实现方法。在伺服电机极性反向的一度故障模式下，探讨了系统的算法优化与运动精度控制问题，并通过试验进行了算法验证。

通过以上设计分析与试验验证工作，得出如下结论：

a.对运载火箭前支点柔性喷管推力矢量控制系统而言，系统全轴摆动存在明显的运动牵连耦合效应，可通过运动学反解、正解算法实现喷管俯仰、偏航通道姿态解耦控制。在一定的误差范围内，通常采用二元四阶拟合多项式实现系统的反解、正解算法。

b.伺服电机极性反向条件下，仅通过将飞控系统姿态角指令取反，可以获得期望的作动器位移，但是，受运动学正解算法限制，推力矢量控制系统的输出摆角不能跟踪系统控制指令。

c.上述一度故障模式下，可通过优化完善系统的反解、正解控制算法，解决系统的解耦和精度控制问题，缩短系统研制配套周期。而且，优化算法相比原算法，拟合多项式的偶数项(系数脚标之和为偶数)系数相同，奇数项(系数脚标之和为奇数)系数取反。