基于差分进化算法的手眼标定方法

金 轲，俞桂英，丁 烨，郑建明

(1.上海交通大学机械与动力工程学院，上海 200240；2.浙江万丰科技开发股份有限公司，浙江 嵊州 312400)

0 引言

机器人视觉系统广泛地应用于各种特种机器人中，如飞行机器人[1-3]、轮式机器人[4]和水下机器人[5]等。在复杂的工作环境中，视觉系统能够为机器人提供丰富的环境信息，指导机器人进行正确的决策，完成预定的动作。为了在统一的坐标框架下对视觉系统捕捉的图像数据和机器人工作空间中的三维运动数据进行分析与融合，需要对机器人视觉系统进行手眼标定，以获得视觉传感器坐标系和机器人末端执行器坐标系之间的变换关系。

传统的手眼标定方法[6-8]需要使用已知尺寸的标记物作为参考，分别测定标记物图像数据和机器人末端位姿数据，通过三维空间内的几何约束进行手眼标定求解。Park等[9]提出将手眼标定分为旋转标定和平移标定2个部分，先通过最小二乘法进行旋转标定，再使用旋转标定的结果进行平移标定，但旋转标定的误差会传递到平移标定中。Daniilidis[10]基于对偶四元数理论设计求解算法，通过奇异值分解获取标定结果，实现了旋转部分和平移部分的同时标定，但算法的鲁棒性不强，在噪声的干扰下，计算可能不稳定。Strobl等[11]针对手眼标定优化问题提出了一种基于特殊欧氏群SE(3)的标定误差度量方法，将手眼标定问题转化为一个非线性优化问题，但求解过程中可能落入局部最优，对求解时的初值有较高的要求。Zhao[12]提出了一种基于凸优化的手眼标定方法，将非线性的优化求解问题转化为L∞范数上的凸优化问题进行求解，有效地避免了局部最优问题，但所得的齐次变换矩阵可能不落在特殊欧氏群SE(3)上。Heller等[13]基于多元多项式重新构建了优化目标，并通过迭代进行求解，在考虑了SE(3)约束的同时，保证了所得解的全局最优性，但计算复杂度高。智向阳等[14]提出了一种实现简单的凸优化手眼标定方法，为了解决最优解不满足SE(3)约束的问题，通过QR分解对最优解的旋转矩阵部分进行了正交化，但没有严格地证明正交化后的结果具有全局最优性。

本文针对眼在手机器人视觉系统，提出了一种基于差分进化算法[15]的手眼标定方法。通过李群李代数理论，构建系统手眼标定误差函数。通过差分进化算法对优化问题进行求解，避免了局部最优问题。该方法计算简单，易于实现，在考虑了SE(3)约束的同时，能够保证所得解的全局最优性。

1 手眼标定问题描述

在典型的眼在手机器人视觉系统中，相机固定于机器人末端并随机器人运动。为了统一地分析机器人工作空间中的三维运动数据与图像空间中的图像特征数据，需要通过手眼标定确定相机坐标系到机器人末端坐标系之间的变换矩阵。一般的手眼标定方法需要在世界坐标系中固定一个标定板，如图1所示。将机器人末端执行器移动到不同位置处，采集机器人末端位姿以及对应位置处相机捕捉到的标定板图片，进而计算从相机坐标系{C}到机器人末端坐标系{E}的变换矩阵。

图1 手眼标定示意

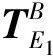
(1)

(2)

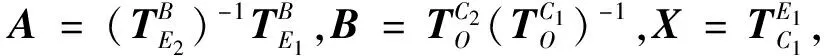
AX=XB

(3)

手眼标定的目的是在已知A和B的条件下求解齐次变换矩阵X。由于实际工程应用中采集到的机器人末端位姿数据和标定板图片数据中存在噪声，求解时使用的齐次变换矩阵A和B并不准确。为了获得较为精确的求解结果，一般采集多组数据进行标定。设标定过程中共采集了n组齐次变换矩阵Ai和Bi(i=1,2，…,n)，选择合适的定义于SE(3)上的误差函数d(·,·)，可将手眼标定过程转化为求解如下优化问题：

(4)

2 基于李群李代数的手眼标定求解

利用位姿变换矩阵的性质，式(3)可改写为

(5)

RA，RB和RX分别为齐次变换矩阵A，B和X对应的旋转矩阵；bA，bB和bX分别为A，B和X对应的平移向量。对式(5)进行推导可得：

RARX=RXRB

(6)

RAbX+bA=RXbB+bX

(7)

式(6)和式(7)分别表示式(3)的旋转部分和平移部分，求解式(3)中的矩阵X等价于求解旋转矩阵RX和平移向量bX。对于采集了多组齐次变换矩阵的手眼标定问题，需要寻求有效的误差函数，以获取最优的RX和bX。

首先考虑通过式(6)获取旋转分量的误差函数，在式(6)中，矩阵RA，RB和RX均为特殊正交群SO(3)上的元素。利用旋转矩阵的性质对式(6)进行推导可得

RA=RXRBRXT

(8)

由于RA和RXRBRXT位于SO(3)中，对其进行对数运算可以获得对应的李代数，结合矩阵对数的性质可以推导得

1n(RA)=RX1n(RB)RXT

(9)

由旋转矩阵的性质可知，1n(RA)和ln(RB)均为反对称矩阵。对任意的三维向量ω，将其对应的反对称矩阵记为[ω]×，代入式(9)可得

[α]×=RX[β]×RXT

(10)

α和β分别为1n(RA)和1n(RB)对应的三维向量。结合反对称矩阵的性质可得

[α]×=[RXβ]×

(11)

对于任意的反对称矩阵，其对应的三维向量是唯一的。因此式(11)可改写为

α=RXβ

(12)

式(11)与式(12)等价，描述了手眼标定求解过程中旋转分量上的约束关系。当使用多组齐次变换矩阵Ai和Bi(i=1,2,…,n)进行手眼标定时，定义手眼标定在旋转分量上的误差函数为

(13)

αi和βi∈R3,分别为齐次变换矩阵Ai和Bi的旋转矩阵所对应的李代数。

对于式(7)所示的手眼标定求解的平移分量，定义手眼标定在平移分量上的误差函数为

(14)

RAi∈SO(3)，表示齐次变换矩阵Ai对应的旋转矩阵；bAi,bBi∈R3，分别表示齐次变换矩阵Ai和Bi对应的平移向量。记γ∈R3为旋转矩阵RX对应的李代数，定义手眼标定问题的决策向量x∈R6为

(15)

定义手眼标定问题对应的目标函数为

f(x)=Er(x)+λEt(x)

(16)

λ为权重系数。则手眼标定问题的数学模型可以表示为

(17)

对于任意的三维向量，在SO(3)上都有唯一的元素与其对应。当计算得到最优解x*时，对应的旋转矩阵RX和平移向量bX也唯一确定。该优化问题的构造形式保证了通过求解式能够获得位于SE(3)上的齐次变换矩阵X，而不需要附加额外的约束条件。

3 差分进化算法

为了求解式(17)所示的优化问题，采用差分进化算法计算最优的齐次变换矩阵X。差分进化算法是一种随机启发式搜索方法，拥有较强的全局搜索能力和鲁棒性，能够避免在搜索最优解的过程中落入局部最优。差分进化算法的基本思想是模拟生物进化规律进行搜索迭代，算法实现包含如下步骤。

a.随机生成初代种群。在6维空间中，设定各个维度的上界和下界，随机产生M个符合约束条件的6维向量xi(i=1,2,…,M)。

b.变异操作。设当前种群处于第t代，对于下一代的变异个体hi(t+1)，其产生的方式为

hi(t+1)=xp1(t)+F(xp2(t)-xp3(t))

(18)

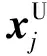
c.交叉操作。对变异个体hi(t+1)进行交叉，生成新的待选个体vi(t+1)，具体的操作为

(19)

vij(t+1)和xij(t)分别为vi(t+1)和xi(t)的第j个分量(j=1,2,…,6);r为区间[0,1]内的随机数;CR∈[0,1]为交叉因子。

d.选择操作。设置算法的评价函数为手眼标定问题的目标函数f(x)，通过评价函数确定差分进化方向，生成第t+1代个体：

(20)

定义第t代种群中对应评价函数值最小的个体为第t代的最优个体。在产生新一代种群后，若迭代达到最大迭代次数，则停止迭代，否则重新执行步骤b到步骤d。迭代结束后，末代的最优个体即为差分进化算法所获得的优化问题最优解。

4 实验验证

为了验证本文所提出的基于差分进化算法的手眼标定方法(以下简称为差分进化算法)的有效性，搭建了机器人相机实验平台进行手眼标定实验验证，如图2所示。实验使用的机器人为UR10六自由度工业机器人，使用的相机为大恒MER-131-75GM/C单目工业相机，相机通过连接件固连于机器人末端执行器。采用的标定板为8×7栅格的棋盘格标定板，每个棋盘格的边长为25 mm，如图3所示。

图2 实验平台 图3 采样的标定板图像

(21)

使用前18组齐次变换矩阵AN和BN(N=1,2,…,18)进行手眼标定，确定相机坐标系到机器人末端坐标系之间的变换矩阵X。使用后6组齐次变换矩阵AN和BN(N=19,20,…,24)对算法求得的变换矩阵X进行验证。在确定手眼标定目标函数时，设定权重系数λ=1。在使用差分进化算法求解时，根据推荐的参数选取方式[15]，设定个体数量M=30，变异因子F=0.5，交叉因子CR=0.9，最大迭代次数为100。根据先验知识，设定种群的上界向量xU和下界向量xL为

(22)

计算得到的齐次变换矩阵X为

(23)

为了验证该方法的有效性，以Zhao[12]提出的正交矩阵形式凸优化方法(以下简称为凸优化方法)进行对比。定义变换矩阵AN(N=19,20,…,24)的估计值为

(24)

相应地，定义估计AN时的平移误差和旋转误差为:

(25)

(26)

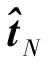
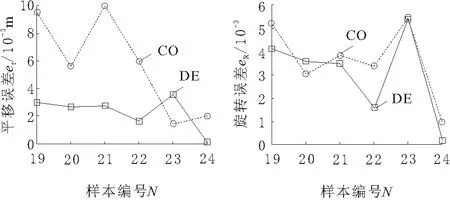
图4 不同样本的平移误差 图5 不同样本的旋转误差

5 结束语

利用李群李代数理论，将手眼标定问题转化为针对误差函数的优化问题，通过对目标函数使用差分进化算法，实现优化问题的求解。借助李代数与李群的对应特性，该方法能够保证求解得到的齐次变换矩阵X落在SE(3)上。利用差分进化算法，避免了该方法在求解过程中落入局部最优。最后搭建手眼标定实验平台，与其他方法进行对比实验。实验结果表明，本文所述方法在平移误差估计和旋转误差估计上均能达到较高的精度，验证了本文所述方法的可行性和有效性。