基于人体参数的被动步行机器人模型及其运动特性分析

楼 飞，沈 巍，关 静，倪国林

(南京师范大学中北学院，江苏 镇江 212300)

0 引言

被动步行机器人因其具有高效，自然的行走步态，开始成为“仿人”步行领域的一大研究热点。这种独特的行走模式有利于深入揭示人类步行机理，并为助步设备的研制提供了新的思路。从90年代McGeer最早提出的对称二维被动步行机器人结构开始，到如今康奈尔大学的“Steven”，代尔夫特大学的“Denise”，吉林大学的“PADW-JL”一代、二代等形形色色的被动步行机器人，诸多国内外高校对被动力学在仿人步行中应用的研究正在如火如荼地开展。然而，目前对被动步行机器人的研究，大都是从如何让它具备更高的局部稳定性和鲁棒性的角度出发，以稳定性分析的结果作为参数优化的依据。通过这种方式得到的被动步行机器人模型对行走初值敏感度较低，同时具备一定的抗干扰能力。但是，这种机器人结构的“仿人”程度有限，离走向实用化阶段还有距离[1-3]。

随着科学技术蓬勃发展，从20世纪60年代开始，通用电气公司最先开始从事外骨骼技术的研究[3]。到如今，诸多国内外科研机构、高校、企业对用于康复治疗或是提升自身能力的助步设备展开了深入的研究。然而这些以外骨骼形式进行穿戴的助步设备，和主动式步行机器人类似，需要对每个关节进行主动控制。这种结构难免会存在效率低，控制复杂，续航能力差的缺陷[4-5]。

本文从实用化的角度出发，着眼于开发被动式助步设备的创意，旨在发掘被动力学在仿人步行领域的应用价值。创新性地提出一种基于人体参数的被动步行机器人动力学模型，并进行求解和分析。最后，根据实际需要，设计一套高度仿人的被动步行机器人三维模型。这种基于人体参数的被动步行机器人，充分利用了被动力学相关原理，有助于实现一种高效，节能，控制简便的助步设备[6]。

1 机械系统整体设计

1.1 人体参数模型

目前，可以通过CT扫描和图像测算的方法得到较为准确的人体特征参数。归纳总结已有文献，可以得出身高为172 cm(取平均身高)，体重为65 kg的中国男性人体参数模型，相关参数如表1所示。

表1 人体各个体段相关数据表

1.2 被动步行机器人参数模型

结合人体参数模型，提出一种包含膝关节、手臂、躯干的被动步行机器人模型。该模型用于指导后面章节中动力学建模与分析，以及机械系统详细设计的进行。如图1所示，是被动步行机器人机械系统整体设计示意图。

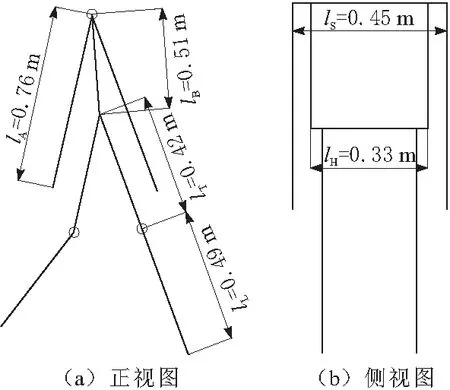
图1 被动步行机器人整体设计示意

由图1可知，基于人体参数的被动步行机器人是一个结构简单的7杆模型。其中字母代号的含义为：A为手臂；B为躯干；T为大腿；L为小腿；S为肩宽；H为髋宽。考虑到被动步行机器人设计的初衷(为助步设备的研制提供新创意)，同时为了限制系统自由度个数，将人体参数模型中的部分体段进行合并。其中包括：上臂、前臂和手进行合并；头、颈忽略；小腿和足进行合并。除此之外，将手臂的运动和异侧大腿的运动进行耦合，躯干的运动始终保持在大腿的角平分线上。整个系统只有髋关节和2个膝关节，共3个自由旋转副。

2 动力学建模与分析

在被动步行机器人动力学建模方面，拉格朗日法一直受到青睐。它从能量的角度出发，结合状态变量，能够构建出形式规整的动力学模型。但是，针对多自由度系统构建动力学方程的过程中，需要对状态变量及其导数求偏导，这里的计算和推导过程十分繁杂，且不利于使用计算机编程。鉴于以上原因，本文将采用空间算子代数相关理论[7]构建动力学模型，并进行局部稳定性分析。以此来探究这种被动步行相关理论能否应用于助步设备的研制中。

2.1 动力学建模

动力学建模的行走模型如图2所示。针对图2和动力学建模中的假设，有几点说明如下。

a.如图2b所示，根据行走状态的不同，将行走过程分为4个相态。从相态1到相态4分别为：3自由摆动状态，膝关节锁合状态，2自由度摆动状态和足-地碰撞状态。

b.采用空间算子代数的方法进行动力学建模，依照D-H法相关原则构建坐标系。如图2a所示，∑I为惯性坐标系，∑i为参考坐标系。刚体的标号采用逆向标注的原则：基座的标号为n+1，与基座相连的刚体为n，末端刚体的标号为1，末端执行器端点为0。

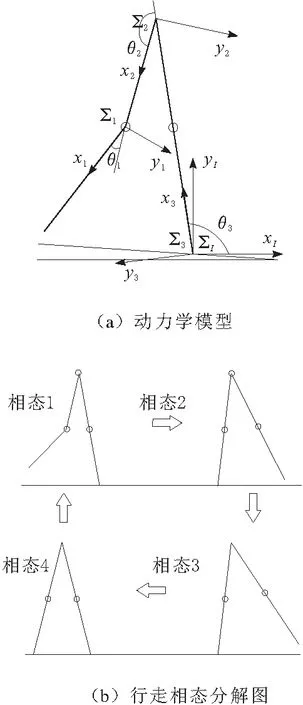
图2 被动步行机器人行走模型

2.1.1 摆动相态动力学建模

根据空间算子代数相关理论，将递推算法引入到动力学建模的过程中。避开了繁杂的推导过程，且有利于计算机编程，提高了求解效率，基本算子如表2所示。

表2 部分基本空间算子简述

空间速度递推表达式为

(1)

空间加速度递推表达式为

(2)

空间力递推表达式为

f(n)=Φ(n,n-1)f(n-1)+m(n)α(n)+b(n)

(3)

由于受篇幅限制，具体的求解过程就不再详述，读者可根据文献[8]自行推导。

最终通过构建相应的空间算子能够得到动力学方程的标准形式为

(4)

2.1.2 碰撞相态动力学建模

利用角动量守恒定律，建立碰撞相态的动力学模型。

膝关节碰撞相态。系统相对于足地接触点O1，摆动腿相对于髋关节H的动量矩守恒，用L及下标表示相态矩阵，则

(5)

足地碰撞相态。系统相对于足地接触点O2，摆动腿相对于髋关节H，摆动腿小腿相对于膝关节K的动量矩守恒，用L及下标表示相态矩阵，则

(6)

式(5)和式(6)中的上标“+”和“-”分别代表对应状态变量在撞前瞬间和碰撞后瞬间。

2.2 运动特性分析

被动步行机器人能否进行稳定步行，是考量其实用性的重要指标。在动力学建模的基础上建立庞卡莱映射函数，结合牛顿-拉夫逊迭代法则，求解不动点x，并构建不动点x处的雅克比矩阵J(x)。最终利用floquet乘子法[9]来求证该被动步行机器人是否具有稳定步行的能力(具有局部稳定性[10])。整个运动特性分析流程如图3所示。雅克比矩阵J(x)如式(7)所示。

(7)

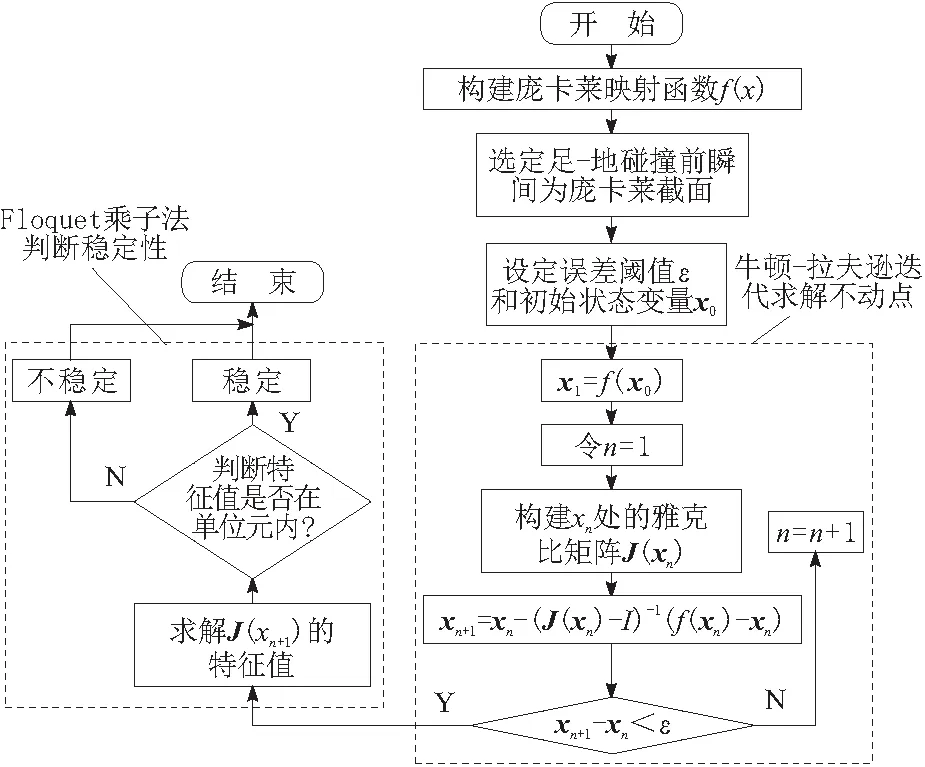
图3 运动特性分析流程

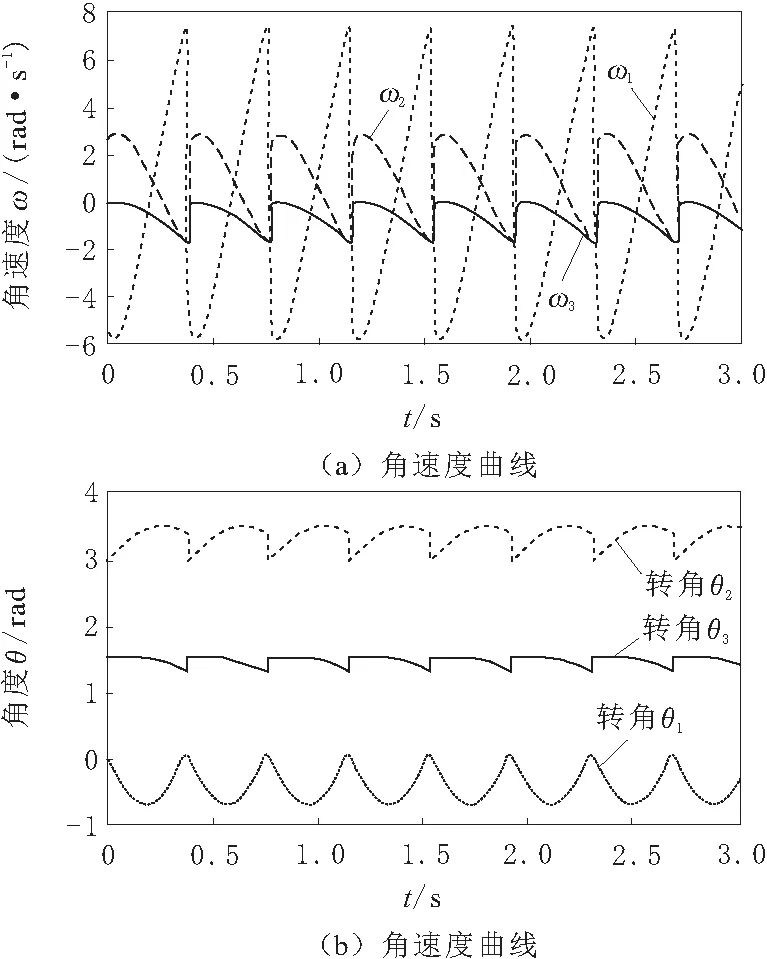
图4 运动特性曲线

从图4可以看出，该被动步行机器人以不动点为初始条件，能够以一个稳定的周期进行被动步行，不存在周期分岔现象。

3 机械系统详细设计

通过前面章节的分析，可以初步认定基于人体参数的被动步行机器人能够实现稳定行走。然而，动力学建模和分析是在理想情况下进行的，和实际情况具有差距。为了进一步将“被动力学”的应用价值体现出来，需要对这种基于人体参数的被动步行机器人进行机械系统详细设计，为虚拟样机仿真实验提供便利。根据图1整体设计的理念，本文将被动步行机器人的设计过程分为髋关节设计、膝关节设计、踝关节设计、足部设计和总装。

3.1 髋关节设计

躯干的引入能够增加被动步行机器人行走的稳定性。为了不增加额外的自由度，将躯干的运动限制在大腿夹角的角平分线上。与此同时，引入手臂除了提高仿人程度，还具有增加行走平衡性，削弱偏航的作用。手臂的运动和异侧大腿的运动应该保持一致。为了实现以上功能，需要设计一种集成“角平分机构”和“大腿-手臂耦合机构”的髋关节结构。髋关节机械系统如图5所示。

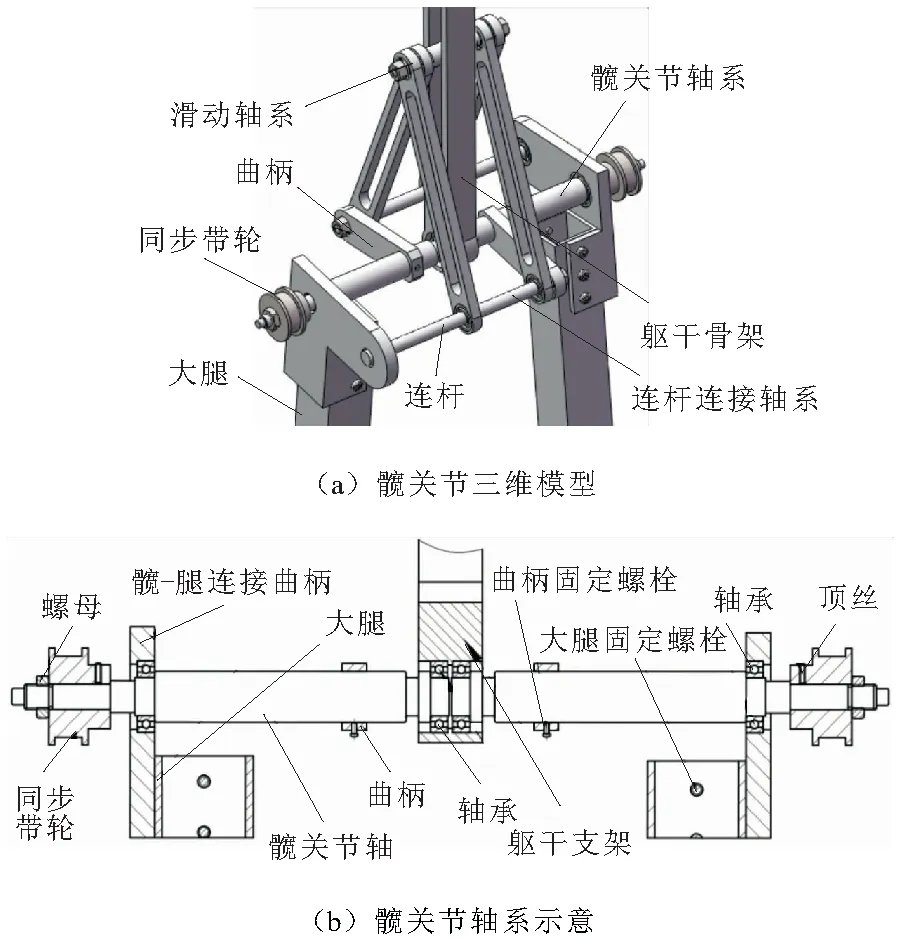
图5 髋关节机械系统

被动步行机器人髋关节的三维模型如图5a所示。由图5a可以看出，该机构通过2组曲柄滑块机构联动的方式将躯干的运动限定在大腿的夹角平分线上。如图5b所示，髋关节轴系由2根断开的髋关节轴组成，髋-腿连接曲柄可以绕髋关节轴旋转，通过连杆轴系和曲柄连接。曲柄和髋关节轴固连，将一侧大腿的运动传递到另一侧的髋关节轴上。髋关节轴上固连1个同步带轮，该同步带轮会带动和手臂轴固连的同步带轮转动，从而实现和手臂运动的耦合。

3.2 膝关节设计

根据图2b，被动步行机器人行走相态分解图可以明确，稳定的行走状态需要膝关节的相关节动作配合实现。本文所设计的被动步行机器人采用了一种最简单的膝关节结构，利用电磁铁通、断电实现膝关节的放开和锁合。膝关节的三维模型如图6所示。

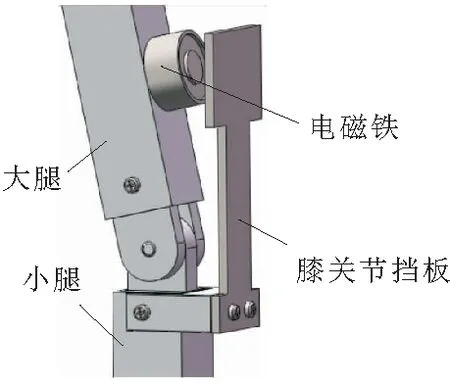
图6 膝关节三维模型

结合行走过程对膝关节的动作简述如下：支撑腿的膝关节锁合，支撑腿上的大腿和小腿不会发生相对旋转；此时，摆动腿的膝关节放开，进行自由摆动，系统为3自由度；当摆动腿上的小腿和大腿摆动到同一条直线上时，即膝关节发生碰撞，电磁铁通电，摆动腿膝关节锁合，系统变为2自由度双直腿结构并继续摆动；当足底曲面板和地面发生碰撞之后，微摆动腿和支撑腿角色互换，原支撑腿的膝关节打开，此时又变回3自由度摆动。

3.3 踝关节和足部设计

基于人体参数的被动步行机器人采用不完全对称的双足结构。通过研究表明，这种结构的机器人在行走过程中会发生“偏航”。当单腿支撑时，摆动腿一侧重，会产生绕支撑点的旋转力矩，导致该机器人不能以直线行走。为了避免“偏航”，并提升机器人的行走能力，需要对踝关节和足部的结构进行特殊的设计。采取的主要措施包括：

a.用1个十字联轴器连接小腿和足部，联轴器四周用对抗弹簧拉紧，形成1个具有柔性的踝关节结构。机器人在行走过程中，沿冠状面分布的弹簧会根据受力不同产生不同的压缩量，使压力中心产生左右波动，对“偏航”起到削弱作用。足部触地瞬间开始，沿矢状面分布的弹簧发生形变，进行储能，足部离地瞬间，弹簧力会使机器人产生蹬地动作，加快摆动腿的摆动。

b.采用如图7所示的特殊足部形状，对行走过程进行引导。该足底在矢状面和冠状面的投影都是一个圆弧形。这种结构使得被动步行机器人在行走过程中同时具有矢状面和冠状面的运动。可以有效避免足部发生“擦地”的现象。

c.在足底安装防滑橡胶垫，提升足-地接触面的摩擦系数，增大摩擦力，削弱偏航现象。

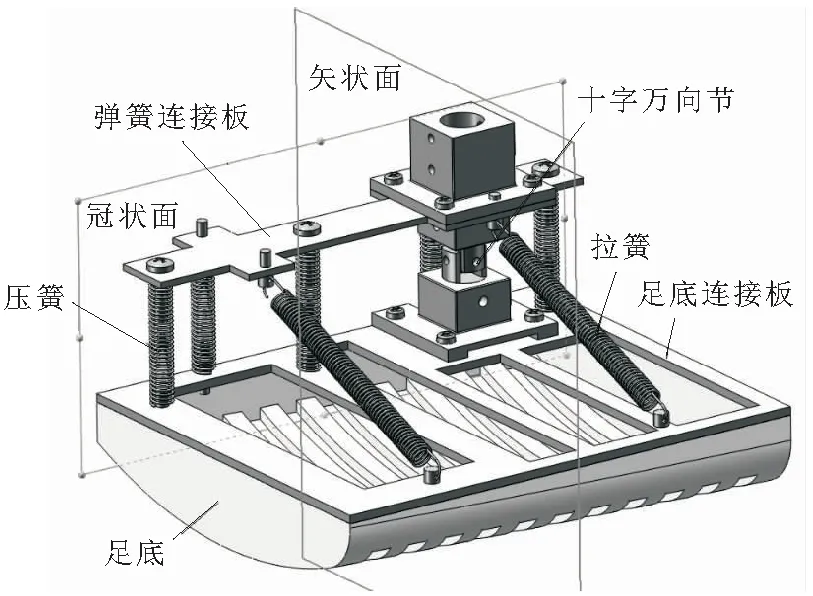
图7 踝关节和足部三维模型

3.4 整体结构

根据之前章节的铺垫，提出一种基于人体参数的被动步行机器人三维模型，如图8所示。

图8 整体结构

整体结构主要包括:驱壳、大腿、小腿、手臂、膝关节、髋关节、踝关节和足部。结构尺寸按照机械系统整体设计的要求进行。

4 虚拟样机仿真实验

前面章节给出了被动步行机器人的详细三维模型，本章利用ADAMS建立虚拟样机模型，以更接近实际的虚拟实验环境对这种基于人体参数的被动步行机器人行走机理进行验证。如图9所示，是基于人体参数的被动力学机器人在ADAMS仿真环境下的行走仿真图。

图9 ADAMS虚拟样机仿真示意

5 结束语

利用空间算子代数相关理论进行动力学建模和局部稳定性分析发现，基于人体参数的被动步行机器人具有稳定走下斜坡的能力，从理论上验证了“被动力学”在仿人步行领域的研究价值。为了从实用化的角度展现“被动力学”在助步设备研制过程中的应用价值，针对本文所研究的被动力学机器人进行了机械系统详细设计，建立其三维模型并进行虚拟样机仿真实验。

综上所述，本文给出一种基于人体参数的被动步行机器人模型，并对其运动特性展开了较为全面的分析。最终结果不仅为实物样机的研制奠定了基础，还给被动步行机器人的参数优化提供了新的方向，对被动式助步设备的研制也起到了推动作用。