基于同态加密的多分类Logistic回归模型*
2020-05-09许心炜
许心炜,蔡 斌,向 宏,桑 军
1.信息物理社会可信服务计算教育部重点实验室(重庆大学),重庆400044
2.重庆大学大数据与软件学院,重庆400044
1 引言
机器学习是人工智能的核心技术,研究计算机如何模拟或实现人类的学习行为,以获取新的知识或技能.机器学习可以自动地产生模型,分析更大的数据,解决更复杂的问题.随着计算能力的发展,机器学习应用范围也在不断扩大.然而,如何保护数据的隐私已经成为一个重要问题,尤其对于医疗、基因、财务等特别注重个人隐私的数据.
传统加密系统依赖于交换加密信息的双方之间共享密钥.但是,这种方法存在隐私问题.用户会失去对敏感数据隐私的控制,尤其在现今流行的云服务中.Nikolaenko等[1]基于 Yao的Garbled Circuit[2]提出了一种隐私保护线性回归协议.Mohassel等[3]将安全多方计算应用于隐私保护机器学习中.但是这些方法需要所有的参与方都遵照协议才能保证方案的安全性和正确性.因此,这些方法虽然实现了安全多方计算,但是并不是完全安全的外包计算方案.
同态加密是一种特殊的加密方案,它允许第三方对加密数据进行操作,而不需要事先对其进行解密,并且得到的运算结果解密后与在明文上运算结果一致.因此同态加密是有效保护用户隐私的一项技术.Graepel等[4]讨论了使用同态加密进行机器学习的适当和不适当的场景,提供了线性均值分类器和线性判别分析两个例子,这两个例子均可以在同态加密中使用低次多项式来实现.然而,这些简单的参数模型不能很好地处理复杂的数据集,同时也不是生物医学研究中使用的主流机器学习技术[5].Xie等[6]使用加法同态加密方案来汇总一些中间统计数据,然而计算中间信息需要昂贵的计算成本.Crawford等[7]在训练小型Logistic回归模型方面取得了良好的表现,但是他们的解决方案只允许计算特征非常少的数据.
与本文最相似的是Kim等[8]和 Chen等[9]的工作.2017年iDASH安全基因组分析竞赛中,Kim等[8]提出了一个基于有效近似算术同态加密的安全Logistic回归模型.Chen等[9]在完全同态加密中应用了多位明文空间以及定点数编码,提出了基于SEAL库的加密Logistic回归模型.
但是,这两种解决方案只能分析二分类问题,而现实生活中存在许多多分类问题.本文基于 Kim等的研究以及Sánchez-Maroño等[10]的针对多分类情况的OVR方法,提出了一种基于同态加密的多分类Logistic回归模型.该模型可以在解决多分类问题的同时保证数据的隐私安全.该模型具有良好的性能,输出的结果可以与未加密运算输出的结果一致,不影响模型的准确率.
2 相关技术
2.1 HEAAN方案
同态加密是一种加密技术,允许我们在不解密的情况下对加密数据进行操作,并得到与明文计算相匹配的计算的结果.该技术在实际应用中具有很大潜力,因为它允许我们在公共却不信任的服务器上安全地进行外包计算.
Cheon等提出了一种方法,构造近似数算术同态加密方案,简称为HEAAN方案.HEAAN方案支持加密消息的近似算术,使得参数的大小不会增加过多,减小了一定的精度而大幅提高效率.HEAAN方案支持密钥生成、加密、解密、加法和乘法等操作.同时,该方案支持消息打包,这有利于实现并行化.
HEAAN方案的主要思想是将加密噪声视为近似计算过程中出现误差的一部分.即,给定私钥 sk和密文模数q,对于小的误差e,一个明文m的密文c满足
HEAAN方案是以LWE(Learning With Errors)问题为理论基础.对于2的整数幂N,模数为N的分圆多项式定义为R=Z[X]/(XN+1).对于一个正整数q,R模q的剩余环定义为Rq=R/qR.下面是对HEAAN方案操作的简要描述:
•参数设置(λ):输入安全参数λ,输出多项式维度N,最大密文模数q和离散高斯分布χ.
• 密钥生成 (N,q,χ):输入参数N,q,χ,取样s←R,a←Rq,e←χ,输出私钥 sk←(1,s)和公钥pk←(b,a)∈Rq×Rq,其中b←−as+e(modq).设Q=q2,取样s′←s2,a′←RQ,e′←χ,输出计算密钥 evk←(b′,a′)∈RQ×RQ,其中b′←−a′s+e′+qs′(modQ).
• 加密 (m,pk):输入明文m∈R,取样v←χ,e0←χ,e1←χ,输出密文m←v·pk+(m+e0,e1)(modq).
• 解密 (c,sk):输入密文c=(c0,c1),输出m←c0+c1·s(modq′).
• 加法 (c,c′): 输入密文c,c′,输出cadd←c+c′(modq′).
• 乘法 (c,c′,evk): 输入密文c= (a0,b0),c′= (a1,b1),设 (d0,d1,d2)= (b0b1,a0b1+a1b0,a0b1)(modq′),输出cmult←(d0,d1)+⌊1/q·d2·evk⌉(modq′).
• 重缩放 (c,p):输入密文c和一个 2的整数幂p,输出c′←⌊1/p·c⌉(mod(q′/p)).
•旋转(c,rk,r):输入密文c和旋转密钥rk,输出c的明文向量旋转r个位置后的密文c′.
有关HEAAN方案的技术细节和噪音分析可以参考文献[11].有关HEAAN方案的bootstrapping方法可以参考文献[12].
2.2 Logistic回归和梯度下降
Logistic回归是机器学习中常用的一种方法,用于建立一个可区分 2个或更多类别样本的模型.Logistic回归的一种常见形式是表示为类别0的后验概率:
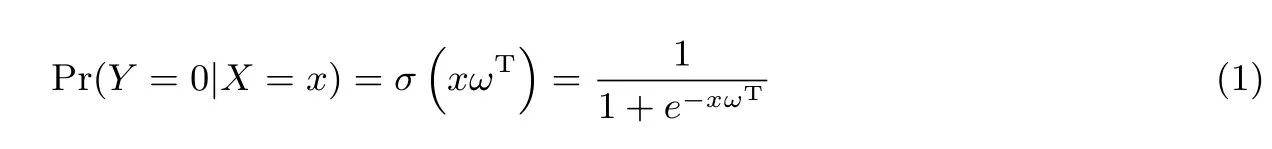
其中,Y表示类别,x∈Rf表示特征,ω∈Rf表示在模型训练中需要学习的权重向量,σ(t)=1/(1+e−t)是sigmoid函数,将xωT转为后验概率.
机器学习中,损失函数是用来了衡量模型的预测值和真实值的一致程度,损失函数越小,模型越优.对于Logistic回归,使用极大似然估计法,可以得到损失函数:

其中,n表示样本数量.
训练Logistic回归的常用方法是梯度下降法.梯度下降的计算过程是沿着梯度下降的方向求解损失函数的最小值.梯度在每次迭代中下降,第t次迭代中权重向量ω更新为:

其中,α表示学习率.
动量法改进了梯度下降法.动量法使得每一次的参数更新方向不仅仅取决于当前位置的梯度,还受到上一次参数更新方向的影响.而Nestervo梯度下降法[13]相比动量法,添加了误差微分量,使其具有更快的收敛速度.设初始量v0=ω0,Nestervo梯度下降法更新方程如下:

其中,0<γ<1表示衰减率.
2.3 Sigmoid函数的近似多项式函数
虽然梯度下降法比其他的训练方法更适合同态计算,但现有的同态加密只能支持多项式算术运算,所以计算sigmoid函数成为了一个计算的阻碍.
Chen等[9]使用了极小极大方法[14]得到了sigmoid函数在区间[−5,5]上的3次多项式近似函数:

Kim等[15]使用了最小二乘法找到了sigmoid函数在区间[−8,8]上的3,5,7次多项式近似函数.
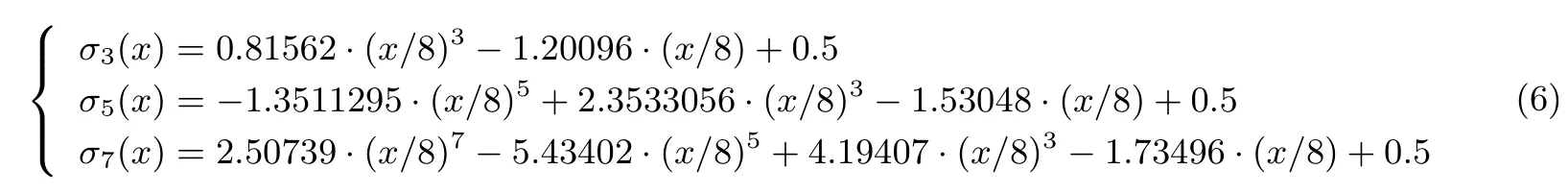
区间范围内,低阶多项式只需要较小的计算深度,具有较高的效率,而高阶多项式则具有较高的精度.本文采用了Kim等的近似方法,并在效率和精度中做了权衡,使用5次多项式进行同态计算.
3 同态加密多分类Logistic回归模型
3.1 多分类 Logistic回归
Logistic回归也可以完成多分类学习任务.本文基于拆解方法中的“一对其余”(One vs Rest,OvR)策略,扩展二分类Logistic回归模型来解决多分类问题.
给定数据集D={(x1,y1),(x2,y2),···,(xn,yn)},yi∈C1,C2,···,Ck.OvR 策略每次将一个类的样例作为正例,剩余其他类型的样例作为反例训练出k个分类器,得到{P1,P2,···,Pk}.比较各个分类器的预测置信度,选择最大置信度对应的标记类别作为预测的分类结果.OvR策略的详细过程如图1.

图1 OvR策略示意图Figure 1 Diagram of OvR strategy
OvR策略只需要训练k个分类器,相对其它拆解方法,存储和测试时间开销通常较小.使用OvR策略得到的多分类Logistic回归的详细过程如算法1.

算法1多分类Logistic回归算法Input:X ∈RN×F,y∈RN,α>0 Output:ω ∈ RK×F 1初始化权重矩阵ω;for iter=0 to T do 2 for k=0 to K do 3 for i=0 to N do 4 Pi←
3.2 多分类 Logistic回归的同态计算
本节将描述如何基于HEAAN方案,对加密数据进行安全的多分类Logistic回归运算.
在同态加密的外包计算模型中,客户端加密数据,服务器对加密后的数据进行同态计算,并返回计算结果给客户端,最终由客户端对结果进行解密.
在本文的模型中,首先,客户端将大小为n×(f+1)的数据集X和初始化后的权重矩阵ω加密后并发送给服务器.根据公式(3),要先进行内积计算.
HEAAN方案中没有直接的内积计算方法,需要通过乘法、加法、旋转运算构造内积计算.对每个类别的权重向量,首先对其进行N次复制填充槽,然后与数据集的密文做对位乘法运算.接着通过旋转相加得到内积.但此时内积中含有无价值的数据,将其与常量矩阵相乘,可得到完整的内积.常量矩阵是第一列向量为1,剩余列向量为0的矩阵.详细的内积计算方法如算法2.

算法2内积计算Input:数据集矩阵X 加密后的密文CX,权重向量ωk加密后的密文Cωk,常量矩阵M 加密后的密文CM Output:内积矩阵密文CI 1将Cωk复制N 次填充槽,得到矩阵密文Cω;2C1←Rescale(CMult(CX,Cω),p);3for i=0 tolog(f+1)−1 do 4 C2←Add(C1,Rotate(C1,2i));5end 6C3←Rescale(Mult(C2,CM),pc);7for i=0 tolog(f+1)−1 do 8 CI← Add(C3,Rotate(C3,−2i));9end 10return CI
得到内积后,使用Sigmoid近似函数进行计算.根据公式(3),得到的结果与标签矩阵密文进行同态减法,再与数据集矩阵密文做同态乘法.将结果进行旋转相加,再乘以学习率,可以得到梯度值.将权重与梯度值做同态减法,可以得到更新后权重值的密文.完整的密文的多分类Logistic回归算法如算法3.
做多次迭代后,服务器得到最终的权重矩阵的密文并将其发送给客户端.客户端进行解密操作,可以得到更新后的ω′并对其他数据进行预测.
在整个过程中,服务器只对密文进行操作而不能看到任何明文.客户端可以使用服务器的计算能力而不泄露隐私,并且能得到更新后的权重矩阵,解决多分类问题.可见,基于同态加密的多分类 Logistic回归模型是安全且有效的.

算法3密文的多分类Logistic回归算法Input:数据集矩阵X 加密后的密文CX,权重矩阵ω加密后的密文Cω,标签矩阵Y 加密后的密文CY,α>0 Output:权重矩阵密文Cω′1for iter=0 to T do 2 for k=0 to K do 3 C1←InnerProduct(CX,Cωk);4 C2←PolySigmoid(C1);5 C3←Sub(C2,CY);6 C4←Rescale(Mult(C3,CX),p);7 for i=log(f+1)−1 to log(f+1)+logn−1 do 8 C5←Add(C4,Rotate(C4,2i));end 10 C6← Rescale(α ·C5,pc);11Cω′k←Sub(Cωk,C6);12 end 13end 14return Cω′9
4 实现
本文的实现基于Cheon等实现HEAAN方案的开源库[16].所有的实验都在Intel core i5 4200 M 2.5 GHz机器上实现.
本文使用了来自UCI的Dermatology数据集[17]和Iris数据集[18]来测试本文的模型的性能.Dermatology数据集研究的是红斑鳞状疾病的鉴别诊断,是皮肤病学的一个现实问题.红斑鳞状疾病的临床特征差别小,具有许多组织病理学特征,因此难以鉴别诊断.该数据集包含358个样本,每个样本包含34个特征,共分为6类.Iris数据集是常用的分类实验数据集,包含150个样本,每个样本包含4个特征,共分为3类.
为了证明方法的有效性,使用了5倍交叉验证方法,将数据集随机分为5个大小相等的子集,并将其中4个子集用于训练,剩余 1个子集用于测试模型.由于迭代次数越高,需要的计算开销越大,所以将同态加密下的模型的迭代次数设为7次.表1列出了分别对明文和加密数据进行计算的模型的性能,包括平均运行时间(加密和计算)和准确率.

表1 使用5倍交叉验证的模型的实验结果Table 1 Implementation results for model with 5-fold CV
根据实验结果,可以看出,模型使用Sigmoid原函数进行计算时,由于不考虑开销问题,通过增大迭代次数,可以达到较高的准确率.同样使用Sigmoid近似函数进行计算时,模型对加密数据训练得到的准确率与对未加密数据训练得到的准确率相同,由此可以验证本文模型同态计算的可行性.虽然,对加密数据的训练速度比对未加密数据的训练速度相比慢得多,但是训练一次得到的结果可以用于多次预测,所以针对注重隐私性的医疗、基因、财务等数据而言,对加密数据的训练速度是可以接受的.
5 总结
本文提出了一个解决方法,基于近似同态加密方案,实现了安全的多分类 Logistic回归计算模型,并针对Dermatology数据集和Iris数据集对模型进行了评估.本文的模型表现出较好的性能,Dermatology数据集36.70分钟的训练时间验证了模型在现实应用中的可行性,同时模型准确度与未加密情况下计算的准确度一致.
在未来的工作中,可以使用本文的思路和技术,将同态加密应用于其它机器学习算法.同时应用HEAAN方案的bootstrapping方法解决较大迭代次数导致的计算开销问题.
