基于NTRU的单向抗合谋代理重加密方案*

2020-05-09张明武

密码学报 2020年2期

关键词：合谋私钥公钥

张明武,杜林

1.湖北工业大学计算机学院,武汉430068

2.密码科学技术国家重点实验室,北京100878

3.广西密码学与信息安全重点实验室,桂林541004

1 引言

代理重加密是一种非对称公钥加密体制,一个半可信的代理使用重加密密钥将授权者公钥加密的密文转换成可用被授权者私钥解密的密文[1,2].这一转换特性使其在公钥加密领域得以大展身手,如在分布式文件系统、数字版权保护、加密垃圾邮件过滤、云计算中的应用等,使用云服务器作为半可信代理人进行代理重加密过程如图1所示.而为了实现代理重加密方案,则需要给代理者一个重加密密钥,但在重加密密钥的设计中需要考虑的是,防止代理者与被授权者合谋获得授权者的私钥或代理者与授权者合谋获得被授权者的私钥,最重要的是要保证被授权者解密的正确性.

最初的代理重加密方案是由Blaze等人[2]在欧洲密码学年会上提出的,但是该方案无法抵抗合谋攻击,即被授权者能与代理者合谋获取授权者的私钥,此外该方案是双向重加密的,即代理者既能将A的密文转换成B的密文,也能将B的密文转换成A能解密的密文.Ateniese等人[3]利用双线性配对(bilinear-pairing)构造出首个单向代理重加密方案,该方案是单跳的,且能抗合谋攻击,而且在标准模型下达到了CPA安全,该方案基于双线性对上判定性Diffie-Hellman假设.Canetti和Hohenberger[4]于2007年首次提出了基于标准模型的选择密文安全(CCA)安全双向代理重加密方案,为了达到CCA级别安全性,密文设计中采用了一次性签名方案,但该方案无法抵挡合谋攻击.Liu等人[5]提出了一种用于文件共享系统的多条件代理广播重加密(MC-PBRE)方案,在标准模型中达到了CCA安全,此外,该方案可以抵抗合谋攻击.Paul等人[6]提出一种新的抗共谋 IB-PRE方案,该方案是基于 Diffie-Hellman假设,且在随机预言机模型下达到了自适应CCA安全性[7].

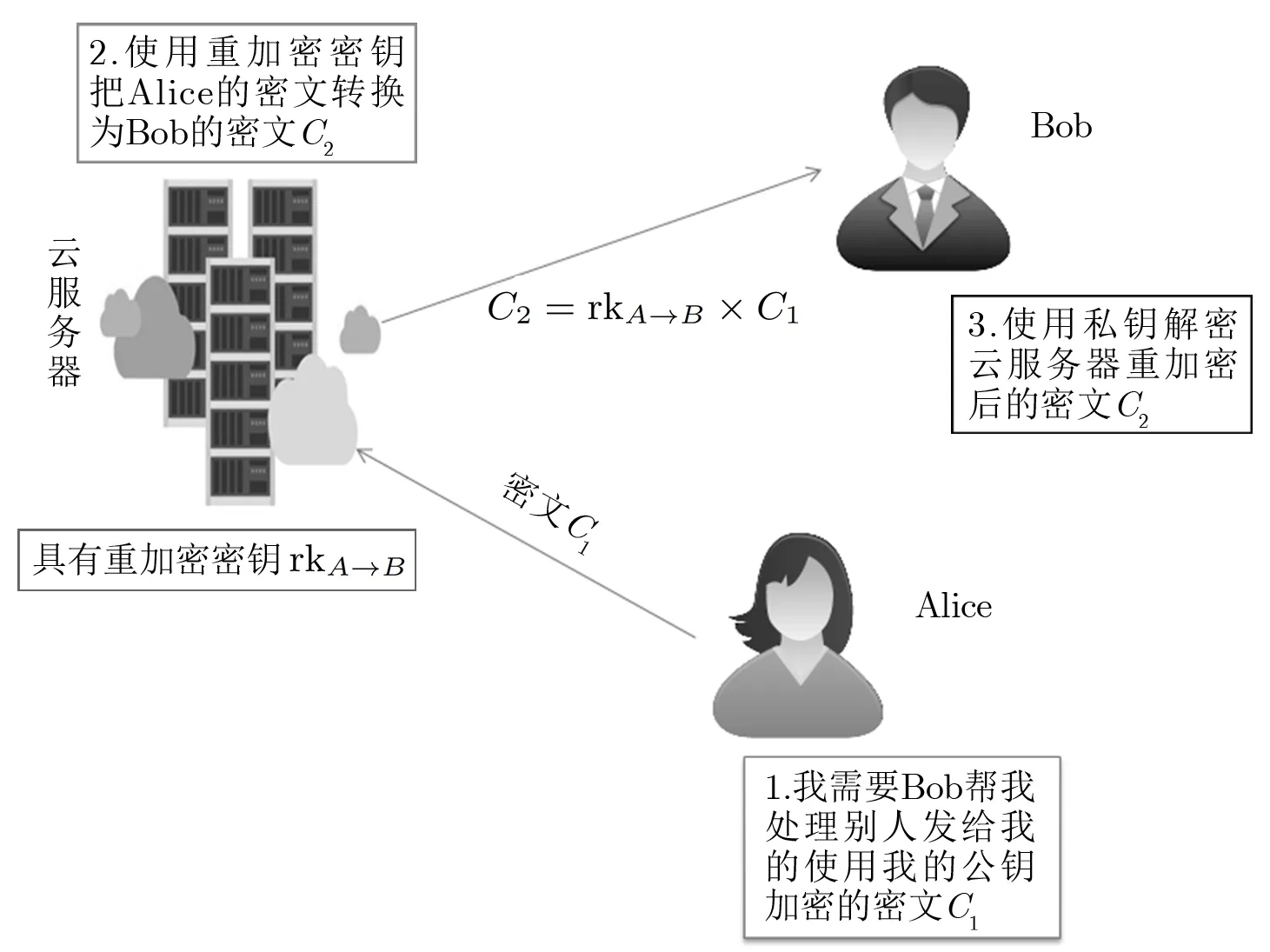
图1 云服务器代理重加密Figure 1 Cloud-server based proxy re-encryption

以上方案的安全基础都是基于数论中的大素数因子分解、离散对数或双线性群上的困难问题假设.1994年美国贝尔实验室的科学家 Peter Shor提出了一种破解上述困难问题的算法[8],从理论上证明了这种算法可以在极短的时间内破解上述问题,虽然其前提条件是大规模量子计算机的使用,但随着量子计算机技术的快速发展,这种破解的可能性正在极速变大.因此,研发针对量子攻击的公钥加密技术刻不容缓.所幸的是,学界已经研究出了数种抗量子密码,它们大体上可以分为四类,即基于编码的算法(Codebased)、基于多变量多项式的加密算法(Multi-variable polynomial)、基于安全散列函数的算法(Secure Hash-based),以及格基加密算法(Lattice-based).其中,基于格密码系统在过去十年中得到了最为广泛的关注.与大素数分解和离散对数问题不同,目前还没有量子算法可以借助量子计算机在多项式时间内对其进行破解,而且,格密码系统在最坏情况假设条件下依然具备安全性.

在现有公钥密码系统中,例如RSA公钥加密体制,它的安全性是来自生成密钥需要选择2个既是质数又能形成分解困难问题实例的随机大数,但是在这个过程中存在选择错误数字而导致安全性下降的可能性.而在格密码系统中,所有可能的密钥选择方式都能够形成足够的困难性.基于格有两个经典的困难问题,一个是最短向量问题 (Shortest Vector Problem,SVP),即在格内找到最短的非零向量,另一个是最近向量问题 (Closet vector problem,CVP),即在格中找到一个距离目标向量最近的非零向量.目前,NTRU(Number Theory Research Unit)加密体制以及基于带错误学习问题 (Learning With Error,LWE)[9]的加密方案是基于格密码系统发展实用前景最好的两种加密算法.Hoffstein、Pipher和Silverman[10]于1996年提出首个基于格的NTRU加密体制.从那时起,它一直是最实用的基于格的公钥密码体制,并被IEEESTD 1363.1-2008[11]和ANSI X9.98-2010[12]标准化.NTRU得到广泛研究和应用的另一个原因是它相对于传统的公钥密码系统来说,具有十分显著的计算性能优势[13].例如,在GPU上分别执行NTRU、RSA和ECC,效率上比较:NTRU比RSA快1000倍,比ECC快100倍[14].NTRU高效的原因可以由其底层操作的简单性来解释,NTRU算法中使用系数相对较小的多项式,运算操作为加法和卷积乘法,即使在约束器件中也可以有效地执行运算操作[15].随后一些基于格上的加密体制纷纷被提出,如Aono等人[16]设计一种新的基于LWE困难问题的代理重加密方案,该方案在标准模型下达到了CPA安全,且具有单向性和多跳性.

基于NTRU密码体制的安全性可被规约为最坏情况下的格困难问题,即安全性是基于最坏情况假设的.这和传统基于平均情况下困难问题的加密体制相比较,能够在安全性上给予进一步的保障,安全性可以规约到最短向量问题.Nnez[17]等人提出了第一个基于NTRU的代理重加密方案,但提出的方案是双向重加密的,且不能抵抗被授权者与代理者或授权者与代理者之间的合谋攻击.

本文贡献:本文在Nnez等人方案的基础上提出一种新的基于NTRU的代理重加密方案.本文方案对比原方案有以下几个方面的优势:一是能够抗合谋攻击.在原方案中代理者与被授权者可以合谋获取授权者的私钥或是代理者能与授权者合谋获取被授权者的私钥,而本方案中对该缺陷做了改进,使得代理者无法与被授权者合谋获得授权者的私钥,代理者也无法与授权者合谋获得被授权者的私钥.二是设计单向的重加密能力,原方案是双向重加密的,而单向重加密方案比双向重加密的隐私性和安全性更好,主要原因是双向重加密可以由单向重加密构成,反之则不能,我们提出的方案是支持单向重加密.三是本文方案支持多跳性,即代理者具有对密文执行多次重加密运算能力,以实现多次密文代理转换的解密能力.

2 预备知识

2.1 符号定义

本节主要介绍文中所使用的一些符号的具体含义,如下所示.

b列向量n多项式环的维度

q正整数,在加解密过程中减小多项式的系数fp私钥f在模p运算中的乘法逆元

Z 整数域 Z[x]环

Ř 整数系数多项式集合p素数,在加解密过程中减小多项式的系数

Rnn维欧氏空间fq私钥f在模q运算中的乘法逆元

2.2 代理重加密方案的定义

在本节中,首先给出基于Canetti和Hohenberger[4]的重加密方案的基本定义,一个代理重加密由6个多项式时间的算法构成:

方案算法具体功能如下:

算法1代理重加密算法PRE=(Setup,KeyGen,Encrypt,ReKeyGen,ReEnc,Decrypt)• Setup(λ):输入安全参数λ,输出公共参数pp.• KeyGen(pp):密钥生成算法给用户i输出公钥pki和私钥ski.• Encrypt(pkA,m):加密算法的输入为授权者A的公钥pkA和明文m输出则为密文CA.• ReKeyGen(skA,pkB):重加密密钥生成算法输入A的私钥skA和被授权者B的公钥pkB,输出重加密密钥rkA−→B.• ReEnc(CA,rkA−→B):重加密算法的输入为密文CA和重加密密钥rkA−→B,输出则为代理者加密后的密文CB.• Decrypt(CB,skB):解密算法的输入为密文CB和被授权者B的私钥skB,该算法的输出为明文m.

代理重加密方案PRE的正确性满足下面两个条件:

(1)授权者A使用私钥skA解密:

(2)被授权者B使用私钥skB解密:

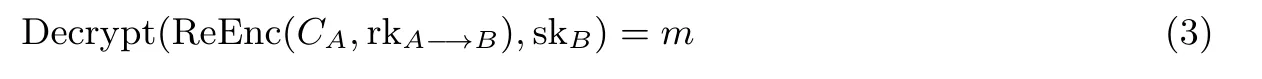
如果以上两种解密算法均能得到正确明文,则可以证明该方案满足正确性要求.

2.3 多跳性

重加密方案满足多跳性:半可信代理者可以多次使用不同的重加密密钥,对密文执行多次重加密运算.下面给出多跳性的具体定义:

算法2代理重加密方案多跳性定义• 第一次加密:用户A由密钥生成算法得到公钥pkA和私钥skA,由明文空间中选择明文m,再由加密运算Encrypt(pkA,m)得到密文C1.• N−1次重加密过程:由密钥生成算法得到一系列公私钥对(pki,ski),其中2≤i≤N,随后由重加密密钥生成算法得到一系列的重加密密钥rkj−→j+1,其中1≤j≤N−1,随后执行N−1次重加密过程:第一次重加密:C2=ReEnc(C1,rk1−→2)第二次重加密:C3=ReEnc(ReEnc(C1,rk2−→3))...第 N −1次重加密:CN=ReEnc(CN−1,rkN−1−→N)第N位接收者执行解密运算Decrypt(CN,skN)→m.

如果第N位接收者执行解密运算后得到结果为m,则证明该方案满足多跳正确性.

2.4 最短向量问题和最近向量问题

设b1,b2,···,bm∈Rn,是一组线性无关的向量,则集合L={x1∗b1+x2∗b2+···+xm∗bm|xi∈Z}为向量b1,b2,···,bm在 Rn中的格,向量b1,b2,···,bm为格L的一组格基.

最短向量问题(SVP):在格L中寻找一个最短的非零向量,即在格L寻找一个非零向量v∈L,使它的欧几里得范数||v||最小.而SVP已经被证明是NP困难问题[18,19].

最近向量问题(CVP):给定一个不在格L中的向量w∈Rn,寻找一个向量v∈L,使它最接近w,即寻找一个向量v∈L,使得欧几里得范数||v−w||最小.

3 本文方案

在本节中,我们首先介绍传统NTRU加密方案,随后给出改进NTRU加密方案的代理重加密方案.

3.1 NTRU 加密方案

NTRU加密体制是由Ho ff stein等提出,算法是基于卷积多项式环Ř=Z[x]/(xn−1)的加密体制,Ř表示最高次数不超过n−1的所有整系数多项式集合,n一般为素数.NTRU体制中别的公共参数还有p和q,p一般选择为3,q一般为2的幂次方,q越大,则方案的安全性越高.一般来说,NTRU体制中的所有运算都是在模q和模p中进行的.NTRU中多项式的运算有加法和乘法,设其中一个元素为:

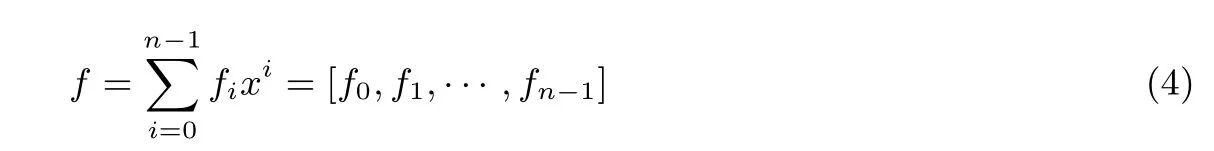
加法运算为:f+g=(f0+g0)+(f1+g1)∗x+···+(fn−1+gn−1)∗xn−1

乘法运算为:f∗g=h,其中,在NTRU算法中定义乘法运算为卷积运算.

在NTRU体制中,私钥sk是由多项式环中随机选取一个多项式(f∈Ř)得到的,私钥的系数一般为0、−1和1,此外,该多项式还需满足以下条件,需要在Ř(modq)和Ř(modp)中分别具有逆元,即存在fq和fp使得私钥满足f∗fq≡1(modq)和f∗fp≡1(modp),则fq和fp就是私钥的逆元.下面给出NTRU的详细算法.

3.2 基于NTRU的代理重加密方案

• 密钥产生 (KeyGen):密钥生成算法的输出是为授权者A,被授权者B分别生成一对公私钥(pki,ski).对于授权者A,首先从Ř中随机选取小多项式fA(即系数一般为0、−1和1),此外,多项式fA要同时满足

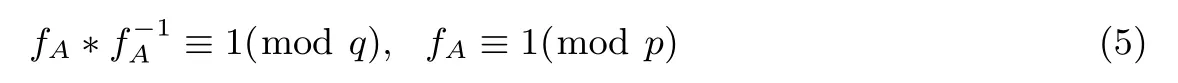
随后再由Ř中随机选取小多项式gA,计算公钥pkA=p∗gA∗(modq),授权者A的私钥就是fA.同理可知被授权者B的公私钥分别为(pkB=p∗gB∗(modq),skB=fB).

•重加密密钥生成算法(ReKeyGen):该算法是基于Nnez等人设计的重加密密钥算法.在原方案中,该算法的输入是授权者A的私钥fA和被授权者B的私钥fB,依据重加密密钥的生成协议,首先由授权者A从Ř中随机选取多项式r′随后发送r′∗fA(modq)给被授权者B,r′发送给代理者C.被授权者B发送r′∗fA∗(modq)给代理者C,代理者C就可以得到重加密密钥 rkA−→B=fA∗(modq),但是原方案设计的重加密密钥无法抵抗合谋攻击,该缺陷在 4.2节会详细介绍.

本方案改进了重加密密钥生成算法.首先,本算法的输入也是授权者A和被授权者B的私钥,分别为fA和fB.首先授权者A从 Ř中随机选取r1和e1,随后授权者A计算a=r1∗(fA+p∗e1)(modq)并将其发送给被授权者B,将r1发送给云服务器C.被授权者B收到a后,计算b=a∗(modq),随后被授权者B将b发送给云服务器C.

在云服务器C收到b和r1之后,计算重加密密钥

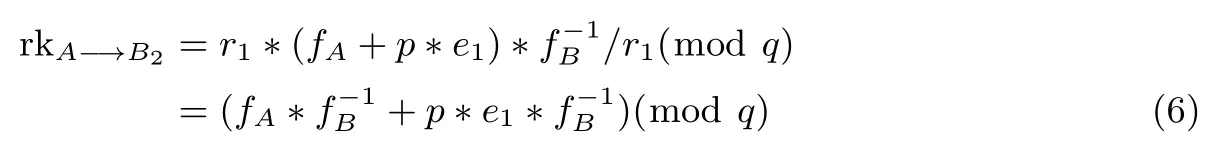
• 加密(Encrypt):该算法的输入是授权者A的公钥pkA和需要加密的明文m.该算法的过程是首先由Ř中随机选取多项式r2,计算密文CA=pkA∗r2+m(modq),最终输出密文CA.

• 重加密(ReEnc):该算法的输入是密文CA和重加密密钥rkA−→B.该算法的加密过程是CB=rkA−→B2∗CA(modq)由于 pkA=p∗gA∗(modq),故得到最终密文

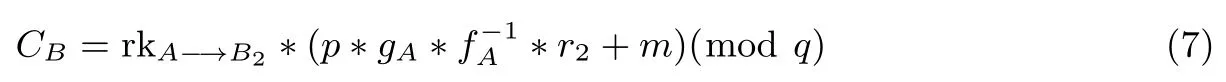
• 解密(Decrypt):该算法的输入是密文CB和被授权者的私钥skB.该算法的解密过程是

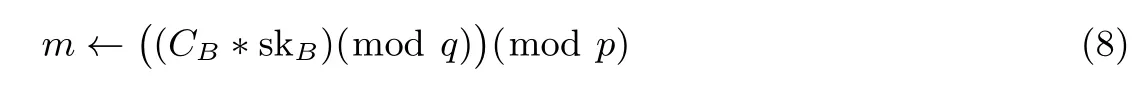
4 方案分析

在本节中,我们分析所提出方案的正确性、安全性、多跳性和单向性.

4.1 正确性分析

方案的正确性验证从两个方面证明:

(1)授权者A从密文CA成功恢复出明文,即计算:

随后对上式的最终结果进行模p运算:

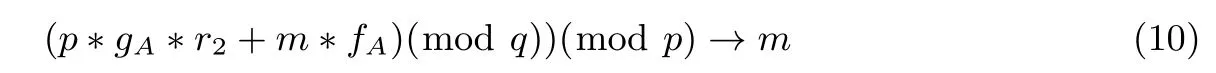
由于fA(modp)≡1(modp),所以最终可以恢复出原明文m.

(2)被授权者B收到云代理服务器的重加密后密文CB后,计算:

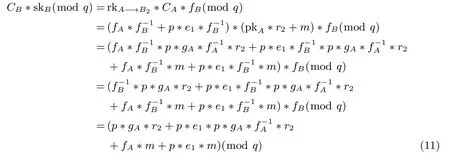
随后对上式的最终结果进行模p运算,得到:

在谈及新能源混合动力汽车之前，先了解一下传统意义技术层面上对混合动力汽车的定义—混合动力汽车也被称为复合动力汽车，其动力输出部分或全部依靠车载的内燃机提供，并根据对其他动力源(如电动源)的依赖程度分为弱混、轻混、中混和重混(全混)，根据其动力输出的分配方式分为并联、串联和混联。

因为fA≡1(modp),所以最终可以得出原明文m.提出的方案满足正确性要求.

4.2 安全性

本文方案是建立在NTRU方案的基础上,其安全性也等同于NTRU的安全性,由于NTRU密码体制缺乏形式化的安全性证明,因此本文通过几种攻击方式来验证方案的安全性.

针对私钥的攻击:通过此攻击方式,攻击者试图找到秘钥或可用于解密的密钥的替代密钥.假设在多项式时间内,攻击者可以很容易得到这样一对多项式 (f′,g′),使其满足g′=f′∗fq∗g(modq),那么该攻击者可以破解私钥.而该问题等价于最短向量问题(SVP),而SVP问题是一个多项式时间的NP困难问题,显然在多项式时间内,攻击者不可能破解求出私钥.

抵抗合谋攻击:在原方案重加密密钥格式为 rkA−→B=fA∗(modq),不能抵抗合谋攻击.在本方案中,我们改进了重加密密钥的生成算法,即 rkA−→B2=fA∗+p∗e1∗(modq),如果代理者C要与授权者A或被授权者B合谋获得被授权者B或授权者A的私钥,可由下列引理证明实现该种攻击不存在.

引理1对比原方案,本方案代理者C与授权者A不能合谋获得被授权者B的私钥.

证明:在原方案中,代理者C用自己的重加密密钥rkA−→B与授权者A的私钥fA作计算:

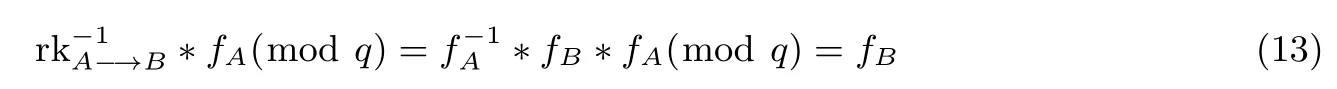
可以得到被授权者的私钥fB,即原方案不能抵抗代理者C和授权者A的合谋攻击.

本方案中,代理者C拥有重加密密钥 rkA−→B,首先是求重加密密钥rkA−→B的乘法逆元,由其结构可以看出,显然不能得到一个有效的逆元,或者是使用重加密密钥rkA−→B与授权者A的私钥fA的逆作计算:

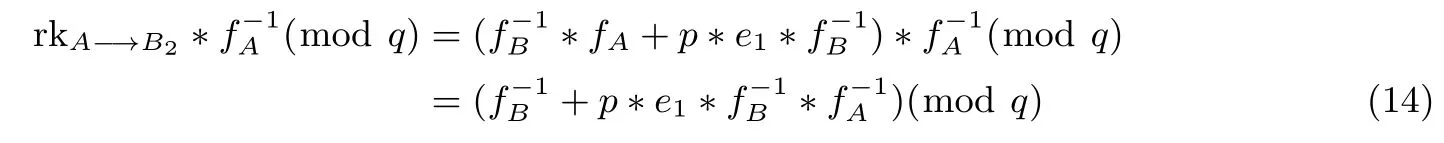
引理2本方案代理者C与被授权者B不能合谋获得授权者A的私钥.

证明:在原方案中,代理者C用自己的重加密密钥rkA−→B与被授权者B的私钥fB作计算:

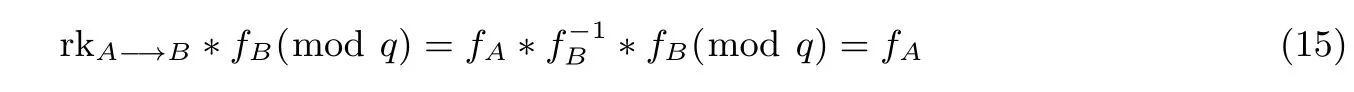
可以获得授权者A的私钥fA,即原方案不能抵抗代理者C和被授权者B的合谋攻击.

本方案中,由引理1知重加密密钥rkA−→B没有一个有效的逆元,因此与被授权者B的私钥fB作计算:

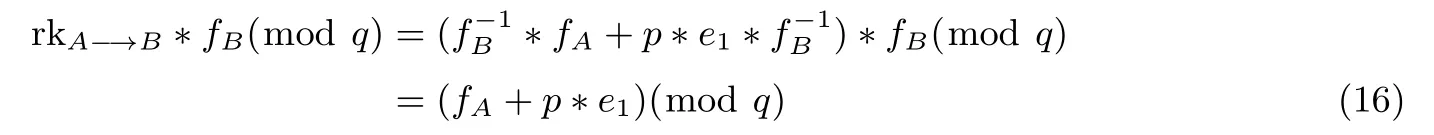
显然,由于随机多项式p∗e1的存在,两者合谋不能得到授权者A的私钥.

在原方案中,代理者C既能与授权者A合谋获取被授权者B的私钥,又能与被授权者B合谋获取授权者A的私钥.而本方案通过改进重加密密钥生成算法,使得该方案中的代理者C不能与授权者A或被授权者B合谋获得被授权者B或授权者A的私钥信息.

4.3 方案多跳性

代理者执行第一次重加密:

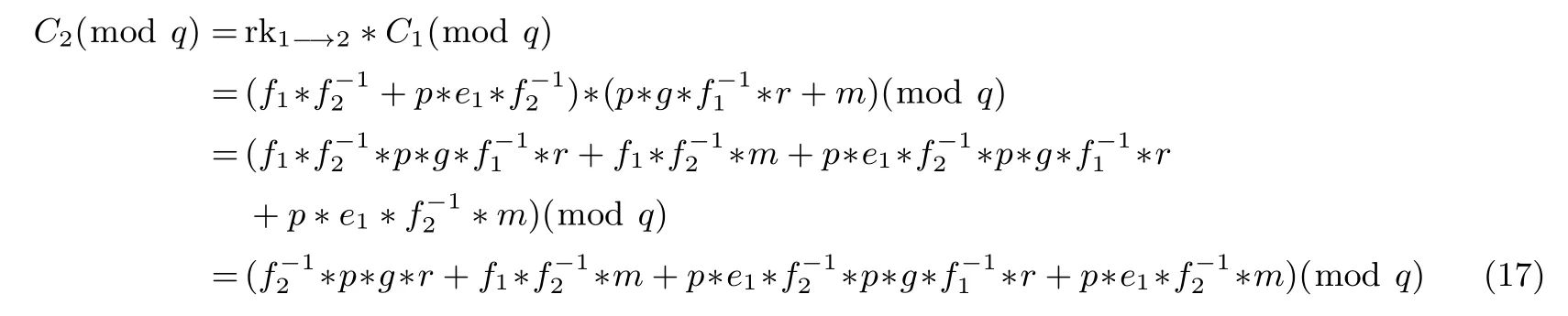
代理者执行第二次重加密:

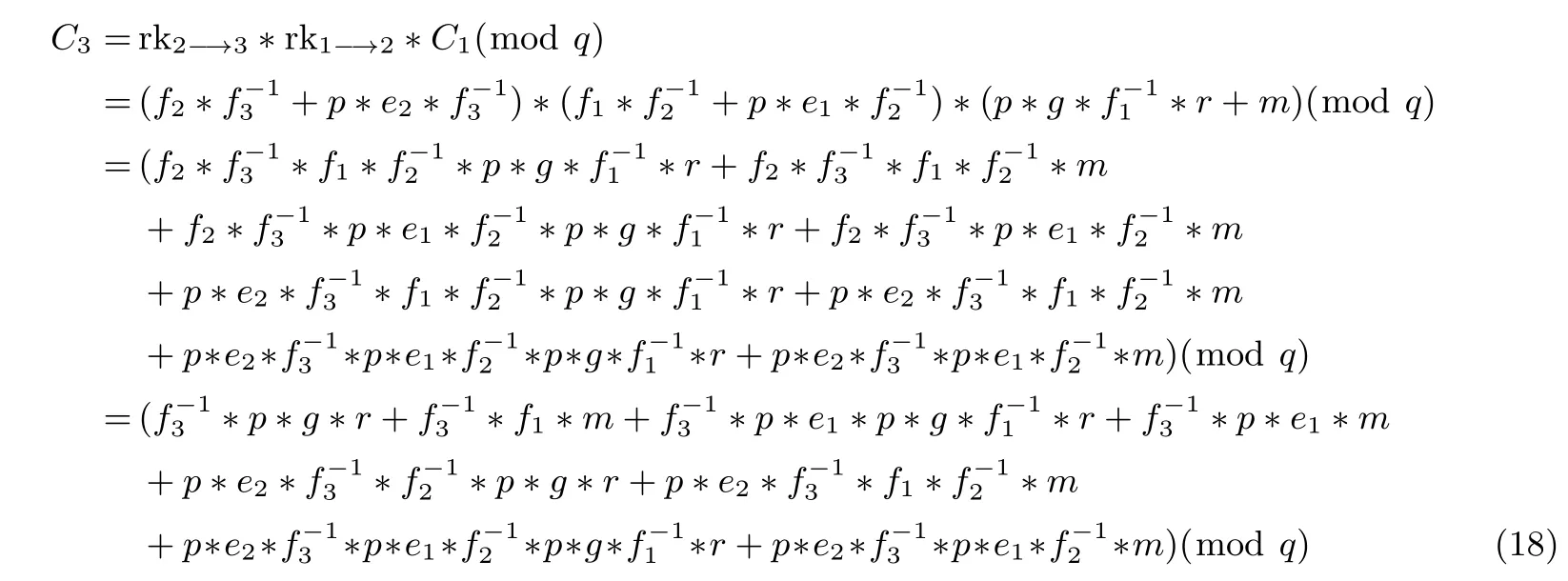
代理者执行第N−1次重加密:

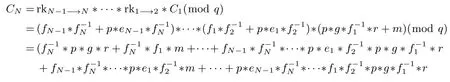
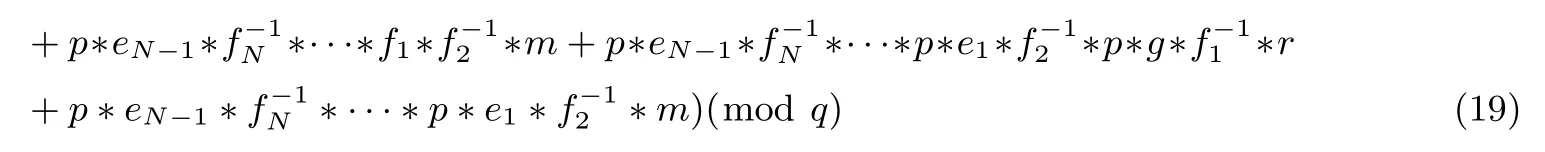
第N位接收者收到经过N−1次重加密后的密文CN后,先对密文执行解密运算,得到:

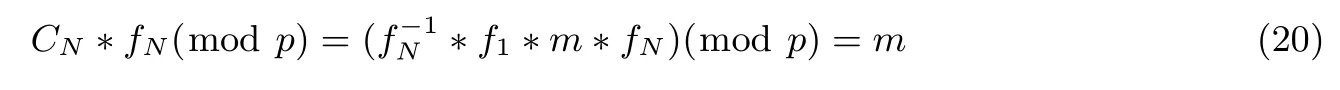
经上述验证,本方案在经过N−1次重加密后,最终仍能恢复出明文消息,本方案满足多跳性.

4.4 单向性

在原方案中云服务器C与授权者A、被授权者B通过重加密密钥生成协议生成重加密密钥rkA−→B=fA∗(modq),此时 rkA−→B可以将授权者A的公钥加密的密文转换成由被授权者B的私钥解密的重加密密文.但该方案的重加密密钥是可以由云服务器C通过对重加密密钥进行逆变换,生成一个新的重加密密钥可将被授权者B的公钥加密的数据转换成由授权者A的私钥解密的重加密密文,因此原方案是双向重加密方案.