SPECK型算法的积分分析和不可能差分分析*
2020-05-09方玉颖
方玉颖,徐 洪,2
1.数学工程与先进计算国家重点实验室,郑州450001
2.信息工程大学,郑州450001
1 引言
不可能差分分析和积分分析是分组密码两类重要的分析方法.不可能差分分析是差分分析方法的变形,由Knudsen和Biham[1,2]分别独立提出,其核心思想是利用分组密码不可能出现的特定输入输出差分排除错误密钥.不可能差分分析方法的关键是不可能差分特征的构造,中间相错是最主要的构造方法.积分分析由Knudsen等[3]在Square攻击、Saturation攻击和Multiset攻击基础之上提出,其核心思想是通过选择特定输入明文集,分析经多轮加密后某些比特是否具有特定的积分性质,比如平衡性,即对应的状态集求和为0的情形,再根据这些积分性质排除错误密钥.
积分攻击的关键是寻找长的积分区分器,对于分组规模较大轮函数较复杂的算法寻找其积分区分器通常是比较困难的.2015年欧密会上,日本学者 Todo[4]在传统积分的基础上提出了可分性 (Division Property)的概念,并成功刻画了可分性经过异或,复制,S盒等基本运算的扩散规律,实现了对分组算法积分区分器的有效搜索.同年美密会,Todo[5]利用可分性的思想,结合 S盒自身的缺陷,成功构造了MISTY1算法的 6轮积分区分器,首次实现了对 MISTY1算法理论上的全轮攻击.FSE 2016会议上,Todo和Morii[6]在已有工作的基础上,进一步给出了比特可分性(Bit-based Division Property)的定义,实现了对SIMON算法的积分区分器搜索.同年亚密会上,Xiang[7]等人将混合整数线性规划(MILP)思想应用到积分区分器的搜索中,先将分组密码比特可分性的传播过程转化为相应的MILP模型,再调用开源求解器Gurobi求解相应的MILP问题,最终实现了包括SIMON 128在内的多个分组密码算法积分区分器的自动化搜索.Wang和Sun[8–10]等人进而研究了ARX型分组密码的积分区分器的自动化搜索技术,通过刻画模加运算比特可分性的传播规律,建立了相应的MILP模型并实现了对HIGHT、TEA等多个分组算法积分区分器的搜索.
2013年,美国国家安全局 (简称 NSA)设计提出了两类重要的 ARX型轻量分组密码算法 SIMON和SPECK[11],其中SPECK算法整体采用变形的Feistel结构,算法轮函数由循环移位、模加和异或三部分组成.同时为了支持不同程度的信息安全,算法根据不同的分组长度和密钥长度提供了多个版本,相应的算法迭代轮数也有所不同.目前对SPECK算法主要的攻击方法包括差分分析,线性分析,积分分析,零相关线性分析和不可能差分分析等[12–21].
作为轮函数中主要的线性扩散层,不同移位参数对应的 SPECK算法的安全强度一般也不同.2016年FSE会议上,Biryukov等[17]在研究SPECK算法最优差分路径的搜索问题时,列出了分组长度为32,48,64比特的SPECK型算法的部分差分最优移位参数.本文在此基础上针对不同分组长度,进一步分析了不同移位参数对应的SPECK型算法的积分性质和不可能差分性质,完善了对SPECK型算法安全性能的分析.
本文主要安排如下:第2节给出了文中要用到的一些符号,并简要介绍了SPECK算法.第3节利用混合整数线性规划方法,基于可分性搜索了SPECK型算法的积分区分器,并给出了不同移位参数对应的积分区分器的轮数.第4节利用中间相错思想和模加差分的性质搜索了SPECK型算法的不可能差分特征,并给出了不同移位参数对应的不可能差分特征的轮数.第5节为简单的小结,结合已有差分分析的结果,给出了能综合抵抗多种攻击的优化移位参数.
2 预备知识
2.1 符号说明
Lr: 第r轮左边的输入Rr: 第r轮右边的输入
kr: 第r轮的轮子密钥⊕: 异或
∧: 按位与 +: 模2n加法
≪α:循环左移α比特 ≫β:循环右移β比特
:F2上n维向量空间a:F2上n维向量
a[i]: 向量a∈的第i个比特w(a):向量a∈的汉明重量
W(a):向量a=(a0,···,am−1)∈×···×的向量汉明重量,W(a)=(w(a0),···,w(am−1))
2.2 SPECK算法简介
SPECK系列算法[11]采用变形的Feistel结构,轮函数由循环移位、模整数加法和异或运算组成,主要的非线性部件为模整数加法,具体结构如图1所示.

图1 SPECK算法的轮函数Figure 1 Round function of SPECK
设 SPECK 算法第r−1轮的输入为 (Lr−1,Rr−1),输出为 (Lr,Rr),轮子密钥为kr−1,移位参数记为 (α,β),则经过一轮迭代后的输出为
Lr=(Lr−1>>>α)+Rr−1⊕kr−1
Rr=(Lr−1>>>α)+Rr−1⊕(Rr−1<<<β)⊕kr−1
以下简记移位参数为 (α,β)的 SPECK 算法为 SPECK(α,β)算法. 原 SPECK32算法的移位参数(α,β)=(7,2),更长分组的 SPECK 算法的移位参数 (α,β)=(8,3).
2016年FSE会议上,Biryukov等[17]在研究SPECK算法最优差分路径和线性路径的搜索问题时,给出了不同移位参数下SPECK型算法的最优差分路径对应的最大差分概率.在考虑减轮版本SPECK型算法的安全性时,他们发现在固定移位参数的情形下,移位参数(9,2)比原始参数(7,2)对应的SPECK算法具有更好的差分性质,移位参数(4,3)、(5,3)、(7,3)、(13,3)的SPECK48算法比原始参数(8,3)对应的差分性质更好,而移位参数 (2,3)、(4,3)、(5,3)、(7,3)、(9,3)、(10,3)、(11,3)、(12,3)、(15,3)的 SPECK64算法和原始参数(8,3)对应的差分性质相当,均达到最优.本文将在此基础上进一步研究不同移位参数的SPECK型算法的积分性质和不可能差分性质.

3 SPECK型算法的积分分析
本节先简要回顾可分性的概念和可分性的传播规律,建立相应的MILP模型,再给出SPECK型算法积分区分器自动化搜索的步骤和结果.
3.1 可分性
可分性的概念由日本学者Todo[4]在2015年欧密会上提出,之后Todo,Xiang,Sun[6–10]等人又相继研究了基于比特的可分性质,分析了可分性在基本运算上的扩散规律,并利用MILP,SAT等方法实现了多个分组算法积分区分器的搜索.下面简要介绍可分性的定义以及一些基本运算的可分性传播规律.
比特可分性经过一些基本运算,如复制(COPY)、异或(XOR)、按位与(AND)的传播规律如下:
性质 1(复制)[6,7]设F是复制运算,输入x∈F2,输出可表示为(y0,y1)=(x,x).令X和Y分别为对应的输入和输出集合,设X满足可分性,Y满足可分性,则传播过程如下所示

注:设多重集X具有可分性,则集合X没有积分性质当且仅当K包含所有单位向量.
根据上面的分析,寻找分组算法的积分区分器时,可以从仅含一个非活跃比特(块)的输入集出发,分析经轮函数迭代后可分性的传播规律.若r轮迭代后输出集对应的可分性K中首次包含所有单位向量,则存在相应的(r−1)轮积分区分器.
3.2 MILP模型
Xiang等人在文献[7]中利用混合整数线性规划(MILP)思想,将分组密码可分性的传播过程转化为不等式表示,并调用开源求解器Gurobi求解相应MILP模型,实现了对多个轻量分组算法积分区分器的自动化搜索.Sun等人[8,9]进一步刻画了模加运算可分性传播的 MILP模型,实现了对一般ARX型分组密码的积分区分器的搜索.他们建立的基于比特的复制、异或和与运算的MILP模型如下:
模型 1(复制)[8]设复制运算的比特可分性为(a)(b0,b1,···,bm),则有
模型 2(异或)[8]设异或运算的比特可分性为 (a0,a1,···,am)(b),则有

模型 3(按位与)[8]设按位与运算的比特可分性为(a0,a1)(b),则有
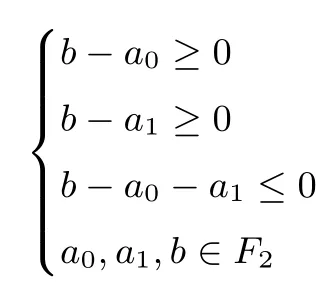
对于模加运算,Sun等[8,9]首先通过引入进位变量,给出了模加运算各分量的代数标准型.不妨设输入和输出分别为x=(x0,x1,···,xn−1),y=(y0,y1,···,yn−1),z=(z0,z1,···,zn−1),满足z=x+y,则各分量间满足如下关系

根据上式给出的各分量间的函数关系,可以将模加运算转化为复制、异或、按位与等基本运算的复合,再结合模型1–3即可给出其可分性传播的MILP形式.不妨以n比特数的模加运算为例,其可分性传播的MILP模型可以如下构造,各中间变量的分配表如表1所示.
设n比特模加运算输入输出可分性分别记为 (b0,b1,···,bn−1)、(d0,d1,···,dn−1) 和 (e0,e1,···,en−1),中间变量如上表所示,则模加运算可分性的传播 (b0,b1,···,bn−1)+(d0,d1,···,dn−1)(e0,e1,···,en−1)可表示为如下形式


初始可分性和终止条件[7]记为一条 (r+1)轮可分路径,L为刻画该(r+1)轮算法可分性传播规律的不等式形式.设算法的输入和输出可分性分别为,其中K0={k}={(k0,k1,···,k2n−1)}.为了构造 (r+1)轮算法完整的 MILP 模型,我们首先需要对算法的初始可分性进行赋值,即将等式=ki(i=0,1,···,2n−1)作为约束条件添加到不等式组L中;其次,根据3.1节的说明,易知当输出集的可分性中包含所有的单位向量,即说明此时集合不存在可分性,因此我们将目标函数设置为即第r+1轮输出状态集可分性各分量的求和.在调用开源求解器Gurobi求解后,若存在2n种输出变量使得目标函数取值为1,即说明集合Kr+1包含所有2n个单位向量,则由可以得到一条r轮积分区分器.

表1 n比特模加中间变量分配Table 1 Allocation of intermediate variables for n-bit modular
3.3 积分区分器搜索
对于分组长度为2n比特的SPECK型算法,基于比特可分性,利用MILP方法自动化搜索积分区分器的具体流程如下:
步骤 1:选择仅含一个非活跃比特的特定的输入集 (A,···,C,···,A)相应的比特可分性为其中C表示常量比特,A表示活跃比特,常量比特所在位置可以是任意的i∈{0,1,···,2n−1};
步骤 2:根据 3.2节中给出的 SPECK(α,β)算法的单轮可分性传播模型,构造完整 (r+1)轮SPECK(α,β)算法积分区分器搜索的MILP模型,并设置目标函数为
步骤3:调用开源求解器Gurobi求解MILP模型.若输出集可分性中集合Kr+1包含所有2n个单位向量,则算法终止,由可以返回一条r轮积分区分器;
步骤4:若集合Kr+1不包含所有2n个单位向量,则继续迭代1轮,重复步骤2和步骤3,直到程序返回一条有效的积分区分器.

图2 SPECK32算法1轮差分路径Figure 2 1-round of differential trail of SPECK32 algorithm
根据上述步骤,基于MILP方法我们对采用不同移位参数(α,β)的SPECK型算法的积分区分器进行了搜索.对于不同分组长度的 SPECK型算法,固定β为原算法的移位参数,当移位参数α变化时,表2列出了不同参数下能够找到的积分区分器的轮数.

表2 SPECK型算法积分区分器的轮数(32/48/64比特分组)Table 2 Round of integral distinguishers of SPECK-like algorithm(32/48/64-bits block)
从表中数据可以看出,在减轮情形下,当固定β=2时,移位参数为(8,2),(9,2),(10,2)的SPECK32算法对应的积分区分器的轮数比用原始参数(7,2)时少一轮,具有更强的抵抗积分分析的能力.同样对于SPECK48算法,固定β=3时,移位参数为(11,3),(12,3),(13,3),(14,3),(15,3),(16,3)的 SPECK算法比原算法具有更强的抵抗积分分析的能力.而对于SPECK64算法,移位参数为(15,3),(16,3),(17,3),(18,3),(19,3),(20,3)的SPECK算法比原算法具有更强的抵抗积分分析的能力.
4 SPECK型算法的不可能差分分析
本节将利用中间相错方法给出对SPECK型算法不可能差分分析的结果.文献[21]刻画了如下模加运算的差分扩散性质.
引理 1[21]设模加运算记为z=f(x,y)=x+ymod 2n,不妨设向量a=(a0,···,an−1),b=(b0,···,bn−1)为输入差分,向量c=(c0,···,cn−1)为相应的输出差分. 另外记la=max{k|ak=1,ak+1=···=an−1=0},lb=max{k|bk=0,bk+1=···=bn−1=0},则有如下性质:
(1)若la=lb=l,则cl=···=cn−1=0,且对于 0≤i (2)若la̸=lb,设l=max(la,lb),则cl=1,cl+1=···=cn−1=0,且对于 0≤i 对于 SPECK 32算法,我们发现若该算法存在某r轮不可能差分特征,其输出差分形如(00···0 10···0), 则可以自然拓展一轮, 得到输出差分形如 (10···0 10···10) 的 (r+1) 轮不可能差分特征(参见图2).采用大分组和其它移位参数(α,β)的SPECK型算法也有类似的性质.下面重点关注不同移位参数对应的这类不可能差分特征的轮数. 根据上面的分析,对于SPECK(α,β)算法,为了节约搜索时间,我们在搜索SPECK型算法的不可能差分特征时,限定输入差分为单位向量,即满足且输出差分∆Output0=(v0,···,v2n−1)满足v0=vn=v2n−β=1,其余位置为 0.具体搜索流程如下: 步骤1:对选定的输入差分∆Input0进行加密,若第rin+1轮的输出差分满足所有位置取值均不确定,则记rin为加密最大轮数; 步骤2:类似步骤1的方法,对于选定的输出差分∆Output0同样可以得到解密最大轮数,记为rout,同时记rtotal=rin+rout; 步骤3:对满足r1+r2=rtotal的所有组合(r1,r2),判断中间状态的差分∆Inputr1和∆Outputr2是否存在某些位置比特相互矛盾,若存在则返回一条rtotal轮的不可能差分特征,否则rtotal=rtotal−1并重复步骤3; 步骤4:对所有的重复步骤1–3. 根据上述步骤,我们对采用不同移位参数(α,β)的SPECK型算法的不可能差分特征进行了搜索.对于不同分组长度的SPECK型算法,固定β为原算法的移位参数,当移位参数α变化时,表3列出了不同参数下能够找到的不可能差分特征的轮数. 表3 SPECK型算法的不可能差分特征的轮数(32/48/64比特分组)Table 3 Round of impossible differentials of SPECK-like algorithm(32/48/64-bit block) 从表中数据可以看出,在减轮情形下,当固定β=2,移位参数为 (2,2),(3,2),(4,2),(9,2),(10,2),(11,2)的 SPECK 32算法的不可能差分特征的轮数比选用原始参数 (7,2)时少一轮,具有更强的抵抗不可能差分分析的能力.同样对于 SPECK 48算法,当固定β=3时,移位参数为 (3,3),(4,3),(5,3),(6,3),(14,3),(15,3),(16,3)的 SPECK算法比原算法具有更强的抵抗不可能差分分析的能力.而对于SPECK 64算法,移位参数为 (3,3),(4,3),(5,3),(6,3),(18,3),(19,3),(20,3)的 SPECK算法比原算法具有更强的抵抗不可能差分分析的能力. 本文分析了当移位参数变化时,不同分组长度的 SPECK型算法抵抗积分分析和不可能差分分析的能力.基于MILP方法和中间相错方法,我们给出了不同移位参数对应的SPECK算法的积分区分器和不可能差分特征的轮数.结合Biryukov等[17]关于SPECK型算法差分分析的结论,我们发现当考虑减轮版本的SPECK型算法的安全性能时,采用移位参数 (9,2)的 SPECK32算法比原始算法具有更强的抵抗差分分析、积分分析和不可能差分分析的能力.当分组长度为48比特时,与原始参数(8,3)相比,采用移位参数(4,3)和(5,3)的SPECK算法在抵抗差分分析和不可能差分分析时有着较好的优势,而采用移位参数(13,3)的SPECK算法在抵抗差分分析和积分分析上的表现更好.当分组长度为64比特时,采用移位参数 (18,3),(19,3),(20,3)的 SPECK算法比原始算法具有更好的抵抗积分分析和不可能差分分析能力,而采用移位参数(4,3),(5,3)的SPECK算法具有更好的抵抗差分分析和不可能差分分析能力,采用移位参数(15,3)的SPECK算法具有更好的抵抗差分分析和积分分析能力.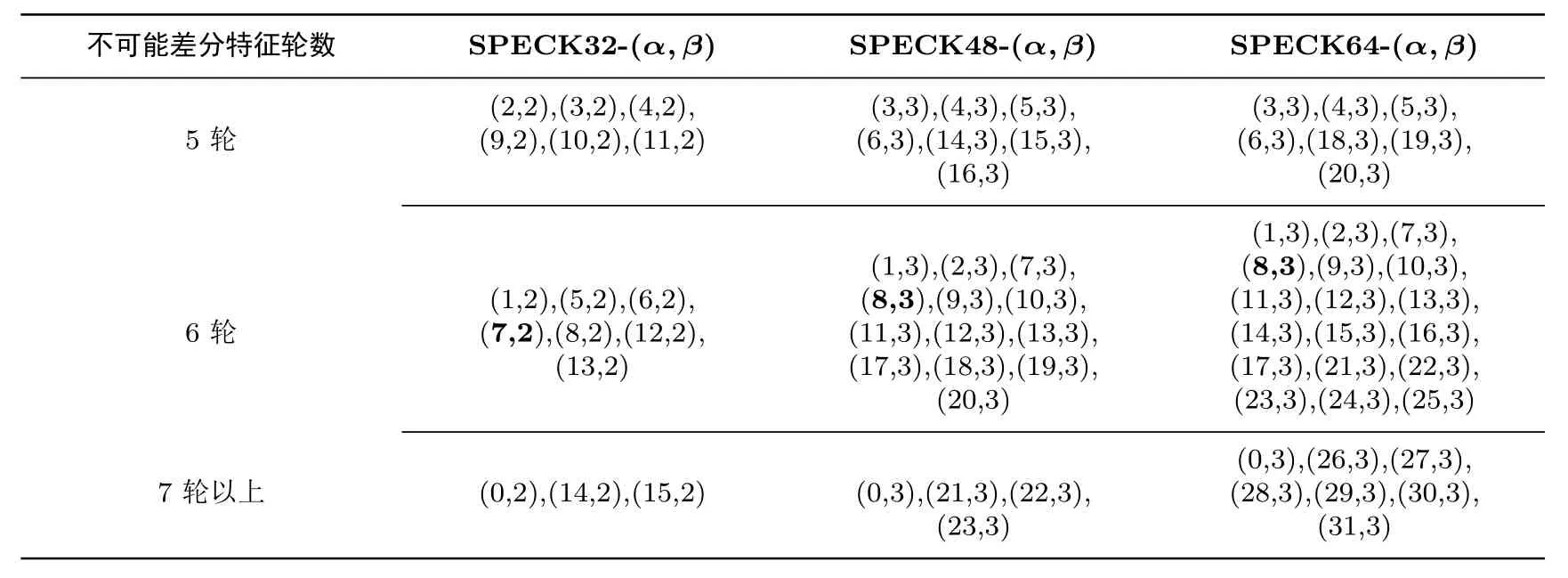
5 总结
