一种结合时间因子聚类的群组兴趣点推荐模型

陶永才,曹朝阳,石 磊,卫 琳

1(郑州大学 信息工程学院,郑州 450001)2(郑州大学 软件技术学院,郑州 450002)

1 引 言

近年来,由于个人电脑和网络的普及,大量用户和用户信息涌入互联网.在用户向互联网不断提供信息、文件、多媒体资源的同时,也在不断的从互联网中查询和获得各种需要的信息和资源.因此推荐系统伴随各种应用快速发展.

作为数据过滤工具的一种,推荐系统通过挖掘、整理、分析用户在网站上的行为轨迹和数据,并对这些数据进行建模,从而得到用户隐式的需求和兴趣信息.

现存经典推荐系统通常倾向于为单个用户进行推荐.而随着移动设备的普及和各种社交网络的app的出现,传统的线下集体活动开始逐渐转变为以网络为媒体的线上群组活动,如去餐厅就餐,度假旅游,家庭娱乐视频等.因此,推荐系统需要以群组为单位,综合考虑群组中用户权重与偏好,生成群组推荐.由此组推荐系统(group recommender system)产生.

本文提出一个基于时间因子聚类的群组兴趣点推荐模型(A Group POI Recommendation Model Based on Time Factor Clustering,AGRT),考虑到用户在一天当中不同时间点的不同兴趣点偏好,并结合隐语义推荐模型对群组兴趣点进行推荐,较好的克服了用户数据稀疏性问题.

2 相关工作

目前主流的组推荐系统推荐策略通常使用协同过滤推荐(collaborative filtering,简称CF)向组用户产生推荐.这些策略通常可以分为两类:基于内存的协同过滤推荐(memory-based CF)和基于模型的协同过滤推荐(model-based CF).其中,基于内存的协同过滤推荐按照融合策略的不同又分为基于个人模型的融合策略(aggregating individual model,AIM)和基于个人预测融合策略(aggregating individual prediction,AIP).基于个人模型的融合策略首先融合群组成员的偏好为组偏好然后利用传统个人推荐算法进行推荐;而基于个人预测的融合策略首先为每个群组成员生成个人推荐,然后融合这些个人推荐列表生成组推荐[1].

Wang,Liu等人梳理了传统个性化推荐系统的概念以及传统推荐系统的各个模块以及各个模块常用的建模方法,传统推荐算法种类以及推荐系统评价标准[12].Zhang,Du等人引入了组推荐系统的概念,详细比较了组推荐系统与传统推荐系统的不同,并介绍了组推荐系统的各个环节所用的技术,偏好融合策略、群组特征对偏好融合策略的影响以及组推荐系统评价标准[14].文献[2]基于组用户易受群组中专家成员意见影响的趋向提出了一种基于注意力机制的组推荐模型(AGR),利用该模型学习群组中专家成员对其他成员影响并能够针对不同的领域推荐调整模型.

当前个性化推荐的研究热点主要集中于群组、兴趣点推荐[3-11].组推荐系统研究的主要问题之一是如何在现有融合策略中进行选择以及如何对选择后的融合策略根据用户模型特点进行改进.偏好融合方法的选择需要考虑群组类型、群组规模以及具体的推荐算法等因素.模型融合则不能忽视评分稀疏性的影响,评分少的群组成员在一般模型融合时对群组偏好模型的影响也较小,就产生了模型融合中所谓的不公平问题.推荐融合方法则没有将群组成员之间的相互影响考虑在内.组内相似度也对融合方法有着不可忽略的影响,文献[14]提出大部分的模型融合方法和推荐融合方法的准确度与组内相似度存在正相关关系.

3 结合时间因子的群组兴趣点推荐模型

群组用户对兴趣点的选择受到各种因素的影响,其中无法忽视的影响之一就是用户一天当中所处的时间点,在不同的时间点用户所感兴趣的地点也不相同.因此本文提出的AGRT模型结合K-menas聚类算法,对用户签到地点以时间轨迹进行聚类,结合当前时间生成群组数据集,通过LFM隐语义算法计算出个人推荐列表,然后对结果使用加权混合融合策略,最终产生群组推荐.

AGRT模型推荐过程如图 1所示.

①获取数据,对用户数据集用K-means算法进行聚类；

②根据当前时间整理出群组成员User-item矩阵,用LFM隐语义模型生成组成员个人推荐列表；

③根据群组分歧度和群组成员权重,选用合适的加权算法,生成组推荐列表,将组推荐列表的首个推荐推荐给该群组.

3.1 个人推荐列表

3.1.1 K-means算法

作为一种启发式迭代聚类算法,K-means算法的主要思想是以距离作为度量指标,将样本集划分为若干个簇.K-means聚类的目标是簇内样本点间距离尽可能小,簇间距离尽可能大.如果选取欧式距离作为相似度指标,该算法最小化公式如式(1)所示.

(1)

在本文中,对用户数据集使用K-Means算法,步骤如下:

1)从数据集中选取k个样本,以其为初始簇心(以签到时间点为选择依据,采用随机选取方式):{μ1,μ2,…,μk}；

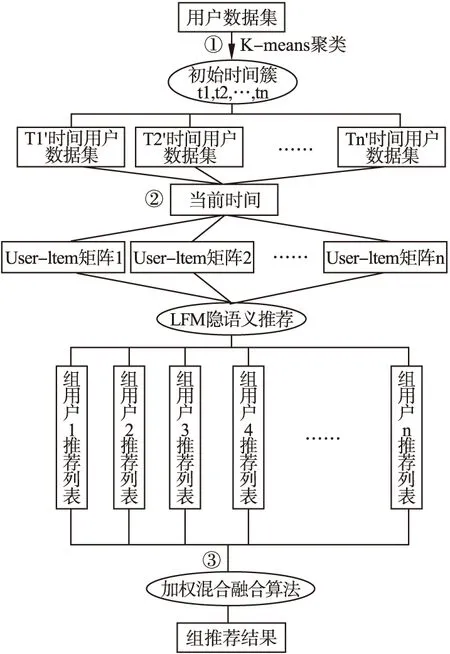
图1 AGRT推荐流程Fig.1 Recommended flow

2)计算每个样本点与簇心之间的距离,将其划分到距离最短的簇心所在类;

3)更新簇心:对每簇中的所有样本签到时间求平均,以该平均作为该类的簇心;计算最小化公式的值;

4)看簇心和最小化函数值是否变化;若不变,则输出聚类结果;若改变则返回2).

图 2 展示了当聚簇个数k=8本文数据集的聚类结果,图 3和图 4展示了不同簇在相同签到兴趣点的频数差异,图2(a)～图2(h)中横坐标为签到兴趣点(随机选取和签到频数最高前14个),纵坐标为用户在该地点的签到频数.从图2中可以看出在不同时间点为簇中心点的用户签到数据有明显差异,也证实了时间因子对用户选择兴趣点确实存在影响.

3.1.2 基于隐语义推荐(LFM)的推荐算法

推荐系统使用用户的已有行为数据预测用户可能行为或偏好行为,但现存推荐系统往往面临数据稀疏性和冷启动问题.使用隐语义模型能够某种程度的缓解协同过滤面临的问题,同时也为解决数据稀疏性和冷启动问题提供了一种新的思路[13].隐语义模型LFM和LSI,LDA,TopicModel都属于隐语义分析技术,他们的本质是找出待评价项目中潜在的主题或分类,这些主题或分类被理解为用户的兴趣属性.隐语义技术首先在文本挖掘领域提出,近年来被不断应用到其他领域,取得了显著的效果.

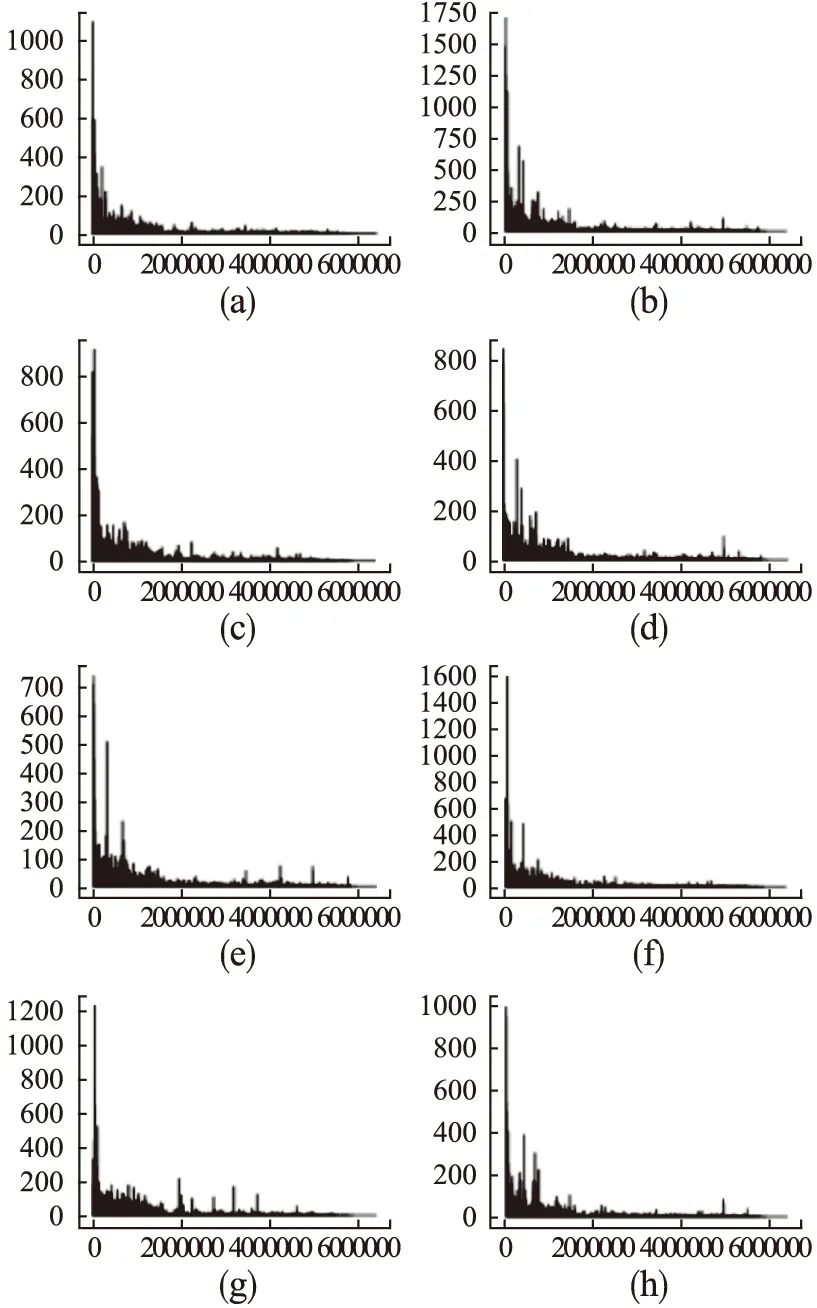
图2 类簇个数k=8时聚类结果图(图(a)(b)(c)(d)(e)(f)(g)(h)中纵坐标为用户签到点(兴趣点),纵坐标为签到频数)Fig.2 Clustering result graph with k=8

本文首先对用户签到数据进行建模,如公式(2)所示.

(2)

R矩阵就是user-item矩阵,矩阵值i∈(1,m)、j∈(1,n)表示的是第i个用户对第j个项目的兴趣度,通常可以通过显式获取和隐式获取两种方式得到用户偏好数据,显式获取需要用户对所有项目评分,隐式获取则使用用户的已存在行为数据来分析用户偏好.隐式获取不会用户产生干扰,并且能够尊重用户隐私.基于用户的签到信息只能获得用户的兴趣点和签到次数,显然本文只能采取隐式获取的方法,以用户在对应兴趣点的签到次数作为用户对该点的评分,如公式(3)所示.

(3)

其中sum(ui,pj)代表用户ui在点pj处的签到次数,若用户ui在点pj处无签到记录,则设评分为0.得到评分矩阵以后,LFM隐语义模型需要将Rmxn矩阵表示为两个矩阵P和Q的乘积,如公式(4)、公式(5)所示.

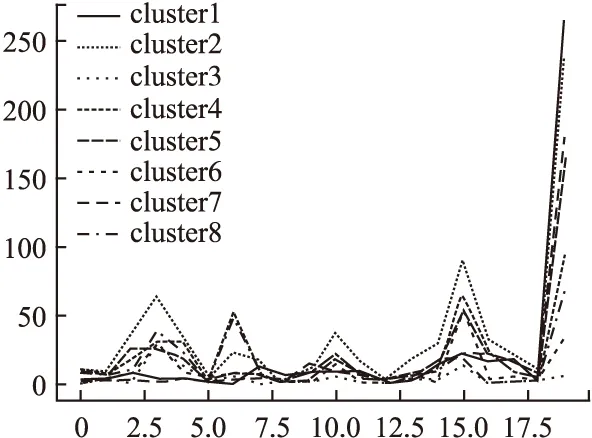
图3 签到频数对比图a(随机选取20个兴趣点)Fig.3 Check-in frequency contrast graph a (Random selection of 20 check-in point)

(4)

(5)

其中P矩阵为user-class矩阵,矩阵值pi,j为user i对class j的兴趣度;Q矩阵为class-item矩阵,矩阵值qi,j为item i在class j中的权重;因此LFM根据式(6)计算用户U对物品I的兴趣度.

(6)

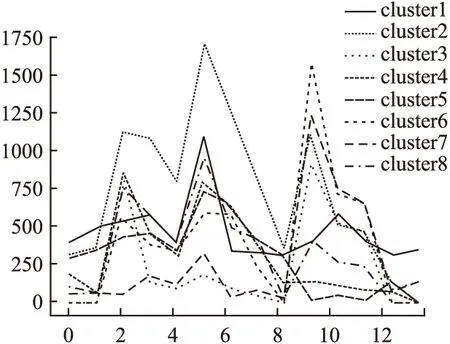
图4 签到频数对比图b(签到频数最高的14个点)Fig.4 Check-in frequency contrast graph b (14 points with the highest check-in frequency)

首先随机给定P矩阵和Q矩阵的初始值,然后通过随机梯度下降算法最小化损失函数使P·Q的值逼近R,损失函数如公式(7)所示.

(7)

损失函数右边部分的λ(‖Pi‖2+‖Qj‖2)项是L2正则化项,可以降低过拟合问题导致分解后的矩阵元素太大.

对上式通过求参数Pi和Qj的偏导确定最快的下降方向,如公式(8)、公式(9)所示.

(8)

(9)

通过迭代计算不断优化参数,直到参数收敛.迭代公式如公式(10)、公式(11)所示.

(10)

(11)

3.1.3 评分预测

综合3.1.1,3.1.2节提出的步骤,得到组内成员评分预测算法流程如算法1所示.

算法1.个人推荐算法

输入:matrix,用户-兴趣点签到矩阵;

G,待推荐用户集合;

N,计划推荐项目数;

Tcur,当前时间；

输出:每个组用户的个人推荐列表L={l1,l2,…,lm}.

1.foreach user uiin G

2.利用k-means算法聚类出用户在各个时间点签到类簇集合{u1t1,u1t2,…,u1tn},{u2t1,u2t2,…,u2tn},…,{umt1,umt2,…,umtn}

3.得到ti,其中ti∈(t1,t2,…,tn)且有|ti-Tcur| = min{|tj-Tcur|,tj∈(t1,t2,…,tn)};令类簇集合{u1ti,u2ti,…,umti}为当前推荐集合

4.整理集合,生成user-item矩阵

5.利用隐语义模型生成P,Q矩阵

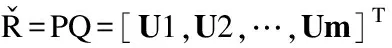
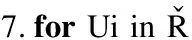
8.对Ui进行升序排序,选取得分最高的前N个项目推荐给用户

3.2 偏好融合策略

在生成群组个人推荐列表后,接下来需要选取合适的融合策略.为了尽可能的满足群组用户的满意度,以及对各个组员的公平性,推荐结果的可解释性,在实际中对于不同的组推荐系统需要根据实际情况选择融合策略.

融合策略多种多样,每种融合策略都尽可能的想要实现融合的平衡和满意.但现有融合策略均存在一定的优缺点和适用局限性,例如均值策略可能会引起部分群组成员的痛苦问题,最小痛苦策略可能会受到恶意评分的影响.表1对几种组推荐融合策略进行了说明.

表1 常用融合策略
Table 1 Aggregation strategy in common use

名 称解 释公平策略每次推荐轮流选取群组成员的评分作为群组评分均值策略计算所有群组成员评分的算术平均值作为群组评分痛苦避免策略选择痛苦阈值α,以高于痛苦阈值成员评分平均值作为群组评分最受尊敬者策略从群组成员中选择某个用户,将其评分作为群组评分最小痛苦策略选择所有群组成员中最低评分作为群组评分

考虑到群组中不同组成员签到次数的非均衡性或者用户的活跃度问题,也即少量用户拥有大量签到记录,而大量用户只有少量签到记录.显然签到次数越多的用户对群组偏好影响越大,因此本文采用加权混合融合策略对群组偏好进行融合,并采用以下模型计算用户权重,如式(12)所示.

(12)

其中G代表群组,I代表所有群组签到兴趣点集合,其中s(ui,pj)计算方法如式(13)所示.

(13)

采用加权混合融合策略,组推荐流程如算法(2)所示.

算法2.组推荐算法

输入:L={l1,l2,…,lm},群组成员个人推荐列表

G,组用户集合;

输出:组推荐结果.

1.foreach user uiin G

2. calculate weight w(ui)

3.endfor

4.foreach pain L

5.for(i in G)

6. GR[j] +=w(ui)·rat(ui,pa) //rat(ui,pa)计算见公式(3)

7.endfor

8.endfor

9.sort the GR[j] in descending order;

10.make the GR[0] as recommendation result

11.end

4 实 验

4.1 数据集

本文采用的数据集采集于斯坦福大学Gowalla网站,Gowalla网站是近年来非常热门的一个check-in签到网站,大量有关geo-tag和location-based的应用研究都可以在该数据集上开展.该数据集包含6442890个签到记录,数据集样本包含了兴趣点推荐所需要的全部信息.本文在实验前对数据进行整理,过滤掉了签到频数过低的用户.

4.2 算法评价标准

本文采用F值(准确率和召回率调和平均)为指标评价个人推荐列表.对任意用户u,Ru为算法推荐地点集合,Tu为测试集中用户u签到点集合,推荐准确率P、召回率R、以及F值公式分别如式(14),式(15),式(16)所示.

(14)

(15)

(16)

RMSE(平方根误差)把预测评分与真实评分之间的误差作为评价推荐系统的标准.本文对RMSE进行改进,使用改进后的公式对组推荐结果进行评价,如式(17)所示.

(17)

r(ui,pa)为用户ui对点pa的打分,r(G,pa)为组G对点pa的打分,|G|为组成员个数.

4.3 实验结果

4.3.1 隐语义模型K值比较

隐语义模型的分类数K的值代表对兴趣点的分类粒度,分类数越大则粒度越细,而分类数越小则粒度越粗.本文实验通过设置不同的K值对推荐结果进行评价,实验结果如图 5 所示.从图中可以看出当K=15,选取前20个推荐结果作为最终推荐结果时,获得了最高的F值,推荐效果较好.

图5 不同K值对个人推荐准确率的影响Fig.5 Precision of different values of K

4.3.2 加权混合融合策略和其他融合策略的比较

为了验证AGRT算法的有效性,本文通过实验,将本文提出的算法与几种现存算法就融合策略进行了比较,实验结果如图 6 所示.从实验中可以看出,AGRT算法较其他目前常用的几种算法有较明显的改进,并且AGRT在低相似度群组中的表现优于高相似度的改进.其中,该系统在低相似度(随机)群组和高相似度群组评测条件下下较HAaB提高了5.19%和2.06%.

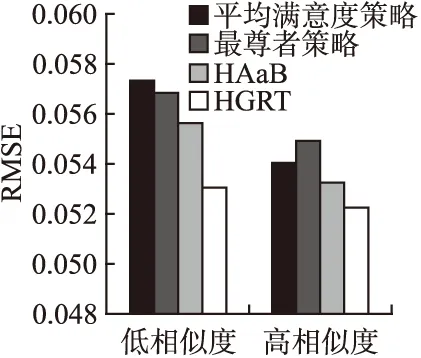
图6 不同融合策略实验数据对比Fig.6 Results comparison on aggregation strategies

5 总结与展望

本文提出了一种K-means时间因子聚类和隐语义模型相结合的群组兴趣点推荐算法,在实验数据集上取得了较传统协同过滤推荐策略和融合方法相结合的组推荐系统较为理想的推荐效果.但由于本文所采用的数据集的局限性,不能保证算法的普适性.本文下一步的工作是在更为广泛的数据集上进行实验和改善算法,希望能够取得更为完善和普适的算法.