一种加权距离连续K中心选址问题求解方法
2020-05-09黄书强江秀美范人胜
黄书强,江秀美,范人胜
1(暨南大学 理工学院光电工程系,广州 510632)2(广东省农村信用社联合社,广州 510000)
1 引 言
选址问题是运筹学中经典的一种决策问题,有着非常广泛的应用,主要研究如何选择设施的数目和确定最优位置从而为用户提供相应的服务,有着巨大的经济和社会意义.自1964年Hakimi提出了K中心选址问题[1]之后,许多学者加入到研究这个问题的队伍中,纷纷提出自己的解决办法并且有了较大的进展.K中心选址问题是指在网络平面上选定K个建立服务站的最优位置,也就是在全局范围内寻找使得所有需求点到最近服务站的最大距离值最小的部署方案.K中心选址问题是研究其他选址问题的基础,在工厂、仓库、加油站、物流中心等的部署中都有应用.将中心选址问题以选取服务站方式进行分类可分为:离散和连续两种中心选址问题.离散K中心选址问题是指在给定的网络节点上选取K个最优位置建立服务站,而连续K中心选址问题则是在整个网络平面上选取最优的部署方案.连续K中心选址问题相对于基于节点的离散K中心选址问题,其服务站部署位置的选取对于环境的适应性更强,并且选取位置更具有一般性,但是求解过程的复杂度也更大[2].
对于K中心选址问题,目前大多数研究都是以离散中心选址为主,对于离散K中心选址问题的研究相对比较成熟.文献[3]提出先求得最大距离,之后再求最大覆盖问题,得到离散K中心选址问题最优解的方法.Mladenovi等人[4]提出基于可变邻域搜索和两种禁忌搜索启发式算法来求解无三角不等式的离散K中心选址问题.文献[5]提出一个新的整数线性规划公式获得边界值,从而获得更优解.Ilhan[6]提出算法迭代方式分配所有客户端的最大距离值,从而解决整数可行性的问题.文献[7]在文献[6]的基础上进行改进并获得了更优解.文献[8]基于最小顶点覆盖,通过改进贪心算法得到选址问题的最优解.
对于连续K中心选址问题的研究,国外的研究较为丰富.Chen[9]提出了一种求解欧氏距离的minimax和minisum位置分配问题的新方法.该方法基于为目标函数提供可微分近似,对于大规模网络有较好的效果但是不适用于小规模网络.文献[10]提出了Slab划分方法有效的求解欧几里得K中心问题.Suzuki等人[11]提出了Voronoi图启发式方法,给出了方形最优解的上界,得到方形区域特殊情况的计算结果.Handler 等人[12]用松弛算法解决连续中心选址问题.本质上是选择要服务的n个点的子集.利用集合覆盖算法获取K个可将网络节点覆盖的覆盖圆,调整最大圆的半径得到最优解.文献[13]在文献[11]的基础上减少松弛算法迭代次数以及子问题的数目,使得算法具有更好的性能.文献[14]以需求最大化为目标,设计基于矩阵编码与小生境技术的非支配排序多目标遗传算法对定位-分配问题进行求解.文献[15,16]分别利用自适应学习能力启发式算法和近似鲁棒优化启发式算法,来解决连续空间最大欧式距离P中心问题.上述文献中都是以服务站到最远客户节点的欧式距离作为优化目标来对连续K中心问题进行研究,本文主要研究服务站到客户点的最大加权距离最小.
智能算法已成为解决组合优化问题的重要方法,如粒子群优化算法和差分进化算法作为经典的群智能随机优化算法,非常适合求解连续K中心选址问题.文献[17-19]分别利用改进的粒子群算法、遗传算法和差分进化算法求解跳数距离的几何K中心选址问题,取得较好效果.受上述方法思想启发,针对加权欧式距离的K中心连续选址问题,本文提出改进的模拟退火粒子群优化算法(SA-PSO)进行解决.
2 连续K中心选址问题的模型
本文采用了几何的方式,将连续中心选址问题转化为图论问题来进行研究.上文中提到连续K中心问题可在除节点外的整个网络平面内选择合适位置建造服务站.给定网络图G(V,E).其中V={v1,v2,…,vn},表示的是n个网络节点的集合,E表示网络中所有节点边的集合.如图1(a)所示,给定固定半径r,如果两个节点之间的距离d小于半径r,则称这两个节点为邻接节点,且这两节点之间有边相连.
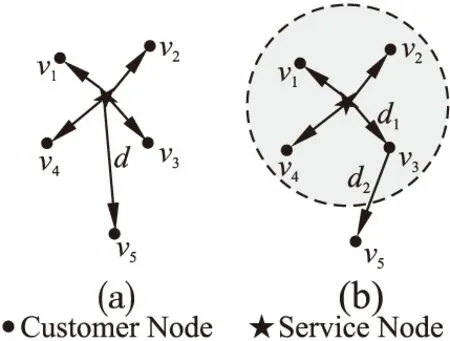
图1 连续K中心选址问题Fig.1 Continuous K-center location problem
如图1所示,d1表示的是客户点到部署服务站位置的最大欧式距离,d1+d2为最大加权距离.之前对于连续K中心问题是以d1作为其优化目标,也就是使得d1最小;本文考虑到实用性以及成本问题,主要以 服务站到客户点的最大加权距离作为优化目标,也就是求解使得d1+d2最小.

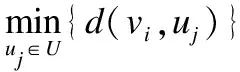
s.t.|U|=k
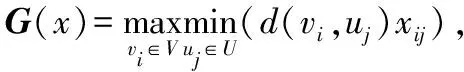
(1)
xij≤yj,1≤i≤n,1≤j≤n
(2)
(3)
xij,yj∈{0,1}, 1≤i≤n, 1≤j≤n
(4)
式(1)表明在网络范围内一个节点受且仅受一个服务站管辖;式(2)表示不是服务站的节点间关系是平等的,即节点i不会接受非服务站节点j的管制;式(3)表明总的有k个服务站,式(4)表明xij,yj都为二进制变量.
3 K中心选址问题的分类
离散K中心选址问题是指在给定的网络节点上选取K个服务站的最优位置,而连续K中心选址问题则是在整个网络平面上选取最优的部署方案.连续K中心选址问题相对于基于节点的K中心选址问题对于服务站部署位置的选取对环境的适应性更强,并且选取位置更具有一般性,但是求解过程的复杂度也更大.
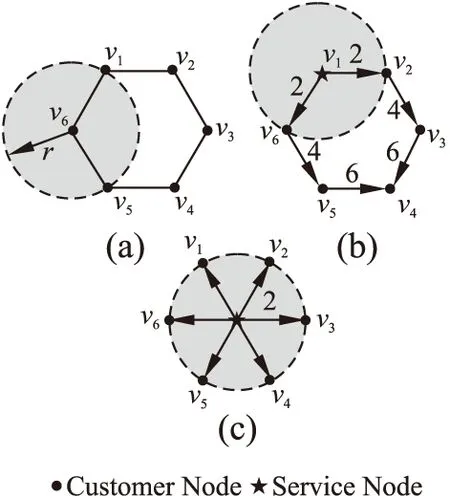
图2 6个客户节点服务站部署示意图Fig.2 Customer nodes service station deployment diagram
图2是以节点度为2的正六边形构成的6节点网络图,其构成了一个连通的闭环.六边形的边长为2,以一个固定半径的圆作为节点的最大覆盖范围.规定服务站到其他客户节点的距离用无向边上的权重表示.如图2(b)所示,根据离散K中心的方法选取服务站时,其覆盖半径为6;图2(c)中选取几何中心的位置设置服务站,将覆盖半径减少到2.
图3是由最邻近边距离为2的9个节点构成的网络图.服务站数目固定为2.以两种方式选取位置设置服务站,一是如图3(b)所示的服务站在已有的网络节点上选取,可得网络的覆盖半径为4;二是如图3(c)所示在网络平面的任意位置建立服务站,添加之前没有的10号节点,以2号与10号节点的位置建立服务站,网络的覆盖半径可降到2.
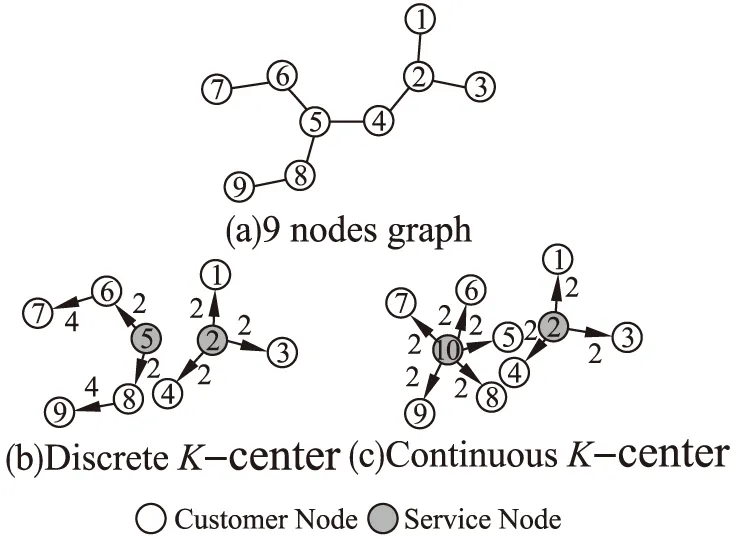
图3 9个客户节点网络服务站部署示意图Fig.3 Schematic diagram of 9 customer nodes network service station deployment
由以上对比可知,连续K中心选址问题更具有普遍性.相对于离散K中心选址问题受到网络拓扑结构制约较大,连续K中心选址问题具有更高的灵活性.为了使得最大加权距离最小、增加网络拓扑的连通性,可以在网络平面适当的添加服务站节点,从而使整个网络的覆盖半径减小.近年来,智能算法已成为解决组合优化问题的重要方法,与其它智能算法相比,PSO算法具有方便实现、不易陷入局部最优等特点,再加上其具有连续搜索的特性,因此PSO算法比较适合求解连续K中心选址问题.
4 加权距离连续K中心问题的SA-PSO算法
粒子群优化算法(PSO)是一种模拟鸟群的觅食过程的进化算法.该算法在连续高维空间搜索极值,快速计算得到最优解,具有方便实现、易编程、设置参数少的优点,适用于大规模的并行计算.由于网络拓扑结构不确定,与进化演化类算法、贪心算法以及其它一些微粒群算法相比,粒子群算法能够根据目标特点,不断调整迭代来适应目标特性,找到全局最优解,从而具有空间局域探索和广域开发均衡的能力.但是传统粒子群算法在求解过程中,收敛速度较慢,搜索结果的鲁棒性也比较差.为了提升算法性能,将模拟退火算法引入到PSO中.模拟退火算法(SA)模拟固体退火降温过程,是一种在大型离散搜索空间中寻找最优的元启发式算法.该算法采用Metropolis重要性采样准则,在搜素过程中接收好的解的同时也接收一定概率的差的解,因此在求解过程中能有效避免陷入局部最优.将模拟退火思想引入粒子群算法,主要是将模拟退火的过程引入到粒子群算法迭代过程中,而PSO算法只产生和更新粒子.这样不仅使得算法的全局搜索能力有所提高,还能保证粒子群的收敛性.基于此,本文提出基于模拟退火的粒子群优化算法(PSO with Simulated Annealing,SA-PSO).
SA-PSO算法中每一个粒子表示的是选址问题中的一组可能解,也就是在R2上编码方式为k个服务站的坐标位置的组合.例如,xi=(xi,1,xi,2,…,xi,2k) 表示第i个粒子的位置,其中xi,2t-1和xi,2t(t=1,…,k)分别代表在平面R2上第t个服务站中的横纵坐标.使用公式(5)来计算粒子i的适应值,适应值越大,选址位置越差;反之,选址的位置越好.
(5)
在SA-PSO算法的迭代过程中,粒子通过与其他粒子相互作用,根据适应度函数不断调整飞行速度(速率和方向)以及对整个群体的状态信息进行更新,得到全局最优解.公式(6)展示了粒子调整飞行速度和更新位置的方法.其中:w为惯性权重,c1和c2分别为自我学习因子和社会学习因子,都是非负数.vi=(si,1,si,2,…,si,2k)为第i个粒子的飞行速度,pi=(pi,1,pi,2,…,pi,2k)为第i个粒子搜索到的最优位置,pg=(pg1,pg2,…,pg2k)为粒子群搜索到的最优位置.在迭代过程中,xnew将以某一概率取代原来的最优位置x,这一概率采用温度T来控制.温度T的变化Tt=α·Tt-1,会随着算法的执行缓慢下降.其中α∈(0.95,0.99),Tt为粒子群第t次迭代的次数,r为退火常数.公式(7)为概率p的计算公式,其中:ΔE=F(xnew)-F(x).
(6)
(7)
上文提到PSO算法是模拟鸟类觅食等群体行为,那么SA-PSO算法则是一群具有更高“智商”的“鸟”,它是以某种概率“试探”后再决定其觅食方向,而不是盲目地直接扑向下一个位置.因此,当温度下降足够慢时,粒子不会轻易跳出有可能的搜索区域,使得粒子的局部搜索能力增强.根据上述思想,可采用SA-PSO算法解决连续型的K中心选址问题,其步骤描述如下:
Step 1.构建节点的网络图,随机产生粒子数目为PopSize的种群,设置c1和c2的值,确定w和T的计算方式.
Step 2.在搜索范围内初始化粒子的位置x和速度vi.
Step 3.根据设定的参数计算每个粒子的适应值F(xi).
Step 4.每次迭代过后,更新粒子和种群的最优位置pbest以及gbest.
Step 5.由公式(6)对位置x和速度vi进行更新.
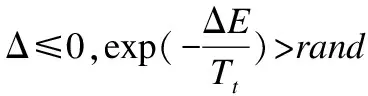
Step 7.当粒子的适应值收敛或者达到了最大迭代次数时,算法结束运行;否则返回Step 3.
SA-PSO算法求解连续K中心选址问题的描述为:

算法1.求解连续K中心选址问题的SA-PSO算法输入:节点网络G,服务站数目k输出:服务站的部署位置1. Initialize Population,T0,α,Maxgen,r,pbest=x,and so on 2. form=0 to Maxgen-1 3. Tm+1=α×Tm; 4. gbest=min(pbest);5. for i=1 to PopSize6. if f(xi)
5 仿真分析
本节的实验环境是:Matlab2012a,内存4GB,CPU主频为3.4GHz的双核计算机.实验分别采用50、100、300和500节点的网络规模仿真连续K中心选址问题,网络为节点度属于集合[1,11]的随机网络.实验以最小覆盖半径作为优化目标,将SA-PSO算法与K-means算法和GA算法进行实验对比.
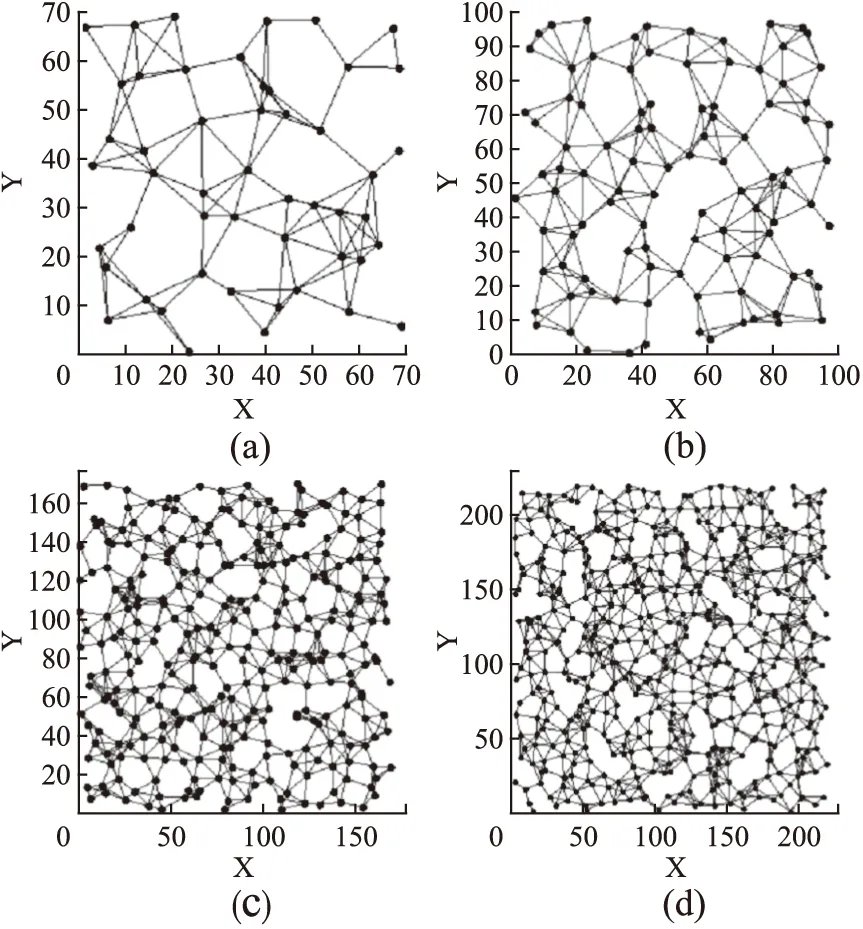
图4 4种规模的网络拓扑图Fig.4 Different scale network topology diagrams
5.1 算法实验结果分析
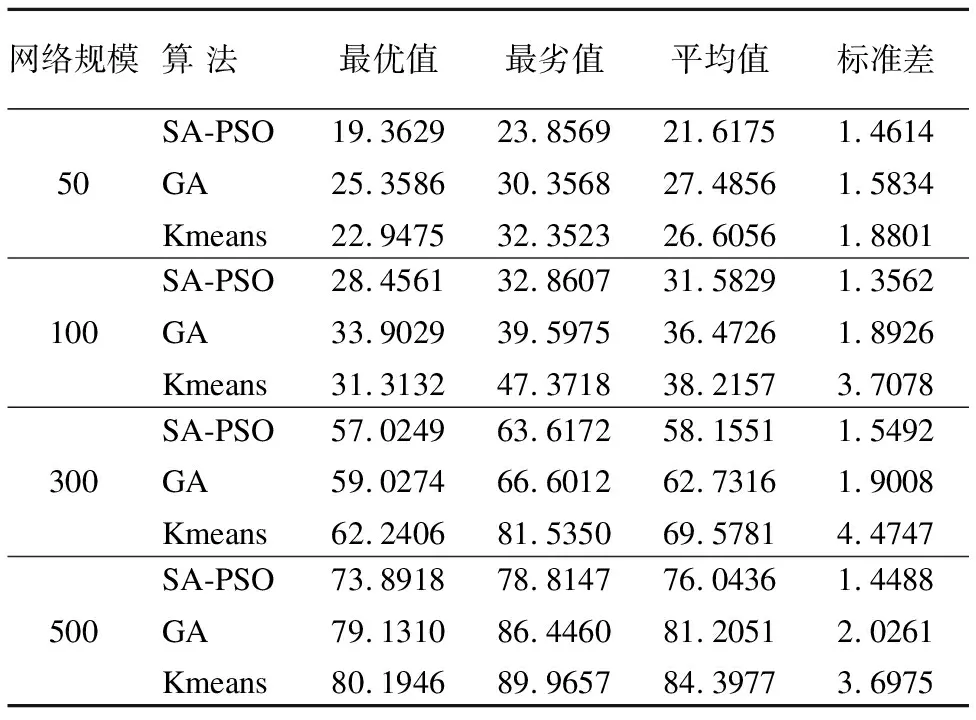
表1为在固定服务站数目为5的情况下SA-PSO算法、GA算法、K-means算法3种算法在50、100、300、500节点网络规模中的优化结果.表1为20次独立试验结果.
观察表1可知,对网络的覆盖半径而言,SA-PSO算法在不同网络规模情况下的整体优化效果要优于其他两种算法.K-means算法一般将服务站的位置设置在R2-V(G)中,但由于其网络拓扑结构的关联较低,容易陷入局部最优,这会导致服务站的选取位置较差,因此K-means算法的优化效果整体上比SA-PSO算法和GA算法要略为逊色.SA-PSO算法有较小的标准差,其稳定性强于其他算法.由于SA-PSO算法在粒子群优化算法中引入了模拟退火机制,这使得算法能够更加快速的收敛于全局最优解,提高全局搜索精度,稳定性也有所增强.
表1 3种算法在4种不同规模网络的优化结果
Table 1 Optimization results of four algorithms on networks
of different sizes
网络规模 算 法最优值最劣值平均值标准差50SA-PSOGAKmeans19.362925.358622.947523.856930.356832.352321.617527.485626.60561.46141.58341.8801100SA-PSOGAKmeans28.456133.902931.313232.860739.597547.371831.582936.472638.21571.35621.89263.7078300SA-PSOGAKmeans57.024959.027462.240663.617266.601281.535058.155162.731669.57811.54921.90084.4747500SA-PSOGAKmeans73.891879.131080.194678.814786.446089.965776.043681.205184.39771.44882.02613.6975
5.2 算法收敛过程及时间复杂度分析
图5表示的是不同网络规模下SA-PSO算法、GA算法和K-means算法的迭代收敛过程,图A-D的分别为50,100,300,500节点的网络规模.
观察图5可知,在4种网络规模中,3种算法收敛过程较为明显;K-means算法得初始值大于SA-PSO算法和GA算法;而SA-PSO算法与另外两种算法的收敛值有较大差异.初始值大其效果较差,因此K-means算法的整体效果要劣于GA算法与SA-PSO算法.K-means算法初始值大的原因主要是由于其初始位置是在稀疏的随机网络平面R2内生成,这使得客户节点与服务站的连接度低.从收敛过程可以看出,GA算法收敛最慢;SA-PSO算法收敛速度较快,K-means算法收敛速度最快,但是容易陷入局部最优.但是SA-PSO算法具有空间局域探索和广域开发均衡能力,可以较快的收敛于全局最优解.
从算法理论分析,K-means算法的时间复杂度为O(n.k.t),遗传算法GA的时间复杂度为O((n-k)2kt.NP),SA-PSO的算法时间复杂度为O(n.k.t.IP).其中,n表示网络节点数,k表示部署的网关数目,t为算法的迭代次数,NP为遗传算法的种群规模,IP为粒子群算法初始化种群数量.
5.3 服务站部署效果分析
如果固定服务站的数目,其部署效果并不会随网络规模的增加而产生特别明显的效果.因此,如图6所示,实验以3种算法在服务站固定为5的50节点和100节点的两种随机网络规模进行效果对比.
由图6观察各算法的网关位置可知,SA-PSO算法与K-means算法在网络平面R2中设置服务站,而GA算法则直接在客户节点中设置网关.SA-PSO算法选取几个非邻接节点的几何中心位置设置服务站,其节点度较大,并且客户节点之间的距离也能够有效的减少.所以相对于K-means算法,SA-PSO算法设置的网关位置更为合理,簇的规模差异大会使得网络拓扑结合零散化,对于减小网络覆盖半径不利.由图6观察3种算法的簇可知,GA算法和K-means算法的簇规模相差较大,而SA-PSO算法中的簇簇规模几乎相等.因此SA-PSO算法不仅使得网络覆盖半径最小还能兼顾各个网关,让其负载均衡,提高服务站的效率.在相同服务站数目情况下,SA-PSO算法求解的网络覆盖半径均比GA算法和K-means算法都要小.因此具有较小的初始值以及稳定性较强的SA-PSO算法更适合用于求解连续K中心选址问题.
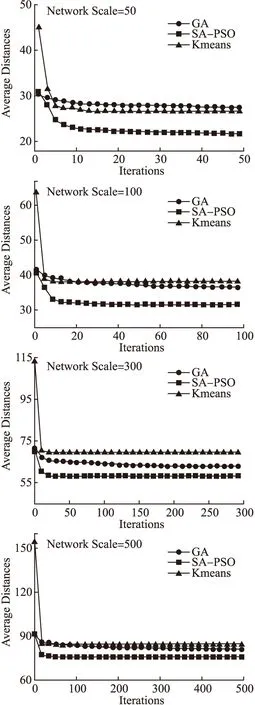
图5 3种算法的收敛过程对比Fig.5 Comparison of the convergence process of the three algorithms
6 结 论
本文研究的是连续K中心选址问题,降低客户节点到服务站节点之间的加权距离.本文以最小加权距离作为优化目标,通过将模拟退火机制引入PSO算法并且加入惯性权重等改进策略,本文提出改进的粒子群优化算法(SA-PSO).通过
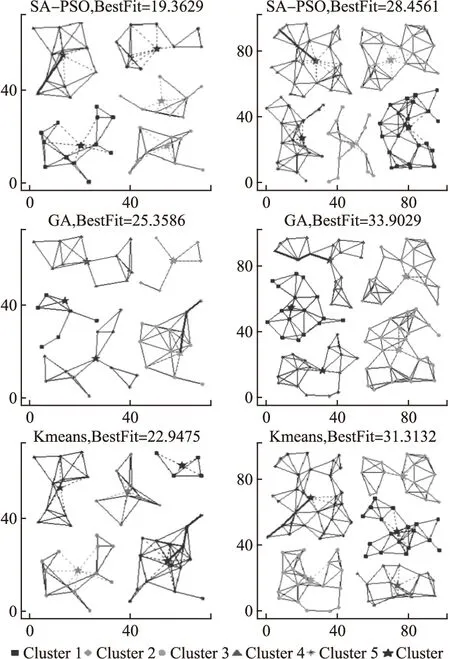
图6 3种算法的服务站部署效果Fig.6 Service station deployment effect of three algorithms
对比其他算法,SA-PSO算法可以较快的收敛于全局最优解.本文的研究对设施连续K中心选址问题具有重要的应用价值,也为选址问题提供了一种新颖的思路和解法.
