带柯西变异的自学习改进烟花算法
2020-05-09赵志刚李智梅
曾 敏,赵志刚,李智梅
(广西大学 计算机与电子信息学院, 南宁 530004)
1 引 言
烟花算法(Firework Algorithm,FWA)[1]是在2010年由Tan等人提出来的一种新型群智能优化算法,通过模拟烟花在空中爆炸的行为来建立相关的数学模型,通过随机因素以及选择策略形成的一种并行爆炸式搜索方式,具有求解速度快、隐并行性的特点,成为了能够求解复杂优化问题最优解的一种全局概率搜索方法.现已被广泛的运用在各种实际优化问题的求解,包括优化调度[2]、微波成像[3]、电网营运管理[4]、图像识别[5]、聚类[6]、路径规划[7]等.截止2019年三月,Google学术搜索显示,烟花算法的首创论文已经被应用了470次.
和其他智能优化算法类似,烟花算法存在有收敛速度慢、求解精度不高等缺陷.对烟花算法的优化主要分为两类:一是对基本烟花算法算子进行分析与改进.文献[8,9]分别提出了对火花生成策略和爆炸半径进行改进的EFWA和AFWA;文献[10]通过引入反向学习策略和动态记忆反馈的机制,提出一种烟花算法优化算法;文献[11]充分利用了爆炸火花的信息,从信息利用的角度提出了 GFWA.文献[12]改进选择策略,提出了ISSFWA;二是与其他启发式算法相结合提出混合算法.文献[13]将差分算法的差分变异替代烟花算法的高斯变异,提出了 FWA-DM.文献[14]将生物地理学优化算法中的迁移算子引入烟花算法提出了的 BBO-FWA 算法,具有较强的勘探能力.文献[15]将进烟花算法和蚁群算法相结合提出一种混合算法并应用在避障路径规划.
为了进一步提高标准烟花算法的性能,本文提出一种新的改进烟花算法.该算法将高斯变异算子更换为全局搜索能力更强的柯西变异算子;用全局最优烟花个体和历史柯西火花的位置信息来构造新的爆炸半径;并提出一种可以同时兼顾烟花质量与分布的挑选策略.使用10个常用的基准测试函数和10个0-1背包问题对该改进算法的性能进行测试,并将其与经典的蝙蝠算法(BA)、粒子群算法(SPSO)、带高斯扰动的粒子群算法(GPSO)、烟花算法(FWA)、增强烟花算法(EFWA)、自适应烟花算法(AFWA)进行对比实验.
2 分种群自学习改进烟花算法
2.1 柯西变异策略
在大规模数据集下,算法解决这类解空间较大的问题要求较高的全局搜索能力.因此,改进算法将标准烟花算法中的高斯变异算子更换为全局搜索能力更强的柯西变异算子,增大变异范围,提高全局搜索能力.柯西分布的图形似一个钟形,两翼宽,加大了寻优范围,如图1所示,标准柯西分布在零点附近的波峰低于标准高斯分布,但两边趋向于零的速度比高斯分布要慢,由此可见柯西变异的扰动能力比高斯变异强,变异范围更广,较容易跳出局部最优.
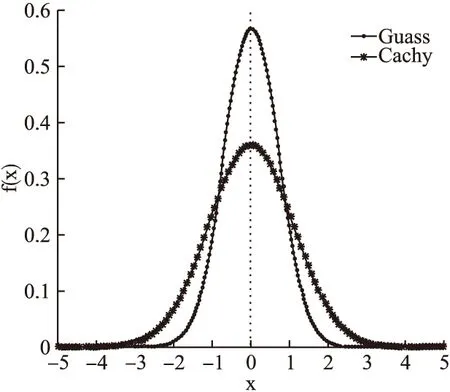
图1 标准高斯分布和标准柯西分布概率密度曲线对比图Fig.1 Comparison of probability density curves of standard gaussian distribution and standard cauchy distribution
柯西变异的计算公式为:
(1)
其中,Cauchy(0,1)是标准柯西分布函数,p为随机变异概率.
2.2 自适应爆炸半径
在烟花算法中,根据烟花种群个体的适应度值来计算爆炸火花数量以及爆炸半径,适应度值较好(较小)的烟花个体往往拥有较小的爆炸半径,即在较优烟花个体周围进行更加详细的局部搜索;适应度值较差(较大)的烟花个体拥有较大的爆炸半径,及达到扩大搜索范围发挥全区搜索的效果,以此来平衡全区搜索和局部搜索的能力.在基本烟花算法中,爆炸幅度按照公式(2)计算.
(2)
当前烟花的适应度值等于Ymin时,此时烟花即为目前为止找到的最好的烟花,此时当前最好烟花所对应的爆炸幅度过小,起不到局部开发的作用,甚至会丧失局部挖掘能力,这样就会浪费当前找到的最好烟花的资源.且从标准烟花算法的选择策略可知,没有被选为下一代的候选集高斯变异火花被丢弃,这样则浪费了大量候选集火花资源.
为了使改进算法的爆炸半径能及时地对搜索方向进行引导和限制,最理想的状态是迭代初期,爆炸半径较大来加强全局探索能力;迭代后期,爆炸半径较小来以增强局部搜索能力,加快算法收敛.使算法求解精度与搜索速度达到一种平衡.
本文以信息利用的角度,以爆炸火花个数作为分种群依据,将烟花种群分为3类:在每一次迭代的烟花种群中,对于一个最小化问题,处于目前最优位置的烟花为核心烟花,拥有大于均值爆炸火花数的烟花为优质烟花,拥有小于均值爆炸火花数的烟花为良好烟花,不同类型烟花能够自适应的调整爆炸半径.为充分利用核心烟花,在核心烟花附近进行高斯扰动来进行更为详细的局部搜索;优质烟花向目前为止找到的最好的烟花位置学习,达到向对当前种群内最优秀的个体gbest学习的效果;良好烟花则向柯西火花历史位置CauchySparkPbest学习,增加种群多样性.烟花个体分种群的自适应爆炸半径如下:
(3)
其中,CPbesti为柯西火花历史位置信息,gbest为当前最好烟花即最优烟花的位置信息,SNi为第i个烟花产生的爆炸火花数量,SNavg为种群爆炸火花数的平均值,N(0,1)是服从均值为0,方差为1的高斯分布函数.
2.3 精英-随机选择策略
标准烟花算法中,选择策略是基于欧式距离的,这种计算方式导致时间消耗很大,因此改进算法采取“精英-随机”选择策略,即从烟花、爆炸火花、柯西火花组成的候选集,选取适应度值最好的一个个体作为下一代烟花的“精英”,其余popsize-1个则从候选集中随机选取(可以重复选择).这样既保证了保留最优个体对烟花种群的领导,又保证了种群的多样性且降低了计算复杂度.
2.4 算法流程
根据2.1~2.3小节,在标准烟花算法的基础上,本文提出了一种新的烟花算法改进算法——带柯西变异的自学习改进烟花算法(Self-Learning Improved Fireworks Algorithm with Cauchy Mutation,SiFWA),该算法的算法流程如下:
算法1.分种群的自学习改进烟花算法步骤
输入:烟花种群初始位置
输出:烟花种群的位置和全局最优解
Begin
1.初始化烟花种群;
2.确定生成子代火花数量;
3.根据公式3和2.2小节按不同种群分别计算爆炸半径;
4.根据2.2小节生成子代爆炸火花;
5.母代烟花根据公式1生成柯西火花;
6.按照公式6对超出边界的火花进行越界处理;
7.在烟花母代、爆炸烟花子代、柯西火花组成的候选集中,根据“精英-随机”选择策略选出下一代烟花;
8.重复Step 2-Step 7,直到达到终止条件,停止迭代.
End
在步骤2中,第i个烟花产生爆炸火花个数Si定义为:
(4)
为了限制烟花爆炸产生火花的数量,进行以下条件限制:
(5)
在寻优的过程中,需要对越界的烟花进行如下越界处理:
(6)
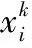
3 实验设置与结果分析
3.1 实验设计
10个基准测试函数如表1所示,其中f1~f6维度为30dim,
表1 基准测试函数
Table 1 Benchmark functions

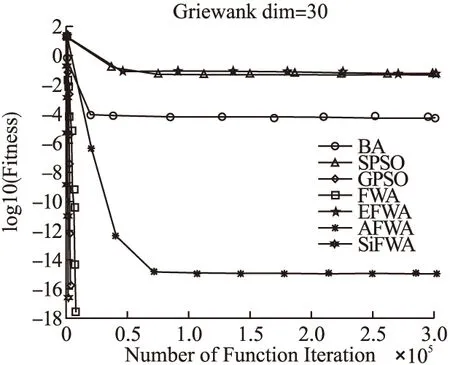
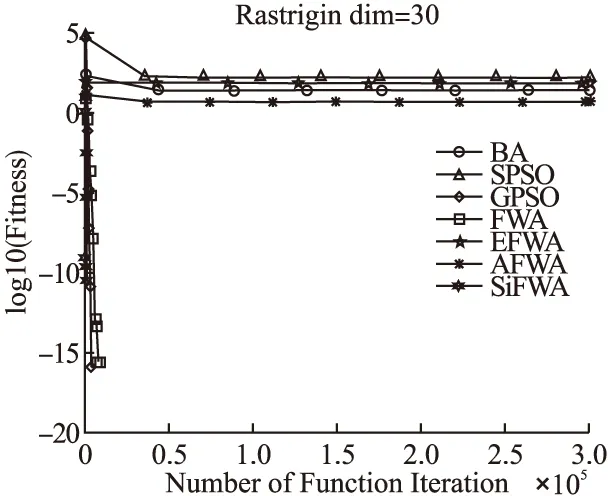
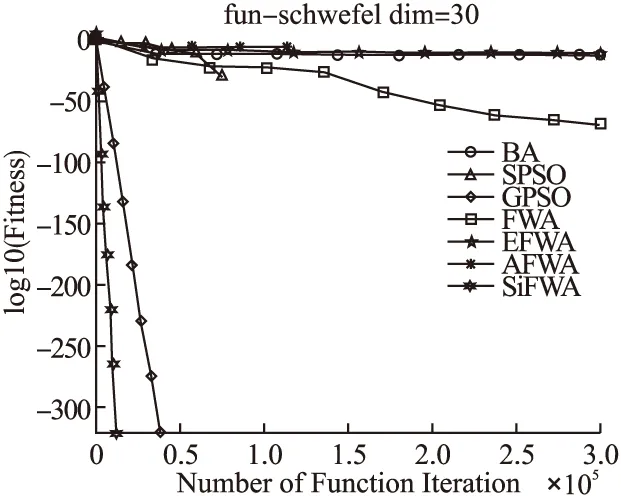
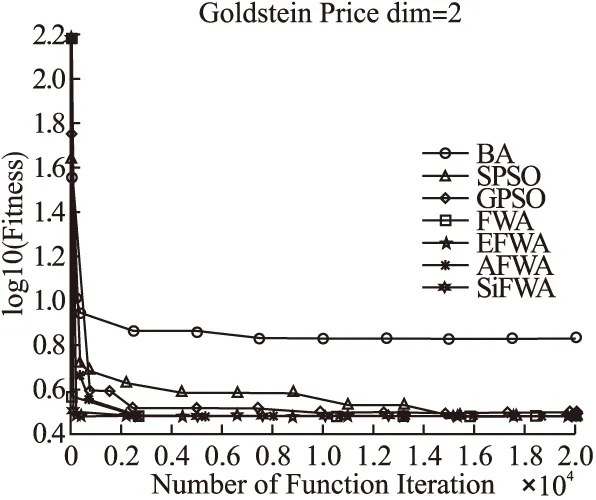
FunNameFuntionDimDomain最优点最优值Spheref1=∑ni=1x2i30[-100,100]d(0,0,…,0)0Rosenbrockf2=∑ni=1[100(xi+1-xi)2+(xi-1)2]30[-30,30]d(0,0,…,0)0Griewankf3=14000∑ni=1x2i-∏ni=1cos(xii)+130[-600,600]d(0,0,…,0)0Rastriginf4=∑ni=1(x2i-10cos(2πxi)+10)30[-5.12,5.12]d(0,0,…,0)0Ackleyf5=-20exp(-0.2∑ni=1x2i)-exp(1n)∑ni=1cos(2πxi)+20+e30[-32,32]d(0,0,…,0)0Schwefelf6=∑ni-1(∑ij=1xj)230[-100,100]d(0,0,…,0)0Six-Hump Camel-Backf7=4x21-2.1x41+13x61+x1x2-4x22+4x422[-5,5]2∗-1.0316285Goldstein Pricef8=[1+(x1+x2+1)2(19-14x1+3x21-14x2+6x1x2+3x22)]·a[30+(2x1-3x2)2(18-32x1+12x21+48x2-36x1x2+27x22)]2[-2,2]2(0,-1)3Schaffer’s F6f9=sin2x21+x22-0.5[1+0.001(x21+x22)]2+0.52[-100,100]2(0,0)0Braninf10=(x2-5.14π2x21+5πx1-6)2+10(1-18π)cosx1+102-5 f7~f10维度为2dim.“*”表示该函数不止一个最优点.并与蝙蝠算法(BA)[16]、标准粒子群算法(SPSO)[17]、带高斯扰动的粒子群算法(GPSO)[18]、标准烟花算法(FWA)[1]、增强烟花算法(EFWA)[8]、自适应烟花算法(AFWA)[9]进行对比实验. 改进算法的烟花种群大小设置为5,火花总数设置为50,柯西火花数量设置为5.BA算法的参数设置参考文献[16],SPSO算法的参数设置参考文献[17],GPSO算法的参数设置参考文献[18],FWA算法的参数设置参考文献[1],EFWA算法的参数设置参考文献[8],AFWA算法的参数设置参考文献[9].为估计改进算法的性能,且保证模拟仿真实验的公平性,我们将对表1的基准测试函数设定独立运行次数为run_num=51,最大评价次数MaxIteration=104×dim次.种群初始解的质量在一定程度上影响最终解的质量,为了避免初始位置对实验的影响,在同一测试函数上,7种算法均使用同一组初始位置.测试得到最坏值worst、最好值best、平均值avg、标准方差std见表2,寻优成功率SR见表3、将10个测试函数寻优的平均值作为衡量算法收敛性的指标,以标准方差值作为衡量鲁棒性的指标. 表2 7种算法实验结果对比 algfunworstbestavgstdfunworstbestavgstdBA1.06E-036.95E-049.10E-049.92E-054.44E-118.47E-185.43E-129.30E-12SPSO7.47E-015.37E-022.67E-011.53E-010000GPSO00000000FWAf10000f61.08E-1371.71E-2032.31E-1391.51E-138EFWA1.23E-015.10E-029.07E-021.62E-024.10E-085.38E-125.81E-099.13E-09AFWA4.12E-183.00E-224.34E-199.01E-190000SiFWA00000000BA2.95E+011.67E+012.44E+012.87E+00-1.0316280-1.0316285-1.03162849.83E-08SPSO6.66E+033.75E+016.86E+021.35E+03-1.0316285-1.0316285-1.03162852.61E-16GPSO2.87E+012.82E+012.86E+011.16E-01-1.0316285-1.0316285-1.03162852.61E-16FWAf22.85E+012.47E+012.56E+015.39E-01f7-1.0316284-1.0316285-1.03162842.55E-09EFWA5.05E+033.33E+014.96E+021.06E+03-1.0316285-1.0316285-1.03162851.72E-11AFWA9.60E+022.07E+011.59E+022.48E+02-1.0316285-1.0316285-1.03162853.52E-16SiFWA2.46E+012.38E+012.42E+011.61E-01-1.0316284-1.0316285-1.03162851.75E-09BA5.61E-053.23E-054.59E-055.90E-0630.00002193.00000016.70588659.38E+00SPSO9.79E-029.21E-034.28E-022.01E-023.00000003.00000003.00000001.58E-15GPSO00003.00000003.00000003.00000001.58E-15 续表 为了对收敛速度和收敛精度的观察更加的直观,文中给出图2至图7的寻优进化曲线.为缩减篇幅,仅给出部分基准测试函数的寻优进化曲线.其中纵坐标中的适应度值均取对数log10,即log10(Fitness). 图2 f1寻优进化曲线Fig.2 Evolution curve of f1 图3 f3寻优进化曲线Fig.3 Evolution curve of f3 在f1、f3、f4、f6、f9的寻优过程中,分析图2,图3,图4,图5,图7:在寻优前期,在相同的评价次数下,SiFWA的收敛速度和收敛精度都优于其他6种对比算法.分析表2中所对应的平均解avg:SiFWA均找到了最优解,且不亚于其他6种对比算法. 图4 f4寻优进化曲线Fig.4 Evolution curve of f4 图5 f6寻优进化曲线Fig.5 Evolution curve of f6 在f2、f5的寻优过程中,分析表2中所对应的平均解avg:迭代结束时对于f2,SiFWA所寻平均解avg优于其他6种对比算法;对于f5,SiFWA所寻平均解avg不亚于其他6种对比算法. 在f7、f8、f10的寻优过程中,分析表2中所对应的平均解avg:寻优结束后SiFWA所寻平均解avg不亚于其他6种对比算法. 综上所述,SiFWA算法的总体收敛性能优于其他6种对比算法. 图6 f8寻优进化曲线Fig.6 Evolution curve of f8 图7 f9寻优进化曲线Fig.7 Evolution curve of f9 寻优精度设置为λ=10-5,也就是说如果所寻解的绝对值与理论最优解的绝对值的差值小于或等于该精度值时,记录寻优成功一次.表3所对应的寻优成功率可知:对于f2、f107种算法均没有找到理论最优值;对于f1、f3、f4、f5、f6、f7、f8、f9,SiFWA的寻优成功率均为100%,优于其他6种对比算法. 综上所述,MAFWA算法的总体寻优成功率优于其他6种对比算法. 表3 7种算法寻优成功率(%) algf1f3f4f5f6f7f8f9f2,f10BA000010010082.3566.670SPSO000010010010066.670GPSO10010010010010010010066.670FWA1001001001001001001001000EFWA000010010010098.040AFWA10049.0221.5772.510010010049.020SiFWA1001001001001001001001000 算法鲁棒性可反映在标准方差std上,std值越小,算法鲁棒性越好;std值越大,算法鲁棒性则越差.分析表2中对应的标准方差std一栏:在f1、f3、f4、f5、f6、f9的寻优过程中,SiFWA算法所得的标准方差std均为0,表现出较好的稳定性.在基准测试函数f2的寻优过程中,SiFWA算法所得的标准方差std比BA、SPSO、FWA、EFWA、AFWA小,大于GPSO;在f7的寻优过程中,SiFWA算法所得的标准方差std比BA、FWA小,大于SPSO、AFWA、GPSO、EFWA;在基准测试函数8的寻优过程中,SiFWA算法所得的标准方差std比BA、FWA小,略大于SPSO、GPSO、EFWA、AFWA;在基准测试函数f10的寻优过程中,SiFWA算法所得的标准方差std比BA、SPSO、GPSO、EFWA小,略大于FWA、AFWA. 综上所述,SiFWA的总体鲁棒性能优于其他6种对比算法. 综上所述,本文出的改进SiFWA算法,使用全局搜索能力更强的柯西变异算子来替代高斯变异算子,增大变异范围,提高全局搜索能力,增加了种群多样性;从“信息利用”的角度,用全局最优烟花个体和历史柯西火花的位置信息来构造新的爆炸半径,解决了爆炸幅度设定困难的问题,自适应式的爆炸半径使得烟花种群能在在迭代过程中学习有价值的历史信息,使其不仅能够继承和学习历史信息,而且能够自适应地调整步长;并使用“精英-随机”选择策略,同时兼顾烟花质量与分布.由仿真实验结果可知,改进算法有效的平衡了全局搜索和局部开发能力,在求解精度和稳定性表现出较好的性能. 通过仿真实验,SiFWA在解决连续优化问题上有较好表现,离散优化是最优领域一个非常重要的分支,是应用数学和计算机科学中优化问题的重要分支.为了进一步验证本文提出的算法的有效性,我们将其应用于离散优化问题中的求解 0-1 背包问题(Knapsack Problem,KP).0-1背包问题的数学模型如下: (7) (8) 其中,n为物品的数量,pi和vi表示第i个物品拥有的价值和体积,Vmax表示背包的最大体积限制,自变量xi表示物品的状态,0表示没有被装进背包,1表示被装进背包.其中每个物品最多被装入背包一次,且只能完全装入,不允许部分装入. 现需考虑在不超过背包容积的前提下,怎样使装入背包中的物品总价值最大.使用罚函数法最大化问题转化为最小化问题,0-1背包问题转化为: (9) 0-1背包问题属于离散类型问题,在算法应用时应将烟花种群个体的位置信息进行离散化处理,其具体操作如下: (10) 其中,x(i,j)表示第i个个体第j维离散化处理前的位置信息,x′(i,j)表示第i个个体第j维离散化处理后的位置信息. SiFWA算法求解0-1背包问题的伪代码参照2.4小节,但是在计算个体的适应度值之前,需要根据公式(10)对其位置进行离散化处理. 对于其他6种对比算法(BA,SPSO,GPSO,FWA,EFWA,AFWA)进行同样的离散化处理之后,对实验结果进行比较.算法比较过程选用文献[19]中的10个常见的0-1背包问题. 求解0-1背包问题的相关参数设置:最大迭代次数为104×dim次;设置独立重复运行次数为30次;其他参数设置参照3.1小节,对比实验的结果如表4所示. 表4 0-1背包问题结果分析 algexampleworstbestavgstdSR(%)exampleworstbestavgstdSR(%)BA29529529501005252520100SPSOf11252295289.531.14E+01434752511.58E+0060GPSO252295289.631.29E+0150f16495251.578.60E-0177FWA288295294.571.38E+0087455251.571.33E+0080EFWA29529529501005252520100AFWA29529529501005252520100SiFWA29529529501005252520100BA10241024102401001071071070100SPSO9191024981.272.57E+0113f1793107105.32.81E+0050GPSOf129291024980.732.71E+017102107104.931.39E+0017FWA9021024973.933.39E+01796107106.632.01E+0097EFWA10241024102401001071071070100AFWA10241024102401001071071070100SiFWA10241024102401001071071070100BA3535350100976197679764.071.93E+0010SPSO3535350100974197679754.87.01E+003GPSOf13333534.933.70E-0197f189727976797558.55E+003FWA3535350100973497659755.57.44E+000EFWA35353501009767976797670100AFWA35353501009767976797670100SiFWA35353501009767976797670100BA23232301001301301300100SPSO2323230100118130128.83.66E+0090GPSOf142323230100118130129.62.19E+0097FWA2323230100f19109130125.88.54E+0080EFWA23232301001301301300100AFWA23232301001301301300100SiFWA23232301001301301300100BA481.0694481.0694481.06942.89E-131001025102510250100SPSO398.3123481.0694456.85128.26408931025978.833.53E+0117GPSO408.0508481.0694459.333323.143390710259823.30E+013FWAf15386.816481.0694464.738531.7467f208661011949.33.69E+010EFWA481.069368481.069368481.0693683.44523E-131001025102510250100AFWA481.069368481.069368481.0693683.44523E-131001025102510250100SiFWA481.069368481.069368481.0693682.89E-131001025102510250100 表4的实验结果显示:由均值avg这一栏可知,SiFWA算法找到的均值不亚于其他6种对比算法,由std这一栏可知:SiFWA算法的鲁棒性不亚于其他6种对比算法.由SR这一栏可知:SiFWA算法的总体寻优成功率不亚于其他6种对比算法.综上,SiFWA算法在求解文献[19]中给出的10个常见的0-1背包问题时,总体性能不亚于其他6种对比算法. 在烟花算法中,爆炸幅度的设定与选择策略是影响算法整体性能的关键.本文提出了一种改进的烟花算法——带柯西变异的自学习改进烟花算法.该算法以搜索能力更强的柯西变异代替高斯变异火花,通过学习利用烟花的历史爆炸信息,自适应地估计后代烟花的爆炸幅度,解决了爆炸幅度这个参数难以设定的问题.使得改进算法在寻优过程中可以很好的平衡全局搜索和局部开发的能力.为了检测算法的有效性,将其应用在了基准测试函数的优化以及求解典型0-1背包问题中,通过对比实验,我们可以知道:与其他6种对比算法相比,带柯西变异的自学习改进烟花算法可以以相对少的评价次数找寻到更好的解,拥有更快的收敛速度和更高的收敛精度.在未来的工作中,将对带柯西变异的自学习改进烟花算法进行更加深入的理论研究,将其应用到更多的工程实践之中.
Table 2 Comparison of experimental results of the 7 algorithms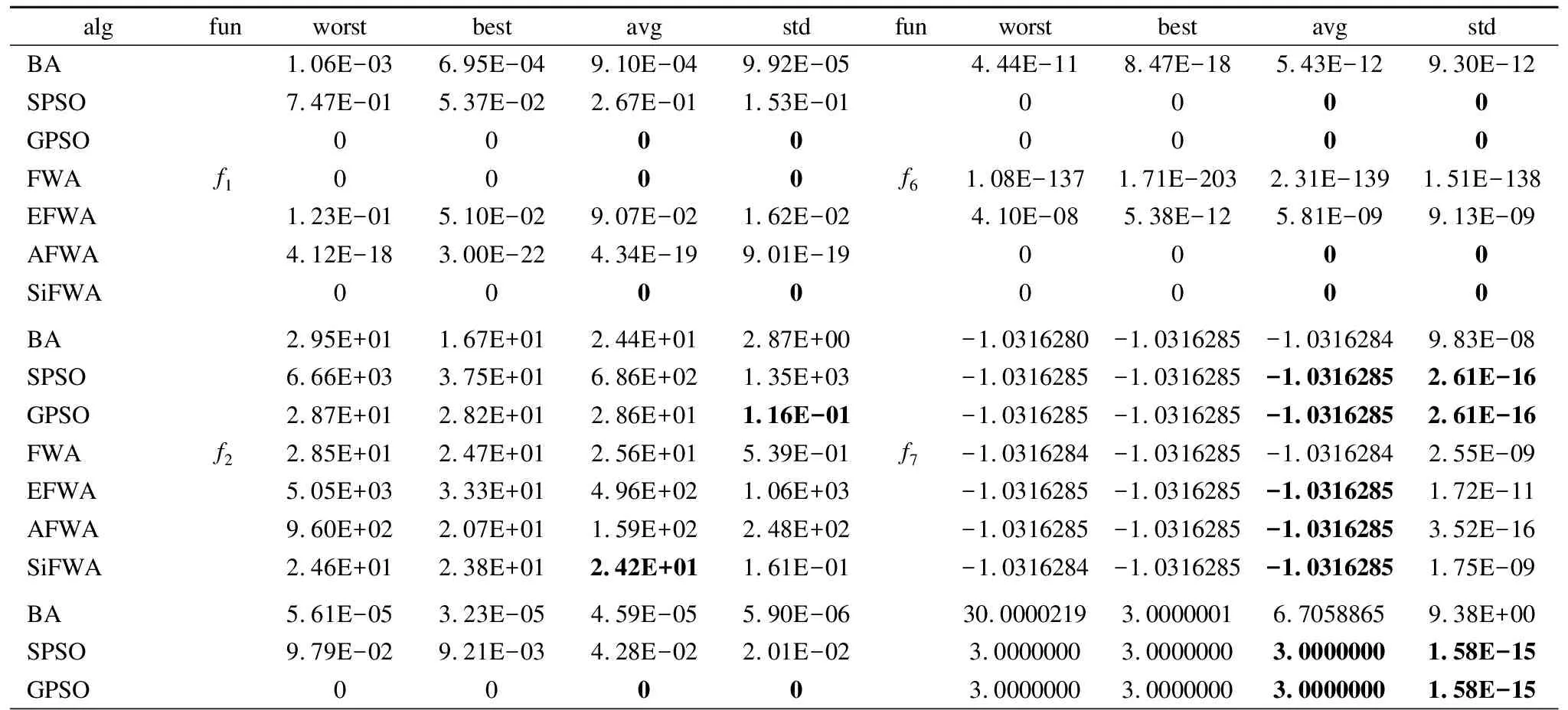
3.2 收敛性分析
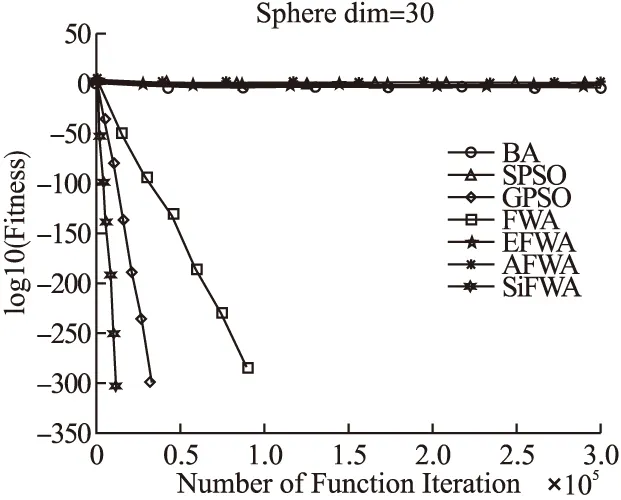
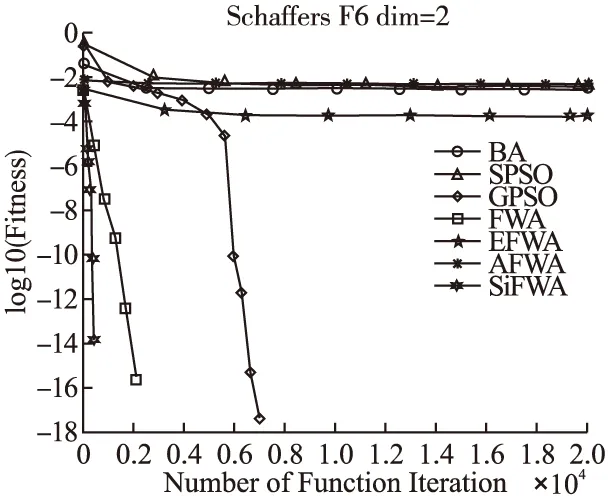
3.3 寻优成功率分析
Table 3 Success rate of seven algorithms(%)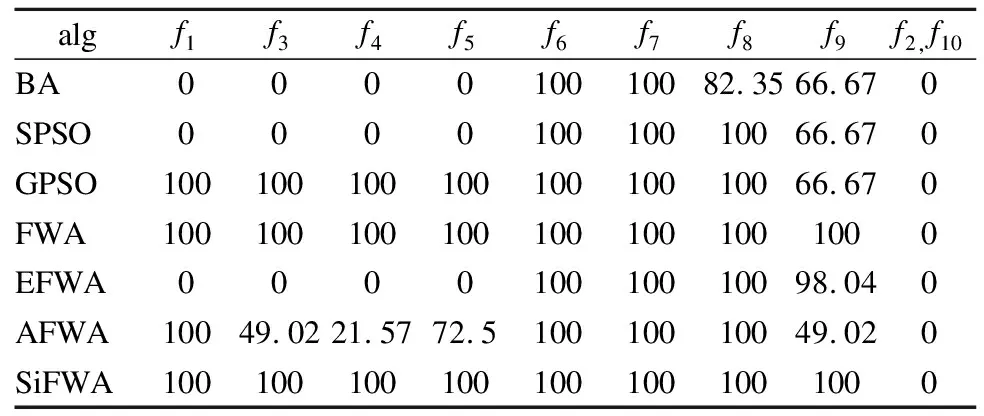
3.4 鲁棒性分析
3.5 讨论
4 算法应用
4.1 0-1背包问题
4.2 算法离散化应用
4.3 对比实验
Table 4 Results analysis of 0-1 knapsack problem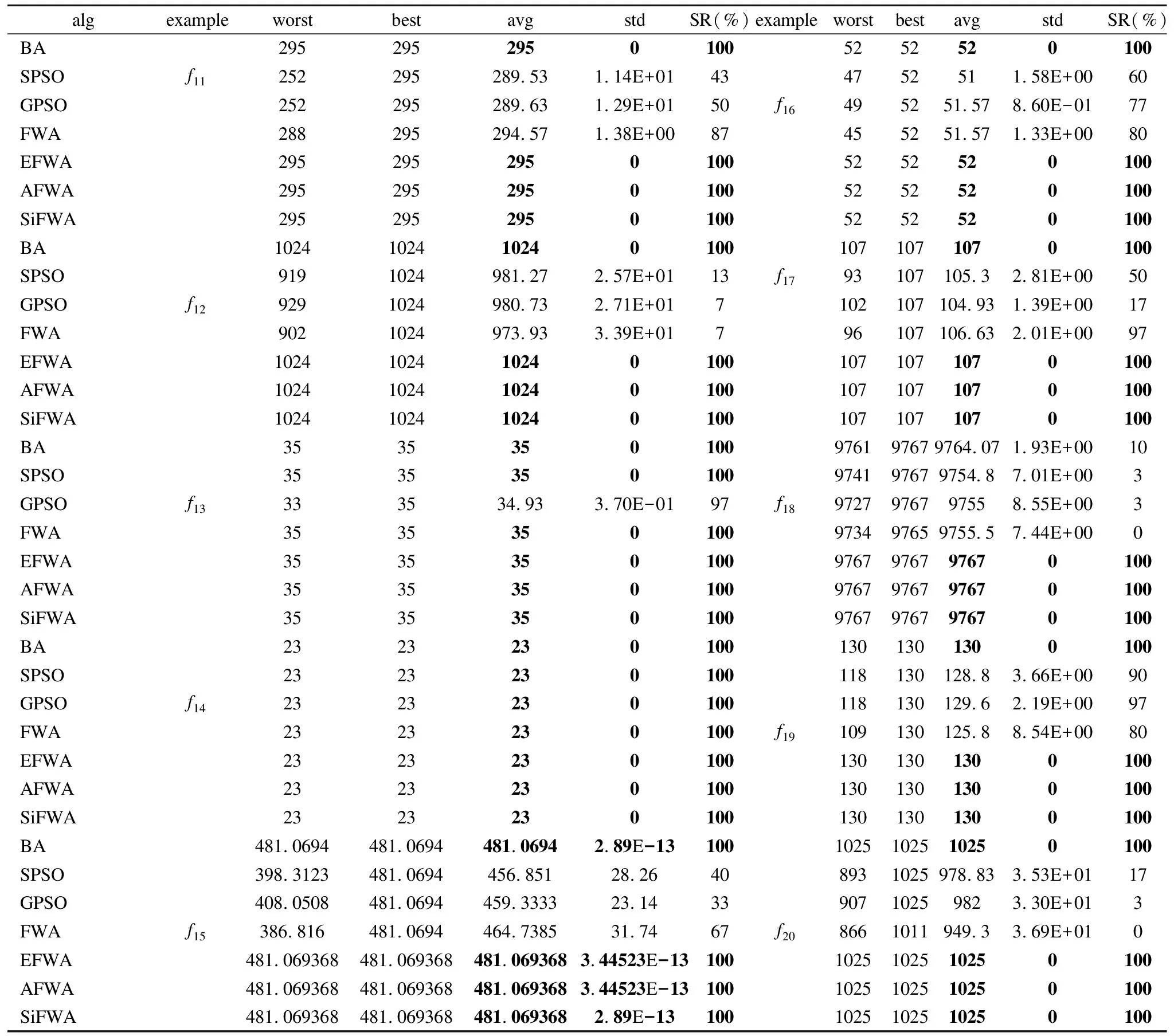
5 结 论
