异构计算环境下基于优先队列划分的调度算法

王 兰，张龙信，满君丰，周立前，李肯立

1(湖南工业大学 计算机学院，湖南 株洲 412007)2(湖南大学 信息科学与工程学院，长沙 410082)

1 引 言

随着云计算和物联网等技术的快速发展，以及新型社交网络的不断涌现，数据正在以前所未有的速度不断地产生和累积，大数据和万物互联的时代已经到来.相对于物联网而言，万物互联在物联网的基础上更侧重于“人”与“物”的互联[1]，增强网络智能，推动人工智能的发展.万物互联的不断发展，网络边缘设备数量亦迅猛地增长.

网络边缘设备和社交媒体等产生海量的、复杂多样的数据，利用云计算中心超强的计算能力来计算和处理数据.数据中心接受到提交的数据任务，采用合理高效的任务调度算法可以提高计算性能、降低数据处理时间.因此，任务调度问题已经成为云计算和边缘计算中的研究热点问题[2]，异构计算模式下的任务调度问题依旧是研究重点问题.

异构计算环境下的任务调度问题已经被证明是NP-hard问题[3]，所以任务调度问题只能通过设计的优化算法取得近似最优解.在并行计算环境下，合理高效的任务调度算法会使处理器系统的计算性能得到很大的提升.任务调度问题是指在满足某些约束条件的情况下(节点间的数据依赖关系和处理器的计算消耗)，按照设计的算法科学地将每个节点任务映射到对应处理器上并高效地执行，以达到最小化任务执行的完成时间、最大化算法的调度效率的目的.任务的有效调度是提高处理器计算性能和资源利用率的关键所在.

任务调度问题一直以来都是高性能计算中的经典问题.根据应用程序的特征(包括任务间的依赖关系、任务在处理器上的计算开销以及任务之间的通信开销)是否提前给定，可将任务调度问题分为静态任务调度和动态任务调度[4].现有的主要研究工作是针对静态任务调度模型，静态任务调度中应用程序的特征是确定的.针对异构系统中的静态调度问题，主要可划分为基于启发式的调度算法和基于引导随机搜索的调度算法，高调度效率的HEFT[4]、CPOP[4]、HCPFD[5]等启发式算法被广泛运用到实际的应用程序中.

随着海量数据的产生和计算数量的增长，异构计算环境下DAG任务图的结构也变得复杂多样化.传统的调度算法在解决复杂问题时可能得不到理想的结果，这需要通过更为合理高效的调度策略来优化和平衡系统的各方面性能[6].目前，国内外研究学者已经提出了很多算法.文献[7]提出了一种前驱节点优先级最早完成时间算法，首先生成前驱节点优先级队列(PPQ)，任务根据向下排名和优先级在PPQ中排队等待调度.文献[8]考虑到任务执行时关键路径上的信息会随着任务调度动态更新，对首任务采用复制技术，然而任务每一次实时更新会增加整个任务的调度复杂性.文献[9]提出了一种基于队列的资源调度模型，其将任务和处理器问题转化成最大费用最小流图，从而有效地优化大规模资源调度.文献[10]针对异构计算系统中的应用程序在使用DVS(动态电压频率调节)技术实现节能时，瞬态故障难以避免.对于具有优先约束的并行任务集，设计了能量约束下的应用程序可靠性最大化算法RMEC.RMEC算法能有效地实现系统高可靠性与能量节约之间平衡的目标.文献[11]提出了数据中心的能量消耗最小和系统失效率最小的双目标优化算法，该算法在不增加时间开销的约束下，能找到更好的pareto front(帕内托前沿).文献[12]提出了最小松弛时间和最小距离(MSMD)算法，该算法针对应用程序截止日期所需的最小VM实例数，在分配的VM实例上调度任务，以达到最小化应用程序的调度时间.以上研究很少针对复杂多样的DAG并行任务集展开研究，因此，本文以提高任务间的并行性和处理器的执行效率为目标，针对多入口、多出口的并行任务集，提出基于优先队列划分调度算法(PQDSA).本文设计的算法将根据入口节点数量确定优先队列数量，划分调度优先队列，将复杂多样的任务集简单化.

本文第一部分介绍了异构计算环境下任务调度的相关背景和现有的研究工作.第二部分阐述了任务调度模型和具体应用模型.第三部分详细介绍了本文提出的算法.第四部分通过实验验证了本方法的可行性和有效性.最后对本文工作进行了总结，并对下一步的研究工作进行了展望.

2 相关知识

2.1 任务调度模型

异构环境下的任务调度问题，是指将具有约束条件的任务按照特定的算法映射到有限的处理器上进行执行.这些任务一般会用DAG图来刻画，任务可以表示为节点，节点是任务调度中的最小单位.当异构计算系统中有任务等待执行时，主机会按照特定算法寻找符合条件的处理器来进行调度，即将任务分配给合适的处理器进行有效调度以达到预期的优化目标.将n个任务调度到m个处理器上的任务调度模型如图1所示.

图1 n个任务调度到m个处理器上调度模型Fig.1 Scheduling model of n tasks scheduled to m processors

2.2 应用模型描述

任务调度是异构计算环境下的关键问题，这种存在约束关系的任务节点可以用DAG图来进行刻画，即G={T，E，W，C}，其中T={ti|(i=1，2，…，n)}表示异构系统中的任务节点集合，n为任务节点总数量.E={eij|eij表示节点ti与节点tj的边}，即节点ti与节点tj之间存在优先约束关系且tj是ti的直接后继节点.C={cij|cij表示ti与tj之间的通信开销，ti是tj直接前驱节点}，cij表示两个任务节点不在同一个处理器上执行时所需的通信开销.W={wij|表示节点ti在处理器pj上的计算开销}，其中pj表示异构系统中第j个处理器，P是处理器的集合，P={p1，p2，…，pm}，m为处理器总数量.如果DAG任务图中不止一个入口或出口节点，我们可以构建虚拟节点作为唯一的入口节点或出口节点，该虚拟节点无通信开销和计算开销.节点调度时必须接收到所有前驱节点的数据才可以进入准备就绪状态，等待调度.如图2所示的DAG任务图，T1-T10表示10个任务节点，有向边上的数字表示节点间的依赖关系，即通信开销.表1描述了任务节点在不同处理器上执行所需要的计算开销.

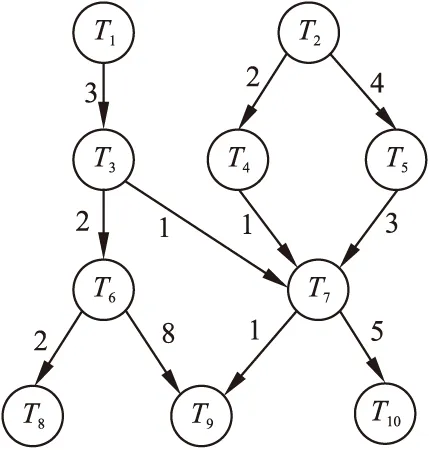
图2 包含10个任务节点的DAG应用模型Fig.2 DAG application model with 10 task nodes

图2所示的DAG图中，各任务节点在处理器上的计算开销如表1所示.为了描述方便，现对任务的开始时间、完成时间、调度长度和调度效率给出以下定义.

表1 任务节点的计算开销
Table 1 Computation cost of task nodes

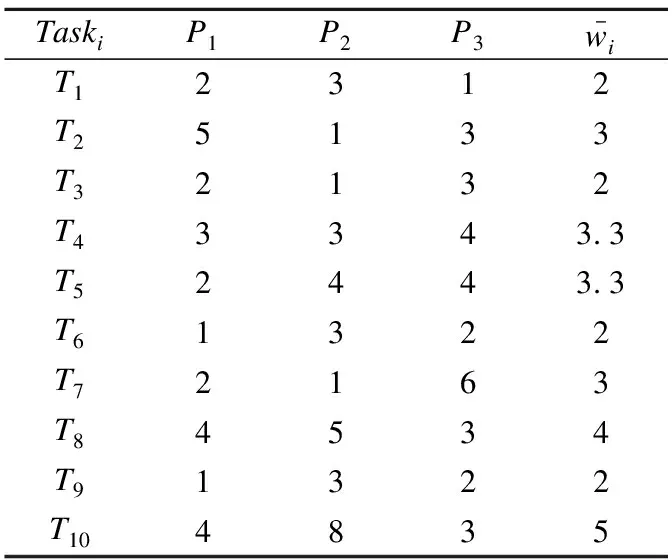
TaskiP1P2P3wi-T12312T25133T32132T43343.3T52443.3T61322T72163T84534T91322T104835

定义1.任务的开始时间、完成时间：若ST(ti，pj)、FT(ti，pj)分别表示任务ti在处理器pj上的开始时间和完成时间，则它们之间的数学关系如式(1)所示：

FT(ti,pj)=ST(ti,pj)+cij

(1)

定义2.前驱节点、后继节点：若pred(ti)表示任务ti的前驱节点，如果任务ti没有前驱节点，则该任务是入口节点.succ(ti)表示任务ti的后继节点，若任务ti没有后继节点，则该任务为出口节点.

任务节点ti平均计算开销定义为：

(2)

其中，wij为任务ti在处理器pi上的计算开销，m为处理器的数量.

节点任务的优先级主要由通信开销、自身在处理器上的计算开销和前驱节点的优先级等三个因素共同决定.

定义3.任务的TL(ti)值：从入口节点开始采用递归的方法计算每个节点的t-level值TL(ti)，其计算表达式为：

(3)

入口节点的TL(ti)的计算表达式如式(4)所示：

(4)

定义4.调度长度(makespan)：若Texit代表出口节点,FT(Texit,pj)表示整个调度的完成时间,若出口节点不止一个,可以添加零计算开销、零通信开销的伪节点作为最后的唯一出口节点,调度长度为：

makespan=max{FT(Texit,pj)}

(5)

调度的最终目的是将节点任务科学地分配到处理器上执行，以达到最小化调度长度的目标.

定义5.调度效率：算法的调度效率(Efficiency)是指任务调度加速比与处理器总数量的比值，其取值范围为0到100%.调度效率由DAG任务的完成时间和处理器的数量共同决定，其计算表达式为：

(6)

其中,m为处理器总数,Speedup为加速比.加速比是指任务集的顺序计算时间与调度长度的比值.

为了描述方便，我们将本文中可能使用到的符号和参数进行归纳，如表2所示.

表2 符号和参数定义
Table 2 Symbol and parameter definition

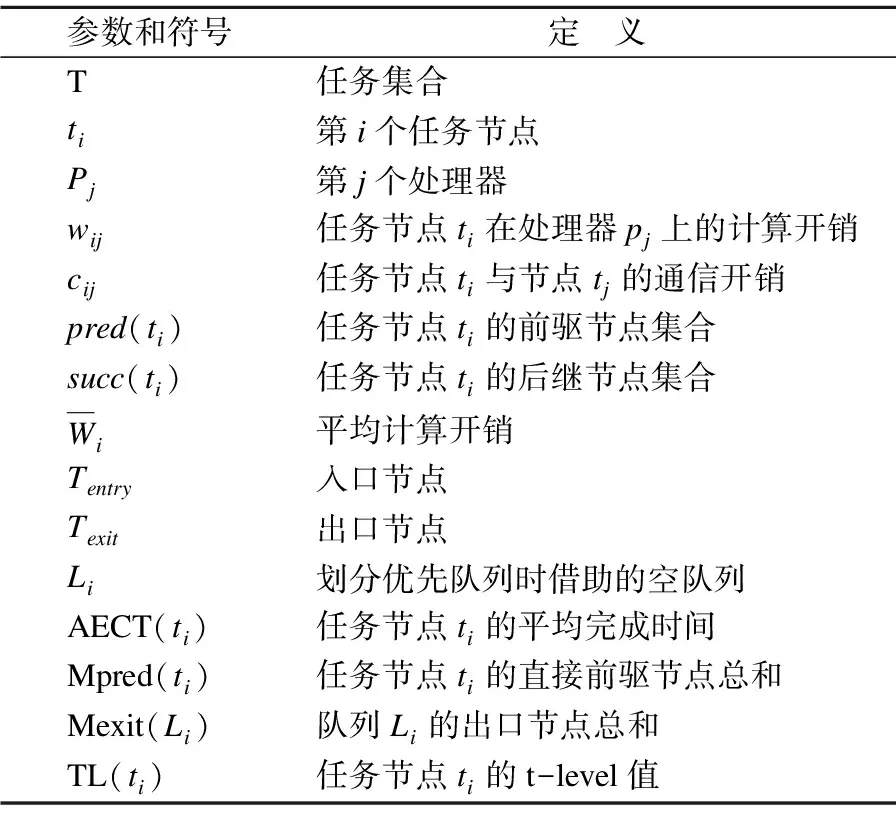
参数和符号定 义T任务集合ti第i个任务节点Pj第j个处理器wij任务节点ti在处理器pj上的计算开销cij任务节点ti与节点tj的通信开销pred(ti) 任务节点ti的前驱节点集合succ(ti)任务节点ti的后继节点集合Wi平均计算开销Tentry入口节点Texit出口节点Li划分优先队列时借助的空队列AECT(ti)任务节点ti的平均完成时间Mpred(ti)任务节点ti的直接前驱节点总和Mexit(Li)队列Li的出口节点总和TL(ti)任务节点ti的t-level值

2.3 问题描述

人工智能的崛起和网络边缘设备的增加以及数据的大量产生，都离不开高性能计算中心的支持.数据的海量产生和高性能计算的高效要求，以及DAG任务图的多变性，都对DAG应用程序的调度提出更高的性能要求.降低DAG任务图节点任务的完工时间以及最大化算法的调度效率，本文侧重于这两个目标.为了达到所要求的目标，第一步在满足约束条件下，对队列进行划分，提高任务间的并行性，以达到降低调度长度的目的.第二步在保证尽可能降低调度长度的前提下，将任务科学地调度到处理器上，以达到最大化处理器的资源利用率[13].

3 优先队列划分调度算法(PQDSA)

众所周知，异构计算环境下的任务调度问题是NP-hard问题[3].为了提高处理器的执行效率和任务间的并行性，本文提出基于优先队列划分的任务调度算法(PQDSA).PQDSA算法的主要思想是根据入口节点的数量，通过计算开销和通信开销来划分合适的优先队列.该算法执行步骤分为优先队列划分、节点优先级以及处理器选择三个阶段.首先，存在数据依赖关系的节点在不同的处理器上执行时，会存在通信开销.为了降低任务集的完工时间，将通信开销较大的任务分配到同一台处理器上执行，以提高调度效率.然后，根据入口节点数量划分的优先队列，计算队列中节点的TL(ti)值，确定节点优先级.最后，在处理器选择阶段，使用基于插入策略的思想，计算出任务完成时间最小的处理器，将其作为该节点的调度处理器，从而进一步缩短调度时间.

3.1 优先队列划分阶段

在优先队列划分阶段，针对复杂多样的DAG任务图，在任务执行调度之前，首先根据入口节点的数量来决定划分多少优先队列.在本文中，从DAG图中的入口节点到出口节点，通信开销和计算开销之和最大的路径称为关键路径.多于一个直接前驱节点的节点称为关键节点.任务划分的主要思想是将关键节点划分到适合的队列中，生成最佳的任务调度队列，以提高任务的并行性.计算每个节点的平均完成时间(AECT)，根据AECT值对节点进行划分，然后在调度到合适的处理器上执行.划分优先队列时需要借助空队列Li(i=1，2，3…)，i的取值取决于实际入口节点的数量.参数Mexit(Li)表示队列Li出口节点的总数，Mpred(ti)表示节点ti的直接前驱节点的总数.对于多入口多出口节点的复杂任务应用程序，即存在多个入口节点和多个出口节点，可以采用零计算开销和零数据传输时间的节点作为伪入口节点和伪出口节点，伪节点不影响整个调度过程.

任务的平均完成时间(AECT)从入口节点开始采用递归的方式进行计算，其表达式如式(7)所示：

(7)

对于入口节点Tentry,其平均完成时间AECT表示为:

(8)

在优先队列划分的过程中，通过判断整个DAG任务图入口节点的数量，借助空队列Li，选择每个入口节点，放入空队列中单独成为一个队列.从入口节点开始递归计算每个节点的AECT值，队列中选择节点时按以下方式处理：

1)如果节点ti只有一个直接前驱节点，则直接将该节点放入其前驱节点的队列中；

2)如果节点ti有多个直接前驱节点，即Mpred(ti)>1时，则该节点为关键节点，比较其前驱节点的AECT值，将节点放入AECT值最大的节点队列中.

关键节点根据其前驱节点的AECT值来选择队列，将复杂度较高的任务图划分成低复杂度的队列，提高任务间的并行性.本文提出PQDSA算法的队列划分阶段伪代码如算法1所示.

算法1.队列划分算法

Queue dividing algorithm

Input：并行任务集G={T，E，W，C}

空队列Li(i=1，2，…，n)，n为入口节点的数量

Output：优先队列划分结果

1.从入口节点开始，向下遍历计算所有任务节点AECT值.

2.forti=t1totn

3.ifMpred(ti)==0

4. 借助空队列Li，将该节点放入空队列中

5.elseifMpred(ti)==1

6. 直接将给节点放入其前驱节点所在队列

7.else

8. 比较其直接前驱节点的AECT值

9. 将节点放入AECT值最大的节点所在队列

10.endif

11.endfor

任务划分队列结果如图3所示.

在算法1中，步骤1指从入口节点开始遍历每个节点，并计算每个节点的AECT值.步骤3-10实现节点根据队列划分条件选择优先队列，直至所有节点都在队列中.

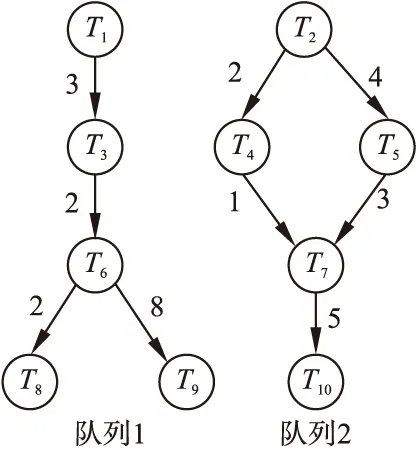
图3 任务优先队列划分结果Fig.3 Task priority queue division results

为了详细地说明队列的划分过程，图3所示为优先队列划分的实例化例子.由给定的DAG任务图2可知，图中有两个入口节点T1和T2，需要借助两个空队列L1和L2，将入口节点放入对应的空队列中，即L1={T1}、L2={T2}.图中节点T7有三个直接前驱节点，则该节点为关键节点，计算其直接前驱节点的AECT值，将节点T7加入AECT值最大的队列中，因此将T7加入队列L2中.初步得到队列L1和队列L2，最后检查生成的优先队列，队列L1存在两个出口节点T8和T9，则添加一个零计算开销和零通信开销的伪节点作为队列L1的唯一出口节点.最终划分得到的两个优先队列分别为L1={T1,T3,T6,T8,T9}、L2={T2,T4,T5,T7,T10}.

3.2 优先级选择阶段

由入口节点数量确定优先队列的数目，根据通信开销和平均计算开销将节点添加到队列中，从而提高任务间的并行性.由于关键节点的存在，队列间的数据依赖并没有完全消失.在确定任务集的调度顺序时，需要对队列中的所有任务节点计算TL(ti)值来确定任务的优先级.处理器对任务进行调度时，首先要考虑当前调度中是否存在关键节点任务，如果关键节点任务的前驱节点尚未调度，那么需要先调度其前驱节点再执行下一步.倘若该节点为关键节点，则表示该节点的直接前驱节点个数Mpred(ti)多于一个.倘若节点的直接前驱节点都来自同一队列，那么直接调度该关键节点.倘若其直接前驱节点有来自其他队列的节点任务，此时需要考虑该前驱节点是否已调度、数据是否已到达.在确定该前驱节点已经调度且数据已经到达之后，则该关键节点可以执行调度.对TL(ti)值相同的节点，可采取随机方式进行调度.

对于给定的DAG任务图2，根据入口节点划分两个优先队列的实例图如图3所示.在任务的优先级选择阶段，首先计算优先队列L1和L2中节点的TL(ti)值，然后将优先队列中节点根据TL(ti)值的大小按照升序排列，得到实例化优先队列L1和L2，对应的节点集合分别为{T1,T3,T6,T8,T9}、{T2,T4,T5,T7,T10}.

3.3 处理器选择阶段

通过对任务划分优先队列，很大程度上降低了任务的相关性，提高了队列的并行性，减少了节点的平均完成时间.再对队列中的任务进行优先级选择，生成任务的拓扑顺序，确保关键节点满足优先约束.这一节的重点是将任务调度到合适的处理器上执行，进一步提前节点的完成时间.在DAG任务图应用程序中，任务调度到某个处理器上执行，必须等待其所有前驱节点执行结束且相关数据到达其所在的处理器，该节点任务才可以开始执行调度.两个任务节点在同一个处理器上执行时，其通信开销为零.获取DAG任务图的关键节点，该关键节点在同层的节点中任务优先级最高.

任务实际开始时间(AST)和任务实际结束时间(AFT)的计算表达式为：

AST(tentry)=0

(9)

AST(ti)=AFT(ti)-wij

(10)

(11)

当ti与其前驱节点tj在同一处理器上执行，k=0；当ti与其前驱节点tj在不同处理器上执行时，k=1.

如果队列中任务都只有一个直接前驱节点，则可以将队列中所有任务分配到同一处理器，此时没有通信开销，也不需要等待其他节点的数据.如果任务直接前驱节点任务多于一个时，则该节点是关键节点，数据最后到达的前驱节点为关键父亲节点.

针对存在关键节点的任务队列，考虑到关键父亲节点数据到达的时间，不能直接把所有任务分配到同一台处理器上执行.本算法采用基于插入的思想，在处理器上足够大的时间槽空隙中插入任务.对于队列中非入口节点，但没有直接后继任务，可以将其单独放置于单独的处理器，给其他节点任务释放空间，进一步减少最终完成时间.PQDSA的全部伪代码如算法2所示.

算法2.PQDSA算法

PQDSA algorithm

Input：并行任务集G={T,E,W,C}，

空队列Li(i=1，2，…，n)，n为入口节点的数量

Output：DAG任务集的调度结果

1.从入口节点开始，向下遍历计算所有任务节点的AECT值.

2.forti=t1totn

3. 满足划分队列条件

4. 产生划分结果，队列L1，L2…

5.endfor

6.从每个队列的入口节点开始,向下遍历计算每个节点的TL(ti)值.

7.whileLi非空do

8. 按TL(ti)值升序排列

9.ifTL(ti)=TL(tj)

10. 随机排序

11. 生成优先级队列

12.endif

13.end

14.whileLi非空do

15. 队头节点ti从队列Li中出队

16.for处理器集合P中每个处理器

17. 计算AST(ti)和AFT(ti)

18. 为节点选择AFT(ti)值最小的处理器

19.endfor

20.end

3.4 PQDSA算法时间复杂度分析

在将n个任务调度到m个处理器上任务调度环境中，PQDSA主要包含优先队列划分、优先级选择和处理器选择三个部分，对这三个部分进行分析可得到算法总时间复杂度.

在优先队列划分阶段，DAG图中边之间的约束关系选择链表方式进行存储，该阶段的时间复杂度为O(n+p)，其中n为DAG图节点数量，p为处理器的数目.在优先级选择阶段，计算节点TL(ti)值，其时间复杂度为O(n2).最后在处理器选择阶段，计算节点调度到每个处理器上的AST(ti)值和AFT(ti)值，在将任务调度到AFT(ti)值最小的处理器上，其时间复杂度为O(n2×p).由此可知，PQDSA算法的时间复杂度为O(n2×p).

3.5 PQDSA算法调度实例分析

首先使用图2的实例化DAG任务图进行分析以及对比调度长度，然后在划分优先队列数量进行性能对比，以及节点数量不同和划分优先队列数不同的情况下，来进行实验比较分析.DAG实例化三个算法的调度长度对比图如图4所示.

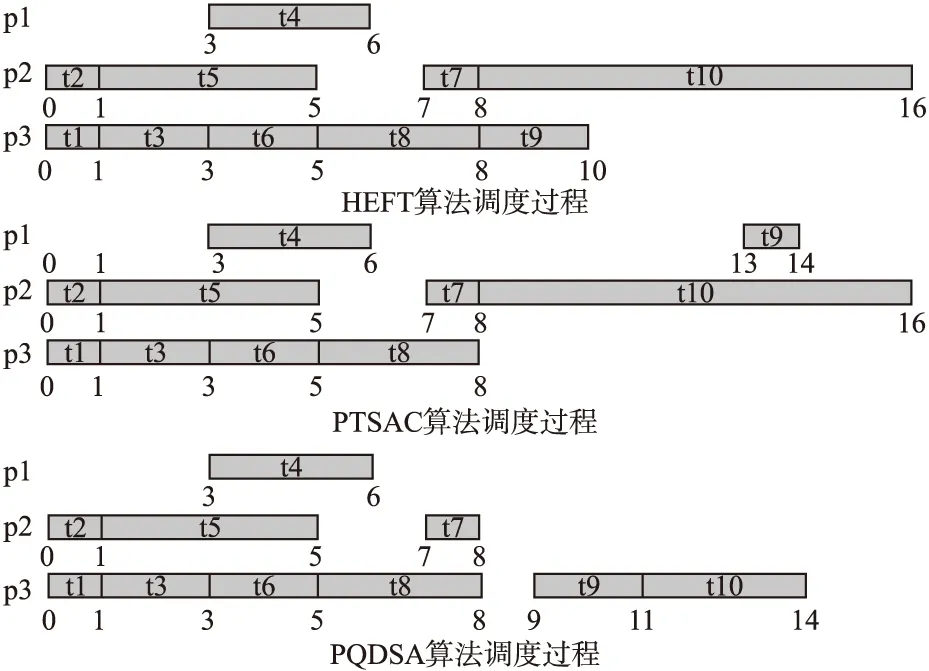
图4 三个算法的调度过程Fig.4 Scheduling process of three algorithms

针对图2给出的实例化DAG任务图，图4为HEFT算法、PTSAC算法和PQDSA算法的调度效果.HEFT算法对节点任务进行优先级排序，再采用基于插入策略将节点调度到处理器上.PTSAC算法通过通信开销和计算开销来确定相关性，判断是否进行复制.本文提出的算法PQDSA首先通过入口节点的数量来确定划分优先队列数，由图2可知，有T1和T2两个入口节点，因此可以划分两个优先队列L1和L2，将复杂多样的DAG任务图划分成两个相关性低的优先队列.然后按照节点划分队列的要求，将节点都放入到合适的队列中，如图3所示，生成最后的优先队列L1和L2.最后再将队列中的任务调度到处理器上.由图4可知，三个算法的调度长度分别为16、16和14，本文提出的算法的调度长度要比HEFT算法和PTSAC算法缩短了2个单位，相当于makespan降低了12.5%.

4 实验部分

4.1 实验环境

为了验证本文提出的PQDSA算法的可行性和有效性，以及避免因实验环境不同和对比的算法产生性能上的差异.本文采用相同的实验环境来进行对比.实验中使用Intel Core(TM)i5-9300H@ 2.40GHz四核处理器，16 GB内存，python版本为3.7，系统运行环境为Windows 10.

4.2 实验结果分析

本文主要采用调度长度(makespan)和调度效率(Efficiency)两个参数作为衡量算法的性能指标，并选取HEFT算法和PTSAC算法来进行实验对比分析.PQDSA算法的输入为DAG任务图，算法的输出为DAG任务图的调度结果.

4.2.1 任务调度长度

PQDSA算法主要侧重于任务调度长度，基于调度长度从两个方面进行实验.第一组实验是划分优先队列数不同时的调度长度比较，第二组实验是DAG节点数量不同时的调度长度比较，分别如图5、图6所示.图5分别为划分2、4、6、8、10个优先队列时3个算法的调度长度对比，图6为DAG节点数量分别为10、20、30、40、50时3个算法的对比情况.

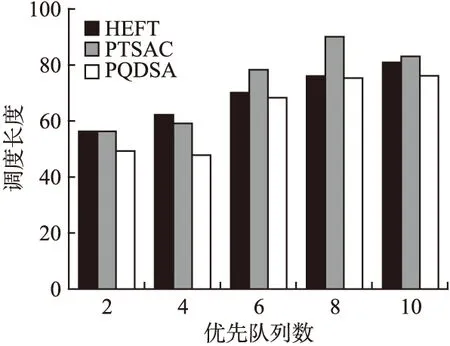
图5 划分队列数不同时三种算法调度长度对比Fig.5 Makespan comparison of three algorithms withdifferent queue numbers

图5的横坐标为划分优先队列数，是指由入口节点的数量来确定的优先队列数量，纵坐标为算法所需要的调度长度值.从实验数据对比可以得出，在任务调度时间长度方面，PQDSA算法的调度时间比HEFT算法和PTSAC算法要低，随着优先队列数的增加差距愈发明显.PQDSA算法根据入口节点对任务进行划分优先队列，将关键节点任务放入合适的队列中.在任务调度之前提高任务的并行性，降低节点间的时间消耗，随着优先队列数的增加，PQDSA算法的优势愈发显著.由实验数据可以得出，在划分优先队列数时调度长度方面，PQDSA算法比HEFT算法最高降低了22.5%，最低缩短了1.3%；PQDSA算法比PTSAC算法最高降低了18.6%，最低缩短了8.4%.

图6 不同DAG节点数量三种算法调度长度对比Fig.6 Makespan comparison of three algorithms withdifferent number of DAG nodes

图6中横坐标为DAG任务图的节点数量，纵坐标为调度长度.由图6的实验结果对比图可知，随着DAG中节点数量的增加，HEFT、PTSAC和PQDSA算法的调度长度变化并不明显.当节点数为10时，HEFT、PTSAC和PQDSA算法的调度长度差距并不明显；当节点数为20时，PQDSA算法的调度长度要明显低于HEFT和PTSAC算法.随着DAG中节点数量的增加，与HEFT和PTSAC相比，PQDSA算法在降低调度长度方面的优势愈发明显.当节点数为50时，PQDSA算法的调度长度要明显低于HEFT和PTSAC算法.当节点数量为10时，PQDSA算法只比HEFT算法和PTSAC算法降低了2个单位.节点数量为30时，PQDSA算法分别比HEFT算法和PTSAC算法缩短了3个单位和12个单位.当节点数量达到50时，PQDSA算法分别比HEFT算法和PTSAC算法减少了6个单位和7个单位.由实验数据不难得出，当DAG任务节点数量不同时，在任务调度长度方面，PQDSA算法要优于前两种算法.

4.2.2 调度效率

为了进一步验证PQDSA算法的性能，分别采用3种算法对DAG图进行调度，选择调度效率作为算法性能测试指标.针对优先队列数和DAG节点数量进行两组实验，实验结果分别如图7、图8所示.

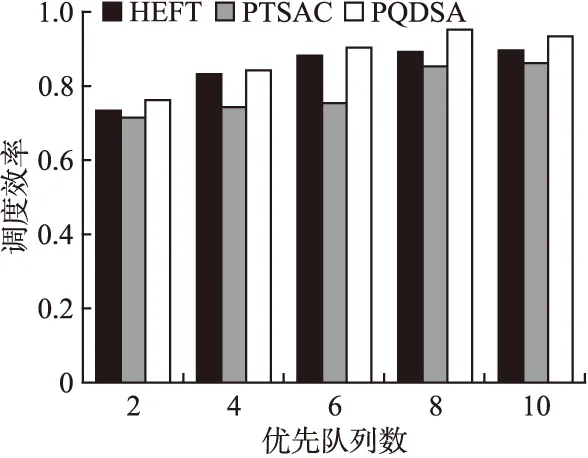
图7 划分队列数量不同时三种算法调度效率对比Fig.7 Comparison of scheduling efficiency of three algorithmswith different queue numbers

图8 不同DAG节点数量时三种算法调度效率对比Fig.8 Comparison of scheduling efficiency of three algorithmswith different number of DAG nodes

图7和图8的纵坐标均为算法的调度效率，图7的横坐标为划分优先队列数量，图8的横坐标为DAG节点数量.图7为优先队列数分别为2、4、6、8、10时的调度效率对比.图8展示了DAG中节点数量分别为10、20、30、40、50时的调度效率实验结果对比.由图7的实验数据对比分析可以得出，在算法调度效率方面，PQDSA算法都要优于HEFT和PTSAC算法.当划分的优先队列数分别为2、4、6时，PQDSA算法相对于HEFT算法提高并不明显，相对于PTSAC算法改善更为显著，尤其当优先队列为6时.当优先队列数达到8或者10时，PQDSA算法明显优于HEFT算法.因此，我们可以得出结论，PQDSA算法特别适合优先队列数较多的DAG图.由图7的实验数据对比可知，在划分优先队列数不同时，PQDSA算法在调度效率方面比HEFT算法最高提升了5.76%，最低增加了1.33%.比PTSAC算法最高提升了15.47%，最低增加了5.87%.由图8的实验数据可以得出，当DAG节点数量不同时，PQDSA算法在调度效率方面比HEFT算法最高提高了11.23%，最低改善了4.13%.比PTSAC算法最高提高了13.82%，最低增加了5.31%.由图7和图8的实验结果分析对比不难得出，PQDSA算法调度效率要优于对比的两种算法.其主要原因在于PQDSA算法采取划分优先队列的方法，将关键节点放置于合适的队列，再将任务分配到完成时间最小的处理器上，使得每一步都在降低任务的最晚完成时间.从整体上提高任务的并行性，减小任务的调度时间，提升任务的调度效率.

通过四组实验分析对比得出，PQDSA算法在调度长度以及算法的调度效率两个方面均优于HEFT算法和PTSAC算法.在任务调度长度方面最大分别降低了22.5%和18.6%，在调度效率方面最大分别提高了11.23%和15.47%.PQDSA算法在调度长度以及调度效率等方面，均呈现比较理想的效果.

5 总 结

云计算和人工智能的高速发展，边缘设备数量的剧增，这对高性能计算提出了更高的要求.异构环境下的任务调度问题是高性能计算中的研究重点.本文通过对DAG任务调度模型的研究，针对复杂多样的DAG任务图，本文提出一种基于优先队列划分的调度算法(PQDSA).PQDSA算法针对多入口多出口节点的任务图，根据入口节点采用划分优先队列的方法，将高复杂度、低并行性的节点任务划分成单独的队列.对于关键任务节点与其直接前驱节点存在依赖关系，划分队列时利用节点的平均完成时间将关键节点放入合适的队列，降低任务的时间消耗.实验结果的分析对比表明，PQDSA算法在调度长度和调度效率方面明显优于HEFT算法和PTSAC算法.