不规则线段树的差分隐私位置隐私保护方法

胡德敏，廖正佳

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1 引 言

差分隐私[1]作为位置扰动中一个常用的方法，具有严格的推理和证明的隐私保证，攻击者无论是否拥有背景知识[2]都无法推断出一条真实的位置数据，日渐成为位置保护中最受欢迎的方法.

基于差分隐私的位置保护方法会牺牲数据效用，用户在移动环境下连续查询时，单个位置点或兴趣点添加噪声后，会出现噪声叠加导致位置查询精度和服务质量下降等问题.树形结构的差分隐私[3,12]方法能拆分位置数据集以增强数据效用，并能在保护位置隐私的同时有效提高移动查询精度.但规则树形结构的差分隐私方法会造成大量无效零节点，数据结构过大，在查询精度上还有进一步提高的空间.

因此在规则树结构的差分隐私位置保护的基础上，提出了不规则树结构的差分隐私位置保护方法(Irregular Segment Tree Differential Privacy，ISTDP).该方法能有效解决差分隐私方法在移动环境下的连续查询精度下降的问题，并能适应不同密度环境.将k-匿名机制[4]与差分隐私相结合，引入线段树(Segment Tree)[5]的概念，形成匿名集后，使用不规则的线段树结构对数据进行划分；并将不规则线段树中节点覆盖率的差异加入对查询精度的考量，推导出衡量最优不规则线段树的估值函数；根据节点覆盖率构造子树的估值函数，从而得出较低的查询误差的线段树作为最终的不规则线段树；最后为每个节点分配具有较小误差上界的Laplace隐私预算.

2 相关工作

Dwork[1]最先提出的差分隐私方法，目标是对位置数据加入拉普拉斯噪声来模糊真实位置.现实中用户多是处于移动环境中进行位置查询，差分隐私方法免不了会使叠加的噪声量影响查询精度和数据的可用性.如何在隐私保护和查询精度之间获得较好的权衡，是研究者们一直努力的方向.

Hoa Ngo[6]提出了一种基于地理不可分辨性(差分隐私的广义变体)的隐私定义，通过发布多个版本的Hilbert曲线生成最小匿名区.该方法只是优化了匿名区，并没有改进差分隐私的噪声叠加问题.文献[7]主要思想是将数据转换成系数，将位置数据映射成小波树，然后添加拉普拉斯噪声，缺陷是映射成的小波树会产生大量无效节点，需要进一步压缩.在基于树结构的数据转换中，文献[8]提出了PLDP-TD算法，在底层轨迹数据库上构建一棵个性化的噪声轨迹树，并根据每个子轨迹分配一个隐私级，添加隐私参数，但规则的树结构造成数据结构过大算法效率低.文献[9]提出了kd-standard方法，在kd-树上进行了改进，利用差分隐私的指数机制和噪声均值机制，保证数据加噪后查询误差最小.但是这些的方法存在的共同问题是，使用树结构对数据进行转换时，需要将树映射成满n叉树的结构(如二叉树，四叉树等)，若兴趣点数据量不充足的情况下，会产生大量为零的节点，因此需要进一步压缩，才能保证查询误差较小，但是会造成算法复杂度较高.规则的树形结构会使数据结构较大无用节点较多，查询精度有进一步提高的空间.

本文以k-匿名机制为基础(利用Hilbert曲线[10]形成匿名集)，采用不规则线段树结构对数据进行优化.将不规则线段树中节点覆盖率的差异加入对查询精度的考量，根据节点覆盖率构造子树的估值函数，从而得出较低的查询误差的线段树作为最终的不规则线段树，最后为每个节点分配具有较小误差上界的Laplace隐私预算.提高了差分隐私的位置查询精度和服务质量，并能适应不同密度环境.

3 相关概念

3.1 差分隐私

定义1.ε-差分隐私[1].对于任何两个数据表T和T′，至多包含一个不同的记录，对任意输出S，S满足S⊆Range(f),随机函数f满足：

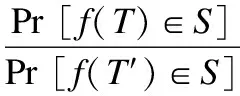
(1)

则称算法f满足ε-差分隐私.

差分隐私的定义规定了任意两个数据表经过差分扰动后，差异不超过给定的eε.对数据添加噪声主要由Laplace机制[1]实现.

(2)

满足Laplace分布的方差为2λ2，期望为0.由定义3可知，差分隐私的隐私强度与噪声参数λ有关，λ越大，噪声幅度越大，隐私保护强度就越高，但是数据可用性就越低.

定义3.Laplace机制的敏感度[1].敏感度是数据表T中任何单个元组数据变化时f中的最大变化.

(3)

根据Laplace机制的敏感度Δf、噪声参数λ、差分隐私参数ε，可以得出以下三者之间的关系：

3.2 线段树

定义5.线段树[5].线段树是一种二叉搜索树，给定一个数据集D，若满足以下条件的树，则称该树为D所对应的线段树：

2)令x的孩子节点为child(x)，对于孩子节点child(x)要满足：

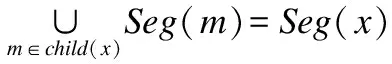
(4)

(5)

若child(x)为空集，则x为叶子节点.

对于普通加噪方式来说，为每条位置数据添加噪声后的敏感度Δf为1，由于查询会涉及到O(l)个数据，因此噪声方差和为O(lλ2).对于数据进行过基于线段树的划分后，线段树的深度为O(logl)，根据广义敏感度及其推理可知，深度为O(logl)的线段树的敏感度为Δf=O(logl).对于不规则线段树来说，设每个节点的扇出最大为d，因此噪声方差和为：

∑2λ2=O(2dloglλ2)=O(dloglλ2)

(6)

运用不规则线段树划分数据加噪后的噪声方差可以有效的减小误差，提高查询精度.

定义6[11].对于查询Q=[left,right]，要求满足一下条件的节点集合A：

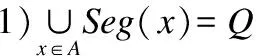
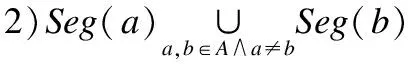
3)|A|最小

目的是要找到覆盖Q的查询区间且最少的不相交的节点.需要注意的是，对于覆盖节点x的查询Q=[left,right]，Q不能覆盖其父节点.

4 不规则线段树的差分隐私位置隐私保护方法

4.1 计算节点覆盖率

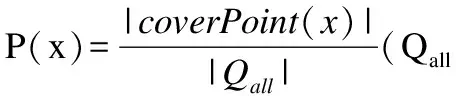
(7)

由于敏感度即为树高，则可以进一步将研究查询方差改为研究查询方差的期望，对于查询Q的方差的期望为：

(8)

利用Hilbert曲线划分出k-匿名集后，将匿名集映射成不规则树结构.如图1，用户在P9处形成的(k=3)匿名集的H值为<0,1,2,3,4>，将该H值进行线段树的转化后，该线段树的区间为[0,4]，长度为5.

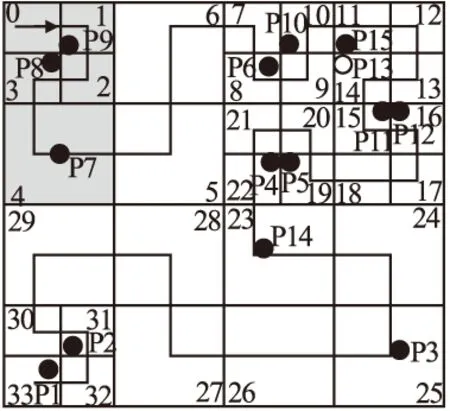
图1 Hilbert曲线形成的匿名集Fig.1 Anonymous sets formed by Hilbert curves

区间左端点不为1，因此，将区间往左移一个设为[1,5](离散化的值要从1开始).假设构造出的两种不规则线段树如图2所示，分别计算线段树节点的覆盖率：

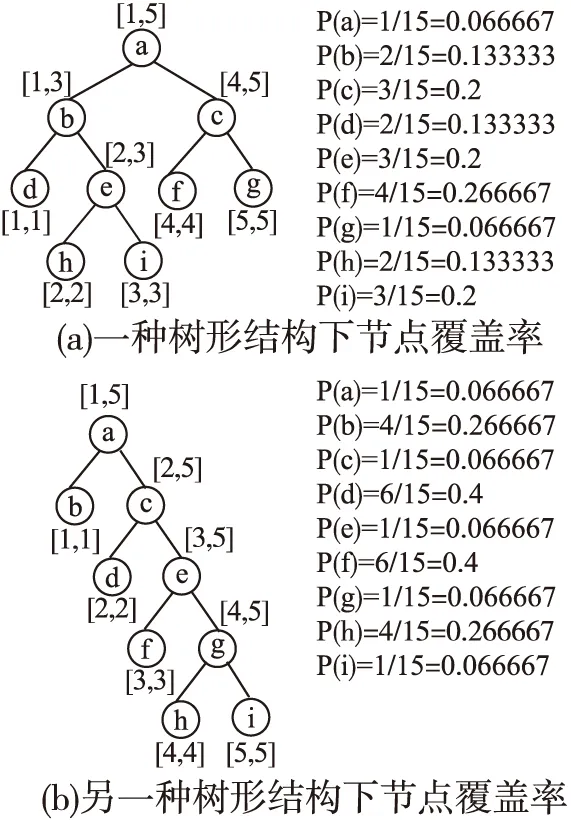
图2 线段树的节点覆盖率Fig.2 Node coverage rate of segment tree

4.2 不规则线段树的估值函数

根据定义6对线段树的查询覆盖区域的要求可知，根节点仅有一个查询区域能覆盖，即为该所在区域本身；对于非根节点x，其父节点为p，要求满足left(p)≤left(x)≤right(x)≤right(p)，由于查询区域Q=[left,right]不能覆盖父节点p，因此查询区域要求满足以下两个条件，见图3.

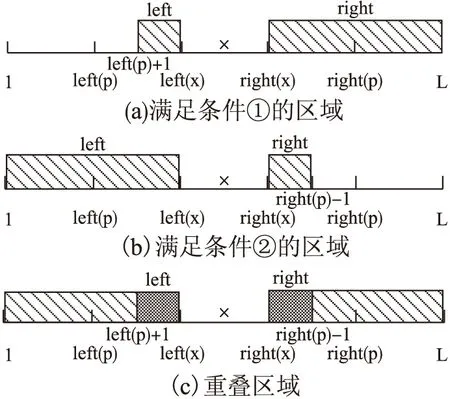
图3 节点查询区域区间Fig.3 Node query qrea section

P1(x)=

满足条件②的节点覆盖率为：

P2(x)=

满足条件的查询区间Q算了重叠的一段区间，如图3(c).重叠区域为(left(p)+1≤left≤left(x))∧(right(x)≤right≤right(p)-1)，该重叠区域的节点覆盖率为：

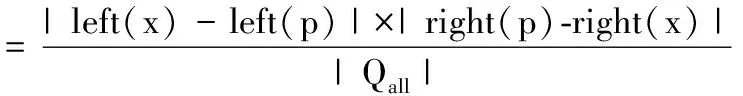
根据容斥定理，非根节点的节点覆盖率为P1(x)+P2(x)-P重(x).结合查询方差的期望，定义不规则线段树的估值函数为：

(9)

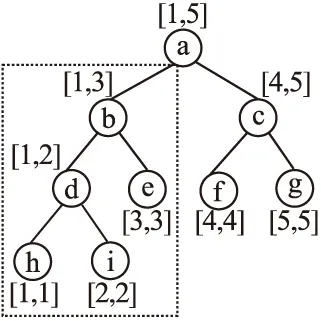
图4 节点b不同区间分布的线段树Fig.4 Segment tree with different section distribution of node b

此时节点b的估值函数为16.8，因此可以通过计算节点的估值函数，筛选出具有较低估值函数的线段树.不规则线段树的差分隐私位置保护方法的整体算法如下：

算法.不规则线段树的差分隐私位置保护算法

输入：生成的匿名区ASR，匿名集u.s

输出：扰动后的匿名区域ASR′

1. order(H(ASR.POI));//将匿名区ASR中单元格区域的H值按从小到大排序

2. find Hmax,Hmin in H(ASR.POI);//找到ASR中H值的最大值Hmax和最小值Hmin，形成查询区间[Hmin,Hmax]

3. if Hmin==0

4. Hmin =1,Hmax=Hmax+1;//若Hmin为0，将区间右移，变成[1,Hmax+1](保证左端点大于等于1)

5. end if;

6. if(left(x)！=right(x))//如果左端点不等于右端点，则递归划分子线段树

7. min=V(2,left(x),right(x));

8. m=2;//ary的值2 ary 20，先记录第一个值，接下来循环找出估值函数V(2,left(x),right(x))最小的子线段树

9. for(vari=3;i<=20;i++)

10. ary=i;

11. value=V(ary,left(x),right(x));

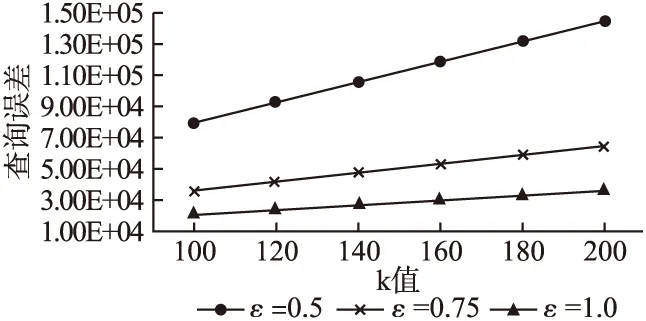
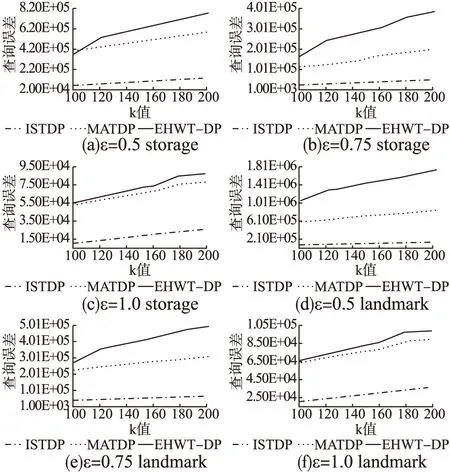
12. if(value

13. min=value;

14. m=ary;//记录下最优子线段树的扇出m

15. end if;

16. end for;

17. else break;//如果左右端点相同，则不用继续划分，该节点为叶子节点，否则重复步骤6-17

18. end if

5 实验结果与分析

将不规则线段树的差分隐私位置保护方法(ISTDP)、m叉平均树的差分隐私位置保护方法(MATDP)[12]以及对提高差分隐私查询精度有代表性的哈尔小波零树压缩算法(EHWT-DP)[7]进行对比实验.针对不同地理密度的环境、不同的总隐私预算ε、不同匿名集规模等条件下，主要从查询的误差(方差)、算法运行时间等方面评价算法的查询准确性以及算法运行效率.

5.1 实验数据与环境

实验环境为 Inter®CoreTMi5，windows7 操作系统，8GB 内存，算法是 Eclipse环境下基于Java 编写.本章实验使用了两个数据集进行对比：第一个是由infochimps大数据网站提供的美国48个大陆州的地标位置组成的地标，数据分布较密集，约有870k个数据点，实验中简称为“landmark”；第二个为美国存储设施位置数据，包括国家连锁存储设施，以及本地拥有和运营的设施，数据机较稀疏，约有9000个数据点的，简称“storage”.

实验中将查询方差的期望作为一项对误差的衡量标准，并且也将会与第三章中提出的m叉平均树的差分隐私方法进行对比，对比其查询误差的大小.实验中使用移动对象生成器，生成30km/h的300个移动用户，设查询总时间为 30min，查询间隔为 5min，因此所有用户一共要发起约1800次的连续查询.

5.2 不同隐私参数ε和匿名集规模下查询误差的变化

主要测试的是隐私参数ε对查询误差的影响，因此在实验中仅选择在storage数据集中测试(密度较高的数据集实验效果更明显)，分别取ε在0.5、0.75与1.0，匿名集规模k取100～200的情况下，观察ISTDP查询误差的变化，如图5.

图5 不同隐私参数ε和匿名集规模k下误差的变化Fig.5 Errors in differnet privacy parameters and anonymous set sizes

5.3 查询精度的对比

在该实验中，ε分别选取0.5、0.75、1.0三个值，针对两种不同地理环境的storage数据集与landmark数据集，测试ISTDP、MATDP与EHWT-DP三种算法的查询精度的对比，结果如图6.

图6 不同算法查询误差的对比Fig.6 Comparison of query errors between different algorithms

从图中可以看出，不论在哪种数据集下，本文的ISTDP方法的查询误差始终小于其他两种方法，且查询误差仅有其他方法的20%.整体看来ISTDP在不同数据集中的查询误差波动幅度不大，基本上呈现缓慢增长的趋势，这是由于分配的隐私预算具有最大的误差上界.MATDP和EHWT-DP两者受密度环境的影响较大，有的甚至有一个数量级的波动.可以得出结论，ISTDP比其他方法能更加不受地理环境密度分布的影响，且比其他减小查询误差的方法中查询精度更佳，误差较小，实验结果符合理论预期.

5.4 算法运行效率的比较

图7 算法运行时间Fig.7 Algorithm runtime

该实验在storage数据集和landmark数据集中进行，取匿名集规模k=120，隐私参数ε=1.0，对比ISTDP、MATDP和EHWT-DP三种方法的算法运行时间，如图7所示.

从图中可以看出，ISTDP与MATDP在两种数据集下的运行时间相差不大，这是因为这两种算法是基于树形结构的改进，仅与匿名集大小k有关，区域的网格划分和Hilbert曲线填充都是在离线环境下进行，所以运行时间相较于EHWT-DP方法少.ISTDP的运行效率并没有比MATDP提高多少，在ISTDP中主要时间复杂度是递归划分子线段树，所以该算法的时间复杂度为O(logk).ISTDP在MATDP的基础上没有对算法复杂度有大幅度的提高，但相比于EHWT-DP(时间复杂度为O(klogk))要提高了许多.

6 结束语

本文描述了不规则线段树的差分隐私位置保护方法，详细介绍了线段树的基本概念，将不规则线段树引入差分隐私方法中，能有效提高查询精度，减小连续查询时噪声叠加带来的查询精度下降的问题.实验验证了该方法对地理环境密度的影响较小，能适应不同密度环境的LBS位置查询服务，并且相对于其他提高差分隐私查询精度的方法有更小的查询误差.