一般间隙近似无重叠模式匹配
2020-05-09武优西闫文杰高雪冬
武优西,陈 彤,闫文杰,高雪冬
(河北工业大学 人工智能与数据科学学院,天津 300401) (河北省大数据重点实验室,天津 300401)
1 引 言
模式匹配(又称字符串匹配)是计算机科学的基础问题之一[1],其在生物信息学[2]、网络入侵[3]以及数据挖掘[4]等诸多领域具有重要应用,其问题实质是在一个相对长的序列串S上查找相对较短的模式P所有出现的位置及个数,这里序列串S以及模式P必须采用相同的字母表中[5].
近年来,为了满足实际需要,在传统通配符的基础上,研究者们致力于间隙约束的模式匹配,其模式串P可以表示为:P=p1[a1,b1]p2…[aj,bj]pj+1…[am-1,bm-1]pm(1≤j≤m),其中aj和bj分别为pj和pj+1之间通配符之间最小和最大通配符的个数.这种间隙约束的模式在序列模式挖掘中亦有深入探索,如Min等人[6]在间隙约束下探索了序列中字符作用不均等的模式挖掘方法;Wu等人[7]采用网树结构对周期性一般间隙的序列模式挖掘问题进行研究;Ding等人[8]在无重叠条件下探索了间隙约束的序列模式挖掘问题;文献[9]中提出免预设间隔约束的对比序列模式高效挖掘算法,解决了序列数据挖掘问题;Dong等人[10]在挖掘重复模式问题上,提出了e-RNSP算法;Tan等人[11]根据位置的频繁模式检测,提出具有弱通配符间隙算法.在上述研究中,均需采用间隙约束模式匹配技术实现模式支持度的计算,从而判定模式的频繁性,因此这种间隙约束模式匹配是序列模式挖掘的核心与基础[12].
当前研究主要在非负间隙下进行研究,即aj≥0,但一般间隙约束能得到更多有价值的信息.因此,Fredriksson和Grabowski[13]对一般间隙约束下模式匹配问题进行研究,柴等[14]也提出一般间隙及一次性条件的模式匹配问题,并提出了具有完备性的有效算法DNCP;文献[15]中提到一种基于灵活间隙模式匹配的服务器,并提出RNAPattMatch算法.与其他多种间隙约束模式匹配相比,无重叠模式匹配具有独特的计算性能[16],在序列模式挖掘中更容易发现有价值的频繁模式[17].
然而精确匹配有时不能完全提供给我们更多有价值的信息.在实际应用中大多数情况属于近似模式匹配[18].近似模式匹配问题是指在模式串中其中一个字符与序列串中某个字符进行匹配时,两个字符位置相同,但字符可以不完全相同.按照距离计算公式,可将近似条件约束模式匹配分为Hamming距离[19]、δ距离[20,21]及编辑距离[22]等.Hu等人[23]运用字符串相似搜索的通用Gram过滤器,提出了GFilter算法.
有鉴于此,本文提出了一般间隙近似无重叠模式匹配问题(Nonoverlapping Approximation Pattern Matching with General Gaps,简称NOAPMGG).该问题具有以下4个特点:它是一种严格的近似模式匹配问题,在匹配出现的过程中,不要求模式串上的字符与模式串上的字符完全相同;满足了无重叠条件约束,允许同一字符在多个位置使用多次,但不允许在同一位置上同一字符使用多次;在模式串的设定中,允许间隙设置上出现多个负间隙.
2 NOAPMGG问题
定义1(序列串).序列串记为S,S=s1…si…sn(1≤i≤n),由字符组成的长度为n的信息源,其中,si∈∑,∑表示为一种符号的集合.在不同应用当中,∑的意义也会随之不同.例如,在DNA基因序列中,∑由{A,C,G,T}组合而成.例如,S=s1s2s3s4s5=agcag,序列串S的长度为5.
定义2(模式串).模式串记为P,P=p1[a1,b1]p2…pj[aj,bj]pj+1…[am-1,bm-1]pm(1≤j≤m),其中,m指模式串P的长度,pj∈∑;aj、bj分别指间隙约束的下界与上界且取值必须是整数,并满足aj≤bj.若aj≥0且bj≥0,则称此区间为非负间隙条件约束;若aj或bj至少有一个小于0,则称此区间为一般间隙条件约束.
定义3(出现).出现记为L,如果一个位置索引L=
(1)
则称L为模式串P在序列串S上的一个出现.例如,模式串P=p1[a1,b1]p2[a2,b2]p3= A[0,3]T[0,2]C,则说明模式串P的长度为3;在字符A和字符T间根据间隙约束可知,两个字符间可通配0到3个字符;而字符T和字符C间根据间隙约束可知,两个字符间可通配0到2个字符.
定义5(Hamming距离).Hamming距离记为T,即表示两个(相同长度)字对应位不同的数量.例如:序列串S1=s1s2s3s4s5=abcab与序列串S2=s1s2s3s4s5=acbac,在两个序列串中,第2、3、5位置字符不同,因此,Hamming距离为3.
3 网树与NOPARLA算法
3.1 网树的概念
网树的数据结构是一种树型结构的拓展,目前被应用于解决多种模式匹配问题[24]、序列模式挖掘问题[25]和图问题[26],其定义如下:
定义6(网树).网树是一种非线性数据结构,是由根结点与子网树组成,所有相连的路径之间用来表示双亲与孩子关系.
性质1.网树具有树结构的一些特点,如双亲、孩子、叶子结点、根结点、层等.此外,其具有如下独特特点:
1)一棵网树中可以存在一个或多个根结点;
2)网树中非树根结点也会存在多个双亲结点;
3)任何一个结点到它的祖先结点路径可能不止一条;
4)给定序列中的结点可以在网树的不同层上出现;
5)一个结点的孩子结点一定在网树的同一层上出现.
定义7(树根叶子路径).在网树中,能从树根结点到叶子结点的一条完整的路径.
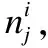
定义9(最右双亲策略).从最后一层的最大结点开始查找,选择最右双亲结点向树根方向寻找树根的过程.首先判断最右双亲结点是否满足间隙约束条件,若满足则进行匹配,若不满足则判断次右双亲结点,直至找到相匹配的双亲结点.
定义10(最左孩子策略).从第一层的最小树根结点出发,选择最左孩子结点向叶子结点方向寻找路径的过程.首先判断最左孩子结点是否满足间隙约束,若满足则进行匹配,若不满足则判断次左孩子结点,直至找到与之相匹配的叶子结点.
3.2 NOPARLA算法的设计及分析
3.2.1 创建一般间隙近似网树
在文献[16]中,提出利用网树的结构特点可以有效地解决无重叠条件约束下的模式匹配问题.由于本文研究的是近似距离下的模式匹配问题,因此需要在文献[16]的创建网树问题上进行一些修改.在修改算法的过程中会存在两个难点:在处理结点关系时,会出现Hamming距离的实时更新;在创建父子关系前,需要进行预判断处理.
在创建一般间隙近似网树前,我们需提到一些与近似距离相关的定义如下.
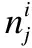
1)计算该叶子结点到根结点之间的Hamming距离d时树根到叶子的路径数;
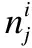
(2)
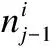
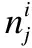
1)计算该根结点到叶子结点之间的Hamming距离d的路径数.
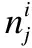
(3)
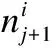
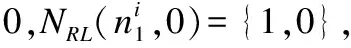
算法1.CreateNetTree
输入:长度为m的模式串P,长度为n的序列串S,Hamming距离阈值T
输出:网树NetTree
1.forj=1 tomstep 1do
2.fori=1 tonstep 1do
3. 依据定义11创建并计算结点的NHDRL值;
4.endfor
5.endfor
6.returnNetTree;
例1.给定序列串S=tgttagt,模式串P= t[-1,1]t[-1,2]a[-1,1]t,Hamming距离为1,根据CreateNetTree算法可以建立一棵近似网树,如图1所示.
该网树的创建步骤如下:
1)当j=1时,将序列串中所有字符一次扫描插入第一层nettree[1],根据定义13,对所有结点进行初始值定义;

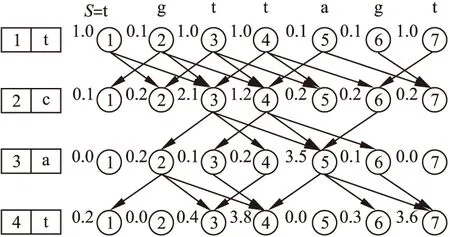
图1 模式串P在序列串S对应的网树Fig.1 Nettree for pattern P in sequence S
3.2.2 最左孩子策略
为解决近似距离阈值问题,在创建一般间隙近似网树为每个结点都进行了在不同Hamming距离下路径数量的定义与计算.若满足近似度阈值条件,则根据树根叶子路径数匹配该结点的孩子结点.该方法可以有效提高匹配效率,具体过程如下:从最小根结点出发,根据间隙约束条件与Hamming距离的设定,当上一层结点与下一层结点建立关系时,根据公式(2)选择与之匹配的最小孩子结点.其算法如算法2.
算法2.RootToLeaf
输入:NetTree,模式串P长度为m,序列串S长度为n,阈值T,当前结点F
输出:occin,各层结点F[m]集合
1.occin.position[1]=t;
2.F[1]=nettree[1][t];
3.ifF[1].used=true orF[1].toleave=falsethen
4.ifp[1].start≠s[F[1]]thenapprox=1;
5.forj=1 tomstep 1do
6.fort=1 tonettree[j][i].children.size()step 1do
7.maxh=T-approx;
8.endfor
9.ifnettree[j][child].toleave=false thenapprox=
approx+1;
10.endfor
11.endif
12.returnoccinandF[m];
3.2.3 近似阈值监测机制
根据文献[17]可知,基于从最小根结点向下采用最左孩子结点找到较多的树根叶子路径,若模式串P的间隙约束略大或间隙条件过多时,结点的孩子结点也会成倍增加,由于近似度阈值的约束会造成该结点选择的孩子结点并不是最小孩子结点,因此仅依靠最左孩子策略并不能找到更多的出现,由此可见需要引入近似阈值检测机制.具体过程如下:从网树的第二层开始,若第一次检测到si=pj,且该结点在Hamming距离0~T-1时有路径,则重新向上根据最左双亲策略寻找与之匹配的结点.其算法如算法3.
算法3.RootToLeaf_Approx
输入:NetTree,模式串P(长度:m),序列串S(长度:n),阈值T,当前结点Q
输出:occin,各层结点Q[t]集合
1.forj=1 tomstep 1do
2.if(j≤m)then
3. 采用算法2,从结点Q[t]出发,采用最左孩子策略,获得子路径Q及对应的Hamming距离为approx的子模式;
4.forx=jdownto 2 step-1do
5.fory=1 toNetTree[x][y].parents.size()step 1do
6.maxh=T-approx;
7.endfor
8.ifNetTree[x][child].toleave=falsethenapprox=approx+1;
9.endfor
10.endif
11.endfor
12.returnoccinandQ[t];
3.2.4 剪枝策略
定理1.若同一网树中有互不相交的两条路径分别为A、B,则A、B经过的路径上所有结点可构成两个无重叠出现.
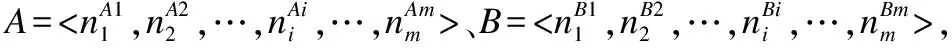
由定理1可知,同一棵网树中有两条互不相交的两条路径,可构成两个无重叠出现.因此,根据最左孩子策略,在网树上剪掉一条树根叶子路径后,并不会影响寻找其他的无重叠出现.但在进行剪枝后会出现一些不能到达叶子结点的结点,只需从叶子到树根逐层检测,将不可抵达叶子结点的结点进行剪枝,这样可避免回溯过程.其算法如算法4.
算法4.Pruning
输入:NetTree,模式串P的长度m,occin
输出:NetTree
1.fori=mdownto 1 step-1do
2.position=occin.position[i];
3.ifi 4.pos=occin.position[i+1]; 5.position_b=NetTree[m+1][pos].parent[0]; 6.ifposition_b 7.endif 8.forposition=1 toNetTree[i].size()step 1do 9.current=NetTree[i][position]; 10.ifcurrent.used=false ¤t.child=false thenbreak; 11. updatecurrent.used; 12.ifcurrent.used=truethenupdate NHDRL; 13.endif 14.endfor 15.endfor 16.returnNetTree; 3.2.5 求解算法NOPARLA算法 根据本文提出的问题,NOPARLA算法将作为求解算法.该算法原理: 1)根据算法1将问题转化成一棵网树并根据性质11和公式(2)对结点进行NHDRL值定义; 2)从下往上根据性质12和公式(3)对结点进行NHDLR值定义; 3)采用算法3进行最左孩子策略和近似监测机制; 4)当找到一个无重叠出现时,采用算法4将网树进行剪枝; 5)重复第3、4步,直至找到所有无重叠出现. 其算法如算法5: 算法5.NOPARLA 输入:长度为m的模式串P,长度为n的序列串S,阈值T 输出:符合条件的无重叠出现集合C 1. 采用算法1创建一棵近似网树NetTree; 2.forj=m-1 downto 1 step-1do 3.fori=1 tonstep 1do 4. update NHDLR; 5.endfor 6.endfor 7.fort=1 toNetTree[1].size()step 1do 8. 采用算法3 RootToLeaf_Approx(N,Q[t]),从结点Q出发,采用最左孩子策略; 9. 采用算法4 Pruning更新NetTree; 10.C=Q∪occin; 11.endfor 12.returnC; 例2.给定序列串S=tgttagt和模式串P= t[-1,1]t[-1,1]a[-1,2]t,Hamming距离为1. 计算过程如下: 1)模式串P在序列串S中所建立的对应网树,如图1所示. 2)根据公式(3)对网树重新定义NHDLR值. 根据NOPARLA算法,可以找到三个无重叠出现,即<1,3,2,1>、<3,4,3,4>、<4,6,5,7>. 由于网树最多只有m层,每一层结点数最多只有n个结点,由此可见,每一个孩子结点最多会有W个双亲结点,即W=max(bj-aj+1),且aj为间隙约束的下界,bj为间隙约束的上界,近似阈值为T.因此,NOPARLA算法的空间复杂度为O(m*n*W*T).其中,m为模式串的长度,n为序列串的长度,W为模式串的最大间隙长度W=max(bj-aj+1),T为近似阈值. 在分析本文算法时间复杂度之前,先分析CreateNetTree算法、RootToLeaf算法、RootToLeaf_Approx算法以及Pruning算法的时间复杂度.易知CreateNetTree算法创建一棵一般间隙近似网树的时间复杂度为O(m*n*W*T);在RootToLeaf算法中,每个结点最多有W个孩子结点,网树共有m层,近似阈值为T,所以RootToLeaf算法的时间复杂度为O(m*W*T);RootToLeaf_Approx算法的时间复杂度为O(m2*W*T);根据Pruning算法可知,该算法的时间复杂度为O(m3*W*T).由于NOPARLA算法最多运行n-m次剪枝算法,由此本文算法的时间复杂度为O(m3*n*W*T). 本文中实验运行的软、硬件环境为:Inter(R)Core(TM)i5-3210处理器、2.50GHz主频、4.00GB内存、Windows8.1 专业版操作系统的计算机.完成实验工具为Microsoft Visual C++6.0.本文所使用的测试序列串均为真实的生物数据,DNA序列均来自美国国家生物计算信息中心网站1.为体现模式串的间隙约束具有一般性规律,在本文中设计了九个具有一般性的模式串. 表1和表2分别给出了实验中使用的序列串和模式串的特征. 表1 真实生物序列 序号片段名称位点片段长度S1Segment 1CY0585632286S2Segment 2CY0585622299S3Segment 3CY0585612169S4Segment 4CY0585561720S5Segment 5CY0585591516S6Segment 6CY0585581418S7Segment 7CY058557982S8Segment 8CY058560844 为了测试本文NOPARLA算法的性能,我们又提出了三种对比算法,即NOPALR算法、NOPARL算法和NOPALRA算法.这三种对比算法均采用网树结构进行求解,其中NOPALR算法采用最右双亲策略,当找到一个无重叠出现时将网树进行剪枝;NOPARL算法采用最左孩子策略,当找到一个无重叠出现时将网树进行剪枝;NOPALRA算法采用最右双亲策略,再采用近似阈值检测,当找到一个无重叠出现时将网树进行剪枝. 本文选取表2中P1~P9中的9个模式串与表1中S1~S8中的8个序列串作为本文的对比实验数据,在选取近似阈值T=1与T=2进行对比实验,并对这四种算法的求解质量与求解速度进行对比.表3和表4分别给出了近似阈值T=1与T=2情况下,模式串P1~P9在序列串S1~S8上的出现总数. 表2 模式串 表3T=1时,序列S1~S8在模式P1~P9上的出现总数 出现数P1P2P3P4P5P6P7P8P9NOPALR341045303193255514581725123027493199NOPARL353244143452268818821905161629303218NOPARLA351843573382273016791882140030943450NOPARLA360345563445265819722016169331473508 表4T=2时,序列S1~S8在模式P1~P9上的出现总数 出现数P1P2P3P4P5P6P7P8P9NOPALR6468100866216499126192500211843604469NOPARL6575101236389533826012524227143604445NOPARLA6438101126220520427662713226846684828NOPARLA6664101976442508727882753240548044971 为了能更清晰的反映出四种算法分别在近似阈值T=1与T=2情况下,模式串P1~P9在序列串S1~S8上的时间性能,四种算法的平均运行时间见表5和表6. 1)在求解性能方面,NOPARLA算法整体比NOPARL算法、NOPALR算法与NOPALRA算法较好. 通过表3~表4,即T=1和T=2时,序列串S1~S8在模式P1~P9上的出现总数.从两张表中,清晰看出NOPARLA算法从总体来说,求解性能优于其他三种算法.在模式串P3上,NOPARL算法求解性能优于NOPARLA算法;在模式串P4上,NOPALRA算法与NOPARLA算法均没有NOPARL算法的求解性能好;产生这样的原因一是由于序列串的长短会造成这样的原因,由于在NOPARL算法与NOPALR算法并没有判断近似监测机制,因此,对网树造成较小的影响;二是因为当序列串足够长的时候,为了能找到能多有价值的出现,算法对近似距离做检测,当满足一定条件时,会触发近似监测机制,使得产生的新无重叠出现比原有无重叠出现对网树的影响减小,因而提高了算法的求解性能. 表5T=1时,序列S1~S8在模式P1~P9上的平均运行时间 平均时间P1P2P3P4P5P6P7P8P9NOPALR4392844394141164171714579301424NOPARL52235052548814332145176711331660NOPARLA50634052548613522029168410781625NOPARLA53937354351014812271183411491735 表6T=2时,序列S1~S8在模式P1~P9上的平均运行时间 平均时间P1P2P3P4P5P6P7P8P9NOPALR74041277955128116184369120244986NOPARL83846790877731316840409422405250NOPARLA77143880361130686908410222425521NOPARLA86449493477232747387429523855855 2)在求解性能方面,通常情况下NOPARLA算法比NOPALRA算法可以发现更多的出现. 从表3~表4可以看出,在模式串P1~P9上,当T=1时,NOPARLA算法有七次获得了最多出现数,当T=2时,NOPARLA算法有八次获得了最多出现数. 3)在时间运行方面,改进后的NOPARLA算法与NOPALRA算法运行时间总体比未改进的NOPARL算法与NOPALR算法较长. 从表5~表6可以看出,即T=1和T=2时,序列串S1~S8在模式P1~P9上的平均运行时间下,NOPARLA算法在运行时间上总体来说消耗最多,NOPALR算法消耗的时间最少,并且可以看出NOPARLA算法与NOPALRA算法消耗的时间,从整体来说均比NOPARL算法与NOPALR算法时间长,造成这种现象别的主要原因是在处理无重叠出现时,对近似距离做检测,通过检测可以找到更多有价值的出现,因此会增加时间的运行. 4)随着近似阈值T的增加,找到的出现数与运行时间也会随之增加. 通过表3~表4,即T=1和T=2时,序列串S1~S8在模式P1~P9上的出现总数.换言之,当T从0到2逐渐增大时,出现数也会随之增加,产生这样现象的原因是由于近似阈值T可转换为近似距离为T-approx及近似距离为approx问题.从表5~表6可以看出,即T=1、T=2时,序列串S1~S8在模式串P1~P9上的平均运行时间也会随之增加,这与上一章中提高的算法时间复杂度与空间复杂度分析一致. 通过本章做的大量实验进行分析可知,与其他3种算法相比,NOPARLA算法从整体来说性能最好. 本文提出了一般间隙近似无重叠模式匹配问题,即NOAPMGG问题.该问题需要满足无重叠模式的条件约束,为增加模式串的一般性而提出近似模式匹配,为进一步增加模式串的灵活性而提出一般间隙模式匹配问题,来解决NOAPMGG问题.本文提出NOPARLA算法,该算法根据网树的结构特点,采用最左孩子策略,使用近似阈值机制找到一个无重叠出现.该算法的空间复杂度与时间复杂度分别为O(m*n*W*T)和O(m3*n*W*T),其中m为模式串的长度,n为序列串的长度,W为模式串的最大间隙长度,T为近似阈值.通过大量实验证明了,NOPARLA算法具有较高的可行性与高效性.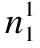
3.3 算法分析
4 实验结果及分析
4.1 实验环境及实验数据
Table 1 Sequences of real biological data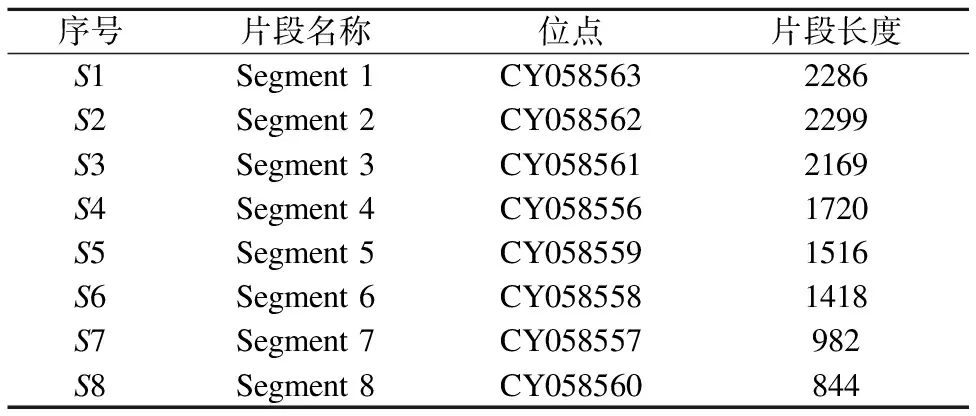
4.2 实验结果
Table 2 Patterns
Table 3 Total results ofS1~S8 inP1~P9 whenT=1
Table 4 Total results ofS1~S8 inP1~P9 whenT=2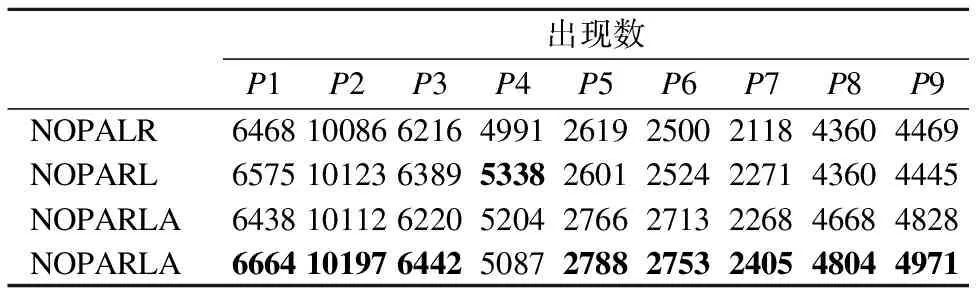
4.3 实验结果分析
Table 5 Average running time ofS1~S8 inP1~P9 whenT=1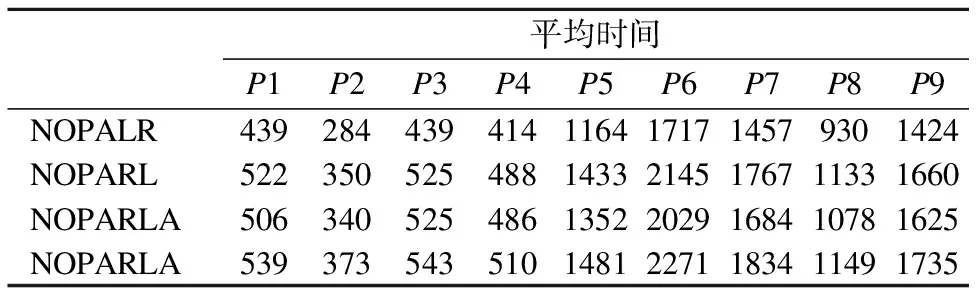
Table 6 Average running time ofS1~S8 inP1~P9 whenT=2
5 结 论
