云环境下基于强化学习的多目标任务调度算法

童 钊，邓小妹，陈洪剑，梅 晶，叶 锋

(湖南师范大学 信息科学与工程学院，长沙 410012)(高性能计算与随机信息处理省部共建教育部重点实验室(湖南师范大学)，长沙 410012)

1 引 言

随着计算机科学和互联网技术的快速发展，云计算作为一种新的并行与分布式计算技术的发展方向被提出来[1].云计算平台上的所有数据计算和存储都在云端进行，可以通过使用最少的代价来充分利用互联网上的资源，以实现资源利用率最大化的目的[2].通常，根据用户所需要的服务模式的不同，云计算可以分为三种类型：基础设施即服务(IaaS)、平台即服务(PaaS)和软件即服务(SaaS)[3].在云计算平台上，如何将用户提交的请求合理的分配给云计算节点进行处理，是影响云用户的服务体验和云服务提供商的利润率的重要因素，也是任务调度要解决的核心问题.云计算中的任务调度是一个NP难问题，根据所要解决的云用户需求的不同，任务调度算法往往侧重于不同的优化目标，主要包括：调度长度(makespan)、负载均衡(load balance)、服务质量(Quality of Service,QoS)和经济原则(economical principle)等[4].

目前，大多数对于任务调度的研究只侧重了对单目标问题的优化，对于多目标调度问题由于其复杂性，研究相对较少.但在现实问题中，只做到对任务调度问题进行单目标的优化通常是不够的，多数情况下需要同时考量云用户的用户体验和云服务提供商的消耗成本等多方面的因素进行决策.因此，本文考虑同时对任务的完成时间和虚拟机的执行成本这两个有重要意义并且相互冲突的目标进行优化，拟解决在满足云用户对减少makespan的需求的基础上，同时保证对云服务提供商的成本消耗的控制.

针对云环境下的任务调度算法的研究，Topcuouglu等[5]提出了优化makespan的异构最早完成时间(Heterogeneous Earliest Finish Time,HEFT)算法.HEFT算法在小规模的有向无环图(Directed Acyclic Graph,DAG)上可以得到较好的性能，但是随着任务规模的增大，DAG任务的复杂性增加，导致HEFT算法的性能随之下降；并且该算法只考虑了对单目标makespan的优化，没有考虑其他影响任务调度性能的因素，使得该算法在实际应用当中具有一定的局限性.李君等[6]提出一种综合时间能耗成本的任务调度算法(Time and Energy Consumption Cost Scheduling,TECCS)，通过引入通信因子和计算因子综合时间与能耗成本来决定任务的调度顺序，在期望完成时间条件下节省更多任务执行成本；但是该算法考虑的是在期望完成时间的条件下实现对能耗成本的优化，没有实现对双目标的同时优化.可以得知，传统的任务调度算法存在着对不同的任务类型适应度低、搜索时间长以及容易陷入局部最优解等不足.

目前，机器学习已经开始被用于有效的解决任务调度这类组合优化问题[7-9].机器学习的研究最早从Samuel发明的下棋程序开始，发展至今已经被广泛用于解决诸多领域的研究问题，是指机器通过学习数据的内在信息，获得自身的经验信息来指导其完成智能行为[10].强化学习(Reinforcement Learning,RL)是建立在马尔科夫决策过程(Markov Decision Process,MDP)上的一种重要的机器学习算法，它是指在无外界监督指导的情况下通过与不确定的外部环境进行交互，从而获得最优解的一种学习过程[11,12].经典的RL算法包括Q-learning、SARSA和策略梯度(Policy Gradients)，其中，Q-learning算法在解决任务调度问题上具有较好的效果.Q-learning算法是指通过引入期望延迟反馈来解决无完整信息的MDP问题的一种方法，它不需要提前获取环境模型，主体(Agent)是Q-learning中的一个重要组成元素，它可以根据历史经验来学习并且选择一个最优的动作，最终被选择的一系列动作组成一个最优策略[13].

Siar等[14]提出了一种将RL和智能技术结合的方法用于解决并行系统中的任务调度问题，Agent通过Q-learning方法来学习如何将效率最大化，并且使用一种新的协作Q-learning算法来促进Agent之间的交互，从而提高整个系统的效率.Cui 等[15]提出一种新的基于Q-learning的任务调度算法，在一定数量的虚拟机资源下最小化makespan和平均等待时间.Wei等[16]提出一种基于Q-learning和共享值函数的任务调度算法，以解决现有合作学习算法中信息频繁交换的问题，该算法设计了任务模型和Q-learning模型，在约束条件下降低了协作信息的切换频率，具有良好的学习效果.

本文针对HEFT算法只适合解决小规模DAG任务的调度问题以及只考虑了对单目标makespan的优化，提出一种基于Q-learning的多目标任务调度算法(Multi-objective Task Scheduling Algorithm based onQ-learning，QMTS).在QMTS算法中，首先利用Q-learning算法指导任务进行优先级排序，其中使用HEFT算法的Upward Rank值(式(9))作为Q-learning更新过程中的立即奖励值，可以得到比HEFT算法更小的makespan；其次针对HEFT算法在处理机分配阶段只考虑将任务的最早完成时间作为影响分配的因素，从而导致云服务提供商的消耗成本没有得到有效的控制.本文使用线性加权法将最早完成时间和消耗成本综合考虑作为虚拟机的分配依据.实验结果表明，本文所提出的QMTS算法得到了比HEFT及其他经典的调度算法更好的多目标优化结果.

2 问题描述

2.1 云任务调度问题

虚拟化是云计算中的核心，云计算平台上的每个计算节点代表了具有不同处理能力的虚拟机，定义如下：

V={V1,V2,…,Vm}

(1)

在本文中，拟实现在云计算环境下任务之间有依赖关系的多目标静态任务调度算法，有依赖关系的任务类型通常使用DAG任务来表示，定义如下：

G=(T,E,C,W)

(2)

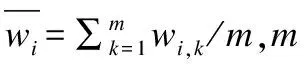
一个简单的DAG任务模型如图1所示，图中共有8个任务节点，每个任务节点由两个部分组成：任务节点编号和该任务在所有虚拟机上的平均计算时间.任务图中有向边上的数值代表两个任务之间的通信时间.

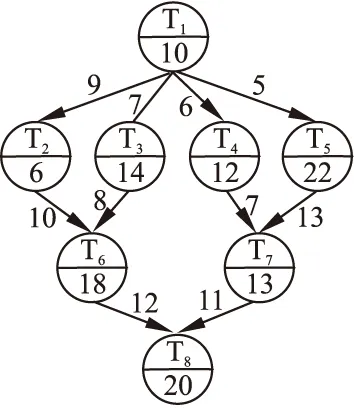
图1 一个8个任务的简单DAG模型Fig.1 A simple DAG model with 8 tasks

2.2 优化目标模型

在本文中，拟实现同时减少任务的makespan和虚拟机消耗总成本的多目标任务调度算法(QMTS).

2.2.1 makespan模型

在云环境下任务调度问题的研究中，makespan一直是一个重要的评价指标.对于给定的任务集合，最后一个任务的完成时间即为整个任务调度的makespan结果.任务Ti在虚拟机Vk上的最早开始执行时间定义为：

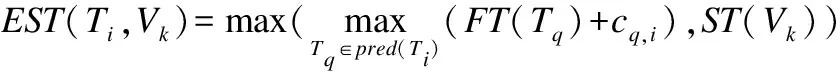
(3)

其中：pred(Ti)是任务Ti的所有直接前驱任务节点的集合，FT(Tq)是任务Tq的完成时间；ST(Vk)是虚拟机Vk最早可开始执行任务Ti的时间.根据定义，DAG任务中入口任务的最早开始执行时间为0.

任务Ti在虚拟机Vk上的最早完成时间定义为：

EFT(Ti,Vk)=wi,k+EST(Ti,Vk)

(4)

可以得知，最后一个任务的最早完成时间即为整个DAG任务调度的makespan，表示为：

(5)

2.2.2 总成本模型

总成本(total cost)是指完成所有任务之后，在所有虚拟机上所耗费成本的总和.定义如下：

(6)

其中：pricek是虚拟机Vk在计算单位时长的任务上的执行费用.通常，计算速度越快的虚拟机所需的单位执行费用越高；timek是分配到虚拟机Vk上的任务的总执行时长.对于pricek的定义有多种方式，如线性定价方式和指数定价方式[17]，本文给出一种定价方式如下所示：

(7)

式(7)的推导思路为：首先给出不同计算速度的虚拟机之间的单位执行费用的线性关系为pricek=priceh×(sk/sh),k=h+1≤m，这里将所有虚拟机按照计算速度从小到大进行排序，priceh是虚拟机Vh的单位执行费用，sk和sh分别是虚拟机Vk和Vh的计算速度；其次由于在线性关系中不同虚拟机处理相同的任务实际上消耗的成本是相同的，因此引入相关的函数来解决这个问题；最后考虑到在指数定价方式中虚拟机的计算速度加快时，其单位执行费用的增长过快.于是引入对数函数来避开现有的两种定价方式的不足，由于虚拟机Vk的计算速度大于Vh，因此(sk/sh)>1，得到ln(sk/sh)>0，即1+ln(sk/sh)>1，使得虚拟机价格增加速度与对数函数相似，更符合实际生活中的定价模式.由此可知，单个任务Ti在虚拟机Vk上的执行成本表示为：costTi=wi,k×pricek.

2.2.3 优化目标函数

本文提出的算法试图对makespan和总成本(total cost)同时进行优化，可将目标函数定义为：

min:{makespan,totalcost}
s.t.makespan≤makespanmin
totalcost≤totalcostmin

(8)

其中，makespanmin和totalcostmin分别是在本文其他3种对比算法中产生的最小的makespan结果和最小的总成本结果.

3 多目标调度算法设计

本章结合HEFT算法与Q-learning算法提出了同时实现最小化makespan和总成本的多目标任务调度算法QMTS，达到用户体验最优和云服务提供商总成本最小的目的.

3.1 HEFT算法

HEFT是静态DAG任务调度中的经典算法之一，对于减少整个任务执行过程的makespan有着较好的表现.算法在任务排序阶段，使用Upward Rank值(式(9))作为任务优先级值，充分考虑到了任务的计算时间、任务间的通信时间以及子任务的优先级对父任务优先级的影响；在分配处理机阶段，HEFT算法使用最早完成时间策略(式(4))，即将每个任务都分配到能使其最早完成的处理机上执行.

Upward Rank值的定义如下所示：

(9)

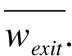
HEFT算法的执行过程如图2所示.

图2 HEFT算法流程图Fig.2 Flow chart of the HEFT algorithm

HEFT算法虽然在任务排序和处理机分配阶段都有着较充分的考虑，但是由于其只依据Upward Rank值进行了一次性的排序，导致在任务节点多且结构较复杂的DAG任务上往往得不到合理的任务执行顺序，以至于在产生最优makespan上的性能下降；并且在处理机分配阶段只考虑了优化单目标makespan，没有受到任务完成后处理机所消耗成本的约束，而在现实问题中，成本也是很重要的考虑因素.

3.2 Q-learning算法

Q-learning是强化学习中经典的无监督、自学习方法，在学习过程中不需要外界环境对它进行指导，依据与环境“试错”交互得到的历史经验来指导学习方向.Q-learning有五个重要组成部分：主体(Agent)、环境/状态(s)、动作(a)、奖励值(r)以及一个用于存储Q值的Q表(Q-table).在进行一次学习之前，首先将Q表初始化(一般初始化为0)，表的横向和纵向分别代表动作和状态，表中元素即为Q值，表示为Q(s,a).在每一步的学习更新过程中，Agent通过随机选择一个可行动作a从当前状态s转移到下一个状态s′，并且新的环境会反馈一个正的或者负的奖励值r给Agent用来更新Q值.Q-learning算法简化模型如图3所示.

Q-learning算法的更新公式如下：

(10)

其中：Qt(s,a)表示更新前的Q值，Qt+1(s,a)表示更新后的Q值；(0 <≤ 1)是学习率(learning rate)，表示Agent在学习过程中对未来收益的重视程度.值越小，表示Agent越重视当前已经获得的收益；反之，表示越重视远期获得的收益；(0 <≤ 1)是折扣因子(discount rate)，表示对未来奖励值的重视程度，值越小表示越重视立即奖励；反之，表示越重视未来奖励.

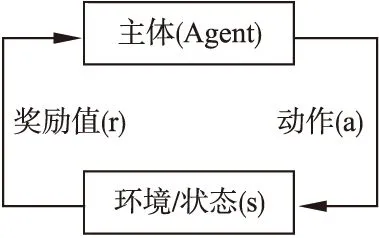
图3 Q-learning算法简化模型Fig.3 Simplified model of Q-learning algorithm

3.3 QMTS算法设计

针对所要解决的任务调度中的makespan和总成本多目标优化问题，本文将算法设计分为任务排序和虚拟机分配两个主要阶段，QMTS算法的伪代码如算法1所示.

算法1.QMTS算法

输入：DAG任务中的所有任务.

输出：makespan和总成本的结果.

初始化Q表的所有元素为0

初始化参数

计算立即奖励值r

repeatfor each episode

随机选择一个入口任务作为当前任务Tcurrent

repeatfor each step of episode

随机选择一个合法任务(不包括已经被选择过的任务)作为

下一个任务Tnext

根据式(10)更新Q(Tcurrent,Tnext)

TcurrentTnext

untilTnextisterminal

根据更新后的Q表获得任务排序

根据式(11)给每个任务分配一个虚拟机

得到makespan和总成本结果

untilconvergence(makespan和总成本的结果不再改变)

3.3.1 任务排序阶段

在本文中，使用Q-learning算法对任务进行排序，将任务视为Q-learning中的状态和动作，从当前任务到下一个任务的排序过程看作Agent在当前状态选择一个可行动作后转移到下一个状态的过程.在Q表的更新过程中，将每个任务的Upward Rank值作为该任务对应状态的立即奖励值，经过一定次数的迭代，Q表最终会收敛到固定不变.根据收敛的Q表，使用最大Q值优先原则对任务进行排序，即每次都选择符合DAG任务的依赖关系中的Q值最大的任务作为下一个执行任务，直至所有任务都完成排序过程.由于Q-learning算法在寻优问题上具有很好的学习效果，上述排序方法可以得到一个比HEFT算法更加合理的任务执行顺序，从而产生更小的makespan.

3.3.2 虚拟机分配阶段

在得到任务执行顺序之后，使用分配策略将每个任务映射到虚拟机上执行.本文将任务在每个虚拟机上的最早完成时间和虚拟机的消耗成本通过线性加权的方式进行综合考虑，每次将任务分配到加权和最小的虚拟机上执行，使得在产生更小的makespan的同时做到总成本的下降，具体公式定义如下所示：

(11)

4 实验结果与分析

4.1 实验概述及参数设置

本文中的所有实验都在云计算仿真平台WorkflowSim上进行[18].首先通过实验证明了在任务优先级排序阶段结合Q-learning算法对产生更小的makespan结果是有显著效果的，这是由于在Q-learning算法中Agent的自我学习调节过程产生了一个更好的任务执行顺序；其次，根据式(11)中权重系数的变化，分析了其对makespan和总成本两个目标的影响；再次，分别测试了在不同虚拟机数量下4种算法的性能，得到QMTS算法性能最好；最后，对不同节点数量的DAG任务进行实验，测试了QMTS算法在小任务图和大任务图上都有较好的表现，尤其是在处理规模较大的任务集时有着突出的性能优势.

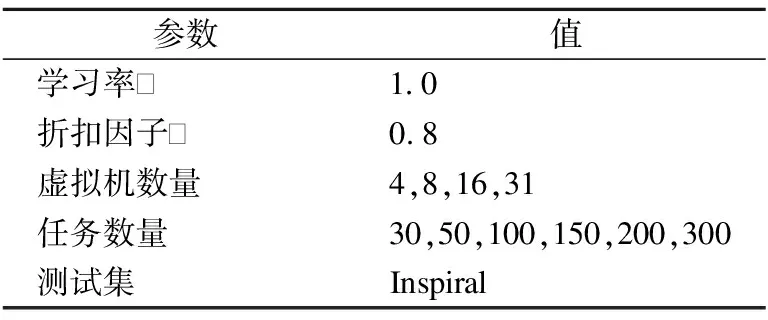
表1 实验参数设置
Table 1 Experimental parameter settings

4.2 基于Q-learning算法的任务排序实验

在云计算环境下的任务调度问题中，如何以更加合理有效的顺序将任务提交给处理机执行是调度器首先要解决的一个问题，对虚拟机最终完成任务的makespan大小起着至关重要的影响.本文使用Q-learning算法对任务进行优先级排序，并且本实验在分配任务给虚拟机时使用与HEFT算法一致的分配方式，测试了在16和32个虚拟机数量下的makespan结果，并与文献[5]中的基于Upward Rank的异构最早完成时间(Heterogeneous Earliest Finish Time based on Upward Rank，HEFT_U)算法、基于Downward Rank的异构最早完成时间(Heterogeneous Earliest Finish Time based on Downward Rank，HEFT_D)算法和处理器上的关键路径(Critical Path on a Processor，CPOP)算法进行比较.HEFT_U、HEFT_D和CPOP算法是经典并且性能较好的静态DAG任务调度算法，在优化makespan上有着较好的表现，在很多静态任务调度的研究中都被作为对比算法.

从图4的实验结果可以得知，任务集在使用了Q-learning算法对其进行执行顺序的排序后，得到了比其他3种算法更好的makespan结果，表明本文所提出的QMTS算法使用Q-learning算法对任务进行优先级排序对于减少makespan有着显著的效果.

图4 在16和32个虚拟机数量下的makespan结果Fig.4 Makespan with 16 and 32 virtual machines

4.3 权重系数实验

在对多目标优化问题进行线性加权求解时，目标函数中每个目标对象所占的权重大小情况直接影响了目标优化结果的好坏.通常情况下，当某个目标所占的权重值越大，则表示该目标越受重视，相应的目标函数会更偏向于对它的优化，并可能会直接导致其他目标产生不理想的结果.在本实验中，首先通过大量的实验，选取了在不同权重系数情况下两个目标的实验结果，权重变化对makespan和总成本的影响趋势如图5所示.

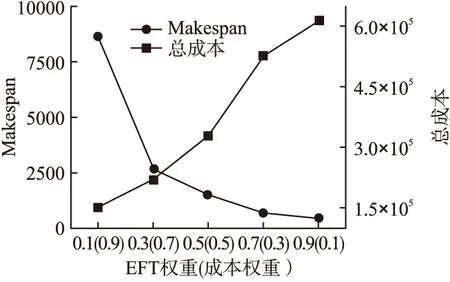
图5 权重变化对makespan和总成本的影响Fig.5 Impact of weight changes on makespan and total cost

从图5中可以得知，随着EFT的权重从小到大(成本权重由大到小)的变化，makespan产生从大到小的变化趋势，而总成本产生从小到大的变化趋势.可知，在对makespan和总成本同时进行优化时，如果对其中一个目标赋予相对过大的权重，则另一个目标会因此产生劣解，表明makespan和总成本是一对相冲突解.因此，在实验中需要选择合适的权重组合对makespan和总成本进行同时优化.在本文中，首先根据makespan和总成本结果随权重变化的大致趋势将不可能达到双目标优化目的，即会产生过差的单个目标解的权重组合剔除掉，剩下的权重组合组成一个区间，然后对这个区间内的权重组合进行大量实验，最后找到相对最优的多目标实验结果.

4.4 Inspiral_100测试集实验

本实验使用Inspiral_100测试集分别在4种不同虚拟机数量下测试了QMTS算法对makespan和总成本同时进行优化的性能，并与其它3种经典的任务调度算法进行比较.

图6(a)至图6(d)分别是在4VM、8VM、16VM、32VM情况下四种算法优化makespan和总成本的结果.图中横坐标表示4种任务调度算法，左纵坐标表示makespan结果，右纵坐标表示总成本结果.从图6可以得知，除了在32VM下，CPOP算法产生的总成本结果有略微的优势之外.在余下情况中，本文提出的QMTS算法都得到了比其他3种算法更小的makespan和总成本结果.这是因为：首先，QMTS算法在任务排序阶段使用Q-learning算法找到了一个比其他3种算法更加合理的任务执行顺序，从而产生了比其他算法更小的makespan结果；其次，又在虚拟机分配阶段综合考虑了任务最早完成时间和虚拟机执行成本两个影响因素，避免了在虚拟机分配过程中只重视对makespan的减少而忽略了对总成本消耗的控制.

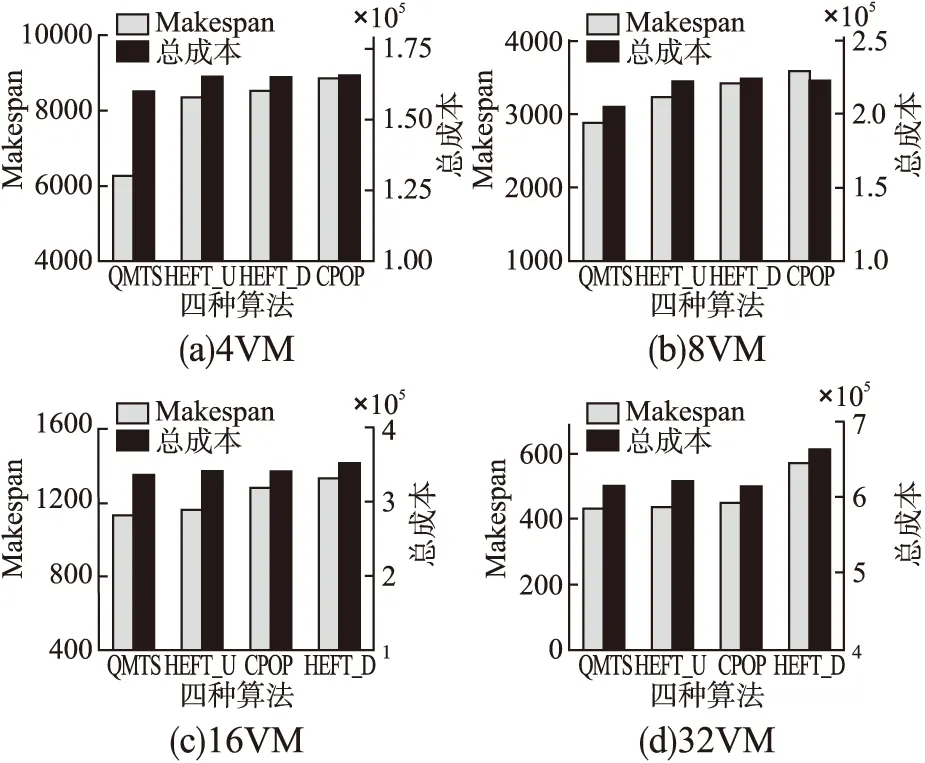
图6 不同虚拟机数量下4种算法的makespan和总成本结果Fig.6 Makespan and total cost of four algorithms under different numbers of virtual machines

4.5 Inspiral_100测试集下不同任务数量实验

最后，本文还对其他任务数量不同的Inspiral测试集在32个虚拟机环境下进行实验，表明QMTS算法在不同规模的DAG任务上的可扩展性.不同任务数量下4种算法优化makespan和总成本的结果如图7所示.

图7(a)和图7(b)分别展示了在30、50、150、200以及300个任务数量下4种算法的makespan和总成本优化结果，可以得知随着任务数量的增多，相应的makespan和总成本结果也随之增大.在30和50个任务数量下，HEFT_D算法的总成本结果相对最好，其次是QMTS算法总成本结果优于其他2种算法；但是QMTS算法的makespan结果远小于HEFT_D算法，并且和其他2种算法差不多，因此QMTS算法在小规模任务上对两个目标的优化结果是最好的.在150～300个任务的规模较大的DAG任务上，随着任务数量的增多，QMTS算法产生的makespan结果和总成本结果明显小于其他算法，说明QMTS算法随着任务数量的增多，优化性能越好.因此，本文提出的QMTS算法在不同规模的DAG任务上都能得到最好的makespan和总成本的多目标优化结果.但是由于Q-learning算法中的Q表在本文中是一个二维数组，随着任务数量和虚拟机数量的增多，相应的Q-learning中的状态s和动作a的数量也会增多，导致Q表空间增长快速，内存开销大；并且遍历整张Q表需要的时间较长，CPU计算速度随之变慢.

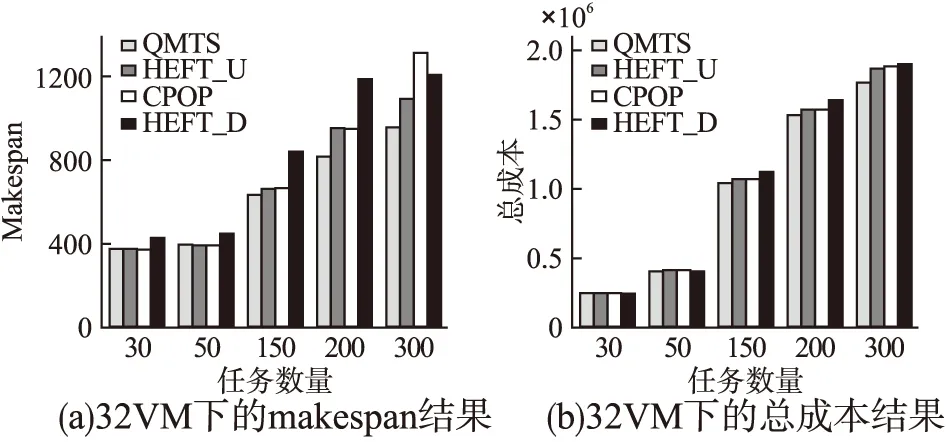
图7 不同任务数量下4种算法的makespan和总成本结果Fig.7 Makespan and total cost of four algorithms under different task numbers

5 结 语

本文针对在云计算环境下任务调度问题中的两个重要评价指标：makespan和总成本，提出同时优化这两个目标的基于Q-learning算法的静态任务调度算法QMTS.该算法首先使用Q-learning算法对任务进行优先级排序，并将HEFT算法的Upward Rank值作为Q-learning更新过程中的立即奖励值，得到一个更加合理有效的任务执行顺序；待所有任务完成排序之后，任务依次进入虚拟机分配阶段，计算任务在每个虚拟机上的最早完成时间和执行成本的线性加权和，并将任务分配给加权和最小的虚拟机执行.实验结果表明，QMTS算法在任务调度的多目标优化问题上性能有着突出的表现，说明该算法是有效的.在以后的工作中，我们将考虑使用深度神经网络拟合Q值的方法解决在Q-learning算法更新过程中Q表过大导致收敛过慢的问题；并且在优化makespan和总成本两个目标的基础上考虑对其他有重要价值意义的目标进行优化.